nLab interval object
Context
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
An interval object in a category is an object that behaves in roughly like the standard topological interval with its two boundary point inclusions
in the category Top of topological spaces, where is the copairing of the global elements and .
A bare interval object may be nothing more than such a diagram. If admits sufficiently many limits and colimits, then from this alone a lot of structure derives. The precise definition of further structure and property imposed on an interval object varies with the intended context and applications.
Notably in a large class of applications the interval object in supposed to be the right structure to ensure
-
that there is an object in such that for every object of the internal hom object exists and behaves like a path space object for ;
-
that there is a notion of composition on these path objects which induces on a structure of a (higher) category internal to : the fundamental category or fundamental groupoid of the object , or rather its fundamental infinity-groupoid.
For instance the choice Top and should be an instance of a category with interval object, and the fundamental algebraic n-groupoid obtained for any topological space from this data should be the fundamental -groupoid as a Trimble n-category.
We give two very similar definitions that differ only in some extra assumptions.
-
The first one was used by Berger and Moerdijk to generalize the Boardman–Vogt resolution of topological operads to more general operads.
-
The second is motivated from constructions appearing in the definitions of Trimble n-category and of generalized universal bundle. It includes the possibility that the interval is not weakly equivalent to the point, in which case it may be used nontrivially to test for undirected objects and probe directed objects.
Definitions
Plain definition
Definition (plain interval object)
A plain interval object in a category is just a cospan diagram with equal feet
in , with and any two objects and and any two morphisms.
In categories with finite limits it is often required that is the terminal object and in this case the interval object is called cartesian interval object.
Examples for the use of this notion is at fundamental (infinity,1)-category in the section “fundamental geometric ∞-categories”.
Contractible interval object
Definition (contractible interval object)
A contractible interval object in a category with a terminal object is an object with two global elements and such that
- for any object in and global elements and such that , there exists a morphism such that and .
Definition (contractible interval object in (n, 1)-categories)
A contractible interval object in an -category with a terminal object is an object with two global elements and and an equivalence such that
- for any object in and global elements and with an equivalence , there exists a morphism with a morphism such that the equivalences , , and satisfy the coherence laws.
The universal property of the contractible interval object means that the contractible interval object corresponds to the interval type in Martin-Löf type theory/homotopy type theory, and is thus equivalent to the terminal object. If a cartesian closed -category has an contractible interval type, the terminal object is a separator (see Mike Shulman’s blogpost).
In homotopical categories
If the ambient category is a homotopical category, such as a model category, there are natural further conditions to put on an interval object:
Trimble interval object
The following definition is strongly related to the notion of Trimble omega-category where the interval object gives the internal hom the structure of an operad giving (by induction) the model of an -category structure on
This internal -category is denoted
This is in (a bit) more detail in Trimble omega-category and in fundamental (infinity,1)-category in the section “Fundamental algebraic -categories”.
Definition (Trimble interval object)
A category with interval object is
-
a symmetric closed monoidal homotopical category ;
-
with tensor unit being the terminal object, which we write ;
-
equipped with a bi-pointed object
in , with called the interval object;
such that
Berger–Moerdijk segment- and interval object
In section 4 of
- Clemens Berger, Ieke Moerdijk, The Boardman-Vogt resolution of operads in monoidal model categories (arXiv)
the following definition is given:
Let be a monoidal model category and write for the tensor unit in (not necessarily the terminal object).
A segment (object) in a monoidal model category is
-
a factorization
of the codiagonal morphism
from the coproduct of with itself that sends each component identically to .
-
together with an associative morphsim
which has 0 as its neutral and 1 as its absorbing element, and for which is a counit.
If is equipped with the structure of a model category then a segment object is an interval in if
is a cofibration and a weak equivalence.
Interval type
In homotopy type theory the cellular interval can be axiomatized as a higher inductive type. See interval type for more.
Examples
-
In a category of chain complexes the standard interval is the simplicial chain complex on the 1-simplex, see at interval object in chain complexes.
-
The cube category is generated from a single interval object.
-
The standard interval object in Cat is the 1st oriental (see co-span co-trace)
-
For Top equipped with with the classical model structure on topological spaces, the topological closed interval (with its Euclidean metric topology) with the maps to 0 and 1, respectively. This is the standard topological interval. This is the case described in detail at Trimble n-category.
-
For the category of strict omega-categories the first oriental, the 1-globe is an interval object. In this strict case in fact all hom objects are already equal to the point and
is a strict co-category internal to Cat. In this case, for any -category the -category is just an ordinary category, namely the 1-category obtained from truncation of . Similarly, probably in this case.
Standard intervals, cubes and simplices in and
Let Top or Diff be the category of topological spaces or of manifolds.
A standard choice of interval object in is with the obvious two boundary inclusions .
But another possible choice is to let be the whole real line, but still equipped with the two maps , that hit the and , respectively.
Either of these two examples will do in the following discussion. The second choice is to be thought of as obtained from the first choice by adding “infinitely wide collars” at both boundaries of . While may seem like a more natural choice for a representative of the idea of the “standard interval”, the choice is actually more useful for many abstract nonsense constructions.
But since it is hard to draw the full real line, in the following we depict the situation for the choice .
Then for low the above construction yields this
-
– here is the point.
-
– here is just the interval itself
The two face maps and pick the boundary points in the obvious way. The unique degeneracy map maps all points of the interval to the single point of the point.
-
– here is the standard square
But the three face maps of the cosimplicial object constructed above don’t regard the full square here, but just a triangle sitting inside it, in that pictorially they identify -shaped boundaries in as follows:
(here the arrows do not depict morphisms, but the standard topological interval, i don’t know how to typeset just lines without arrow heads in this fashion!)
-
– here is the standard cube
Exercise
Insert the analog of the above discussion here and upload a nice graphics that shows the standard cube and how the cosimplicial object picks a solid tetrahedron inside it.
As a start, we can illustrate how there are 6 3-simplices sitting inside each 3-cube.
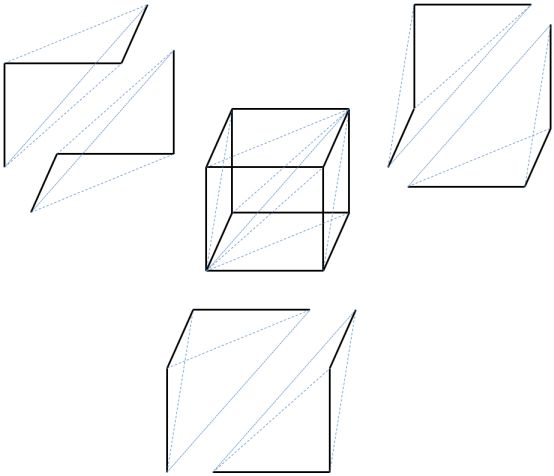
Once you see how the 3-simplices sit inside the 3-cube, the facemaps can be illustrated as follows:
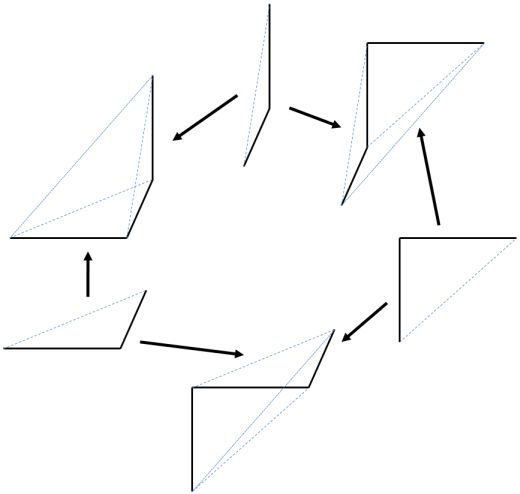
Note that these face maps are to be thought of as maps into 3-simplices sitting inside a 3-cube.
-homotopy theory
See A1-homotopy theory.
Fundamental -categories induced from intervals
The interest in interval objects is that various further structures of interest may be built up from them. In particular, since picking an interval object is like picking a notion of path, in a category with interval object there is, under mild assumptions, for each object an infinity-category – the fundamental -category of with respect to – whose k-morphisms are -fold -paths in .
This is described for two models for -categories at fundamental (infinity,1)-category
Homotopy localization induced from an interval
Given a suitable interval obect in a site , one may ask for ∞-stacks on that are invariant under the notion of homotopy induced by . These are obtained by homotopy localization of a full (∞,1)-category of (∞,1)-sheaves on .
Related concepts
References
- Clemens Berger, Ieke Moerdijk, The Boardman-Vogt resolution of operads in monoidal model categories (arXiv), section 4, p.11
Last revised on May 14, 2022 at 04:10:05. See the history of this page for a list of all contributions to it.