nLab topological interval
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Homotopy theory
homotopy theory, (∞,1)-category theory, homotopy type theory
flavors: stable, equivariant, rational, p-adic, proper, geometric, cohesive, directed…
models: topological, simplicial, localic, …
see also algebraic topology
Introductions
Definitions
Paths and cylinders
Homotopy groups
Basic facts
Theorems
Contents
Idea
Generally, a topological interval is a (bounded) interval in the real line (an open interval or a closed interval or a half-open interval or ) equipped with the subspace topology of the Euclidean metric topology.
Specifically in the context of topological homotopy theory, the standard topological interval object is the closed interval equipped with the continuous functions
which include the point space as the two endpoints, respectively.
Together with the unique function this yields the factorization of the codiagonal on the point space
which exhibits an example of an interval object in the general sense of model category theory with respect to the classical model structure on topological spaces.
Induced constructions
Topological cylinder
For a topological space, then the product topological space with the topological interval is the standard topological cylinder over . Via the above inclusion functions, this inherits a factorization of the codiagonal of (the canonical continuous function out of the disjoint union space of with itself to ):
Accordingly, with respect to the classical model structure on topological spaces this is an example a of cylinder object.
Left homotopy
Given two topological spaces and two continuous functions,then a left homotopy
is a continuous function
out of the product topological space of with the topological interval, such that this fits into a commuting diagram of the form
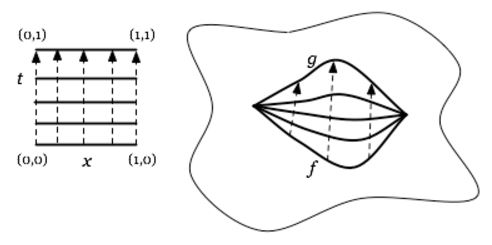
(graphics grabbed from J. Tauber here)
Path space
For a topological space, then its path space is the mapping space , out of the topological interval into , i.e. the set of continuous function equipped with the compact-open topology.
The two endpoint inclusions and the unique projection induce continuous functions
(inclusion of constant paths and endpoint evaluation of paths).
Properties
Freyd’s characterization
The topological interval may be characterized by a coalgebraic definition first identified by Freyd:
Let be the category of topological spaces equipped with a pair of distinct points, for example . Let be the functor defined on objects by
where denotes the quotient space of the disjoint union space formed by identifying the element of the first copy of with of the second copy of , where is identified with of the first copy, and is identified with of the second copy.
For there is an evident identification , and moreover there is an -coalgebra structure given by “multiplication by ”.
For more information, see coalgebra of the real interval, which shows in particular how the interval structure of may be defined by coinduction.
Last revised on August 5, 2025 at 00:57:53. See the history of this page for a list of all contributions to it.