nLab para construction

Idea

The Para construction is a variety of strictly related functorial constructions that produce a category of parametric morphisms.

In the simplest case, one starts with a monoidal category $\mathcal{C}$ and builds a category $\mathbf{Para}(\mathcal{C})$ whose morphisms $A \to B$ are pairs $(P,f)$ where $P:\mathcal{C}$ is a parameter and $f: A \otimes P \to B$ is a morphism in $\mathcal{C}$.

Such a morphism might be visualised using the graphical language of monoidal categories (below, left). However, this notation does not emphasise the special role played by $P$, which is part of the data of the morphism itself. Parameters and data in machine learning have different semantics; by separating them on two different axes, we obtain a graphical language which is more closely tied to these semantics (below, right).

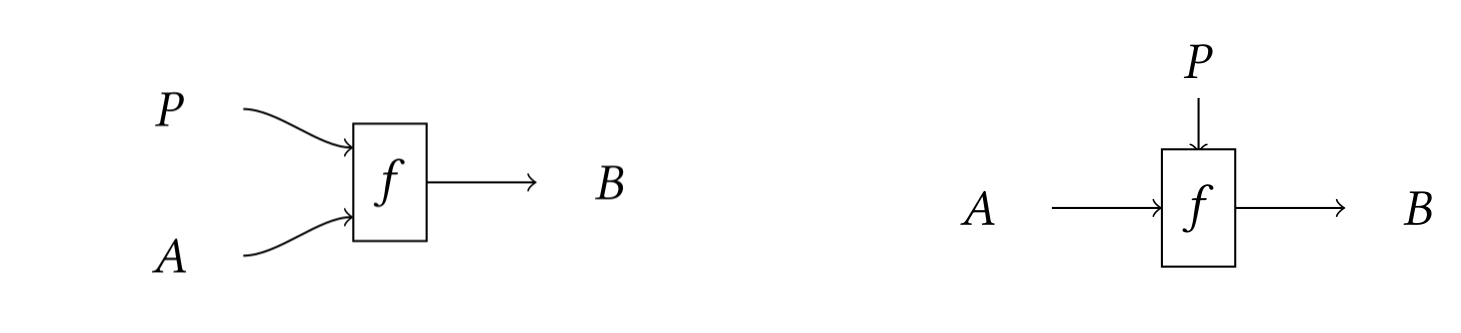
This gives us an intuitive way to compose parameterised maps:

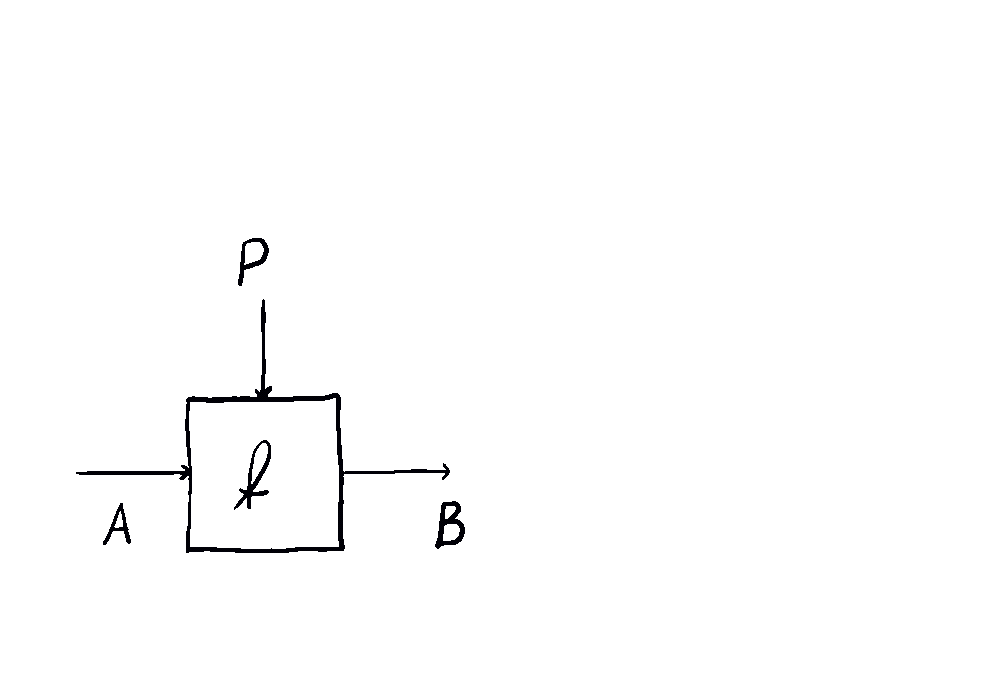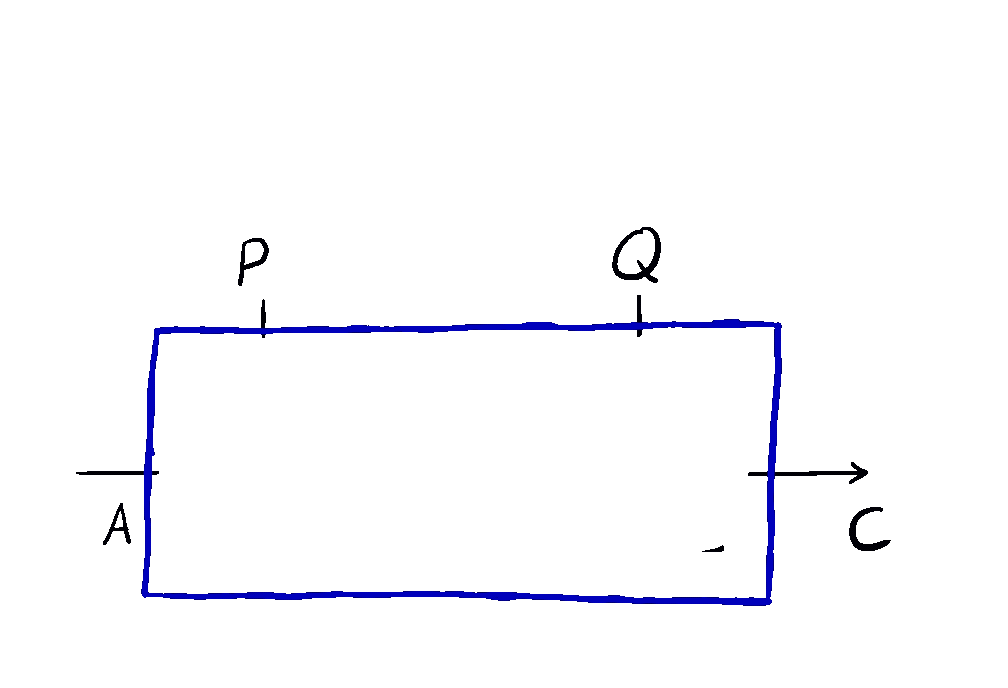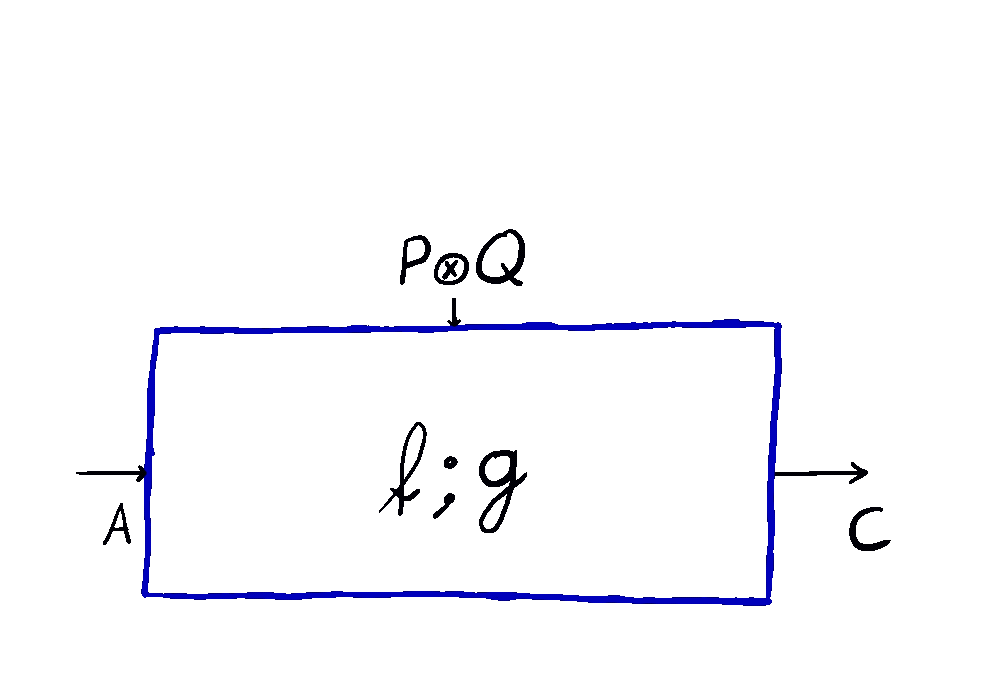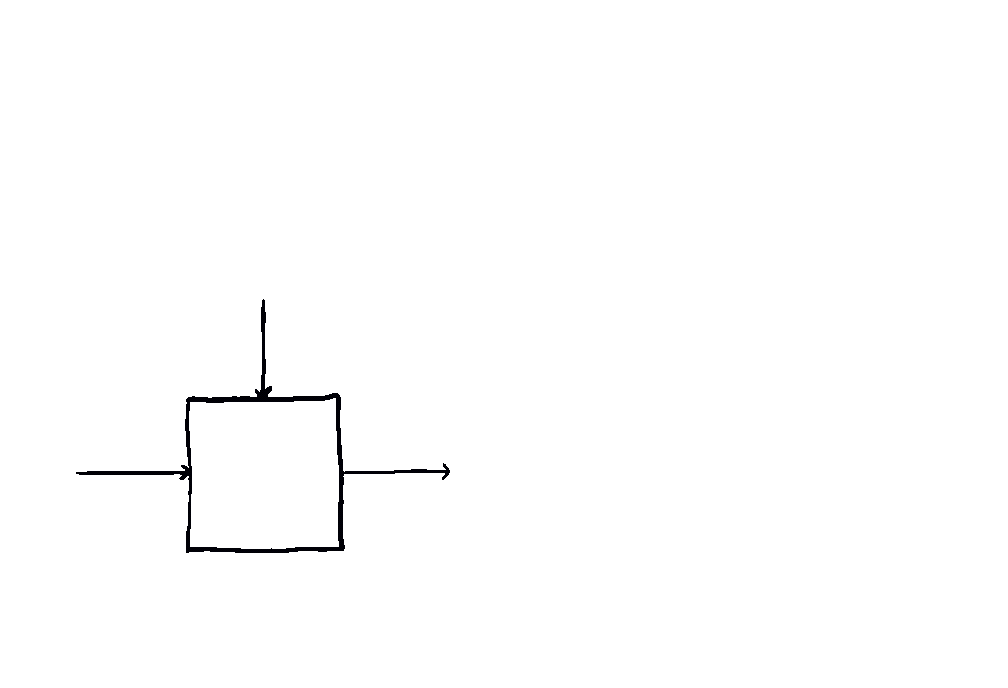
The Para construction is of relevance in categorical cybernetics, since controlled processes such as machine learning models, economic agents and Bayesian reasoners are straightforwardly modeled as parametric processes of some kind.

Indeed, the notation $\mathbf{Para}(\mathcal{C})$ was originally introduced in (Fong, Spivak and Tuyeras 2019), and then successively refined in (Gavranovic 2019) and (Cruttwell et al. 2021) for applications to machine learning. (Capucci et al. 2020) generalized the construction from monoidal categories to actegories, in order to capture examples from other areas of categorical cybernetics. A still further generalization and systematization of the Para construction is being developed by David Jaz Myers and Matteo Capucci, see (Myers 2022) and (Capucci 2023).

Nonetheless, the 1-categorical version of Para already appears e.g. in (Hermida & Tennent 2012), with precursors in (Pavlovic 1997). Also, Baković 2008, Thm. 13.2 introduces Copara (under a different name) in the very general context of actions of bicategories.

Definition

For monoidal categories

Definition

For $(\mathcal{C}, I, \otimes)$ a monoidal category, $\mathbf{Para}(\mathcal{C})$ is the bicategory given by the following data:

• Its objects are the objects of $\mathcal{C}$.

• A 1-morphism $A \to B$ is a choice of a parameter object $P \colon \mathcal{C}$ and a morphism in $\mathcal{C}$ of the form

  $$f \colon A \otimes P \to B \,.$$

• A 2-morphism $(P, f) \Rightarrow (Q, g)$ is a morphism $r \colon P \to Q$ in $\mathcal{C}$ such that the following diagram commutes:

• Identity morphisms are given by the right unitors:

  $$(I, \rho) \colon X \otimes I \xrightarrow{\rho_X} X \,.$$

• The composite of a map $f \colon A \otimes P \to B$ and $g \colon B \otimes Q \to C$ is given by the animation above. In symbols, this is the $P \otimes Q$-parameterised map defined as

  $$A \otimes P \otimes Q \xrightarrow{f \otimes Q} B \otimes Q \xrightarrow{g} C$$

• The data of associators and unitors for the bicategory, as well as their coherence diagrams, are defined using those of $\mathcal{C}$.

If $\mathbf{C}$ is strict monoidal, then $\mathbf{Para}(\mathcal{C})$ is a 2-category. One can show that if $\mathbf{C}$ is commutative, then $\mathbf{Para}(\mathcal{C})$ is symmetric monoidal, since commutativity of $\otimes$ allows one to exhibit an interchange. It is believe this still holds if $\mathbf{C}$ is just symmetric, making $\mathbf{Para}(\mathcal{C})$ a symmetric monoidal bicategory.

For actegories

Definition

Let $(\mathcal{M}, I, \otimes)$ be a monoidal category and let $(\mathcal{C}, \odot)$ be a right $\mathcal{M}$-actegory. Then $\mathbf{Para}(\odot)$ is a bicategory with the following data:

• Its 0-cells are the objects of $\mathcal{C}$.
• A 1-cell $A \to B$ is a choice of a parameter object $P : \mathcal{M}$ and a morphism
  $$f : A \odot P \to B$$

  in $\mathcal{C}$.

• A 2-cell $(P, f) \Rightarrow (Q, g)$ is a morphism $r : P \to Q$ in $\mathcal{M}$ such that the following commutes:

• Identity morphisms are given by the unitors:
  $$(I, \eta) : X \odot I \xrightarrow{\eta_X} X$$
• The composition of a map $f : A \odot P \to B$ and $g : B \odot Q \to C$ is defined as
  $$A \odot (P \otimes Q) \cong (A \odot P) \odot Q \xrightarrow{f \odot Q} B \odot Q \xrightarrow{g} C$$
• The data of associators and unitors for the bicategory, as well as their coherence diagrams, are defined using those of $\mathcal{M}$ and $\odot$.

Again, it is folklore that this bicategory is symmetric monoidal when $\odot$ is a symmetric monoidal action, meaning $\mathcal{C}$ is monoidal, $\mathcal{M}$ is symmetric and $\odot$ is a symmetric monoidal functor.

Also, this construction is 2-functorial from $\mathcal{M}\mathbf{Act}$ to $\mathbf{Bicat}$.

Dual construction: copara and bipara

Given a left $\mathcal{M}$-actegory, one can produce a bicategory of coparametric morphisms $f: A \to P \odot B$ by dualizing the above construction in the obvious way. This is known as $\mathbf{Copara}(\odot)$.

Likewise, given an $\mathcal{M}$-biactegory there is a bicategory $\mathbf{Bipara}(\odot, \odot')$ whose 1-cells are biparametric morphisms $f: A \odot P \to Q \odot B$, whose composition rule uses the bimodulator of the biactegory.

Generalizations

The Para construction naturally generalizes in five different ways (with the first four described in (Myers 2022)):

(1.) Move from bicategories to double categories (in the weak sense): $\mathbf{Para}(\mathcal{C})$ is usefully thought of as a double category whose tight category is still $\mathcal{C}$, whose loose maps are parametric morphisms, and whose squares are reparametrizations that commute suitably:

(2.) Allow for colax actions. This includes comonads (and graded comonads more generally), since they are colax actions of the terminal monoidal category; and applying Para to a comonad yields a double categorical version of the coKleisli category of the comonad.

(3.) Allow for “dependent parameters”, i.e. for situation in which the parameter $P$ of a parametric morphism $f: A \odot P \to B$ actually depends on $A$, thus allowing for $f$ of the form $f: (a:A) \times P(a) \to B$ (notation is suggestive). This makes double categories such as $\mathbf{Span}(\mathcal{C})$ instances of the Para construction (where the left leg encodes the parameter dependency and the right leg is the parametric morphism itself).

(4.) Have the construction take place in complete 2-categories, as opposed to $\mathbf{Cat}$. This allows to describe Para for structured categories and to apply it to different 2-categorical structures (e.g. indexed categories).

(5.) Internal vs. external parameterisation: given a $\mathcal{M}$-actegory $(\mathcal{C}, \odot)$, the Para construction describes parameterisation which is internal to the category $\mathcal{C}$. For instance, given an action on the category Vect, a morphism $f : A \odot P \to B$ is a linear map. But often we are interested in morphisms linear only in one variable, for instance, a function $f : \mathbf{Set}(P, \mathbf{Vect}(A, B))$. In such cases we’re interested in external parameterisation, one which is captured by $\mathcal{C}$ being an object of $\mathcal{M}Cat$, instead of $\mathcal{M}Act$. A unified perspective on these two approaches is that of a locally graded category.

In categorical cybernetics

Para has been developed to model effectively the compositional structure of controlled processes, such as those involving agents. The examples better developed are in deep learning and game theory, see (Capucci et al. 2020).

The idea that agents are parametric functions is quite old. In fact, agents take in an input $A$ and produce an output $B$. However, they have additional inputs/outputs not available to the “outside world”, i.e. not part of their composition interface. These can be the weights (or parameters) of a neural network (or a more general ML model), the strategies of a player in an economic game, the control signal of a controlled ODE or a Markov decision process.

Thus agents are naturally modelled as parametric morphisms.

Examples

• The Cayley graph of a monoid action (together with its category structure) is a low-dimensional example of a Para construction for actegories.

• When the base category is set to be the category of optics, then $\mathbf{Para(\mathbf{Optic(\mathcal{C})})}$ recovers the category of neural networks defined in (Capucci et al. 2020).

• The “monoidal indeterminates” construction of Hermida and Tennent is a Para construction for actegories. Hermida and Tennent consider a symmetric monoidal functor $j:\mathbf{\Sigma}\to \mathcal{C}$ (hence: a symmetric monoidal action of $\mathbf{\Sigma}$ on $\mathcal{C}$) and provide a symmetric monoidal bicategory $\mathcal{C}(\mathbf{x}:j)$ and ordinary monoidal category $\mathcal{C}[\mathbf{x}:j]$. The morphisms $X\to Y$ in $\mathcal{C}(\mathbf{x}:j)$ are pairs $(w,f)$ where $w$ is in $\mathbf{\Sigma}$ and $f:X\otimes j(w)\to Y$ in $\mathcal{C}$.

• If we quotient $\mathbf{Para}(\mathcal{C})$ to get a 1-category by equating connecting components of 1-cells, this is a semicocartesian monoidal category. In fact it is the semicocartesian reflection of $\mathcal{C}$. (See (Hermida and Tennent, Corollary 2.13).) Similarly, quotienting $\mathbf{CoPara}(\mathcal{C})$ gives the semicartesian reflection of $\mathcal{C}$.

• In particular, if we start from the category $\mathbf{FdIsometry}$ of finite dimensional Hilbert spaces and isometries, the 1-cells of $\mathbf{CoPara}(\mathbf{FdIsometry})$ are Stinespring dilations of quantum channels, and the quotiented 1-category is equivalent to the category of quantum channels (see (Huot and Staton 2018)).

Related concepts

• action of a monoidal category
• lens (in computer science)

References

The Para construction first appears (though not under that name) in:

• Claudio Hermida, Robert Tennent. Monoidal indeterminates and categories of possible worlds. Theoretical Computer Science vol 430. 2012. Preliminary version in MFPS 2009. doi:j.tcs.2012.01.001

• Duško Pavlović, Categorical logic of names and abstraction in action calculi. Math. Structures Comput. Sci. 7 (6) (1997) 619–637. pdf

• Igor Baković, Bigroupoid 2-torsors. Dissertation, LMU München: Faculty of Mathematics, Computer Science and Statistics, (pdf)

The terminology “Para construction” first appears in:

• Brendan Fong, David Spivak, Rémy Tuyéras, Backprop as Functor: A compositional perspective on supervised learning, 34th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS) 2019, pp. 1-13, 2019. (arXiv:1711.10455, LICS’19)

It has then be developed for the purposes of machine learning in:

• Bruno Gavranović, Compositional Deep Learning [arXiv:1907.08292]

• G.S.H. Cruttwell, Bruno Gavranović, Neil Ghani, Paul Wilson, Fabio Zanasi, Categorical Foundations of Gradient-Based Learning, (arXiv:2103.01931)

• G.S.H. Cruttwell, Bruno Gavranović, Neil Ghani, Paul Wilson, Fabio Zanasi, Deep Learning for Parametric Lenses, (arXiv:2404.00408)

and generalized further to actegories for the purposes of categorical cybernetics in:

• Matteo Capucci, Bruno Gavranović, Jules Hedges, Eigil Fjeldgren Rischel, Towards Foundations of Categorical Cybernetics, (arXiv:2015.06332)

The generalization of the Para construction being developed by David Jaz Myers and Matteo Capucci is expounded in the following talks:

• David Jaz Myers, The Para construction as a distributive law, talk at the Virtual Double Categories Workshop (2022) [slides, video]

• Matteo Capucci, Constructing triple categories of cybernetic processes [slides, video]

• Matteo Capucci, Para Construction as a Wreath Product, talk at CQTS (Jan 2024) [slides: pdf]

A view on quantum channels via CoPara:

• Mathieu Huot, Sam Staton, Universal properties in quantum theory (QPL 2018) (pdf).