nLab Center for Quantum and Topological Systems
The Center for Quantum and Topological Systems (CQTS, launched in 2021) is a research center within the Research Institute of New York University in Abu Dhabi.
CQTS is concerned with fundamental questions of quantum systems relevant for quantum technologies — quantum materials, quantum information, quantum sensing, quantum computing, quantum algorithms — with a hallmark focus on foundations of the oft neglected but long-term necessary aspect of topological stabilization via hardware based on topologically ordered phases of quantum materials.
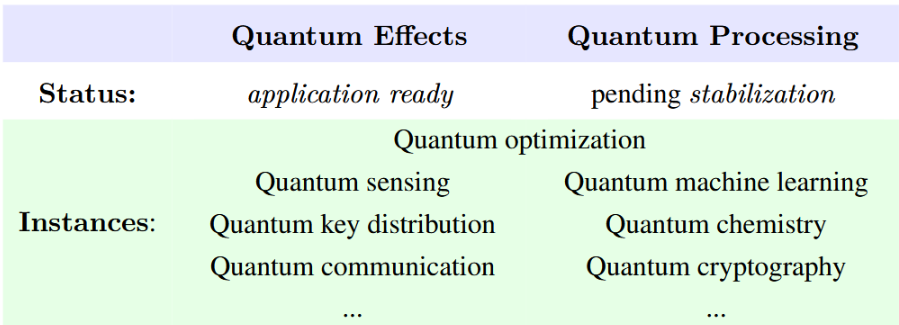
To this end, the theory heart of the center develops understanding of otherwise elusive strongly cloupled/correlated condensed matter (such as fractional quantum Hall systems) via “geometric engineering on branes” [SS25a], alongside a compatible development of topology-aware quantum programming languages [SS25b, SS25c] based on insights from stable homotopy theory – an approach informed by high energy physics and algebraic topology. At the same time, the center’s Quantum Labs develop spin-based cold atom platforms for quantum sensing [Eq22] and related quantum technologies (such as quantum key distribution) that do not require further stabilization and hence are near-term application ready.
The following lists the center’s public activities, notably local events and local weekly seminars, international and regional events, with further materials (slides, references, videos) provided where available.

Contents
- Conferences & Workshops
- Jun 2022
- Jan 2023
- Feb 2023
- Mar 2023
- Apr 2023
- May 2023
- Oct 2023
- Jan 2024
- Apr 2024
- May 2024
- Oct 2024
- Nov 2024
- Dec 2024
- Jan 2025
- Feb 2025
- Apr 2025
- May 2025
- Quantum Colloquium
- May 2022
- Sep 2022
- Oct 2022
- Nov 2022
- Dec 2022
- Jan 2023
- Feb 2023
- Mar 2023
- Apr 2023
- May 2023
- Sep 2023
- Oct 2023
- Nov 2023
- Dec 2023
- Jan 2024
- Feb 2024
- Mar 2024
- Apr 2024
- May 2024
- Sep 2024
- Oct 2024
- Nov 2024
- Dec 2024
- Jan 2025
- Feb 2025
- Apr 2025
- May 2025
- Geometry, Topology & Physics (GTP) Seminar
- Feb 2022
- Mar 2022
- Apr 2022
- May 2022
- Sep 2022
- Oct 2022
- Nov 2022
- Dec 2022
- Jan 2023
- Feb 2023
- Mar 2023
- Apr 2023
- May 2023
- Sep 2023
- Oct 2023
- Nov 2023
- Dec 2023
- Jan 2024
- Feb 2024
- Mar 2024
- Apr 2024
- May 2024
- Sep 2024
- Oct 2024
- Nov 2024
- Dec 2024
- Feb 2025
- Mar 2025
- Apr 2025
- May 2025
- External presentations
Conferences & Workshops
Jun 2022
Homotopical perspectives on Topological data analysis
Organizers: Sadok Kallel and Hisham Sati

Schedule for 02 June 2022:
-
15:00 - 16:00 GST/UTC+4
Ling Zhou (The Ohio State University, USA)
Persistent homotopy groups of metric spaces
By capturing both geometric and topological features of datasets, persistent homology has shown its promise in applications. Motivated by the fact that homotopy in general contains more information than homology, we study notions of persistent homotopy groups of compact metric spaces, together with their stability properties in the Gromov-Hausdorff sense. Under fairly mild assumptions on the spaces, we proved that the classical fundamental group has an underlying tree-like structure (i.e. a dendrogram) and an associated ultrametric. We then exhibit pairs of filtrations that are confounded by persistent homology but are distinguished by their persistent homotopy groups. We finally describe the notion of persistent rational homotopy groups, which is easier to handle but still contains extra information compared to persistent homology.
-
16:00 - 17:00 GST/UTC+4
Wojciech Chacholski (KTH, Sweden)
Realisations of Posets
My presentation is based on an article with the same title coauthored with A. Jin and F. Tombari (arXiv:2112.12209).
Encoding information in form of functors indexed by the poset of -tuples of real numbers (persistence modules) is attractive for three reasons:
a) metric properties of the poset are essential to study distances on persistence modules
b) the poset of -tuples of real numbers has well behaved discrete approximations which are used to provide finite approximations of persistence modules
c) the mentioned discretizations and approximations have well studied algebraic and homological properties as they can be identified with multi graded modules over polynomial rings.
In my talk I will describe a construction called realisation, that transforms arbitrary posets into posets which satisfy all three requirements above and hence are particularly suitable for persistence methods.Intuitively the realisation associates a continuous structure to a locally discrete poset by filling in empty spaces. For example the realisation of the poset of natural numbers is the poset of non-negative reals. I will focus on illustrating how homological techniques, such as Koszul complexes, can be used to study persistence modules indexed by realisations.
-
17:30 - 18:30 GST/UTC+4
Grégory Ginot (Université Paris 13, France)
Homotopical and sheaf theoretic point of view on multi-parameter persistence.
In this talk we will highlight the study of level set persistence through the prism of sheaf theory and a special type of 2-parameter persistence: Mayer-Vietoris systems and a pseudo-symetry between those. This is based on joint work with Berkouk and Oudot.
-
18:30 - 19:30 GST/UTC+4
Rick Jardine (University of Western Ontario, Canada)
Thoughts on big data sets
This talk describes work in progress. The idea is to develop methods for analyzing a very large data sets in high dimensional spaces. There are well-known pitfalls to avoid, including the inability to computationally analyze TDA constructions for on account of its size, the “curse of high dimensionality”, and the failure of excision for standard TDA constructions. We discuss the curse of high dimensionality and define a hypercube metric on that may lessen its effects. The excision problem for the Vietoris-Rips construction can be addressed by expanding the TDA discussion to filtered subobjects of Vietoris-Rips constructions. Unions of such subobjects satisfy excision in path components (clusters) and homology groups, by classical results. The near-term goal is to construct, for each data point , a “computable” filtered subcomplex with , which would capture spatial local behaviour of the data set near . A large (but highly parallelizable) algorithm finds a nearest neighbour, or a set of -nearest neighbours for a fixed data point . Some variant of this algorithm may lead to a good construction of the local subcomplex .
Jan 2023
-
12-15 Jan 2023
M-Theory and Mathematics 2023 – Classical and Quantum Aspects
on M-theory (non-perturbative string theory and related quantum field theories)

[logo adapted from JMP 62 (2021) 042301]
Feb 2023
24 Feb 2023
CQTS and TII Workshop 2023
joint workshop with the Quantum Research Center (QRC) at the Technology Innovation Institute (TII) in Abu Dhabi
on quantum materials, quantum computation and quantum programming

-
9:00 - 9:05
Welcome
-
9:05 - 9:15
Introduction to Quantum Physics @ TII
-
9:20 - 9:45
-
9:50 - 10:10
Coherence of confined matter in lattice gauge theories at the mesoscopic scale
-
10:15 - 10:40
Break: 10:40 - 11:10
-
11:10 - 11:15
Intro to Quantum Algorithms @TII
-
11:20 - 11:50
-
11:55 - 12:25
Egor Tiunov:
Quantum-inspired algorithms
-
12:30 - 13:00
Thais de Lima Silva:
Quantum algorithms: Quantum Signal Processing
Lunch: 13:00 – 2:15
-
14:15 - 14:25
Introducing research and researchers @CQTS
-
14:30 - 14:50
Quantum information processing via NLS
-
15:00 - 15:20
Tuning topological quantum materials
-
15:30 - 15:50
Verified quantum programming with linear HoTT
Break: 3:50-4:20 pm
-
4:20 - 4:40
Topological Quantum field theory for TQC
-
16:50 - 17:10
Topological Qubits from Anyons
-
17:20 - 17:50
Towards verified hardware-aware topological quantum programming
Mar 2023
15-18 Mar 2023
Geometric/Topological Quantum Field Theories and Cobordisms (webpage)
on functorial quantum field theory, knot homology and cobordism theory/cobordism categories/cobordism hypothesis

[logo adapted from arXiv:2103.01877]

Mee Seong Im, Mikhail Khovanov, Vivek Singh, Sergei Gukov, Anna Beliakova, Khaled Qazaqzeh
Domenico Fiorenza, Carlo Collari, Sadok Kallel, Nafaa Chbili, Christian Blanchet, David Jaz Myers
Nitu Kitchloo, Daniel Berwick-Evans, Adrian Clough
Sachin Valera, Alonso Perez-Lona, Urs Schreiber Daniel Grady, Christoph Schweigert
Hisham Sati, Konrad Waldorf, Dmitri Pavlov
-
Mikhail Khovanov (Columbia University):
Universal construction, foams and link homology
cf.: arXiv:1808.09662, arXiv:2011.11077
In this series of three talks we will explain the foam approach to link homology. Bigraded link homology theories categorify the Jones polynomial and other Reshetikhin-Turaev link invariants, such as the HOMFLY-PT polynomial. Foams, which are polyhedral 2D complexes embedded in 3-space allow to construct state spaces for planar graphs which are then used to define link homology groups. The most explicit and efficient way to define graph state spaces is via evaluation of the closed foams (Robert-Wagner formula).
A) This formula will be first explained in the less technical unoriented case. Resulting graph state spaces are then related to the Four-Color Theorem and Kronheimer-Mrowka homology for 3-orbifolds.
B) A step in that construction requires building a topological theory (a lax TQFT) from an evaluation of closed objects, such as closed -manifolds. We will explain the setup for topological theories, including in two dimensions, recovering the Deligne categories and their generalizations. In one dimension and adding defects, these topological theories are related to noncommutative power series, pseudocharacters, and, over the Boolean semiring, to regular languages and automata.
C) Robert-Wagner foam evaluation and its application to constructing link homology theories will be explained as well.
-
Nitu Kitchloo (John Hopkins University):
Symmetry breaking and homotopy types for link homologies
cf.: arXiv:1910.07443, arXiv:1910.07444, arXiv:1910.07516
video: YT
I will describe how the spaces that record symmetry breaking data in a -gauge theory (for arbitrary ) can be used to construct homotopy types that are invariants for links in . In particular, I will show how one may recover Khovanov-Rozansky link homology and link homology by evaluating this homotopy type under suitable cohomology theories.
-
Sergei Gukov (DIAS, Dublin and Caltech)
Machine learning and hard problems in topology
cf.: arXiv:2010.16263
slides: pdf
video: YT
-
Nils Carqueville (University of Vienna):
Truncated Rozansky-Witten models as extended defect TQFTs
cf.: arXiv:2201.03284
video: YT
According to the cobordism hypothesis with singularities, fully extended topological quantum field theories with defects are equivalently described in terms of coherent full duality data for objects and (higher) morphisms as well as appropriate homotopy fixed point structures. We discuss the 2-dimensional oriented case in some detail and apply it to truncated affine Rozansky-Witten models, which are under very explicit computational control. This is joint work with Ilka Brunner, Pantelis Fragkos, and Daniel Roggenkamp.
-
Arun Debray (Purdue University):
Twisted string bordism and a potential anomaly in heterotic string theory
cf.: arXiv:2210.04911
video: YT
Quantum field theories can have an inconsistency called an anomaly, formulated as an invertible field theory in one dimension higher. Theorems of Freed-Hopkins-Teleman and Freed-Hopkins classify invertible field theories in terms of bordism groups. In this talk, I’ll apply this to the low-energy approximation of heterotic string theory; Witten proved anomaly cancellation in a restricted setting, but we perform a twisted string bordism computation to show that the relevant group of 11-dimensional invertible field theories does not vanish, and therefore there could be an anomaly in heterotic string theory. Standard computational techniques for twisted string bordism do not work for this problem; I will also discuss work joint with Matthew Yu using Baker-Lazarev’s R-module Adams spectral sequence to simplify a large class of twisted spin and string bordism computations.
-
Matthew Young (Utah State University):
Non-semisimple TFT and Chern-Simons theory
cf.: arXiv:2210.04286 and super Chern-Simons theory
slides: pdf
video: YT
Chern-Simons theory, as introduced by Witten, is a three dimensional quantum gauge theory associated to a compact simple Lie group and a level. The mathematical model of this theory as a topological field theory was introduced by Reshetikhin and Turaev and is at the core of modern quantum topology. The goal of this talk is to explain a non-semisimple modification of the construction of Reshetikhin and Turaev which realizes Chern-Simons theory with gauge supergroup , as studied in the physics literature by Rozansky-Saleur and Mikhaylov. The key new algebraic structure is a relative modular structure on the category of representations of the quantum group of . Based on joint work with Nathan Geer.
-
Mee Seong Im (United States Naval Academy):
Correspondence between automata and one-dimensional Boolean topological theories and TQFTs
cf.: arXiv:2301.00700
video: YT
Automata are important objects in theoretical computer science. I will describe how automata emerge from topological theories and TQFTs in dimension one and carrying defects. Conversely, given an automaton, there’s a canonical Boolean TQFT associated with it. In those topological theories, one encounters pairs of a regular language and a circular regular language that describe the theory.
-
Alexander Schenkel (University of Nottingham):
Quantum field theories on Lorentzian manifolds
cf.: arXiv:2208.04344 and homotopical AQFT
slides: pdf
video: YT
This talk provides an introduction and survey of recent developments in algebraic QFT on Lorentzian manifolds. I will outline an axiomatization of such QFTs in terms of operad theory and illustrate this formalism through classification results in low dimensions. One of the central axioms is a certain local constancy condition, called the time-slice axiom, that encodes a concept of time evolution. Using model categorical localization techniques, I will show that this i.g. homotopy-coherent time evolution admits a strictification in many relevant cases. I will conclude this talk by explaining similarities and differences between algebraic QFT and other approaches such as factorization algebras and functorial field theories.
-
Konrad Waldorf (University of Greifswald):
The stringor bundle
cf.: arXiv:2206.09797
video: YT
The stringor bundle plays the role of the spinor bundle, but in string theory instead of quantum mechanics. It has been anticipated in pioneering work of Stolz and Teichner as a vector bundle on loop space. I will talk about joint work with Matthias Ludewig and Peter Kristel that provides a fully rigorous and neat presentation of the stringor bundle as an associated 2-vector bundle, via a representation of the string 2-group on a von Neumann algebra.
-
Domenico Fiorenza (Sapienza University of Rome):
String bordism invariants in dimension 3 from -valued TQFTs
cf.: arXiv:2209.12933
pdf: pdf
video: YT
The third string bordism group is known to be 24. Using Waldorf’s notion of a geometric string structure on a manifold, Bunke-Naumann and Redden have exhibited integral formulas involving the Chern-Weil form representative of the first Pontryagin class and the canonical 3-form of a geometric string structure that realize the isomorphism between the third string bordism group and (these formulas have been recently rediscovered by Gaiotto, Johnson-Freyd & Witten). In the talk I will show how these formulas naturally emerge when one considers the -valued 3d TQFTs associated with the classifying stacks of Spin bundles with connection and of String bundles with geometric structure. Joint work with Eugenio Landi (arXiv:2209.12933).
-
Christian Blanchet (Université Paris Cité):
Heisenberg homologies of surface configurations
cf.: arXiv:2306.08614, arXiv:2206.11475
slides: pdf
video: YT
The Heisenberg group of a surface is the central extension of its one-dimensional homology associated with the intersection cocycle. We show that a representation of the Heisenberg group defines local coefficients on the unordered configuration space of points in the surface. We study the corresponding homologies, the Mapping Class Group action and the connection with quantum constructions. This is based on joint work with Awais Shaukat and Martin Palmer.
-
Nafaa Chbili (United Arab Emirates University):
Quasi-alternating links, Examples and obstructions
cf.: arXiv:2009.08624
video: YT
Quasi-alternating links represent an important class of links that has been introduced by Ozsváth and Szabó while studying the Heegaard Floer homology of the branched double-covers of alternating links. This new class of links, which share many homological properties with alternating links, is defined in a recursive way which is not easy to use in order to determine whether a given link is quasi-alternating. In this talk, we shall review the main obstruction criteria for quasi-alternating links. We also discuss how new examples of quasi-alternating links can constructed.
-
Khaled Qazaqzeh (Kuwait University):
On the Finiteness of Quasi-alternating Links
cf.: arXiv:2208.02984
slides: pdf
video: YT
The generalization of alternating links to quasi-alternating links raises some natural questions that have affirmative answer in the class of alternating links.
In this talk, we discuss these questions and then we give an affirmative answer to one question without any assumption. As a consequence, we prove that one of these questions is solved in the affirmative iff Green’s conjecture on the finiteness of quasi-alternating links of a given determinant holds. Also, we prove that another question is solved in the affirmative implies Green’s conjecture on the finiteness of quasi-alternating links of a given determinant holds.
-
Dmitri Pavlov (Texas Tech University):
The geometric cobordism hypothesis
cf.: arXiv:2011.01208, arXiv:2111.01095
video: YT
I will explain my recent joint work with Daniel Grady on locality of functorial field theories (arXiv:2011.01208) and the geometric cobordism hypothesis (arXiv:2111.01095). The latter generalizes the Baez–Dolan cobordism hypothesis to non-topological field theories, in which bordisms can be equipped with geometric structures, such as smooth maps to a fixed target manifold, Riemannian metrics, conformal structures, principal bundles with connection, or geometric string structures. Applications include a generalization of the Galatius–Madsen–Tillmann–Weiss theorem, a solution to a conjecture of Stolz and Teichner on representability of concordance classes of functorial field theories, and a construction of power operations on the level of field theories (extending the recent work of Barthel-Berwick-Evans-Stapleton).
I will illustrate the general theory by constructing the prequantum Chern-Simons theory as a fully extended nontopological functorial field theory.
If time permits, I will discuss the ongoing work on defining quantization of field theories in the setting of the geometric cobordism hypothesis.
-
Daniel Grady (Wichita State University):
Deformation classes of invertible field theories and the Freed-Hopkins conjecture
slides: pdf
video: YT
In their seminal paper, Freed and Hopkins proved a classification theorem that identifies deformation classes of certain invertible topological field theories with the torsion subgroup of some generalized cohomology of a Thom spectrum. They conjectured that the identification continues to hold for non-topological field theories, if one passes from the torsion subgroup to the full generalized cohomology group of the Thom spectrum. In this talk, I will discuss a result which provides an affirmative answer to this conjecture. The method of proof uses recent joint work with Dmitri Pavlov on the geometric cobordism hypothesis.
-
Daniel Berwick-Evans (University of Illinois Urbana-Champaign)
How do field theories detect the torsion in topological modular forms?
cf.: arXiv:2303.09138
video: YT
Since the mid 1980s, there have been hints of a deep connection between 2-dimensional field theories and elliptic cohomology. This lead to Stolz and Teichner's conjectured geometric model for the universal elliptic cohomology theory of topological modular forms (TMF) in which cocycles are 2-dimensional supersymmetric field theories. Basic properties of these field theories lead to expected integrality and modularity properties, but the abundant torsion in TMF has always been mysterious. In this talk, I will describe deformation invariants of 2-dimensional field theories that realize certain torsion classes in TMF. This leads to a description of the generator of in terms of the supersymmetric sigma model with target .
-
Christoph Schweigert (Hamburg University)
String-net methods for CFT correlators
cf.: arXiv:2302.01468
slides: pdf
video: YT
Based on a graphical calculus for pivotal bicategories, we develop a string-net construction of a modular functor. We show that a rigid separable Frobenius functor between strictly pivotal bicategories induces a linear map between the corresponding bicategorical string-net spaces that is compatible with the mapping class group actions and with sewing. This result implies that correlators of two-dimensional conformal field theories factorize over string-net spaces constructed from defect data.
-
Anna Beliakova (University of Zurich):
On algebraisation of low-dimensional Topology
cf.: arXiv:2205.11385
video: YT
Categories of -cobordisms (for , and ) are among the most studied objects in low dimensional topology. For we know that is a monoidal category freely generated by its commutsative Frobenius algebra object: the circle. This result also classifies all TQFT functors on . In this talk I will present similar classification results for special categories of 3- and 4-cobordisms. They were obtained in collaboration with Marco De Renzi and are based on the work of Bobtcheva and Piergallini. Frobenius algebra in these cases will be replaced by a braided Hopf algebra.
I plan to finish by relating our results with the famous problem in combinatorial group theory — the Andrews–Curtis conjecture.
-
Carlo Collari (University of Pisa):
Weight systems which are quantum states
cf. arXiv:2210.05399
slides: pdf
video: YT
Roughly speaking, a weight system is a function from a space of chord diagrams to the complex numbers. Weight systems can be used to recover invariants for the relevant kind of knotted object (eg. knots, links, braids etc.) from the Kontsevich integral. The work of Sati and Schreiber highlighted the connection between (horizontal) chord diagrams and higher observables in quantum brane physics. This motivates the question: “which weight systems are quantum states?” Corfield, Sati and Schreiber showed that all weight systems associated to the defining representation are indeed quantum states. In this talk I will present an extension of their result to more general weight systems.
The plan of the talk is the following; first, I will introduce the mathematical problem. Then, I will review the proof given by Corfield, Sati and Schreiber that weight systems associated to the defining representation are quantum states. Finally, I will show how this result can be extended to weight systems associated to exterior and symmetric powers of the defining representation.
-
Ralph Blumenhagen (Max-Planck-Institute for Physics, Munich):
Nullifying Cobordism in Quantum Gravity
cf.: arXiv:2208.01656, arXiv:2303.03423
slides: pdf
video: YT
In the swampland program one tries to delineate effective theories consistent with quantum gravity from those which are not by so-called swampland conjecture. As a consequence of the absence of global symmetries in QG, one such conjecture is saying that the cobordism group has to vanish. In mathematics very often these groups do not vanish right away. Physics tells us that this can be ameliorated by either gauging or breaking of the corresponding global symmetries.
First, we show how the gauging fits into some known constraints in string theory, the so-called tadpole cancellation conditions. Mathematically, this is reflecting a well-known connection between certain K-theory and cobordism groups. Second, we report on new results related to the breaking of a global symmetry via codimension one defects. In fact, going beyond topology a very similar mechanism arises for (for a long time puzzling) rolling solutions in string theory, giving rise to the notion of a dynamical cobordism conjecture.
-
Hisham Sati (CQTS, NYU Abu Dhabi):
Cobordism in Quantum M-Theory 1: M/F-Theory as Mf-Theory
In the quest for mathematical foundations of M-theory, the “Hypothesis H” that fluxes are quantized in Cohomotopy theory, implies that M-brane charges on flat spacetimes locally organize into equivariant homotopy groups of spheres. This leads generally to a correspondence between phenomena conjectured in M-theory and fundamental mathematical concepts/results in stable homotopy, generalized cohomology and Cobordism theory . (Based on arxiv.org/abs/2103.01877).
-
Cobordism in Quantum M-Theory 2: Topological Quantum Gates in HoTT
cf.: arXiv:2303.02382
video: YT
Recent results on defect branes in string/M-theory and on their holographically dual anyonic defects in condensed matter theory allow for the specification of realistic topological quantum gates, operating by anyon defect braiding in topologically ordered quantum materials. This has a surprisingly slick formulation in parameterized point-set topology, which is so fundamental that it lends itself to certification in modern homotopically typed programming languages, such as cubical Agda. (Based on arxiv.org/abs/2303.02382).
Apr 2023
-
27 Apr - 1 Mar 2023
NYUAD Hackaton on Quantum Computing 2023

May 2023
22 - 26 May 2023
Quantum Information and Quantum Matter
on quantum information, quantum matter
nyuad.nyu.edu/en/events/2023/may/quantum-information-quantum-matter.html

-
Luigi Amico, (Technology Innovation Institute, Abu Dhabi):
Coherence of confined matter in lattice gauge theories at the mesoscopic scales
Atomtronics is the emerging quantum technology of matter-wave circuits which coherently guide propagating ultra-cold atoms. The field benefits from the remarkable progress in micro optics, allowing to control the coherent matter with enhanced flexibility on the micron spatial scale. This way, both fundamental studies in quantum science and technological applications can be carried out. I will sketch recent progress in matter-wave circuitry and atomtronics-based quantum technology. In particular, I will focus on a specific scheme simulating lattice gauge theories and analyze confined matter at the mesoscopic spatial scale.
-
Tim Byrnes (NYU Shanghai):
Measurement based imaginary time evolution
cf. arXiv:2210.06923
-
Herbert Schoeller (RWTH Aachen):
Supersymmetry protected topological states and realization of periodic Witten models in two dimensional second-order topological insulators
cf.: arXiv:2212.01307
For a generic two-dimensional topological insulator with band inversion and spin-orbit coupling, we propose the generation of topological zero-energy bound states via the application of an in-plane Zeeman field breaking rotational invariance. The Zeeman field induces a surface gap and generates the topological states via a second-order mechanism generically at the surface positions where the normal component of the Zeeman field vanishes. Via the application of an additional half-integer Aharonov-Bohm flux through a hole of the system, we show that the topological states are protected by supersymmetry. For smooth surfaces, we derive an effective surface Hamiltonian in the form of a periodic Witten model and propose how the surface bound states of the supersymmetric spectrum can be calculated via a trapping mechanism in effective surface potentials. We study the whole phase diagram of the model together with its stability and discuss the high tunability of the topological states.
-
Adrien Bouhon (Cambridge University):
Non-abelian and Euler multi-gap topologies in crystalline materials
slides: pdf
-
Markus Müller (RWTH Aachen University and Forschungszentrum Jülich, Germany):
Fault-Tolerant Topological Quantum Computing: From Concepts to Experiments
To date, the construction of scalable fault-tolerant quantum computers remains a fundamental scientific and technological challenge, due to the influence of unavoidable noise. In my talk, I will first introduce basic concepts of topological quantum error correction codes, which allow one to protect quantum information during storage and processing. I will discuss recent theory work, perspectives and recent collaborative experimental breakthroughs towards fault-tolerant quantum error correction on various physical quantum computing platforms. This includes the first realisation of repeated high-performance quantum error-correction cycles on a topological surface code with superconducting qubits [1], and the first demonstration of a universal and fault-tolerant logical gate set with trapped ions [2]. Furthermore, I will present new fundamental connections between topological quantum error correction and classical statistical mechanics models, in the context of the correction of qubit loss [3,4] and the determination of fundamental error thresholds for circuit noise [5].
References
[1] S. Krinner et al., Realizing repeated quantum error correction in a distance-three surface code, Nature 605, 669 (2022)
[2] L. Postler et al., Demonstration of fault-tolerant universal quantum gate operations, Nature 605, 675 (2022)
[3] D. Vodola, et al., Twins Percolation
[4] R. Stricker et al., Deterministic correction of qubit loss, Nature 585, 207 (2020)
[5] D. Vodola et al., Fundamental thresholds of realistic quantum error correction circuits from classical spin models, Quantum 6, 618 (2022)
- (…)
Oct 2023
20 Oct 2023
Workshop on Homotopy Theory and Applications


-
The Homotopy Type of Graph Configuration Spaces
on configuration spaces of points
slides: pdf
video: YT
-
Homotopy Manifolds and Tangent Bundles in HoTT
on homotopy types of smooth manifolds in homotopy type theory
video: YT
cf. upcoming preprint
-
Model Structures for Double Categories
video: YT
-
The Homotopy Theory of Differentiable Sheaves
on the homotopy theory of smooth -groupoids
video: YT
cf. arXiv:2309.01757
-
2-Representations and 2-Vector Bundles
cf. arXiv:2208.10042
-
Higher Topos Theory in Physics
on higher topos theory in mathematical physics
video: YT
cf.: arXiv:2311.11026
Jan 2024

on January 15 - 17, 2024
at CQTS @ New York University, Abu Dhabi
Speakers:

AlfonsiGiotop. Malek Saemann Minasian Lambert Hull Schreiber He Sati X Han Tan Singh Shahbazi Myers Hohm
Talks:
Talks:
-
15 Jan 2024
Non-Relativistic M2-Branes and AdS/CFT
slides: pdf
video: kt
cf.: arXiv:2401.14955
We discuss a peculiar limit of M2-branes that leads to a non-relativistic Chern-Simons-matter theory with an infinite dimensional spacetime symmetry group and whose dynamics leads to quantum mechanics on a Hitchin moduli space. We also discuss the corresponding limit in the gravitational dual which is described by an eleven-dimensional Membrane-Newton-Cartan theory about a background with an factor.
-
15 Jan 2024
The Differential Geometry and Topology of Four- Dimensional Universal Supergravity
slides: pdf
video: kt
cf.: arXiv:2101.07236
Using the cohomology of the appropriate locally constant sheaf I will explain how to implement the Dirac-Schwinger-Zwanziger integrality condition on four-dimensional classical ungauged supergravity and how to interpret it geometrically in order to obtain its duality-covariant, gauge-theoretic, differential-geometric global model. Using this construction, I will prove that four-dimensional bosonic ungauged supergravity is completely determined by a choice of polarized Siegel bundle defined over the total space of a vertically Riemannian submersion equipped with a complete Ehresmann connection, showing that its gauge sector reduces to a polarized self-duality condition for connections on the underlying polarized Siegel bundle. Furthermore, I will explore the continuous and arithmetic U-duality groups of the theory, characterizing them through short exact sequences and realizing the latter through the automorphism group of the underlying Siegel bundle acting on its adjoint bundle. This elucidates the geometric origin of U-duality and justifies the miraculous existence of U-dualities by describing them as a gauge transformation of the appropriately defined principal bundle.
-
15 Jan 2024
Gauge Theory for String Algebroids
video: kt
In this talk I will explain a moment map construction for string algebroids, a special type of Courant algebroids which arise as Atiyah algebroids of higher principal bundles. The zero locus of our moment map is given by the solutions of the Calabi system, a coupled system of equations which provides a unifying framework for the classical Calabi problem and the Hull-Strominger system in heterotic string theory. Our main results are concerned with the geometry of the moduli space of solutions, and assume a technical condition which is fulfilled in examples. We prove that the moduli space carries a pseudo-Kähler metric with Kähler potential given by the dilaton functional, a topological formula for the metric, and an infinitesimal Donaldson-Uhlenbeck-Yau type theorem. Based on joint work with Rubio and Tipler in arXiv:arXiv:2004.11399 (to appear in JDG) and ongoing joint work with Álvarez-Cónsul and Tellez.
-
15 Jan 2024
Towards Non-Perturbative Lagrangian Field Theory via the Topos of Smooth Sets
video: kt
cf.: arXiv:2312.16301
Any notion of non-pertubative (pre)-quantization of classical field theories, as in particular expected in M-theoretic contexts, presupposes a convenient category within which non-pertubative classical field theory may be rigorously formalised. In this talk, I will describe smooth sets as a category of generalized smooth spaces, completely determined by “how they may be smoothly probed by finite dimensional manifolds”. Formally, this is the “topos of sheaves over the site of Cartesian spaces”. I will then explain how the variational algorithm of (bosonic) classical field theory and the space of on-shell fields naturally take place in smooth sets, along with many more field theoretic concepts. Time permitting, I will indicate how the setting naturally generalizes to include the description of infinitesimal (pertubative) structure, fermionic fields, and (gauge) fields with internal symmetries.
-
15 Jan 2024
Towards Non-Perturbative BV-Theory via Derived Geometry and the Puzzle of Quantisation
video: kt
In this talk I will introduce and discuss a global geometric framework which allows one to encode a natural non-perturbative generalisation of classical Batalin–Vilkovisky(BV-)theory. First, I will set the stage by briefly describing the current state of the art of perturbative BV-theory. Then, I will introduce a concrete model of [derived differential geometry]], whose geometric objects are formal derived smooth stacks (i.e. stacks on formal derived smooth manifolds), and which is obtained by applying Töen-Vezzosi’s homotopical algebraic geometry to the theory of derived manifolds of Spivak and Carchedi-Steffens. I will explain how derived differential geometry is able to capture non-perturbative classical BV-theory by means of examples: scalar field theory and Yang-Mills theory. Finally, I will discuss some open questions, most importantly on quantisation and on applications to global aspects of M-theory.
-
15 Jan 2024
Decomposition of 2D Pure Yang-Mills and the Gross- Taylor String Theory
slides: pdf
video: kt
cf.: arXiv:2307.08729
In this talk, we will attempt to reconcile two different results on two-dimensional pure Yang-Mills theory. Specifically, we will discuss how the fact that 2d pure Yang-Mills is equivalent to a disjoint union of theories, is related to the Gross-Taylor description of 2d pure Yang-Mills as the target-space field theory of a string theory. The Gross-Taylor picture can be understood by first rewriting the Yang-Mills partition function (in a large limit) as a sum of correlation functions in Dijkgraaf-Witten theories for the symmetric group , and then interpreting those Dijkgraaf-Witten correlation functions in terms of branched covers, which leads to the string theory description. We first observe that the decomposition of the pure Yang-Mills aligns perfectly with the decomposition of Dijkgraaf-Witten theory, and then discuss decomposition and the branched covers interpretation. We encounter two puzzles, and to solve them, propose that the Gross-Taylor string theory has a higher-form symmetry.
-
16 Jan 2024
Constraining and Un-constraining Supergravities
slides: pdf
video: kt
I will review various aspects and somewhat surprising consequences of cancellation of (different types of) anomalies in supergravity theories in eight and six dimensions. I will also discuss appearance and importance of exotic (singular, non-spin, non-orientable) backgrounds.
-
16 Jan 2024
Kaluza-Klein Spectrometry for String Theory Compactifications
slides: pdf
video: kt
cf.: arXiv:2212.01135
I will present a powerful new method that for the first time allows us to compute the Kaluza-Klein spectrum of a large class of string theory compactifications, including those arising in maximal gauged supergravities and beyond. This includes geometries with little to no remaining (super-)symmetries, completely inaccessible by previous methods. I will show how these insights can be used to holographically compute the anomalous dimensions of protected and unprotected operators in strongly-coupled CFTs, as well as to study global properties of their conformal manifolds. I will also show how the method can be used to determine the perturbative stability of non supersymmetric AdS vacua. We will see the importance of higher Kaluza-Klein modes to the physics of string compactifications, e.g. in realising the compactness of moduli spaces, restoring supersymmetry that is lost in a consistent truncation, and in destabilising vacua that appear to stable in lower-dimensional supergravities.
-
16 Jan 2024
Cubic Forms, Anomaly Cancellation and Modularity
video: kt
cf.: arXiv:2005.02344
Freed and Hopkins developed an algebraic theory of cubic forms, which is an analogy to the theory of quadratic forms in topology. They are motivated by the Witten-Freed-Hopkins anomaly cancellation formula in M-theory, which equals a cubic form arising from an bundle over a 12 dimensional spin manifold to the indices of twisted Dirac operators on the manifold. In this talk, we will first review the Witten-Freed-Hopkins anomaly cancellation formula and the algebraic theory of cubic forms, and then show that the cubic forms as well as the anomaly cancellation formula can be naturally derived from modular forms that we construct inspired by the Witten genus and the basic representation of affine . Following this approach, we obtain new cubic forms and anomaly cancellation formulas on non-spin manifolds and thus provide a unified way to obtain anomaly cancellation formulas of this type. This is based on our joint work with Prof. Ruizhi Huang, Prof. Kefeng Liu and Prof. Weiping Zhang.
-
16 Jan 2024
Topological-Holomorphic Gauge Theory: From Langlands Duality of Holomorphic Invariants to Mirror Symmetry of Quasi-Topological Strings
slides: pdf
video: kt
cf.: arXiv:2305.15965
We perform a topological-holomorphic twist of supersymmetric gauge theory on a four-manifold of the form , and unravel the mathematical implications of its physics. In particular, we consider the cohomology of different linear combinations of the resulting scalar supercharges under S-duality, whence we would be able to derive novel topological and holomorphic invariants of and their Langlands duals. As the twisted theory can be topological along such that we can dimensionally reduce it to 2d, via the effective sigma-model on , we can also relate these 4d invariants and their Langlands duals to the mirror symmetry of Higgs bundles and that of quasi-topological strings described by the sheaf of chiral differential operators.
-
16 Jan 2024
Double Copy, Double Field Theory & Homotopy Algebras
video: kt
The double copy denotes a technology to relate the scattering amplitudes of Yang-Mills theory to those of gravity. While enormously successful at the level of scattering amplitudes, until recently there was no first-principle understanding of how to derive such relations. Such an understanding would be needed in order to describe, for instance, a double copy of classical solutions. I present an approach based on homotopy algebras such as L-infinity algebras that allows one to provide such a first-principle derivation, at least to some finite order in perturbation theory. To this end I review how to formulate Yang-Mills theory as an L-infinity algebra, how to “strip off” color to obtain a different kind of homotopy algebra and, finally, how to combine two copies of these exotic algebras to obtain the L-infinity algebra of gravity in the form of double field theory.
-
16 Jan 2024
Atiyah Algebroids for Higher and Groupoid Gauge Theories
slides: pdf
video: kt
We present an Atiyah algebroid picture for higher and groupoid gauge theories. Common to both is the fact that straightforward definitions of curvatures are only suitable for partially flat cases. Instead, one has to adjust the underlying cocycle relations, leading to new curvatures and gauge transformations. The Atiyah algebroid picture I sketch provides a good idea about the origin of adjustments and why they are required even in the relative conventional case of groupoid gauge theories.
-
17 Jan 2024
Self-Dual -Form Gauge Fields and the Topology of the Graviton
slides: pdf
video: kt
cf.: arXiv:2307.04748
Sen’s action for a -form gauge field with self-dual field strength coupled to a spacetime metric involves an explicit Minkowski metric and the presence of this raises questions as to whether the action is coordinate independent and whether it can be used on a general spacetime manifold. A natural generalisation of Sen’s action is presented in which the Minkowski metric is replaced by a second metric on spacetime. The theory is covariant and can be formulated on any spacetime. The theory describes a physical sector, consisting of the chiral -form gauge field coupled to the dynamical metric , plus a shadow sector consisting of a second chiral -form and the second metric. The resulting theory is covariant and can be formulated on any spacetime. A spacetime with two metrics has some interesting geometry and some of this is explored here and used in the construction of the interactions. The action has two diffeomorphism-like symmetries, one acting only on the physical sector and one acting only on the shadow sector, with the spacetime diffeomorphism symmetry arising as the diagonal subgroup.
-
17 Jan 2024
The AI Mathematician
video: kt
We summarize how AI can approach mathematics in three ways: theorem-proving, conjecture formulation, and language processing. Inspired by initial experiments in geometry and string theory, we present a number of recent experiments on how various standard machine-learning algorithms can help with pattern detection across disciplines ranging from algebraic geometry to representation theory, to combinatorics, and to number theory.
-
17 Jan 2024 (talk canceled last minute and postponed to 31 Jan)
Geometry and Dualities of Decoupling Limits in String Theory and M-Theory
cf.: arXiv:2311.10564
Our understanding of M-theory is based on a duality web connecting different limits of the theory. I’ll discuss the extension of this duality web to a wide variety of decoupling limits related by duality to the null reduction of M-theory (and hence to the proposal that M-theory can be described by Matrix theory). From a modern perspective, these limits involve non-relativistic geometries, leading to new variants of supergravity in 11- and 10-dimensions. I’ll discuss how to systematically explore these corners of M-theory, following the roadmap of arxiv.org/abs/2311.10564.
-
17 Jan 2024
M-Theory and Hypothesis H
video: kt
I will survey the (co)homotopical perspective on the fields and branes in M-theory, showcasing several recent developments. This talk highlights the classical/prequantum aspects, while the talk by Urs Schreiber will highlight the quantum aspects.
-
17 Jan 2024
Introduction to Quantum Hypothesis H
video: kt
A famous hypothesis in string theory says that the RR-fields in 10d supergravity are subject to “flux quantization” in topological K-cohomology theory. From a modernized point of view of rational homotopy theory, analogous reasoning applies to the C-field in 11d supergravity and suggests that its flux should be quantized in the “unstable CoHomotopy” cohomology theory of Borsuk, Pontrjagin and Spanier. I’ll survey this “Hypothesis H” with focus on its implications for quantum observables on intersecting branes. This is joint work with Hisham Sati. Notes are available at: ncatlab.org/schreiber/show/Introduction+to+Hypothesis+H.
Apr 2024
17 April 2024
Workshop: Field Theory and Gravity – Classical and Quantum
-
Alberto Cattaneo (Univ. Zurich):
BV pushforward and applications
In the BV formalism the spaces of fields are presented as complexes whose cohomology returns the physical content. Different but equivalent complexes may be used, which turns out to be important conceptually and in practice. One useful operation is that of a partial integration (BV pushforward), which produces a chain map that, under some assumptions, is a quasiisomorphism. This has several applications: construction of observables (often as -representations), renormalization à la Wilson, highly nontrivial equivalences of theories. I will discuss some examples.
-
Alberto Cattaneo (Univ. Zurich):
Gravity: bulk, boundary, corners
I will review four-dimensional gravity in the coframe-and-connection formulation (a.k.a. Palatini–Cartan formalism) and what it entails on boundaries (e.g., on Cauchy surfaces) and on corners (e.g., surfaces at infinity or surfaces around singularities in space). This full analysis will require the BV, the BFV and related formalisms and their interplay.
-
Grigorios Giotopoulos (NYU AD):
Supergravity as Super-Cartan Geometry on Super-spacetime
It is well-known that supergravity admits a super-spacetime formulation, which in modern language revolves around super Cartan geometry modeled on a coset space of the corresponding super-Poincaré group. After describing ordinary gravity in terms of Cartan geometry, I will recall its supersymmetric extension via the addition of a (fermionic) spinor – the gravitino. In passing, I shall explain how the correct mathematical language to describe such fermionic fields on a bosonic spacetime is that of (smooth) super sets. I will then recall one of its standard super-spacetime formulations, as a theory of a single super-Cartan connection obeying the analogous field equations, paralleling that of ordinary gravity. In D=11, supersymmetry demands the existence of a C-field with 4-form flux density – along with its (on-shell) dual 7-form flux . I will conclude by describing a concise formulation of on-shell supergravity as a form of (higher) super-Cartan geometry, by the sole demand that a certain super-enhancement of the pair is a -cocycle. This exhibits D=11 supergravity as being manifestly compatible with flux-quantization.
(This is joint work with Hisham Sati and Urs Schreiber, cf. arXiv:2403.16456).
-
Urs Schreiber (NYU AD):
Flux-Quantization of 11D Supergravity on Superspace
Theories of (higher dimensional) supergravity famously contain (higher) gauge fields. However, traditionally (notably in all Lagrangian formulations of supergravity) these have been discussed only in the case of gauge potentials given by globally defined differential forms. In reality, (higher) gauge fields have additional global degrees of freedom appearing as cocycles in some generalized nonabelian differential cohomology-theory and determining the torsion charges carried by small numbers of branes sourcing these fields.
I will first recall the general mechanism of flux quantization that is needed to specify the complete gauge potentials of higher gauge fields, together with some “well-known” examples, and then address the case of D=11 supergravity. Here a miracle occurs: The flux quantization of the C-field in D=11 supergravity naturally exists not just on phase space but on all of spacetime, in fact on super-spacetime, where the existence of a flux-quantized C-field already implies the full higher-Maxwell-Rarita-Schwinger-Einstein-equations of motion.
(This is joint work with Grigorios Giotopoulos and Hisham Sati, cf. arXiv:2403.16456).
19-21 April 2024
Conference: Homotopy Type Theory and Computing – Classical and Quantum
home page: nyuad.nyu.edu/en/events/2024/april/homotopy-type-theory-and-computing.html
live stream: nyu.zoom.us/j/93101580794

The aim of this conference is to discuss Homotopy Type Theory Theory (
HoTT) as a substrate for computing and verification in software development, in synthetic homotopy theory, and possibly in application to (topological) quantum computing/simulation.Some talks will focus on recent progress on the general issue of running
HoTTprograms, in view of the univalence axiom: such as via “cubical TT” or the more recent “higher observational TT”. Other talks will focus on design patterns for practical (quantum) programming and certification languages, notably via modal types and monadic effects (in modal extensions of HoTT).In this vein, our local speakers will present a point of contact between modal
HoTTand Quantum: the recently developed “Linear HoTT” (LHoTT) that equips classicalHoTTwith dependent “linear” types which may be thought of as quantum data types. TheLHoTTapproach to quantum programming interprets a significant fragment of the Proto-Quipper-language, now with identity types enabling full verification.The conference is to bring this theoretical progress into contact with efforts to use (
L)HoTTand related languages like Proto-Quipper for actual (quantum) computing, simulation and verification.
Schedule:
| 19th | 20th | 21st | |
|---|---|---|---|
| 9:00 | Buchholtz | Lee | Shulman |
| 10:00 | Mörtberg | Riley | Kovács |
| 11:00 | Lamiaux | Paykin | Riley |
| 12:00 | Ljungström | Finster | lunch |
| 13:00 | lunch | lunch | |
| 14:00 | Wärn | Gratzer | |
| 15:00 | Schreiber | Sterling | |
| 16:00 | Myers | Altenkirch | |
| 17:00 | Rand | Angiuli |
Paykin Wärn Myers Kovács Finster Schreiber X Altenkirch Lamiaux Riley Buchholtz Lee
Talks:
-
Thorsten Altenkirch (Univ. Nottingham):
Univalence Without an Interval
video: kt
We are developing a new formulation of univalent type theory (known as HoTT) which doesn’t use an interval type. The first step is to formulate a type theory with internal parametricity which can be modelled using BCH cubes - see our POPL paper [1]. As a next step we identify a fibrant universe using a higher coinductive type.
This is joint work with Yorgo Chamoun, Ambrus Kaposi and Mike Shulman
[1] Altenkirch, T., Chamoun, Y., Kaposi, A., & Shulman, M. (2024). Internal parametricity, without an interval Proceedings of the ACM on Programming Languages (POPL) 8 (2024) 2340-2369 [arXiv:2307.06448, doi:10.1145/3632920]
-
Carlo Angiuli (Indiana Univ.)
Normalization: Running Open Terms
video: kt
This talk will survey the normalization problem for type theory, in anticipation of upcoming talks at this conference by Shulman and Kovács. I will attempt to define normalization in general, before focusing on the simply-typed lambda calculus, its (beta-eta) normal forms, and normalization by evaluation. I will also discuss dependent types, the relationship between computation and normalization, and a forthcoming expository resource.
-
Ulrik Buchholtz (Univ. Nottingham)
Primitive recursive (homotopy) type theory
video: kt
I’ll present a subsystem of Martin-Löf type theory where all functions from Nat to Nat are primitive recursive. The soundness proof involves a gluing construction for a sheaf topos model constructed from a site of primitive recursive functions. Then I’ll use this as a starting point for some speculations about geometric type theory and its computational aspects. This is based on joint work with Johannes Schipp von Branitz.
-
Eric Finster (Univ. Birmingham):
A Tour of Parameterized Spectra
video: kt
This talk will be a survey of some of the defining characteristics of the infinity-topos of parameterized spectra. I will try to describe both “external” properties, such as what this topos classifies as a higher geometric theory, as well as “internal” properties, that is, the various additional axioms satisfied by its internal logic. Where possible, I will try to explain how to express well-known constructions from homotopy theory in the internal language of this topos.
-
Daniel Gratzer (Aarhus Univ.):
Towards a category of spaces in simplicial type theory
video: kt
Simplicial type theory as introduced by Riehl and Shulman and developed by Buchholtz, Martı́nez, Weinberger, and others enables a type-theoretic synthetic study of ∞-categories. A major absence from the existing results in simplicial type theory is the absence of basic “generating” ∞-categories e.g., the ∞-categories of groupoids. We present a work-in-progress construction of a type satisfying the properties expected of the ∞-category of ∞-groupoids or, equivalently, the universal left fibration. We draw on existing work by Weaver and Licata to construct a universe of ∞-groupoids within an extension of multimodal HoTT/homotopy MTT tooled for synthetic cubical spaces and argue that it lies within the subcategory of (synthetic) simplicial spaces and satisfies the expected properties (Segalness, Rezkness, directed univalence) and is closed under the expected connectives.
-
András Kovács (Univ. Gothenburg):
Efficient Evaluation for Cubical Type Theories
video: kt
slides: pdf
There are numerous interesting computations in cubical type theory, mostly in relation to synthetic homotopy theory, which are too expensive to perform in existing systems. One way to try to address this is to optimize the involved definitions. Another way, that I focus on in this talk, is to improve evaluation for the theory itself. I present a recent implementation of a CTT with major performance improvements. Broadly speaking, the benefits stem from a) systematically omitting unnecessary computation b) exploiting the canonicity property of the CTT when computation depends on interval variables but not free variables with fibrant types.
-
Thomas Lamiaux (ENS Paris):
Computing Cohomology Rings in Cubical Agda
video: kt
In this talk, we will discuss the formalization of cohomology rings in Cubical Agda, and how we computed a few basic examples. We will particularly focus on: 1. How the choice of a data type representation influence formalisation, in our case for representing polynomials and cohomology rings 2. How suitable representations can be used to compute cohomology rings 3. Where computation would be helpful, how it is limited in practice, and how we can still recover some computation to help us with our proof.
-
Dongho Lee (Dalhousie Univ.)
A Concrete Categorical Semantics for Proto-Quipper Language and Dynamic Lifting
slides: pdf
video: kt
In this talk, we discuss a concrete categorical semantics of Proto-Quipper-L, a quantum circuit description language with dynamic lifting. The language is an extension of linear lambda-calculus with quantum channel constants (which represent tree structure of gates) and circuit operations (which are box and unbox) where terms can have tree shapes. The type system roughly comes from the multiplicative intuitionistic linear logic where the term represents the proof. The categorical semantics of the language is built upon the linear and non-linear model for linear logic by Benton and coproduct completion as the categorical semantics of Proto-Quipper-M by Rios and Selinger while we give a concrete categorical model for diagrams based on graphical calculus. For the computational effect of dynamic lifting we introduce branching monad and give an interpretation of terms in the Kleisli category.
-
More cellular (co)homology in HoTT
video: kt
In this talk, I’ll present some ongoing work with Anders Mörtberg and Loïc Pujet on the development and computer formalisation of cellular homology and cohomology. Cellular cohomology was first studied in HoTT by Buchholtz and Favonia who constructed cellular cohomology groups and showed that these define a cohomology theory. This was done by proving their construction equivalent to the usual construction of cohomology groups via Eilenberg-MacLane spaces. I will present an alternative approach to cellular (co)homology (à la Buchholtz & Favonia) using a more traditional framework building on the theory of cellular approximations. One benefit of this approach is that it works uniformly for homology and cohomology. In particular, I will show you some versions of cellular approximation theorems we can prove constructively in HoTT and discuss how these can be used to get functorial cohomology and homology theories. Another benefit of the approach by cellular approximation is that it makes the definition of the cup product on cellular cohomology rather direct. If time permits, I will discuss also this construction and whether it can aid in cohomology computations, both in the mathematical sense and in the sense of normalisation in constructive proof assistants like Cubical Agda.
-
Anders Mörtberg (Stockholm University):
Computational Proofs in Synthetic Homotopy Theory
video: kt
Cubical type theories provide computational meaning to HoTT, making it possible to simplify proofs in synthetic homotopy theory and sometimes even reducing whole arguments purely to computer computations. A classic example is the Brunerie number which we recently managed to simplify so that it becomes computable in just a few seconds in Cubical Agda. I will discuss this and other similar proofs by computation that we have done. I will also discuss various examples of things that we have not managed to compute and work in progress into making Cubical Agda able to compute more things for us.
-
David Jaz Myers (NYU Abu Dhabi):
Topological Quantum Gates
video: kt
cf. arXiv:2303.02382
Despite the evident necessity of topological protection for realizing scalable quantum computers, the conceptual underpinnings of topological quantum logic gates had arguably remained shaky. Building on recent results on defect branes in string/M-theory and on their holographically dual anyonic defects in condensed matter theory, here we explain how the specification of realistic topological quantum gates, operating by anyon defect braiding in topologically ordered quantum materials, has a surprisingly slick formulation in parameterized point-set topology, which is so fundamental that it lends itself to certification in modern homotopically typed programming languages such as cubical Agda. We propose that this remarkable confluence of concepts may jointly kickstart the development of topological quantum programming proper by providing a powerful paradigm for simulating and verifying topological quantum computing architectures with high-level certification languages aware of the actual physical principles of realistic topological quantum hardware.
In this talk, we will present the description of these topological quantum gates in homotopy type theory and describe the use of cubical type theory as a certification language for topological quantum computing. We will focus on the definition of the configuration spaces in cubical type theory, which play a crucial role in the construction of the space of conformal blocks as a twisted cohomology group.
-
Jennifer Paykin (Intel Labs):
Symplectic Types for a Clifford Lambda Calculus
video: kt
Can quantum programming languages move beyond gate-based programming? In this talk I will present work in progress where quantum algorithms (specifically, Clifford unitaries over qudits) are expressed as functions on compact Pauli encodings. Inspired by the fact that projective Cliffords correspond to center-fixing automorphisms on the Pauli group, we develop a type system where well-typed expressions correspond to symplectic morphisms—that is, linear transformations that respect the symplectic form. This language is backed up by a robust categorical and operational semantics, and well-typed functions can be efficiently simulated and synthesized into circuits. The resulting linear type system and semantics is a promising candidate for synthetic mathematical reasoning using linear HoTT.
-
Robert Rand (Univ. Chicago):
Verifying the ZX-calculus and its Friends
video: kt
cf.: arXiv:2311.11571
We seek to verify the ZX-calculus, a powerful tool for representing and reasoning about quantum computation. ZX-diagrams are typically represented as adjacency-based graphs, reflecting the guiding principle that “only connectivity matters”. In the context of formal theorem provers like Coq, however, such graphs are difficult to reason about, especially when we seek to give them semantics. To address this gap, we introduce
VyZX, a verified library for reasoning about the ZX-calculus, using inductive constructs that arise naturally from category theoretic definitions. We extendVyZXto reason about a variety of monoidal categories, provided they satisfy an appropriate set of coherence conditions. -
Mitchell Riley (NYU Abu Dhabi):
Linear HoTT and Quipper
video: kt
slides: pdf
notes: pdf
Linear HoTT is an extension of HoTT with linear type formers. Like the Proto-Quipper family of languages, Linear HoTT can be used to specify (linear) quantum circuits parameterised by (non-linear) classical data. Because we have all of ordinary Martin-Löf Type Theory at our disposal, there is the prospect of formally verifying properties of our quantum programs in the same language that they are specified. In this talk I will give a new, simpler set of rules for Linear HoTT and sketch a translation of Quipper into this system.
-
Mitchell Riley (NYU Abu Dhabi):
Tiny Objects in Type Theory
video: kt
slides: pdf
cf. arXiv:2403.01939
I will present an extension of Martin-Löf Type Theory that contains a tiny object; a type for which there is a right adjoint to the formation of function types as well as the expected left adjoint. I will suggest a couple of potential applications and sketch a normalisation algorithm.
-
Urs Schreiber (NYU AD):
Towards Quantum Programming via Linear Homotopy Types
notes: web
video: kt
Remarkably, among the -toposes into which HoTT interprets are “tangent -toposes” of parameterized module spectra, which behave like semantics for an enhancement of HoTT by dependent *linear* homotopy types, neatly combining the linear aspect of typed quantum programming languages (like Proto-Quipper) with homotopy-theoretic aspects needed for future topological quantum languages. I will survey this LHoTT-perspective on quantum systems, developed jointly with Hisham Sati (“Topological Quantum Gates in HoTT” arXiv:2303.02382, “Entanglement of Sections” arXiv:2309.07245, “The Quantum Monadology” arXiv:2310.15735, “Quantum and Reality” arXiv:2311.11035).
-
Michael Shulman (Univ. San Diego):
Towards an Implementation of Higher Observational Type Theory
video: YT
Higher Observational Type Theory is a third style of Homotopy Type Theory, contrasting with Book HoTT and Cubical Type Theory. It is characterized by a definition of identity types by recursion on the base type: the identity type of a product type is defined to be a product of identity types, and so on. Extensionality principles like funext, univalence, and bisimulation then hold essentially by definition, rather than only up to equivalence. Like Cubical Type Theory, Higher Observational Type Theory can be built by defining a fibrancy predicate in a non-univalent substrate theory, which in this case is a form of internally parametric type theory. Altenkirch’s talk describes a canonicity proof for this substrate; I will sketch a normalization algorithm for it (sans proof), and then demonstrate a prototype implementation of this algorithm. This is joint work in progress with Altenkirch, Kaposi, and Uskuplu.
-
Jonathan Sterling (Univ. Cambridge):
Baby steps in higher domain theory
video: kt
I present some preliminary results obtained with Leoni Pugh concerning partial map classifiers in higher domain theory, realised in a version of Riehl and Shulman’s simplicial type theory extended by Phoa’s principle for the simplicial interval.
-
David Wärn (Univ. Gothenburg):
The zigzag construction
video: kt
The zigzag construction gives a more or less explicit sequential colimit description for certain pullbacks of pushouts of spaces. It generalises the fact that the free groupoid on a bipartite graph can be understood in terms of zigzags of edges modulo backtracking. It remains to be understood to what extent this description can be used for computations. This requires understanding what happens in each step of the construction. In this talk, I will present the construction with a view toward generalisations and applications.
May 2024

27 May - 31 May 2024
Conference: Quantum Information and Quantum Matter
home page: nyuad.nyu.edu/en/events/2024/may/quantum-information-and-quantum-matter.html
Talks:
-
Herbert Schoeller (RWTH Aachen University):
Universal Properties of the Boundary Charge
The boundary charge is an interesting observable to characterize ground state properties of insulators. Its universal properties and relevance for topology, bulk-boundary correspondence, integer and fractional quantum Hall effect, charge quantization, universal fluctuations, and characterization of phase transitions is reviewed in this talk. In particular, it is demonstrated that two fundamental invariants characterize the properties of the boundary charge, which are present independent of symmetries, and are the basis for the explanation of the quantum Hall effect and the rational quantization of boundary and interface charges.
-
Christina Psaroudaki (École Normale Supérieure (ENS)):
Quantum Functionalities of Magnetic Skyrmions
Magnetic nanoskyrmions develop quantized helicity excitations, and the quantum tunneling between nanoskyrmions possessing distinct helicities is indicative of the quantum nature of these particles. Experimental methods capable of non-destructively resolving the quantum aspects of topological spin textures, their local dynamical response, and their functionality now promise practical device architectures for quantum operations. With abilities to measure, engineer, and control matter at the atomic level, nanoskyrmions present opportunities to translate ideas into solid-state technologies. This talk aims to discuss the basic concept of a magnetic skyrmion qubit, its advantages, and challenges in this new research avenue in quantum magnetism and quantum information.
-
Ajit C. Balram (Homi Bhabha National Institute, India):
Fingerprints of Composite Fermion Lambda Levels in Scanning Tunneling Microscopy
cf. arXiv:2312.06779
Composite fermion (CF) is a topological quasiparticle that emerges from a non-perturbative attachment of vortices to electrons in strongly correlated two-dimensional materials. Similar to non-interacting fermions that form Landau levels in a magnetic field, CFs can fill analogous “Lambda’‘ levels, giving rise to the fractional quantum Hall (FQH) effect of electrons. Here, we show that Lambda levels can be directly visualized through the characteristic peak structure in the signal obtained via spectroscopy with the scanning tunneling microscopy (STM) on a FQH state. Complementary to transport, which probes low-energy properties of CFs, we show that high-energy features in STM spectra can be interpreted in terms of Lambda levels. We numerically demonstrate that STM spectra can be accurately modeled using Jain’s CF theory. Our results show that STM provides a powerful tool for revealing the anatomy of FQH states and identifying physics beyond the non-interacting CF paradigm.
-
Yuxin Zhao (University of Hong Kong):
Projective Crystal Symmetry and Novel Topological Phases
Roughly a decade after the birth of quantum mechanics, E. Wigner pointed out a fundamental principle of quantum mechanics: symmetry groups are projectively represented. He applied this principle to study the Poincaré group. While the Poincaré group is the unique spacetime group of relativistic particles, its counterpart in condensed matter consists of various space groups for crystals and the time reversal. In this sense, the projective representation of condensed-matter spacetime groups is much richer and of fundamental importance. However, projective crystal symmetry was not systematically investigated until recently. In this talk, I will introduce the general theory of projective crystal symmetry algebras and show some of their novel consequences in topological matter. Particularly, they can lead to -space non-symmorphic symmetries, which can significantly expand the framework of crystalline topological phases.
-
Leandro Aolita (Quantum Research Center, TII, Abu Dhabi):
Tensor Network Use Cases: From Quantum Process Tomography to Computational Fluid Dynamics
In this talk, I will describe two recent applications of tensor networks. In the first part, I will present an efficient technique for quantum process learning, a quintessential primitive to characterize quantum devices. This combines a tensor network representation of the target quantum channel with a data-driven optimization inspired by unsupervised machine learning. These results go far beyond state-of-the-art, providing a practical and timely tool for benchmarking quantum circuits in current and near-term quantum computers. In the second part, in turn, I will briefly describe a recently developed (classical) quantum-inspired algorithm for solving the Navier-Stokes equation in complex geometries, based on tensor trains. This is a full-stack method to solve for incompressible fluids with memory and runtime scaling poly-logarithmically in the mesh size. Our framework is based on matrix product states (a.k.a tensor trains), a powerful compressed representation of quantum states. It is complete in that it solves for flows around immersed objects of arbitrary geometries, with non-trivial boundary conditions, and self-consistent in that it can retrieve the solution directly from the compressed encoding, i.e. without ever passing through the expensive dense-vector representation. This machinery lays the foundations for a new generation of potentially radically more efficient solvers of real-life fluid problems.
-
Ingo Roth (Quantum Research Center, TII, Abu Dhabi):
Robustly Learning the Hamiltonian Dynamics of a Superconducting Quantum Processor
The required precision to perform quantum simulations beyond the capabilities of classical computers imposes major experimental and theoretical challenges. The key to solving these issues are highly precise ways of characterizing analog quantum simulators. Here, we report on theoretical and experimental work on estimating the free Hamiltonian parameters of bosonic excitations in a superconducting-qubit analog quantum simulator from measured time-series. We achieve the required levels of precision in estimating the Hamiltonian parameters by maximally exploiting the model structure, making it robust against noise and state-preparation and measurement (SPAM) errors. Our learning algorithm is highly scalable both in terms of the required amounts of data and post-processing. To achieve this, we develop a new super-resolution technique for frequency extraction from matrix time-series and make use of constrained manifold optimization for the eigenspace reconstruction. For up to 14 coupled superconducting qubits on two Sycamore processors, we identify the Hamiltonian parameters - verifying the implementation on one of them up to sub-MHz precision - and construct a spatial implementation error map for a grid of 27 qubits. Our results constitute a fully characterized, highly accurate implementation of an analog dynamical quantum simulation and introduce a diagnostic toolkit for understanding, calibrating, and improving analog quantum processors.
-
Enrique Solano (Kipu Quantum, Berlin, Germany):
Useful Quantum Computing in the NISQ Era
I will describe digital, analog, and digital-analog quantum computing paradigms. Furthermore, I will discuss the possibility of reaching quantum advantage for industry use cases with current quantum computers in trapped ions, superconducting circuits, neutral atoms, and photonic systems.
-
Javad Shabani (NYU New York):
Experimental Routes in Realization of Topological Josephson Junctions
Majorana bound states, which are their own antiparticles, are predicted to emerge as zero-energy modes localized at the boundary between a topological superconductor and a topologically trivial region. Unlike BCS superconductors, nature has not provided us unambiguous topological superconductors. However, it was realized that by interfacing BCS superconductors and semiconductors with strong spin-orbit coupling it is possible to create a system that can host topological states. Hence epitaxial superconductors and semiconductors have emerged as an attractive materials system with atomically sharp interfaces and broad flexibility in device fabrications incorporating Josephson junctions. We discuss the basics of topological superconductivity and provide insight on how to go beyond current state-of-the-art experiments. We argue that the ultimate success in realizing Majorana bound state physics relies on the observation of non-trivial fusion and braiding experiments.
-
Frank Schindler (Imperial College London):
Interaction-Induced Crystalline Topology of Excitons
Topologicalband theory has celebrated various successes over the last few years, such as the recent classifications of crystalline materials based on their space group symmetry. We are currently witnessing a drive to generalise this theory to the case where interactions between electrons become relevant, with much work focused on ground states. As an alternative direction, we here study the topology of interaction-induced excitations, specifically excitons in semiconductors. In my talk, I will give a pedagogical introduction to the classification and bulk-boundary correspondence of exciton band structures based on inversion symmetry.
-
Adrien Bouhon (Nordic Institute for Theoretical Physics, Sweden):
From the Homotopy Groups of Real Grassmannians to the Quantum Geometry of Many-Band Systems
I first review the homotopy classification of band structures for crystalline systems described by a real Bloch Hamiltonian. These systems, both of fermionic or bosonic types, abound in nature as they merely require the combination of an anti-unitary symmetry (e.g. time reversal) and a twofold unitary symmetry (i.e. inversion, Pi-rotation, or mirror). The relevant classifying spaces, i.e. the real Grassmannians and the real flag manifolds, exhibit a rich geometric structure leading to a manifold of topological phases in all dimensions. I then introduce a completely general framework, based on the Pluecker imbedding of Grassmannians, to capture the Riemannian geometry of these “real” topological phases, that naturally extends to many-band contexts. While this approach permits the systematic homotopy-based modeling of few-band systems — greatly facilitating the design of such phases in synthetic matter — it culminates with the definition of a new invariant capturing the Euler class of many-band (i.e. beyond rank-2) subspaces.
-
András Pályi (Budapest University of Technology and Economics):
Weyl Points Beyond Band Structures: Classical Mechanics, Spin Qubits, Josephson Junctions
In the past decade, research on Weyl semimetals has evolved into a major theme within condensed-matter physics. Defining characteristics of Weyl semimetals are Weyl points, i.e., touching points (a.k.a. degeneracy points or conical intersections) between neighbouring energy bands in the electronic band structure. Further characteristics of such a Weyl point are its robustness against fluctuations, and the linear energy dispersion in its vicinity. In this talk, I will discuss the simple mathematical origin of the robustness of Weyl points, and illustrate that similar degeneracy points appear in a plethora of physical systems described by parameter-dependent matrices, e.g., in the frequency spectrum of coupled linear oscillators [1], and in the energy spectrum of interacting spin qubits [2,3,4] or Josephson junctions [5,6]. I will also highlight universal patterns describing the creation, annihiliation, merger, and separation of Weyl points as control parameters are varied [6,7]. Interestingly, much of this universal behaviour is described by known results from a specific branch of mathematics called singularity theory.
[1] Z. Guba, Gy. Frank, G. Pinter, A. Palyi, Weyl points in ball-and-spring mechanical systems, arXiv:2302.08241
[2] Z. Scherubl, A. Palyi, et al., Observation of spin-orbit coupling induced Weyl points in a two-electron double quantum dot, Comms. Phys. 2, 108 (2019), arXiv:1804.06447
[3] Gy. Frank, Z. Scherubl, Sz. Csonka, G. Zarand, A. Palyi, Magnetic degeneracy points in interacting two-spin systems: geometrical patterns, topological charge distributions, and their stability, Phys. Rev. B 101, 245409 (2020), arXiv:1910.02831
[4] A. Sen, Gy. Frank, B. Kolok, J. Danon, A. Palyi, Classification and magic magnetic-field directions for spin-orbit-coupled double quantum dots, Phys. Rev. B 108, 245406 (2023), arXiv:2307.02958
[5] Gy. Frank, D. Varjas, G. Pinter, A. Palyi, Weyl-point teleportation, Phys. Rev. B 109, 205415 (2024), arXiv:2112.14556
[6] Gy. Frank, G. Pinter, A. Palyi, Singularity theory of Weyl-point creation and annihilation, arXiv:2309.05506
[7] G. Pinter, Gy. Frank, D. Varjas, A. Palyi, Birth Quota of Non-Generic Degeneracy Points, arXiv:2202.05825
-
Rafael Chaves (International Institute of Physics (IIF-UFRN))
Enhancing Non-Classicality Detection with Interventional Data
Generalizations of Bell's theorem, particularly within quantum networks, are now being analyzed through the causal inference lens. However, the exploration of interventions, a central concept in causality theory, remains unexplored. As will be discussed, if we are not limited to observational data and can intervene in our experimental setup, then we can witness quantum violations of classical causal bounds even when no Bell-like violation is possible. That is, through interventions, the quantum behavior of a system that would seem classical otherwise can be demonstrated. We will then present a photonic experiment implementing those ideas and consider applications of this framework for measurement-based quantum computation, quantification of causality in quantum gates and quantum network protocols.
[1] M. Gachechiladze et al. “Quantifying causal influences in the presence of a quantum common cause.” Physical Review Letters 125, 230401 (2020).
[1] I. Agresti et al. “Experimental test of quantum causal influences.” Science Advances 8, eabm1515 (2022).
[1] P. Lauand et al. “Quantum non-classicality in the simplest causal network.” arXiv preprint arXiv:2404.12790 (2024).
-
Sonia Haddad (University of Tunis El Manar):
Altermagnetism Emerging from Electronic Correlations
While altermagnetic materials are characterized by a vanishing net magnetic moment, their symmetry in principle allows for the existence of an anomalous Hall effect (AHE). Here we introduce a model with altermagnetism in which the emergence of an AHE is driven by interactions. This model is grounded in a modified Kane-Mele framework with antiferromagnetic (AFM) spin-spin correlations. Quantum Monte Carlo simulations show that the system undergoes a finite temperature phase transition governed by a primary AFM order parameter accompanied by a secondary one of Haldane type. The emergence of both orders turns the metallic state of the system, away from half-filling, to an altermagnet with a finite anomalous Hall conductivity. A mean field ansatz corroborates these results, which pave the way into the study of correlation induced altermagnets with finite Berry curvature.
-
Gianluigi Catelani (Quantum Research Center, TII, Abu Dhabi):
Improved Modelling of Superconducting Qubits
More accurate control and reduced error rates are needed for superconducting circuits to move beyond the current NISQ era, and improving our understanding of superconducting qubits can help towards this goal. In this talk I will discuss two recent advances and their impacts on qubit control and errors. After briefly reviewing the standard tunnel model of a Josephson junction, I will introduce a more realistic model which is needed to accurately describe spectroscopic data [1]. Next, I will show how a form of so-called “gap engineering’’, in which the values of the superconducting gap on the two sides of a junction are properly chosen, can mitigate errors related to quasiparticles [2]. Finally, I will consider implications for a proposed topological qubit implementation (see [3] and references there).
[1] D. Willsch et al., Nat Phys (2024)
[2] G. Marchegiani et al., PRX Quantum 3, 040338 (2022)
[3] J. Krause et al., arXiv:2403.03351
-
Felix von Oppen (Dahlem Center for Complex Quantum Systems, Freie Universität Berlin):
Theory of the Quantum Twisting Microscope
2D van der Waals systems have become a major quantum materials platforn, exhibiting a plethora of correlated electronic phases. Beyond conventional transport experiments, much information on van-der-Waals materials derives from local probes such as scanning tunneling microscopy as well as scanning single-electron-transitor and scanning SQUID measurements. The quantum twisting microscope is a powerful new instrument complementing previously existing local probes. Rather than measuring the local tunneling current at the atomic scale as in scanning tunneling microscopy, it relies on coherent tunneling across a twistable finite-area junction formed at the interface between van der Waals systems placed on a scanning tip with a flat pyramidal top and a substrate. Due to the finite contact area, tunneling is momentum conserving up to reciprocal lattice vectors of the tip and sample layers. In this talk, I discuss the theory of the quantum twisting microscope. While elastic tunneling dominates the tunneling current at small twist angles, the momentum mismatch between the K-points of tip and sample at large twist angles can only be bridged by inelastic scattering. The latter allows for probing collective-mode dispersions along certain lines in reciprocal space by measuring the tunneling current as a function of twist angle and bias voltage. We illustrate this modality of the quantum twisting microscope by developing a systematic theory for measuring phonon dispersions using graphene-graphene junctions. In addition to providing a case study for probing collective modes, our results inform the quest to understand the origin of superconductivity in twisted bilayer graphene.
-
Robert-Jan Slager (University of Cambridge):
Non-abelian Phases, Geometry and Quantised Responses
In this talk I will talk about non-Abelian band topology and the connection to Riemannian geometry. I will discuss how these ideas culminate in the prediction of quantized shift photoconductivities and show that this response may be recast in terms of the integrated torsion tensor and the non-Abelian Berry connection constituting Chern-Simons forms. Physically, I will motivate that the topological quantization emerges purely from virtual transitions contributing to the optical response and discuss possible generalisations.
-
Xiong-Jun Liu (International Center for Quantum Materials, Peking University):
Quantum Critical States in Quasiperiodic Lattices: From Non-Interacting to Correlated
The disordered quantum systems host three types of fundamental quantum states, the extended, localized, and critical states, of which the multifractal critical states are much less understood compared with the former two. Conventionally the characterization of the quantum critical states relies on arduous numerical verification. In this talk, I will present a systematic analytic and numerical study of the critical states in quasiperiodic systems, with or without particle-particle interactions. Through the Avila global theory, a Fields Medal work which we introduce for the first time to cold atoms, we propose a class of exactly solvable models, dubbed mosaic lattice models, hosting novel types of exact mobility edges separating localized from quantum critical or extended states, With these exactly solvable models, we discover a universal mechanism for the critical states that the such states are due to the vanishing Lyapunov exponent and the incommensurately distributed hopping zeros in the thermodynamic limit, which also serve as a rigorous characterization of the critical states. We further show that in the presence of interactions, the critical states turn into the many-body counterparts upon the finite-size scaling analysis, giving a many-body critical phase, which is an exotic phase in-between the thermal phase and many-body localization. Based on the considerable progresses in spin-orbit coupled optical Raman lattices, which have been widely applied to simulate topological phases, we discuss our latest experimental realization of the present predictions. Future important issues will be commented.
-
Pramod Padmanabhan (Indian Institute of Technology Bhubaneswar):
Braid and Higher Simplex Operators in Integrable Quantum Computing
Two-qubit Yang-Baxter or braiding gates casts quantum computing as a scattering process. Due to the many conserved quantities this procedure is less noisy. Generalising this to 3-and higher-qubit gates relies on solutions to the tetrahedron and higher simplex equations. We will construct such gates systematically using Clifford algebras. The resulting gates are potentially more effective in simulating different quantum algorithms.
-
Po-Yao Chang (National Tsing Hua University in Taiwan):
Entanglement Diagnosis of Many-Body Systems: Applications to Non-Unitary Conformal Field Theory and Topological Quantum Field Theories
Entanglement measures provide powerful tools for diagnosing quantum many-body phases of matter. In particular, in (1+1)-dimensional systems with conformal symmetry, entanglement entropy exhibits logarithmic scaling, where the coefficient determines the central charge of the underlying conformal field theory (CFT). However, in the absence of the unitary condition, the central charge can be negative, leading to negative entanglement entropy. To address this issue, we propose the generalized entanglement entropy to extract the negative central charges in several examples. In addition, in (2+1)-dimensional systems described by topological quantum field theories (TQFT), the sub-leading term of the entanglement entropy is referred to as the topological entanglement entropy (TEE), which contains information about the topological data of the quasiparticles. In this talk, I would like to discuss the TEE for different bipartitions.
-
Tim Byrnes (NYU Shanghai):
Unified Framework for Efficiently Computable Quantum Circuits
Quantum circuits consisting of Clifford and matchgates are two classes of circuits that are known to be efficiently simulatable on a classical computer. We introduce a unified framework that shows in a transparent way the special structure that allows these circuits can be efficiently simulatable. The approach relies on analyzing the operator spread within a network of basis operators during the evolution of quantum circuit. Quantifying the complexity of a calculation by the number of operators with amplitude above a threshold value, we show that there is a generic form of the complexity curve involving an initial exponential growth, saturation, then exponential decay in the presence of decoherence. Our approach is naturally adaptable into a numerical procedure, where errors can be consistently controlled as a function of the complexity of the simulation.
-
Arijeet Pal (University College, London):
Long Range Entanglement in Measurement Induced Phases
In this talk, I will describe two recent applications of tensor networks. In the first part, I will present an efficient technique for quantum process learning, a quintessential primitive to characterize quantum devices. This combines a tensor network representation of the target quantum channel with a data-driven optimization inspired by unsupervised machine learning. These results go far beyond state-of-the-art, providing a practical and timely tool for benchmarking quantum circuits in current and near-term quantum computers. In the second part, in turn, I will briefly describe a recently developed (classical) quantum-inspired algorithm for solving the Navier-Stokes equation in complex geometries, based on tensor trains. This is a full-stack method to solve for incompressible fluids with memory and runtime scaling poly-logarithmically in the mesh size. Our framework is based on matrix-product states (a.k.a tensor trains), a powerful compressed representation of quantum states. It is complete in that it solves for flows around immersed objects of arbitrary geometries, with non-trivial boundary conditions, and self-consistent in that it can retrieve the solution directly from the compressed encoding, i.e. without ever passing through the expensive dense-vector representation. This machinery lays the foundations for a new generation of potentially radically more efficient solvers of real-life fluid problems.
-
Alioscia Hamma (University of Naples Federico II):
Non-stabilizerness in Quantum Mechanics
We all know that entanglement is important in quantum mechanics. However, quantum behavior needs a second ingredient, the so-called non-stabilizerness property, commonly known as magic. Without it, no quantum computer would be able to outperform a classical one, but not only. Quantum chaos would not ensue, and quantum thermodynamics would not be the same. Bell's inequalities would not be violated, and black holes would always be easy to decode. Quantum many-body systems would be boring. Also all the probabilities that come from the Born rule would be trivial. Finally, without non-stabilizerness there would also be no gravity, according to the AdS/CFT conjecture. All these features are captured by the notion of Stabilizer Entropy (SE), which we will introduce and explain in this talk.
-
Markus Müller (RWTH Aachen University, Germany):
The Dawn of Quantum Fault-Tolerance
The construction of scalable fault-tolerant quantum computers remains a fundamental scientific and technological challenge, due to the influence of unavoidable noise. In my talk, I will first introduce basic concepts of quantum error correction, which allows one to protect quantum information during storage and processing. I will in my talk present new theory concepts and recent collaborative experimental advances towards fault-tolerant quantum error correction on various physical quantum computing platforms. Specifically, I will present new fault-tolerance preserving protocols for autonomous quantum error correction [1], which do not require in-sequence measurements of qubits, which are often slow or technically challenging in many state-of-the-art physical quantum processor platforms. I will also show how quantum cellular automata can be designed to give rise to emergent many-body dynamics with quantum error-correcting capabilities [2]. Towards universal fault-tolerant quantum computing with logical qubits — eventually outperforming computations executed on their physical qubit counterparts — I will present new protocols [3] and first experimental demonstrations [4] of fault-tolerant code switching.
[1] S. Heußen et al., Measurement-free fault-tolerant quantum error correction in near-term devices, PRX Quantum 5, 010333 (2024)
[2] T. L. M. Guedes et al., Quantum cellular automata for quantum error correction and density classification, arXiv:2309.03608 (2023)
[3] F. Butt et al., Fault-Tolerant Code Switching Protocols for Near-Term Quantum Processors, arXiv:2306.17686 (2023) [PRX Quantum, in press]
[4] I. Pogorelov, F. Butt et al., Experimental fault-tolerant code switching, arXiv:2403.13732 (2024)
-
Tobias Haug (Quantum Research Center, TII, Abu Dhabi):
Efficient Algorithms for Quantum Magic
Nonstabilizerness or magic characterizes the resources needed to run fault-tolerant quantum computers and is a necessary condition for quantum advantage. The resource theory of magic quantifies the amount of magic in quantum states, which characterizes the cost of preparing states on quantum computers as well as the runtime of a class of classical simulation algorithms. Here, we provide efficient algorithms to quantify magic on quantum computers [1,2] and matrix product states [3,4]. We use these methods to experimentally study the transition from classically simulable stabilizer states into intractable quantum states, and demonstrate their application for state discrimination and certification. Our work also gives novel insight into the magic of critical many-body quantum systems. We reveal that stabilizer entropy, a measure of nonstabilizerness, is in general not extremal even at the critical point. We show that stabilizer entropies can be used to determine the critical point of the transverse field Ising model, and find evidence of magic becoming long-range close to the critical point. Our works open up the exploration of quantum complexity in many-body quantum systems and quantum computers.
-
Chandrashekar Radhakrishnan (NYU Shanghai):
Generalization of Quantum Discord
An important aim of quantum information theory is to understand and quantify the various quantum properties and correlations. This is done by constructing measures and in understanding the operational relevance of information theoretic quantities. The best-known measure of nonclassical correlations is quantum discord [1,2]. In this talk, I will introduce a generalisation of quantum discord to multipartite systems using quantum conditional mutual information [3]. For the tripartite case, we show that the discord can be decomposed into contributions resulting from changes induced by nonclassical correlation breaking measurements in the conditional mutual information and tripartite mutual information. I will also discuss its relation to bipartite nonclassical correlations and monogamy of nonclassical correlations.
-
Elio König (Max Planck Institute for Solid State Research):
Zero Is Not Nothing
The interplay of topological electronic band structures and strong interparticle interactions provides a promising path toward the constructive design of robust, long-range entangled many-body systems. Most recent theories unveil that non-trivial topology is crucially manifested in the zeros of the fermionic Green’s function in Mott insulating systems and demonstrate the occurrence of topological band structures of zeros, and – by bulk-boundary correspondence – of topological edge states of zeros [1]. In this talk, I will spend some time reviewing topological Green’s function zeros and discussing their physical meaning and potential ways to probe them. I will then spend most of the time presenting an exactly soluble local model Hamiltonian [2] based on the Toric Code coupled to fermionic degrees of freedom. I’ll demonstrate the appearance of Green’s function zeros in a non-trivial, integrable limit of the model and employ controlled perturbation theory to demonstrate their topological band structure. I’ll further show that, within this model, Green’s function zeros acquire a finite ‘’lifetime’‘ before the Higgs transition, at which they disappear. The local nature of the model allows us to straightforwardly calculate the quantized Hall response.
[1] N. Wagner, …, EJK, …, G. Sangiovanni, Nat Commun 14, 7531 (2023).
[2] S. Bollmann, C. Setty, U. Seifert, EJK arXiv:2312.14926
-
Aditi Mitra (NYU New York):
Topological Defects in Floquet Circuits
I will discuss how one may construct Floquet models from a fusion category, and how this formalism is a natural way to construct topological defects: non-local operators that can be deformed in the space and time direction without changing the physics. One of these topological defects is the “duality defect” that implements the Kramers-Wannier duality transformation and is a “non-invertible symmetry” as it projects out states of a given parity. I will highlight the consequence of the duality defect on Floquet time-evolution, first for the exactly solvable Floquet-Ising model, and then by adding integrability breaking perturbations to the model.
-
Nadia Boutabba (Institute of Applied Technology, FCHS):
Optically Dense Atomic Systems: From Pulse Shaping to Atomic Localization via Mangneto Optical Rotation
The quantum control of atomic systems can be achieved through the manipulation of their optical properties, i.e the coherence. In EIT systems, a transparency window is achieved via the interference of two laser beams. In this context, our research investigates shaped laser wave-forms to obtain desirable absorption dispersion spectra, controllable refractive index and induces the atomic population inversion. For instance, q-deformed hyperbolic pulse manipulates the system’s dynamic by adjusting the scaling asymmetry factor q of the q-deformed pulse. In addition, the QEXP pulse opens a transparency window in the absorption spectra. In contrast, in the classical scenario where the laser is non-shaped, we control the optical properties of atomic systems via the SGC: spontaneously generated coherence or the MOR.
-
Ken Shiozaki (Yukawa Institute for Theoretical Physics, Kyoto University):
A Discrete Formulation of Three Dimensional Winding Number
For a continuous map from a three-dimensional oriented closed manifold to , the group of by unitary matrices, an integer-valued quantity known as the three-dimensional winding number is defined. We discuss a method to compute the winding number using a discrete approximation of the manifold, ensuring that the result is manifestly quantized. Our approach is a three-dimensional analog of the Fukui-Hatsugai-Suzuki method for calculating the first Chern number.
-
Asif Equbal (NYU AD):
Quantum Vision for Health: Pioneering Light-Activated Spin Sensing
-
Frederico Brito (Quantum Research Center, TII, Abu Dhabi):
Experimental Investigation of Geometric Quantum Speed Limits in Open Quantum Systems
The Quantum Speed Limit (QSL) is a fundamental lower bound on the evolution time for quantum systems undergoing general physical processes and may have important consequences for quantum computing. Here, we study the geometric quantum speed limits of a qubit subject to decoherence in an ensemble of chloroform molecules in a Nuclear Magnetic Resonance experiment. To do so, we controlled the system-reservoir interaction and the spin relaxation rates by adding a paramagnetic salt, which allowed us to observe both Markovian and non-Markovian open system dynamics for the qubit. We used two distinguishability measures of quantum states to assess the speed of the qubit evolution: the quantum Fisher information (QFI) and Wigner-Yanase skew information (WY). We observed crossovers between QSLs related to the QFI and WY metrics for non-Markovian dynamics and low salt concentrations. The WY metric sets the tighter QSL for high concentrations and Markovian dynamics. We also show that QSLs are sensitive even to small fluctuations in spin magnetization.
-
Urs Schreiber (NYU AD):
Towards Certified Topological Quantum Programming via Linear Homotopy Types
Beyond the present NISQ era, useful heavy-duty quantum programs will arguably necessitate (1.) topological quantum circuits for error-protection and (2.) (classical-)computer-verified certificates of correctness — hence essentially a formal verification logic of the underlying topological quantum processes — which may seem a tall order. But we have recently shown that the (conservative) extension of the (programming & certification-)language of “Homotopy Type Theory” (
HoTT) by “linear homotopy types” (LHoTT, for which prototypes exist on paper) namely: by classically-controlled topological quantum data types, naturally lends itself to just this purpose. In this talk I will give an introduction to and survey of this approach to Topological Quantum Programming Certification via Linear Homotopy Types, developed at CQTS @ NYUAD (“Topological Quantum Gates in HoTT” arXiv:2303.02382, “Entanglement of Sections” arXiv:2309.07245, “The Quantum Monadology” arXiv:2310.15735, “Quantum and Reality” arXiv:2311.11035).
Oct 2024
03 Oct 2024
NYU CQTS X QinnovisionQuantum Computing Workshop – PlanQK platform training
Talks:
-
Enrique Solano (Kipu Quantum, Berlin, Germany):
Strategic Overview: Quantum Computing in the next Decade
-
Daniel Voltz:
Quantum Computing in Action: Cutting-Edge Applications for Industry Pioneers
-
Michael Falkenthal:
Advanced Quantum Applications: Real-World Use Cases on Kipu Quantum’s Platform
04 Oct 2024
Quantum Industry Day – Towards Industrial Usefulness with Kipu Quantum
www.q-innovision.com/quantum-industry-day

Nov 2024
19 Nov 2024
Quantum Industry Day – Exploring Quantum Frontiers with IBM Quantum Technology
www.q-innovision.com/quantum-industry-day-november-2024-ibm

23-24 Nov 2024
MENA Quantum Conference 2024
nyuad.nyu.edu/en/events/2024/november/mena-quantum.html

Dec 2024
16 Dec 2024
Quantum Industry Day – IDQUantique
www.q-innovision.com/quantum-industry-day-idq-december

Jan 2025
15 Dec 2025
Quantum Industry Day – Exploring Quantum with Qibo
www.q-innovision.com/quantum-industry-day-january-2025-tii

Feb 2025
28 Feb 2025
Quantum Industry Day Featuring Microsoft
www.q-innovision.com/quantum-industry-day-featuring-microsoft

Apr 2025
17 Apr 2025
Quantum Industry Day
www.q-innovision.com/quantum-industry-day-april-2025

-
27 April 2025
13th Annual International Hackathon
May 2025
-
19-20 May 2025
NYU-NYUAD Workshop on
Quantum Matter and Quantum Computing
nyuad.nyu.edu/en/events/2025/may/quantum-matter-and-quantum-computing.html
joint with Center for Quantum Information Physics, NYU New York
venue: 19 Washington Square North (NYUAD embassy @ NYU New York)
Program:

Monday, May 19:
| Time | Speaker |
|---|---|
| 08:00-08:45 | [Breakfast] |
| 09:00-09:45 | Javad Shabani (NYU) |
| 09:50-10:35 | Meng Cheng (Yale) |
| 10:35-11:00 | [Break] |
| 11:00-11:45 | Sankar Das Sarma (University of Maryland) |
| 11:45-13:00 | [Lunch] |
| 12:00-13:45 | Sophia Economou (Virginia Tech) |
| 13:50-14:35 | Tudor Stanescu (West Virginia) |
| 14:35-15:00 | [Break] |
| 15:00-15:45 | Abhay Pasupathy (Columbia University) |
| 15:50-16:35 | Yi Li (Johns Hopkins University) |
| 16:35-17:00 | [Break] |
| 17:00-18:00 | Chetan Nayak (Microsoft) |
| 18:00 | [Dinner] |
Tuesday, May 20
| Time | Speaker |
|---|---|
| 08:00-08:45 | [Breakfast] |
| 09:00-9:45 | Hisham Sati (NYU Abu Dhabi) |
| 09:50-10:35 | Tim Byrnes (NYU Shanghai) |
| 10:35-11:00 | [Break] |
| 11:00-11:45 | Pouyan Ghaemi (CUNY) |
| 11:45-13:00 | [Lunch] |
| 13:00-13:45 | Emil Prodan (Yeshiva University) |
| 13:50-14:35 | Nicolas Regnault (Princeton University) |
| 14:35-15:00 | [Break] |
| 15:00-15:45 | Urs Schreiber (NYU Abu Dhabi) |
| 15:50-16:35 | Andrei Vrajitoarea (NYU New York) |
| 17:00 | [Closing] |
Group photo:

Titles and materials:
-
Engineering Topological States of Matter
-
Anomalous Insights into Phases of Matter in Open Quantum Systems
-
Majorana Nanowires in Semiconductor/Superconductor Hybrid Platform
-
State preparation for quantum information processing
cf.: arXiv:2411.07920
slides: pdf
-
Planar Josephson junction devices with narrow superconducting strips:
Topological properties and optimizationcf. arXiv:2504.04468
slides: pdf
-
Some thoughts on disorder in superconductors relevant to qubits
-
Novel Unconventional Superconductivity and Phase Sensitive Probes
cf.: arXiv:2407.18701
-
Majorana-Based Topological Qubits
cf.: arXiv:2502.12252
-
Global perspectives on topological quantum matter/information
-
…
-
Quantum algorithm to realize and study fractional Hall states and their dynamics on near term quantum computers: A tabletop experiment on quantum gravity
-
Engineering Topological Dynamics with Operator Algebraic Methods
cf.: arXiv:2406.04226
-
Moiré and more
cf.: arXiv:2502.17320
-
Quantum-controlled Synthetic Matter:
when analog and digitial hybridize
Quantum Colloquium
Weekly colloquium, broadly on quantum systems, with focus on quantum computation and specifically on topological quantum computation and dependently typed quantum programming languages.
May 2022
-
Urs Schreiber on joint work with Hisham Sati:
New Foundations for Topological Data Analysis – The Power of Cohomotopy
The aim of topological data analysis (TDA) is to provide qualitative analysis of large data/parameter sets in a way which is robust against uncertainties and noise. This is accomplished using tools and theorems from the mathematical field of algebraic topology. While a tool called persistent homology has become the signature method of TDA, it tends to produce answers that are either hard to interpret (persistent cycles) or impossible to compute (well groups). Both problems are solved by a variant method FK17 which we may call persistent cohomotopy: A first result shows FKW18 that this new method provides computable answers to the concrete question of detecting whether there exist data+parameters that meet a prescribed target indicator precisely, even in the presence of uncertainty and noise. More generally, efficient data analysis will require further refining persistent cohomotopy to equivariant cohomotopy and/or twisted cohomotopy SS20. Curiously, these flavors of cohomotopy theory have profound relations to formal high energy physics and quantum materials, connecting to which might help to further enhance the power of topological data analysis.
Sep 2022
-
13 Sep 2022
Mitchell Riley (NYU Abu Dhabi, CQTS):
Dependent Type Theories à la Carte
slides: pdf
on realizing linear homotopy type theory
-
14 Sep 2022
Sachin Valera (NYU Abu Dhabi, CQTS):
A Quick Introduction to the Algebraic Theory of Anyons
slides: pdf
on anyon braiding described by braided fusion categories
-
14 Sep 2022
Urs Schreiber (NYU Abu Dhabi, CQTS):
Initial Researchers’ Meeting – Motivation, Strategy & Technology
slides: pdf
outline of a research program on Topological Quantum Programming in TED-K
Oct 2022
-
11 Oct 2022
Tim Byrnes (NYU Shanghai, CQTS):
Topological quantum states for quantum computing and metrology
video: rec
-
Part I – Quantum teleportation of Majorana Zero Modes
slides: pdf
-
Part II – Quantum Hall effect in Bose-Einstein condensates
slides: pdf
on Phys. Rev. A 92.023629 (2015) and Phys. Rev. B 99, 184427 (2019)
-
Nov 2022
-
07 Nov 2022
Jiannis Pachos (Leeds University, UK):
Non-abelian topological Berry-phases
video: rec
Combining physics, mathematics and computer science, topological quantum information [1] is a rapidly expanding field of research focused on the exploration of quantum evolutions that are resilient to errors. In this talk I will present a variety of different topics starting from introducing anyonic models, topological phases of matter, Majorana fermions, characterising knot invariants, their quantum simulation with anyons and finally the possible realisation of anyons in the laboratory.
[1] Jiannis K. Pachos, Introduction to Topological Quantum Computation, Cambridge University Press (2012) doi:10.1017/CBO9780511792908
-
14 Nov 2022
Sachin Valera (NYU Abi Dhabi, CQTS):
A Quick Introduction to the Algebraic Theory of Anyons (Part II)
slides: pdf
on anyon braiding described by braided fusion categories
-
21 Nov 2022
Andrew Kent (Center for Quantum Phenomena, NYU)
A new spin on magnetism with applications in information processing
slides: pdf
Recent advances in magnetism research are likely to have an important impact on electronics and information processing. These advances use the electron magnetic moment (spin) to transmit, write and store information. They enable new devices that operate at high speed with very low energy consumption. The information is stored in the orientation of electron magnetic moments in magnetic materials and can persist without power; energy is only needed to write and read the information. Important physics concepts include the interconversion of electrical (charge) currents into spin currents, the efficiency of the interconversion, controlling the currents, spin polarization direction, and the associated spin torques on magnetic order. Magnetic skyrmions are also of interest both because of their stability — they are topologically protected objects — and because their nucleation and motion can be controlled using spin currents. In this talk I will highlight the new physics concepts that have enabled these advances and discuss some of their applications in information processing.
cf.: J. Appl. Phys. 130 (2021) [doi:10.1063/5.0046950]
-
28 Nov 2022
Asif Equbal (NYU Abu Dhabi, CQTS)
Molecular spin qubits for future quantum technology
slides: pdf
cf.: spin resonance qbits
Spins are a purely quantum mechanical phenomenon and have been proposed as one of the several candidates for qubits in quantum information science. Quantum computers based on spin qubits were first proposed by DiVincenzo, who established five necessary criteria for building a quantum computer. The technology to control the quantum states of nuclear and electron spins and the theory of spin-spin and spin-magnetic field interactions are well developed, but a quantum computer based on spin qubits has not yet been realized. Why is this?
In this talk, I will discuss the challenges in developing spin qubits that meet DiVincenzo’s criteria for quantum computers. First, I will explain in a pedagogical way how to manipulate spins in an external magnetic field that form the building block of quantum logic gates. I will then provide some insight into my own recent research on the development of optically polarized molecular spin qubits in solids.
Dec 2022
-
12 Dec 2022
Quantum Algorithms, from noisy intermediate scale devices through the early fault-tolerant era
Reaching long-term maturity in quantum computation science and technology relies on the field delivering practically useful application in a short term. In this colloquium, I will discuss ideas for the noisy intermediate scale (NISQ) and early fault-tolerant eras. I will divide my talk into two parts. In the first part, I will make a brief non-technical introduction to the field, its relevance to the UAE, and the main lines of research of the Quantum Algorithms division at QRC-TII.
In the second one, I will try to convey some level of technical detail about our work. In particular, I will first present a hybrid classical-quantum algorithm to simulate high-connectivity quantum circuits from low-connectivity ones. This provides a versatile toolbox for both error-mitigation and circuit boosts useful for NISQ computations. Then, I will move on to algorithms for the forthcoming quantum hardware of the early fault-tolerant era: I will present a new generation of high-precision algorithms for simulating quantum imaginary-time evolution (QITE) that are significantly simpler than current schemes based on quantum amplitude amplification (QAA). QITE is central not only to ground-state optimisations but also to partition-function estimation and Gibbs-state sampling, with a plethora of computational applications.
Jan 2023
-
30 Jan 2023
Vivek Singh (CQTS @ NYU Abu Dhabi)
Chern-Simons theory, Knot polynomials & Quivers
slides: pdf
cf. arXiv:2103.10228
First, I will give a brief introduction to knot theory and its connection to Chern-Simons quantum field theory. Then I discuss the method of obtaining polynomial invariants and limitations towards tackling classification of knots. In particular, we will highlight our new results on weaving knots and review the recent developments on Knot-Quiver correspondence.
Feb 2023
-
13 Feb 2023
Kazuki Ikeda (Co-design Center for Quantum Advantage, Stony Brook University, USA)
Demonstration of Quantum Energy Teleportation by Superconducting Quantum Processors and Implications for Communications and High Energy Physics
Quantum energy teleportation is a theoretical concept in quantum physics that describes the transfer of energy from one location to another without the need for a physical medium to carry it. This is made possible by means of universal properties of quantum entanglement and measurement of quantum states. The role of QET in physics and information engineering is largely unexplored, as the theory has not received much attention for long time since it was proposed about 15 years ago. To validate it on a real quantum processor, my research has tested the energy teleportation protocol in its most visible form for the first time on IBM’s superconducting quantum computer. In my colloquium talk, I will explain the historical background of quantum energy teleportation, quantum circuits and quantum operations. Moreover I will present a concrete setup for a long-distance and large-scale quantum energy teleportation with real quantum networks.
In addition, I will present the results of quantum simulations with relativistic field theory as a study based on the high-energy physics perspective and the symmetry-protected topological (SPT) phase of matter of quantum energy teleportation. The models will describe include the two dimensional QED (the massive Thirring model), the AKLT model, the Haldane model, and the Kitaev model. Those results show that the phase diagrams of the field theory and SPT phase are closely related to energy teleportation.
In summary my talk will provide a novel suggestion that quantum energy teleportation paves a new pathway to a link between quantum communication on real quantum network, phase diagram of quantum many-body system, and quantum computation.
-
20 Feb 2023
Constructive Real Numbers in the Agda Proof Assistant
cf. arXiv:2205.08354
Proof assistant software enables the development of proofs in a manner such that a computer can verify their validity. As proof assistants commonly take the form of a programming language, users face programming-related problems, such as the naturality of expressing ideas and algorithms in the language, usability, and performance. We will investigate these issues as they occur in developing Errett Bishop’s constructive real numbers in the Agda proof assistant and functional programming language, with an introduction to each.
-
27 Feb 2023
Aeysha Khalique (National University of Science and Technology, Islamabad):
Computational Tasks through Non-Universal Quantum Computation
video: YT
Quantum Mechanics offers phenomena which defy our everyday observation. These are not just theoretical principles but have wide range applications in quantum computation and quantum information, making some tasks possible which are impossible to be done classically. This talk will take you to the journey through quantum computation, starting from underlying principles to the applications, including my own own contribution to it.
Mar 2023
-
6 Mar 2023
Altaf Nizamani and Qirat Iqbal (University of Sindh, Pakistan):
Quantum Technology with Trapped Ions
video: YT
Quantum technology is a rapidly advancing field that is poised to revolutionize numerous industries, including computing, communications, sensing, and cryptography. At its core, quantum technology relies on the principles of quantum mechanics, which allow for the creation of devices that operate on the quantum level. These devices based on quantum technology can perform tasks that are impossible or prohibitively difficult for classical devices. One of the most promising applications of quantum technology is in quantum computing, quantum communications, and quantum sensors.
Trapped ions are one of the promising platform for quantum computing and sensing. In this approach, individual ions are trapped in a vacuum chamber using electromagnetic fields and manipulated using lasers to perform quantum operations. As a quantum system, trapped ions offer several advantages. First, they have long coherence times, meaning that the quantum state of the ion can be preserved for a longer period, allowing for more complex calculations. Second, trapped ions can be precisely controlled and manipulated, allowing for the implementation of high-fidelity quantum gates. Finally, trapped ions can be entangled with one another, allowing for the implementation of quantum algorithms that are impossible to simulate on classical computers. Trapped ions also have great potential as quantum sensors. By using the properties of the ions to measure changes in their environment, trapped ions can detect minute changes in temperature, magnetic fields, and electric fields, among other things. This makes them useful for applications in precision measurement, such as in atomic clocks, gravitational wave detection, and magnetometry.
One of the major challenges facing trapped ion systems is scalability. While individual ions have been used to perform simple quantum algorithms, scaling the system up to include a large number of ions is a difficult task. However, recent advances in ion trap technology have made it possible to trap larger numbers of ions and transport them in 2D and 3D space to perform more complex operations for quantum computation and sensing experiments. Realization of such devices is not far away. As compared to present atomic clocks, a new generation of quantum-enhanced clocks is now emerging showing significantly improved accuracy. Sensitive physical measurements are an essential component of modern science and technology. Developments in quantum sensors will outdate their classical counterparts.
We will present recent developments and opportunities in quantum technology applications based on trapped ions, including quantum computation and sensing.
-
13 Mar 2023
Roger S. K. Mong (Pittsburgh Quantum Institute, USA)
Detecting topological order from modular transformations of ground states on the torus
cf.: arXiv:2203.04329
Every two-dimensional topological phase is associated with some topological quantum field theory (TQFT), or more formally a modular tensor category. The ground states of a topological phase encode information about the TQFT, which makes them useful in determining the TQFT data, such as anyon mutual statistics and self statistics. For example, many numerical methods for detecting the TQFT relied on the use of minimum entanglement states (MESs), which are the eigenstates of the Wilson loop operators, and are labeled by the anyons corresponding to their eigenvalues. Here we revisit the definition of the Wilson loop operators and MESs. We rederive the modular transformation of the ground states purely from the Wilson loop algebra, and as a result, the modular - and -matrices naturally show up in the overlap of MESs. Importantly, we show that due to the phase degree of freedom of the Wilson loop operators, the MES-anyon assignment is not unique. This ambiguity means that there are some sets of TQFTs that cannot be distinguished from one another solely by the overlap of MESs.
-
27 Mar 2023
Matthias Christandl (Centre for the Mathematics of Quantum Theory, U. Copenhagen):
Quantum Software
cf.: arXiv:2009.07161 doi:10.1109/TIT.2022.3169438
In these days, we are witnessing amazing progress in both the variety and quality of platforms for quantum computation and quantum communication. Since algorithms and communication protocols designed for traditional ‘classical’ hardware do not employ the superposition principle and thus provide no gain even when used on quantum hardware, we are in need of developing specific quantum algorithms and quantum communication protocols that make clever use of the superposition principle and extract a quantum advantage. “Quantum hardware needs quantum software”, so to say. Furthermore, due to noise in the qubits, known as decoherence, an additional quantum-specific software layer is required that emulates a perfect quantum machine on top of a noisy one. I will demonstrate our recent work on this subject with theorems as well data from university and commercial quantum devices.
Apr 2023
-
3 Apr 2023
Mouzhe Xie (University of Chicago)
Diamond-based quantum sensor for molecular analytics
cf.: arXiv:2108.04843
slides: pdf
video: YT
Quantum sensing technologies enable some of the most precise measurements that human beings have ever achieved. In recent years, optically addressable nitrogen-vacancy (NV) color center hosted by diamond crystal has been used as a novel quantum sensor, which has exquisitely sensitive response to local magnetic field fluctuations. It is therefore capable to perform micro-/nano-scale NMR experiments, manifesting enormous potential to study biological systems on extremely small sample volume – even down to single-molecule regime.
In this seminar, I will discuss some of the comprehensive efforts to develop NV-based quantum sensing platforms for a wide range of applications in chemistry and biology. I will start with a general introduction to quantum sensing followed by conventional NMR spectroscopy as a powerful tool to study biomolecules, as well as their connections to the NV-based nanoscale NMR. I will then introduce a biocompatible surface functionalization architecture for interfacing a diamond quantum sensor with individual intact biomolecules under physiological conditions. A sensing modality based on diamond membrane integrated with flow channel will also be discussed, which is a promising platform for a variety of experiments a molecular, cellular, and even living-organism levels. Finally, I will conclude by providing an outlook on how NV-based quantum sensing platforms, combined with other advanced spectroscopy and microscopy methods, can be utilized to address important biophysical and bioanalytical questions with unprecedented sensitivity and spatial resolution, which will enhance our understanding of molecular interactions and cellular processes and ultimately improve human health.
-
3 Apr 2023
Sophia Economou (Center for Quantum Information Science and Engineering, Virginia Tech, USA)
Control and distribution of entanglement in quantum networks
cf.: arXiv:2212.10820
video: YT
Quantum networks are pursued as a quantum backbone on which to perform secure quantum communication, distributed quantum sensing, and blind quantum computation. The building blocks of these networks are quantum repeaters, where photonic quantum information carriers are generated and error corrected through interactions with matter qubits. I will describe two paradigms of quantum repeaters and discuss in each case how careful control of a register of spin qubits can increase the entanglement distribution rate over the network. Specifically, I will describe our recent work on the accurate and fast control of nuclear spin memory qubits coupled to spin defects such as the NV center in diamond. I will also discuss the deterministic generation of photonic ‘graph“ states from such quantum emitters.
-
10 Apr 2023
Zain Saleem (Argonne National Lab, USA)
Classical simulators as quantum error mitigators via circuit cutting
cf.: arXiv:2212.07335
video: YT
We introduce an error mitigation framework that mitigates errors in a quantum circuit using circuit cutting. Our framework can be implemented in polynomial time for a wide variety of quantum circuits. Our technique involves cutting the circuit in such a way that we run the circuit that needs to be executed on the quantum hardware whereas the error mitigation circuit is run on a simulator. We perform error mitigation qubit by qubit and then provide a way to combine the different probabilities from each of the individual qubit error mitigation runs such that the full circuit is error mitigated. We apply our framework to the VQE hardware-efficient ansatz acheiving estimated ground state energies very close to the noise-free simulation results.
-
17 Apr 2023
Piotr Sułkowski (University of Warsaw, Poland)
Knots-quivers correspondence: summary and update
cf. arXivL2110.13768 following arXiv:1707.04017, arXiv:1707.02991
In this talk I will review the knots-quivers correspondence and mention some recent developments in this regard. The knots-quivers correspondence is the statement that various invariants associated to a knot are encoded in the corresponding quiver. This statement follows from engineering both knots and quivers in related brane systems in string theory. Recent developements, which I will mention at least briefly, include understanding the structure of various quivers that correspond to the same knot, using topological recursion to determine quiver generating series and corresponding quiver A-polynomials, and finding a quiver representation of so-called Z-hat invariants.
-
24 Apr 2023
Mauro Paternostro (Queen’s University Belfast, Ireland):
Alice through the looking glass: cavity optomechanics for the study of the foundation of quantum mechanics
cf.: arXiv:2302.08995
I will illustrate how cavity optomechanics is helping us addressing deep questions on our understanding of the foundations of quantum theory, from non-equilibrium quantum dynamics to the collapse of the wave-function. Towards the end of my talk, I will propose an optomechanical pathway for the exploration of the potential quantum nature of gravity.
May 2023
-
1 May 2023
Hichem El Euch (American University of Sharjah, UAE):
High-fidelity universal quantum computation with symmetric qubit clusters
Designing a physical device that maintains the error rate for each quantum processing operation low is one of the most arduous issues for the implementation of a scalable quantum computer. These errors may result from inaccurate quantum manipulation, such as a gate voltage sweeping in solid-state qubits or a laser pulse duration. Decoherence is usually a manifestation of the interaction with the environment, and it is an entity of the quantum system which generates errors. Small clusters of qubits with symmetries can be used to shield part of them from decoherence. We encode pairs of connected qubits and universal 2-qubit logical gates using 4-level cores with omega-rotation invariance. We show that symmetry renders logical operations particularly resistant to anisotropic qubit rotations that models some quantum errors. We suggest a scalable method for universal quantum processing in which cores act as quansistors, or quantum transistors. By adjusting their intrinsic variables, quansistors may be dynamically isolated from their environment, providing them the adaptability needed to function as controlled quantum memory units.
-
8 May 2023
Ilya Kuprov (University of Southampton):
Optimal control of large spin systems
cf.: arXiv:2107.00933, arXiv:2303.09458
video: YT
In magnetic resonance, optimal control theory is used to generate pulses and pulse sequences that achieve instrumentally difficult objectives (for example, uniform 13C excitation in a 1.2 GHz magnet) with high precision under stringent time and radiofrequency/microwave power constraints. At the moment, the most popular framework is GRAPE (gradient ascent pulse engineering, 10.1016/j.jmr.2004.11.004). This lecture reports our recent mathematical and software engineering work on the various extensions and refinements of the GRAPE framework, and on its implementation as a module of Spinach library. Recently implemented functionality includes: fidelity Hessians and regularised Newton-Raphson optimisation, generalised curvilinear waveform parametrisation, prefix and suffix pulse sequences, multi-target and subspace control, keyhole states and subspaces, cooperative pulses and phase cycles, and piecewise-linear control sequences. In keeping with the long tradition, the methods are also directly applicable to quantum technologies outside Magnetic Resonance.
Sep 2023
-
25 Sep 2023
Urs Schreiber (NYUAD, CQTS)
Quantum Channels as QuantumState Monad Transformations (Part I)
cf.: arXiv:2310.15735
The talk recalls some of the theory of “quantum channels” and then explains how this is captured by “monadic computation” with the linear version of the “State monad” – the “QuantumState Frobenius monad”.
Oct 2023
-
2 Oct 2023
Titus Neupert (University of Zurich)
Realizing Higher-Order Topology
video: Zm
cf. doi:10.1126/sciadv.aat0346
Higher-order topology generalizes the bulk-boundary correspondence of topological phases of matter, by allowing topological modes to be localized at corners and hinges instead of edges and surfaces. I will introduce the theory behind this concept, both for noninteracting as well as interacting systems and consecutively discuss two realizations in rather distinct setups. First, as-grown crystals of bismuth, grey arsenic, as well as bismuth bromide are demonstrated to display the essential physics of higher-order topological insulators. Second, it is shown that lattices of so-called Shiba bound states induced by magnetic adatoms in conventional superconductors can be brought into a higher-order superconducting phase. I will report on experimental progress for both system types based on spanning probe as well as transport measurements.
-
9 Oct 2023
Sachin Valera (NYUAD, CQTS)
Topological Quantum Teleportation Without Braiding
cf. arXiv:2303.17700
We present the quantum teleportation and superdense coding protocols in the context of topological qudits, as realised by anyons. The simplicity of our proposed realisation hinges on the monoidal structure of Tambara-Yamagami categories, which readily allows for the generation of maximally entangled qudits. In particular, we remove the necessity for the braiding of anyons, an operation which typically underpins any computation. Both protocols find a natural interpretation in the graphical calculus for these categories.
-
16 Oct 2023
Anne Broadbent (University of Ottowa, Canada)
Quantum Delegation with an Off-the-Shelf Device
video: Zm
cf. arXiv:2304.03448
Given that reliable cloud quantum computers are becoming closer to reality, the concept of delegation of quantum computations and its verifiability is of central interest. Many models have been proposed, each with specific strengths and weaknesses. Here, we put forth a new model where the client trusts only its classical processing, makes no computational assumptions, and interacts with a quantum server in a single round. In addition, during a set-up phase, the client specifies the size of the computation and receives an untrusted, off-the-shelf (OTS) quantum device that is used to report the outcome of a single constant-sized measurement from a predetermined logarithmic-sized input. In the OTS model, we thus picture that a single quantum server does the bulk of the computations, while the OTS device is used as an untrusted and generic verification device, all in a single round. In this talk, we will show how the delegation of quantum computations can be achieved in the OTS model, and furthermore how to make this protocol zero-knowledge. The emphasis will be on the concepts that contribute to this result; these concepts are drawn from a long line of research related to blind and delegated quantum computation, as well as quantum zero-knowledge proofs. Based on joint work with Arthur Mehta and Yuming Zhao.
-
23 Oct 2023
Frank (Peng) Fu (Univ. Soth Carolina):
Proto-Quipper with Dynamic Lifting
Quipper is a functional programming language for quantum computing. Proto-Quipper is a family of languages aiming to provide a formal foundation for Quipper. By virtue of being a circuit description language, Proto-Quipper has two separate runtimes: circuit generation time and circuit execution time. Values that are known at circuit generation time are called parameters, and values that are known at circuit execution time are called states. Dynamic lifting is an operation that enables a state, such as the result of a measurement, to be lifted to a parameter, where it can influence the generation of the next portion of the circuit. As a result, dynamic lifting enables Proto-Quipper programs to interleave classical and quantum computation. In his talk, Dr. Frank will describe how to extend Proto-Quipper-M with dynamic lifting. He will explain the syntax of a language named Proto-Quipper-Dyn. Its type system uses a system of modalities to keep track of the use of dynamic lifting. Then, he will discuss the categorical semantics for dynamic lifting. Finally, if time permits, Dr. Frank will give some examples of Proto-Quipper-Dyn programs.
-
30 Oct 2023
Dominik Bucher (Technical University, Munich):
Quantum Sensing with Spin Defects in Diamond
cf.: arXiv:2306.07593
The nitrogen-vacancy (NV) point defect in diamond has emerged as a new class of quantum sensors. The technique is based on optically detected magnetic resonance of the NV electronic spins, which can be used to detect magnetic fields on unprecedented length scales. In my talk, I will briefly introduce the basics of NV-based quantum sensing, its hardware and review recent highlights in the field. In the second part, I will discuss recent developments in my research group, including quantum sensing in microfluidics for lab-on-a-chip applications and an outlook for single-cell NMR metabolomics.
Nov 2023
-
06 Nov 2023
Alberto Marchisio (NYUAD):
Quantum Machine Learning: Current Trends, Challenges, Opportunities, and the Road Ahead
video: Zm
cf. arXiv:2310.10315
Quantum Computing (QC) claims to improve the efficiency of solving complex problems, compared to classical computing. When QC is applied to Machine Learning (ML) applications, it forms a Quantum Machine Learning (QML) system. After discussing the basic concepts of QC and its advantages over classical computing, this talk reviews the key aspects of QML in a comprehensive manner. We discuss different QML algorithms and their domain applicability, quantum datasets, hardware technologies, software tools, simulators, and applications. Valuable information and resources are provided to jumpstart into the current state-of-the-art techniques in the QML field.
Dec 2023
-
05 Dec 2023
Javad Shabani (Center of Quantum Information Physics, NYU):
Towards Realization of Protected Qubits Using Topological Superconductivity
video: Zm
cf.: arXiv:2303.04784, arXiv:2101.09272
A central goal in quantum computing research is to protect and control quantum information from noise. This talk will provide recent progress on the developing field of topological superconductivity where we can encode information in spatially separated Majorana zero modes (MZM). We show that topological superconductivity can be achieved in certain hybrid materials where the topological properties are not found in the constituent materials. These special MZMs are formed at the location of topological defects (e.g. boundaries, domain walls,..) and manifest non-Abelian braiding statistics that can be used in noise-free unitary gate operations. We show by engineering a reconfigurable domain wall on a Josephson junction we can create a scalable platform to study MZM properties and their applications in quantum information science.
-
11 Dec 2023
Chandrasekhar Ramanathan (Dartmouth College, New Hampshire):
Quieting Noisy Neighbors: Extending the Coherence Times of Central Electronic Spins in Solids
video: YT
Isolated electronic spins such as donors in silicon and defects like the nitrogen-vacancy (NV) center in diamond are promising platforms for some quantum technologies. The decoherence of these spins is often dominated by interactions with other electronic or nuclear spin species present in their vicinity. For example, silicon-29 nuclear spins can limit the coherence times of donors in silicon, and substitutional nitrogen or P1 centers often limit the coherence times of NV centers in diamond. In this talk I will describe two recent sets of experiments from our group where we are able to extend the coherence times of the central spin by engineering these spin-bath interactions. First, I show how the coherence times of phosphorus donors in silicon are influenced by low-power above-bandgap optical excitation. Next, I describe the use of dynamical decoupling techniques to suppress NV-P1 interactions in diamond. In addition to extending coherence times, these decoupling techniques can be used to measure time-dependent magnetic fields, a form of AC-sensing or noise spectroscopy.
Jan 2024
-
22 Jan 2024
Matteo Capucci (University of Strathclyde):
Para Construction as a Wreath Product
slides: pdf
cf. arXiv:2105.06332
on the para construction in categorical systems theory
-
28 Jan 2024
Alessandra Di Pierro (University of Verona):
Topological Kernels via Quantum Computation
cf. arXiv:2307.07383
Topological data analysis (TDA) enhances the analysis of objects by embedding them into a simplicial complex and extracting useful global properties such as the Betti numbers, i.e. the number of multidimensional holes, which can be used to define kernel methods that are easily integrated with existing machine-learning algorithms. These kernel methods have found broad applications, as they rely on powerful mathematical frameworks which provide theoretical guarantees on their performance. However, the computation of higher-dimensional Betti numbers can be prohibitively expensive on classical hardware, whereas quantum algorithms can approximate them in polynomial time in the instance size. In this work, we propose a quantum approach to defining topological kernels that is based on constructing Betti curves, i.e. topological fingerprint of filtrations with increasing order.
Feb 2024
-
05 Feb 2024
Catalytic Embeddings: Theory and Applications
cf.: arXiv:2305.07720
video: kt
Let be a quantum circuit and let be a set of quantum gates. A catalytic embedding of over is a pair consisting of a state and a circuit over such that for every state we have . Because the state is left unchanged by the application of , it is known as a catalyst. Catalytic embeddings are useful when the circuit cannot be exactly represented over the gate set . In such cases, one can leverage the catalyst to implement (any number of occurrences of) using circuits over .
In this talk, I will present the theory of catalytic embeddings and discuss applications to the exact and approximate synthesis of quantum circuits.
-
12 Feb 2025
Chandrashekar Radhakrishnan (NYU Shanghai):
Theory of Quantum Coherence and Its Application in Quantum Synchronization
video: Zoom
Coherence is a well-known feature of quantum systems. An information theoretic investigation of quantum coherence was initiated in [1] from a resource theory perspective. In this talk, I will provide an outline of quantifying coherence, the two different forms corresponding to it namely the intrinsic coherence and local coherence, and trade-off relation between these two types of coherence [2]. As an application, I will talk about the role of quantum coherence in the study of quantum synchronization. First, I will give an overview of synchronization. Then considering an open quantum system comprising of a two-level system interacting with an external environment, I will show how it exhibits phase preference in the long-time limit. While this phase preference, which we identify as quantum phase localization, shows features like Arnold tongue, which is considered as an identifier for quantum synchronization, I present evidence to show that it is not quantum synchronization [3]. Finally, I will discuss the challenges remaining to be addressed in connecting these two related phenomena of quantum phase localization and quantum synchronization.
References:
- T. Baumgratz, M. Cramer, M. B. Plenio, Quantifying Coherence, Phys. Rev. Lett. 113 140401 (2014) [arXiv:1311.0275, doi:10.1103/PhysRevLett.113.140401]
- R. Chandrashekar, P. Manikandan, J. Segar, Tim Byrnes, Distribution of quantum coherence in multipartite systems, Phys. Rev. Lett. 116 150504 (2016) [arXiv:1602.00286, doi:10.1103/PhysRevLett.116.150504]
- Md. Manirul Ali, Po-Wen Chen, R. Chandrashekar, Physica A 633, 129436 (2024) [doi:10.1016/j.physa.2023.129436]
-
19 Feb 2024
Venkata SubbaRao Redrouthu (NYU AD):
The Quantum Symphony: Electron Spin Choreography for Hyperpolarized Nuclear Spin Sensing
Delving into the atomic secrets encoded within nuclear spins necessitates a quantum leap in sensitivity. My research endeavors to achieve this leap through Pulsed Dynamic Nuclear Polarization (DNP), an emerging technique that harnesses quantum-controlled electron spins to hyperpolarize nuclear spins, overcoming inherent sensitivity challenges in Nuclear Magnetic Resonance (NMR) spectroscopy.
In this presentation, I demonstrate a novel quantum mechanical scheme: broad-band pulsed DNP sequences. Comprising carefully choreographed sequences of quantum gates or pulses, each precisely controlled in phase and time, these sequences represent a pivotal advancement beyond conventional DNP methods. Through density matrix-based theoretical analyses and numerical simulations, I navigate the intricacies of these sequences, offering a deeper comprehension of their foundational principles and the quantum symphony they orchestrate in enhancing nuclear spin sensitivity.
-
26 Feb 2024
Reversible and Quantum Control-Flow
cf. arXiv:1804.00952
One perspective on quantum algorithms is that they are classical algorithms having access to a special kind of memory with exotic properties. This perspective suggests that, even in the case of quantum algorithms, the control flow notions of sequencing, conditionals, loops, and recursion are entirely classical. There is, however, another notion of execution control flow that is itself quantum. In this talk, we shall overview the two paradigms and discuss the issues specific to quantum control.
Mar 2024
-
08 Mar 2024
Hayder Salman (University of East Anglia):
Dynamics of a Nonequilibrium Discontinuous Quantum Phase Transition in a Spinor Bose-Einstein Condensate
cf. arXiv:2312.16555
video: Zoom
Symmetry-breakingquantum phase transitions lead to the production of topological defects or domain walls in a wide range of physical systems. In second-order transitions, these exhibit universal scaling laws described by the Kibble-Zurek mechanism, but for first-order transitions a similarly universal approach is still lacking. Here we propose a spinor Bose-Einstein condensate as a testbed system where critical scaling behavior in a first-order quantum phase transition can be understood from generic properties. We generalize the Kibble-Zurek mechanism to determine the critical exponents for: (1) the onset of the decay of the metastable state on short times scales, and (2) the number of resulting phase-separated ferromagnetic domains at longer times, as a one-dimensional spin-1 condensate is ramped across a first-order quantum phase transition. The predictions are in excellent agreement with mean-field numerical simulations and provide a paradigm for studying the decay of metastable states in experimentally accessible systems.
-
25 Mar 2024
Kapil Kumar:
Realization and Characterization of Topological Materials
Topological insulators (TIs) have emerged as a fascinating class of materials with unique electronic properties driven by non-trivial topology. Their exotic behavior, such as robust metallic states on the surface while being insulating in the bulk, has attracted significant attention from both theoretical and experimental communities. Characterizing these materials accurately is crucial for understanding their fundamental properties and exploring potential applications in quantum computing, spintronics, and topological quantum devices.
This abstract provides an overview of the characterization techniques employed in the study of topological insulators. We discuss both experimental and theoretical approaches utilized to probe their electronic structure, surface states, topological invariants, and transport properties. Experimental techniques encompass a wide range of methods, including angle-resolved photoemission spectroscopy (ARPES), scanning tunneling microscopy/spectroscopy (STM/STS), magneto-transport measurements, and optical spectroscopy. These techniques provide invaluable insights into the band structure, Fermi surface topology, surface states, and the presence of any exotic quantum phenomena.
On the theoretical front, available various computational methods, such as density functional theory (DFT), tight-binding models, and topological indices, play a pivotal role in predicting and understanding the topological properties of these materials. These theoretical approaches not only aid in interpreting experimental results but also guide the design of novel topological materials with tailored properties.
Apr 2024
-
15 Apr 2024
Elisa Ercolessi (University of Bologna, Italy):
Hybrid Variational Algorithms on a Neutral Atom Platform
Quantum Computing is seen as a potential breakthrough for the study of hard classical problems as well as for quantum many body systems. However, we are in the era of NISQ devices and still far away from fault-tolerant machines.
This leads us to consider the possibility of hybrid classical-quantum protocols of variational type: they exploit quantum resources to efficiently prepare states that depend on a suitable chosen set of variational parameters, which can then be determined by means of optimization algorithms to be run on a classical computer. The choice of such classical optimizer schemes is to be guided by compatibility requirements with respect to current available quantum platforms.
To evaluate the feasibility of such an approach, we present an application of the Quantum Approximate Optimization Algorithm to a typical classical hard combinatorial problem, that has been emulated and tested on a real Rydberg atom quantum machine.
May 2024
-
06 May 2024
Roberto Zucchini (University of Bologna, Italy):
A New Quantum Computational Setup for Algebraic Topology via Simplicial Sets
slides: pdf
video: kt
cf.: arXiv:2309.11304
We present a quantum computational framework for algebraic topology based on simplicial set theory extending existing approaches limited to simplicial complexes and aimed mostly to topological data analysis. The proposed set-up applies to any parafinite simplicial set and proceeds by associating with it a finite dimensional simplicial Hilbert space, whose operator structure is analyzed. We show in particular how the problem of determining the simplicial set's homology can be solved within the simplicial Hilbert framework. We examine further the conditions under which simplicial set theoretic algorithms can be implemented in a quantum computational setting taking into account a quantum computer‘s finite resources and outline finally a quantum algorithmic scheme capable to compute the simplicial homology spaces and Betti numbers of a simplicial set combining a number of basic quantum algorithms.
Sep 2024
-
02 Sep 2024
Nouhaila Innan (CQTS, NYUAD):
Quantum Machine Learning for Advanced AI: Development and Application Across Diverse Domains
As the demand for more sophisticated computational tools grows, Quantum Machine Learning (QML) emerges as a potential solution, combining the strengths of Machine Learning (ML) and Quantum Computing (QC) to push the boundaries of what is computationally possible. This exploration takes a deep dive into advanced QML models, such as quantum neural networks, and provides an extensive overview of fundamental data encoding techniques essential for translating classical data into quantum states. Building on these foundational elements, Quantum Federated Learning (QFL) is introduced as a novel approach that enhances privacy and security in decentralized systems by integrating federated learning with quantum principles. The discussion also covers potential applications in finance and cybersecurity, showcasing the significant impact QML could have on these sectors. This talk highlights the considerable potential of QML as a key enabler of advanced artificial intelligence, emphasizing its role in driving innovation across various domains.
-
09 Sep 2024
Sajith Sadasivan (CQTS, NYUAD)
Role of Quantum Coherences in Integrated Solid Effect DNP
Quantum sensing using magnetic resonance techniques, such as Nuclear Magnetic Resonance (NMR), Magnetic Resonance Imaging (MRI), etc. utilizes the quantum properties of the nuclear spins to explore the structural and dynamical characteristics of molecules. This makes it a powerful tool for materials science, biomedical, and quantum technology applications. However, these techniques suffer from an inherent low signal sensitivity. A hyperpolarization method known as Dynamic Nuclear Polarization (DNP) enhances the sensitivity of NMR and MRI by transferring polarization from electron spins to nuclear spins. The traditional DNP methods face challenges in efficiently polarizing systems with broad Electron Paramagnetic Resonance (EPR) lines. To overcome this limitation, Integrated Solid Effect (ISE) DNP is widely used for improved polarization transfer efficiency. Despite its broad application, the role of quantum coherences in ISE DNP remains poorly understood. The quantum coherences generated during electron-nucleus Double-Quantum (DQ) and Zero-Quantum (ZQ) transitions are crucial for maximizing DNP efficiency. Using density matrix formalism, we provide a detailed analysis of quantum coherences in the ZQ and DQ subspaces, as well as the electron’s Single-Quantum (SQ) basis, revealing their impact on ISE DNP. Our findings offer new insights into utilizing room-temperature hyperpolarization in biomedical applications.
-
23 Sep 2024
Urs Schreiber (NYU AD, CQTS):
Abelian Anyons on Flux-Quantized M5-Branes
cf.: arXiv:2408.11896
While fractional quantum Hall systems provide the best experimental evidence yet of (abelian) anyons plausibly necessary for future fault-tolerant quantum computation, like all strongly-coupled quantum systems their physics is not deeply understood. But, generally a promising approach is to (holographically) realize such systems on branes in string/M-theory; and specifically an old argument by Hellerman & Susskind gives a sketch of fractional quantum Hall states arising via discrete light cone quantization of M5/M9-brane intersections.
In this talk I survey (following arXiv:2408.11896) a rigorous derivation of abelian anyon quantum states on M5MO9-branes (“open M5-branes”) on the discrete light cone, after globally completing the traditional local field content on the M5-worldvolume via a flux-quantization law compatible with the ambient 11d supergravity, specifically taken to be in unstable co-Homotopy cohomology (“Hypothesis H”).
The main step in the proof uses a theorem of Okuyama to identify co-Homotopy moduli spaces with configuration spaces of strings with charged endpoints, and identifies their loop spaces with cobordism of framed links that, under topological light cone quantization, turn out to be identified with the regularized Wilson loops of abelian Chern-Simons theory.
-
30 Sep 2024
Vladimir Korepin (Stony Brook University, USA):
Lessons of Many-Body Quantum Mechanics for Circuit Design
cf. arXiv:2406.08320
slides: pdf
Brick-wall circuits composed of the Yang-Baxter gates are integrable. It becomes an important tool to study the quantum many-body system out of equilibrium. To put the Yang-Baxter gate on the quantum computer, it has to be decomposed into the native gates of quantum computers. It is favorable to apply the least number of native two-qubit gates to construct the Yang-Baxter gate. We study the geometric representations of all -type braid gates and their corresponding Yang-Baxter gates via the Yang-Baxterization. We find that the braid and Yang-Baxter gates can only exist on certain edges and faces of the two-qubit tetrahedron. We identify the parameters by which the braid and Yang-Baxter gates are the Clifford gate, the matchgate, and the dual-unitary gate. The geometric representations provide the optimal decompositions of the braid and Yang-Baxter gates in terms of other two-qubit gates. We also find that the entangling powers of the Yang-Baxter gates are determined by the spectral parameters. Our results provide the necessary conditions to construct the braid and Yang-Baxter gates on quantum computers.
Oct 2024
-
21 Oct 2024
Sheng-Jie Huang (Oxford University and Max Planck Institute for the Physics of Complex Systems):
Quantum Matter Through the Lens of Topological Holography
cf. arXiv:2405.09611
It is well known that symmetry offers valuable insights for organizing quantum phases of matter and leads to important physical consequences, such as [conservation laws]] and constraints on the low-energy dynamics of a quantum field theory.
Recently, significant progress has been made in generalizing the concept of symmetry and exploring its connection to topological defects. In this talk, I will introduce a holographic principle for generalized symmetries, referred to as topological holography, which describes the generalized symmetry of a quantum system in terms of a topological order in one higher dimension.
This framework decouples the topological data from the local dynamics of the theory and provides a unified description of symmetry and duality in both gapped and gapless phases of matter. Specifically, I will focus on various exotic quantum critical points and gapless phases in (1+1)d, including phase transitions between symmetry-protected topological (SPT) phases, symmetry-enriched quantum critical points, deconfined quantum critical points, and intrinsically gapless SPT phases.
-
22 Oct 2024
Phani Kumar Peddibhotla (Indian Institute of Science Education and Research, Bhopal, India):
Quantum Sensing Using NV Centers in Diamond
cf.: arXiv:1612.05325
Diamond serves as an ideal crystalline host for a variety of point defects due to its exceptional qualities such as wide band gap, small spin-orbit coupling, and its availability in high-quality, isotopically purified single crystals. Among the possible defects, the nitrogen-vacancy (NV) defect, which is an optically active paramagnetic defect, has been extensively studied as its spin state can be optically initialized and measured at room temperature, and can be manipulated via electron spin resonance by microwave radiation.
Owing to its unique properties, the NV center in diamond has been used to measure a number of physical quantities such as magnetic field, electric field, temperature, and stress/strain at ambient conditions [1, 2]. Consequently, NV quantum sensors have not only enabled the measurement of magnetic resonance from a single electron spin and a few nuclear spins [1], but also emerged as a spectroscopic tool for imaging the charge and strain environments intrinsic to the diamond lattice [3,4].
In this talk, I’ll discuss our recent work on utilizing NV sensors for high-sensitivity scalar, vector, and zero-field magnetometry applications.
References:
1. R. Schirhagl et al, Annual Reviews in Physical Chemistry, 2014, 65, 83.
2. P. Peddibhotla et al, Nano Letters, 2017, 17 (3), 1496
3. T. Mittiga et al, Phys. Rev. Lett. 121, 246402 (2018).
4. S. Kumar et al, 2023 Quantum Sci. Technol. 8 025011
Nov 2024
-
04 Nov 2024
Edison Murairi (Fermi National Accelerator Laboratory (Fermilab)):
Simulating QCD on Quantum Computers
cf.: arXiv:2208.11789
Despite significant progress in the last decades, numerical simulations of QCD on classical computers encounter significant challenges. For example, the Hilbert space grows exponentially with the degrees of freedom, and Monte Carlo simulations of lattice QCD suffer from the sign problem at finite fermion density. Quantum computers are promising candidates to study QCD non-perturbatively. However, simulating QCD on a quantum computer requires digitizing infinite-dimensional gluon fields, while minimizing the number of qubits (or qudits). Moreover, the digitization scheme must also support efficient quantum circuits to perform time evolutions and compute quantities of interest. Several digitization schemes have been proposed recently. In this talk, I will present the method of finite discrete groups, and analysis of its qubits and quantum circuits cost.
-
11 Nov 2024
Arthur Parzygnat (MIT, USA):
A Spatiotemporal Extension of Density Matrices and Time-Reversal Symmetry for Measurements
slides: pdf
If a quantum state distributed over regions of space provides the expectation values of observables on those regions, what object provides the expectation values of observables measured sequentially in time? Such objects have recently been given a mathematically rigorous formulation and are called “states over time”. This formalism, together with the recent advances in categorical probability theory, has led to a notion of Bayes' rule in quantum theory. In this setting, Bayes' rule provides a method to calculate reverse processes that give rise to time-reversal symmetric expectation values of measurements. I will introduce these ideas, summarizing key concepts from references [1,2,3].
[1] Parzygnat, Fullwood “From time-reversal symmetry to quantum Bayes’ rules” PRX Quantum 4, 020334 (2023) arXiv:2212.08088
[2] Fullwood, Parzygnat “Operator representation of spatiotemporal quantum correlations” arXiv:2405.17555
[3] Parzygnat, Fullwood “Time-symmetric correlations for open quantum systems” arXiv:2407.11123
Dec 2024
-
09 Dec 2024
Search for Majorana Zero Modes in Full-Shell Hybrid Nanowires for Topological Quantum Computing
cf.: arXiv:1904.13374
Majorana fermions are fermions that were originally proposed in particle physics by Ettore Majorana and are characterized as being their own anti-particle. In condensed matter systems, Majorana quasiparticles occur as fractionalized excitations with an associated topologically protected degeneracy. In this talk, I will briefly review the basic concepts and recent developments in the study of Majorana zero modes in semiconductor-superconductor nanowires and -based superconductors, and discuss the possible quantum anomalous vortex and Majorana zero mode in full-shell hybrid nanowires.
Jan 2025
-
27 Jan 2025
Al-Amin Dhirani (University of Toronto, Canada):
Nanostructures: Building Blocks for Materials and Devices Exhibiting Tunable Quantum Behaviour
Many nanostructures can be fabricated with exquisite control over size, shape, and chemical composition. Such advances suggest an interesting opportunity: can we exploit this nanoscale control and fabricate bulk materials and devices with behaviour – potentially even quantum behaviour - that is tuned from the nanoscale up? In other words, can we “nanoengineer” quantum materials/devices? In this talk, I will describe examples showing that this is indeed possible. Using gold nanostructures and molecules as linkers, we have demonstrated materials that exhibit: an insulator-to-metal transition with varying linker molecule; the Kondo effect (delocalized – localize electrons hybridization) where the transition temperature that can be raised to above 220K by varying the nanostructure; and clear quantum particle-in-a-box, molecular wire transport where conductance increases with increasing molecule length (conductance of classical wires exhibit the opposite trend: conductance decreases with wire length). To further explore the potential role of hybridization at nanoscales, we developed a combined transistor – electrochemical cell device (“charge exchange transistor”) and found evidence that redox charge transfer in electrochemistry can occur through a 2-step mechanism involving a quantum transition state, proving a view of electrochemistry through a quantum lens. Our results highlight that nanostructured materials and devices are a promising platform for studying quantum phenomena with unprecedented control.
Feb 2025
-
3 Feb 2025
Wael Itani (Tandon School of Engineering, NYU):
Towards a Quantum Algorithm for Lattice Boltzmann (QALB) Simulation with a Nonlinear Collision Term
slides: pdf
cf. arXiv:2304.05915
The lattice Boltzmann method, a discrete velocity model for fluid dynamics, presents intriguing possibilities for quantum computation. This thesis develops three distinct approaches to quantum algorithms for lattice Boltzmann (QALB), each offering unique mathematical insights. First, we analyze the concurrent Carleman linearization of the collision and streaming, revealing how the nonlinear streaming operator maps to an infinite-dimensional linear system with exponentially suppressed truncation errors. Second, we construct the first completely unitary algorithm with a quantum linear embedding using bosonic operators and prove that the BGK collision operator’s symmetries enable its decomposition into Hermitian and constant non-Hermitian components. We show that embedding error is convergent for a general differential equation driven by a nonlinear polynomial. We demonstrate that while the quantum linear embedding achieves polylogarithmic scaling in spatial discretization, its gate complexity remains polynomial in Reynolds number. Finally, we explore quantum machine learning approaches to the collision operator, developing physics-informed quantum neural networks with embedded lattice Boltzmann symmetries. The quantum machine learning approach offers potential runtime advantages but requires significant improvements in training loss to handle physically relevant Reynolds numbers.
-
10 Feb 2025
Sam Bayliss (University of Glasgow):
Optically Addressable Spin Qubits in Chemically Synthesized Molecules
cf.: arXiv:2004.07998, arXiv:2402.07572
Optically addressable spins are a promising platform for quantum technologies due to their ability to be readily prepared, coherently controlled, and read out—exemplified by remarkable demonstrations with solid-state defects. Molecular materials are also attractive for hosting analogous optical-spin interfaces, with their chemical tunability and ability to be integrated with other systems offering promising functionality. Such properties could be beneficial for quantum sensing where, for example, precise spatial control between sensor and target is desired. To realise the potential of molecular spins for applications such as quantum sensing, the key combination of coherent spin manipulation and optical readout is desirable, combining sensitive detection capabilities with versatile control methods. In addition, such capabilities would ideally be accessible at room temperature. In this talk, I will describe examples of such functionality—ground-state molecular spins which can be optically interfaced, and excited-state spins which can realise high-contrast optically detected coherent control at room temperature—and outline how such systems are attractive as chemically synthesised spin qubits for quantum sensing.
-
17 Feb 2025
Francesco Ciccarello (University of Palermo):
Atom-photon bound states in modern quantum optics
slides: pdf
cf. arXiv:2402.10275, arXiv:2108.11963
Following recent technological advancements in experimental platforms such as circuit QED and ultracold atoms, the last decade has seen a growing interest in atom-photon bound states, which typically arise when a qubit is coupled to an engineered photonic lattice. Such states are key to a number of interesting effects such as fractional decay and, most of all, decoherence-free dipole-dipole interactions with potential applications for quantum information processing tasks. Here, we will present a (hopefully friendly) introduction to such states and the physics they give rise to. In the final part of the talk, we will show their generalization to the case of so called giant atoms. A giant atom is a new emergent paradigm of quantum optics; it is an artificial emitter that can couple to the field non-locally and as such can no longer be modelled as point-like system like in traditional quantum optics.
Apr 2025
-
7 Apr 2025
Simon Devitt (University of Technology Sydney)
Quantum communications networks are an important component in the quantum technology ecosystem. Currently in their infancy, quantum communication systems currently consist of point to point connections that are primary used for quantum key distribution protocols. Despite this infancy, there has been significant technological investment and progress, with several countries, most notably the Chinese, launching successful satellite systems demonstrating both Quantum Key Distribution and entanglement distribution over distances up to . Despite these achievements, the theoretical design and experimental construction of a quantum network that would mimic the distance and speed performance of the classical internet has been elusive. Specifically, the network performance of quantum repeater or quantum satellite systems, even under optimistic engineering assumptions, would be orders of magnitude worse than the classical internet, precluding the development of a quantum internet that would augment, or perhaps in the future, replace the current classical internet.
Our solution is a quantum variant of the sneakernet principle of network design. A downside of classical sneakernets is the issue of information latency. If the shipping route, for example, takes days, in not weeks, to transfer information from source to receiver then there is a significant latency between when the information is loaded onto a memory unit and when it is read out at the receiving end. In contrast, a quantum sneakernet does not suffer from significant latency on information transfer. Unlike a classical sneakernet, a quantum sneakernet does not transfer actual information. Instead, a quantum sneakernet distributes a quantum resource that can later be used for information teleportation protocols. Hence, this resource state is distributed slowly, offline, before any information is transmitted. We essentially prepare a virtual quantum “information pipeline” using sneakernet principles which can then be consumed at a later time to transmit quantum information.
In this work we describe large-scale quantum network architectures that are based on quantum sneakernet principles. We outline the basic information transfer protocols, what are the requirements of the quantum technology to realise this type of network and how a quantum sneakernet can be used to form a high-bandwidth, low error rate truck system to a quantum internet.
-
14 Apr 2025
Ramis Movassagh (Google):
Quantum supremacy and advantages beyond time-complexity
cf. nature:s41567-023-02131-2, arXiv:2501.18928
We will discuss various types of quantum advantages. We start with the state of the art complexity theoretical evidence for “quantum supremacy”. We then talk about a new result on secure delegation of quantum computation using random circuits, which we call “quantum function secret-sharing”.
-
21 Apr 2025
Yutaka Tabuchi (RIKEN Center for Quantum Computing)
Superconducting quantum computers in RIKEN
Superconducting quantum computers have garnered significant attention in recent years. Having their scalability and controllability, they are regarded as one of the most promising physical systems for realizing quantum computation. In this presentation, I will give an overview of the superconducting quantum computers based on the ones developed in RIKEN. Furthermore, I discuss gate schemes and control mechanisms for further improvements.
May 2025
-
05 May 2025
Malo Cadoret (ONERA, The French Aerospace Lab, Centre de Palaiseau):
Progress towards the development of a compact quantum cold-atom inertial measurement unit for onboard applications
Since the 1990’s, a new generation of inertial sensor based on matter-wave interferometry has appeared: accelerometers [1], gradiometers [2] and gyroscopes [3] have been developed and demonstrated high sensitivity, accuracy and long-term stability that outperforms the classical sensors. Major applications for atom interferometers are today geophysics, inertial navigation and fundamental physics. However, most of the quantum sensors are nowadays lab-based experiments and cannot perform onboard measurements, except for some notable exceptions such as ONERA’s marine and airborne gravimeter [4, 5]. In this talk, I will present our progress towards the development of a complete cold-atom Inertial Measurement Unit (IMU). Our goal is to have a single atomic sensor that will alternatively measure each inertial component (3 accelerations and 3 rotations). Every atomic measurement will be hybridized with a set of classical inertial sensors. Hybridization enables to combine the advantages of both classical and quantum technologies and to provide accurate continuous measurements with high dynamic range, in the scope of onboard inertial navigation compatibility. I will present our last results published in [6] regarding the development of a compact atomic gyroscope using magnetically-launched atoms.
[1] V. Menoret et al., Sci Rep 8, 12300 (2018).
[2] M. J. Snadden et al. Phys. Rev. Lett 81, 971 (1998)
[3] T.L. Gustavson et al., Phys. Rev. Lett 78 2046 (1997)
[4] Y. Bidel et al., Nat. Com. 9 627 (2018)
[5] Y. Bidel et al., J. Geod. 94 20 (2020)
[6] C. Salducci et al. Sci. Adv.10,eadq4498 (2024)
-
12 May 2025
Rishikesh Gajjala (NYUAD, CQTS):
Designing Quantum Experiments via Graph Theory
slides: pdf
Greenberger–Horne–Zeilinger (GHZ) states are quantum states involving at least three entangled particles. They are foundational in quantum information theory, with practical applications in quantum communication and cryptography. Krenn, Gu, and Zeilinger discovered a correspondence between a class of quantum‐optical experiments that produce GHZ states and edge‐weighted, edge‐coloured multigraphs called GHZ graphs. A graph parameter called dimension can be defined on such a graph, which equals the dimension of the GHZ state generated by the corresponding experiment. Constructing a GHZ graph with a large number of vertices and high dimension would be a major breakthrough, while proving the non‐existence of such graphs (and hence the experiments) has deep implications for quantum resource theory.
In this talk, I will present our results on this graph‐theoretic question and how they translate to quantum experiments. When there is no destructive interference, these experiments correspond to the special case of unweighted graphs. We provide a complete structural characterization of unweighted GHZ graphs for each dimension. In the more general (edge‐weighted) case, Cervera‑Lierta, Krenn, and Aspuru‑Guzik conjectured that the maximum dimension of an -vertex GHZ graph is less than . They verified this via SAT solvers for graphs with up to eight vertices, but nothing was known for larger values of n. We introduce a technique called local sparsification of GHZ graphs, with which we give the first analytical upper bound of on the dimension for simple GHZ graphs. Krenn and Gu made a stronger conjecture: that the dimension of any GHZ graph with more than four vertices is at most two (i.e., destructive interference does not help). We show that this holds for infinitely many graphs. Namely, graphs of vertex‐connectivity at most two and for all cubic graphs. Moreover, we prove that any minimal counterexample must be 4‑vertex‑connected. These structural insights both deepen our theoretical understanding and guide automated GHZ‐graph searches (e.g., via PyTheus).
Geometry, Topology & Physics (GTP) Seminar
Weekly seminar, broadly on topics in geometry, (algebraic) topology and theoretical/mathematical physics, with focus on applicability to high energy physics/string theory and quantum systems.
Feb 2022
-
02 Feb 2022
Luigi Alfonsi (University of Hertfordshire)
Higher quantum geometry and global string duality
video: rec
In this talk I will discuss the relation between higher geometric quantisation and the global geometry underlying string dualities. Higher geometric quantisation is a promising framework that makes quantisation of classical field theories achievable. This can be obtained by quantising either an ordinary prequantum bundle on the ∞-stack of solutions of the equations of motion or a categorified prequantum bundle on a generalised phase space. I will discuss how the higher quantum geometry of string theory underlies the global geometry of T-duality. In particular, I will illustrate how a globally well-defined moduli stack of tensor hierarchies can be constructed and why this is related to a higher gauge theory with the string 2-group. Finally, I will interpret the formalism of Extended Field Theory as an atlas description of the higher quantum geometry of string theory.
-
23 Feb 2022
Dmitri Pavlov (Texas Tech University)
The geometric cobordism hypothesis
video: rec
I will explain my recent work with Daniel Grady on locality of functorial field theories (arXiv:2011.01208) and the geometric cobordism hypothesis (arXiv:2111.01095). The latter generalizes the Baez–Dolan cobordism hypothesis to nontopological field theories, in which bordisms can be equipped with geometric structures, such as smooth maps to a fixed target manifold, Riemannian metrics, conformal structures, principal bundles with connection, or geometric string structures.
Applications include a generalization of the Galatius–Madsen–Tillmann–Weiss theorem, a solution to a conjecture of Stolz and Teichner on representability of concordance classes of functorial field theories, a construction of power operations on the level of field theories (extending the recent work of Barthel–Berwick-Evans–Stapleton), and a recent solution by Grady of a conjecture by Freed and Hopkins on deformation classes of reflection positive invertible field theories. If time permits, I will talk about the planned future work on nonperturbative quantization of functorial field theories and generalized Atiyah–Singer-style index theorems.
Mar 2022
-
08 March 2022
David White (Denison University, USA):
The Kervaire Invariant, multiplicative norms, and N-infinity operads
video: rec
In a 2016 Annals paper, Hill, Hopkins, and Ravenel solved the Kervaire Invariant One Problem using tools from equivariant stable homotopy theory. This problem goes back over 60 years, to the days of Milnorand the discovery of exotic smooth structures on spheres. Of particular importance it its solution were equivariant commutative ring spectra and their multiplicative norms. A more thorough investigation of multiplicative norms, using the language of operads, was recently conducted by Blumberg and Hill, though the existence in general of their new “N-infinity” operads was left as a conjecture. In this talk, I will provide an overview of the Kervaire problem and its solution, I will explain where the operads enter the story, and I will prove the Blumberg-Hill conjecture using a new model structure on the categoryof equivariant operads.
-
16 March 2022
Guo Chuan Thiang (Beijing University)
How open space index theory appears in physics
video: rec
The incredible stability of quantum Hall systems and topological phases indicates protection by an underlying index theorem. In contrast to Atiyah-Singer theory for compactified problems, what is required is an index theory on noncompact Riemannian manifolds, with interplay between discrete and continuous spectra. Input data comes not from a topological category a la TQFT, but a metrically-coarsened one. This is the subject of coarse geometry and index theory, and I will explain their experimental manifestations.
-
30 March 2022
Martin Palmer (Romanian Academy)
Mapping class group representations via Heisenberg, Schrödinger and Stone-von Neumann
video: Zoom
One of the first interesting representations of the braid groups is the Burau representation. It is the first of the family of Lawrence representations, defined topologically by viewing the braid group as the mapping class group of a punctured disc. Famously, the Burau representation is almost never faithful, but the Lawrence representation is always faithful: this is a celebrated theorem of Bigelow and Krammer and implies immediately that braid groups are linear (act faithfully on finite-dimensional vector spaces). Motivated by this, and by the open question of whether mapping class groups are linear, I will describe recent joint work with Christian Blanchet and Awais Shaukat in which we construct analogues of the Lawrence representations for mapping class groups of compact, orientable surfaces. Tools include twisted Borel-Moore homology of configuration spaces, Schrödinger representation of discrete Heisenberg groups and the Stone-von Neumann theorem.
Apr 2022
-
06 April 2022
Kiyonori Gomi (Tokyo Institute of Technology)
Differential KO-theory via gradations and mass terms
video: Zoom
Differential generalized cohomologies refine generalized cohomologies on manifolds so as to retain information on differential forms. The aim of my talk is to describe formulations of differential KO-theory based on gradations and mass terms. The formulation based on mass terms is motivated by a conjecture of Freed and Hopkins about a classification of invertible quantum field theories and by a model of the Anderson dual of cobordism theory given by Yamashita and Yonekura. I will start with an account of this background, and then describe the formulation of differential KO-theory. In the formulation a key role is played by a uperconnection associated to a mass term. This is a joint work with Mayuko Yamashita.
-
13 April 2022
Mario Velásquez (Universidad Nacional de Colombia)
The Baum-Connes conjecture for groups and groupoids
In this talk we present some basics definitions around the Baum-Connes conjecture in the context of groups and groupoids, in particular we define the reduced -algebra of a groupoid G. When a group (or groupoid) satisfies this conjecture we present how we can compute the topological K-theory of via a classifying space. We also present some explicit computations and an application about Fredholm boundary conditions in manifolds with corners.
-
27 April 2022
Amnon Neeman (Australian National University)
Bounded t-structures and stability conditions
We will give a gentle introduction to the topic. We will review the definitions of derived and triangulated categories, of t-structures an of stability conditions. The only new result will come at the very end of the talk, a theorem saying that there are no stability condition on the derived category of bounded complexes of vector bundles on a singular scheme.
May 2022
-
11 May 2022
Alex Fok (NYU Shanghai)
Equivariant twisted KK-theory of noncompact Lie groups
The Freed-Hopkins-Teleman theorem asserts a canonical link between the equivariant twisted K-theory of a compact Lie group equipped with the conjugation action by itself and the representation theory of its loop group. Motivated by this, we will present results on the equivariant twisted KK-theory of a noncompact semisimple Lie group . We will give a geometric description of generators of the equivariant twisted KK-theory of G with equivariant correspondences, which are applied to formulate the geometric quantization of quasi-Hamiltonian manifolds with proper G-actions. We will also show that the Baum-Connes assembly map for the -algebra of sections of the Dixmier-Douady bundle which realizes the twist is an isomorphism, and discuss a conjecture on representations of the loop group . This talk is based on joint work with Mathai Varghese.
Sep 2022
-
21 Sep 2022
Grigorios Giotopoulos (NYU Abi Dhabi)
Braided Homotopy Lie Algebras and Noncommutative Field Theories
cf.: arXiv:2112.00541
-
28 Sep 2022
David Jaz Myers (NYU Abu Dhabi, CQTS)
Objective Cohomology – Towards topological quantum computation
slides: pdf
In this talk, we will see the homotopy type theory point of view on defining pptwisted cohomology]] classes by means of bundle gerbes. We’ll take an increasingly less leisurely tour up the tower of cohomology degrees, seeing characters, principal bundles, central extensions, and characteristic classes along the way. Finally, we will go through the construction of the cohomology of the braid groups valued in the complex numbers, twisted by a complex character of the braid group. Through the work of many people, and in particular Feigin, Schechtman, Varchenko, the actions of the braid group of “defects” on the twisted complex cohomology of the braid group of “particles” is the monodromy action of the Knizhnik-Zamolodchikov connection on a space of conformal blocks. At CQTS we use this as a way to go from abstract homotopy type theory to protocols for topological quantum computation.
Oct 2022
-
05 Oct 2022
Adrian Clough (NYU Abu Dhabi, CQTS)
The smooth Oka principle
video: rec
notes: pdf
cf.: Clough 2021
The infinity topos of differentiable sheaves contains all smooth manifolds as a full subcategory and has excellent formal properties. In particular, it admits an intrinsic notion of underlying homotopy type of any differentiable sheaf, which coincides with classical constructions such as taking smooth total singular complexes. Moreover, there is a canonical sense in which the mapping sheaf between any two differentiable sheaves may have the correct homotopy type. This latter notion is reminiscent of the Oka principle in complex geometry. In this talk I will show how to exhibit the Oka principle in the smooth setting using model structures and other homotopical calculi on the infinity topos of differentiable sheaves.
-
12 Oct 2022
Salah Mehdi (U Lorraine and NYU Abu Dhabi)
Algebraic and geometric aspects of the Dirac equation
-
19 Oct 2022
Liang Kong (SIQSE and SUST)
Topological Wick Rotation and Holographic Dualities
video: rec
slides: pdf
on topological order, braided fusion categories and the holographic principle
-
26 Oct 2022
Urs Schreiber (NYU Abu Dhabi, CQTS)
Quantum Programming via Linear Homotopy Types
slides: see those for external talk at QTML2022
We first recall basic notions of quantum logic gates and quantum circuits, highlighting the conceptually more subtle issues of classical effects (measurements) and control (state preparation). Then we briefly review the formulation of computational effects and control via adjunctions and monads on data type type systems, in order to finally indicate basics of our observation that in any decent type system which has classically dependent linear data types, the relevant language structures for describing classical/quantum effects emerge naturally.
Nov 2022
-
09 Nov 2022
Zhen Huan (HUST)
Twisted Real quasi-elliptic cohomology
video: rec
Quasi-elliptic cohomology is closely related to Tate K-theory. It is constructed as an object both reflecting the geometric nature of elliptic curves and more practicable to study than most elliptic cohomology theories. It can be interpreted by orbifold loop spaces and expressed in terms of equivariant K-theories. We formulate the complete power operation of this theory. Applying that we prove the finite subgroups of the Tate curve can be classified by the Tate K-theory of symmetric groups modulo a certain transfer ideal. In this talk we construct twisted Real quasi-elliptic cohomology as the twisted KR-theory of loop groupoids. The theory systematically incorporates loop rotation and reflection. After establishing basic properties of the theory, we construct Real analogues of the string power operation of quasi-elliptic cohomology. We also explore the relation of the theory to the Tate curve. This is joint work with Matthew Young. [arXiv:2210.07511]
-
23 Nov 2022
Valentino Foit (NYUAD)
Brownian loops and conformally invariant systems
slides: pdf
The Brownian loop soup (BLS) is a stochastic system that is constructed from random loops in the plane and is invariant under conformal transformations. Correlation functions of certain observables can be used to formulate the BLS as a Conformal Field Theory (CFT). I will give an overview of CFTs in two dimensions and point out their relation to certain stochastic systems. Then I will discuss the BLS including some recent progress, such as the operator content, the continuous spectrum, and hints of an extended symmetry algebra.
-
30 Nov 2022
Classification and double commutant property for dual pairs in an orthosymplectic Lie supergroup
video: rec
One of the main problems in representation theory is to determine the set of equivalence classes of irreducible unitary representations of a Lie group. Using the Weil representation, Roger Howe established a one-to-one correspondence (known as the local theta correspondence) between particular representations of two subgroups and forming a dual pair in . This correspondence provides a nice way to construct unitary representations of small Gelfand-Kirillov dimension.
In his wonderful paper “Remarks on classical invariant theory”, Roger Howe suggested that his classical duality should be extendable to superalgebras/supergroups. In a recent work with Hadi Salmasian, we obtained a classification of irreducible reductive dual pairs in a real or complex orthosymplectic Lie supergroup . Moreover, we proved a “double commutant theorem” for all dual pairs in a real or complex orthosymplectic Lie supergroup.
In my talk, I will spend quite some time explaining how the Howe duality works in the symplectic case and then talk about the results we obtained in our paper with H. Salmasian. [arXiv:2208.09746]
Dec 2022
-
07 Dec 2022
Emily Riehl (Johns Hopkins University)
-Category theory for undergraduates
cf.: arXiv:2302.07855, AMS Notices
At its current state of the art, -category theory is challenging to explain even to specialists in closely related mathematical areas. Nevertheless, historical experience suggests that in, say, a century’s time, we will routinely teach this material to undergraduates. This talk describes one dream about how this might come about — under the assumption that 22nd century undergraduates have absorbed the background intuitions of homotopy type theory/univalent foundations.
-
14 Dec 2022
Eric Finster (University of Birmingham)
The -category of Types
slides: pdf
A major outstanding difficulty in Homotopy Type Theory is the description of coherent higher algebraic structures. As an example, we know that the algebraic structure possessed by the collection of types and functions between them is not a traditional 1-category, but rather an (∞,1)-category. In this talk, I will describe how the addition of a finite collection of additional definitional equalities designed to render the notion of “opetopic type” definable in fact allows one to construct the (∞,1)-category structure on the universe of types.
Jan 2023
-
25 Jan 2023
Thomas Creutzig (University of Alberta):
Representation Theory of affine vertex algebras
Recently there has been increased interest in non-semisimple braided tensor categories. Vertex algebras are a rich source of such categories and so I will give an overview on the representation theory of affine vertex algebras with a focus on the simplest example of . As we will see, already in this example quite rich and non-semisimple categories of modules appear.
-
01 Feb 2023
David Jaz Myers (CQTS @ NYU Abu Dhabi):
Simplicial, Differential, and Equivariant Homotopy Type Theory
cf.: arXiv:2301.13780
on cohesive homotopy type theory with two commuting notions of cohesion
Feb 2023
-
8 Feb 2023
Ruizhi Huang (Chinese Academy of Sciences)
Fractional structures on bundle gerbe modules and fractional classifying spaces
video: rec
cf.: arXiv:2203.14439
Both higher structures and bundle gerbe modules play important roles in modern geometry and mathematical physics. Bundle gerbe modules is a twisted version of vector bundles, and was introduced by Bouwknegt-Carey-Mathai-Murray-Stevenson in 2002. In particular, they introduced the twisted Chern character from the perspective of Chern-Weil theory. In a recent joint work with Han and Mathai, we study the homotopy theory aspects of the twisted Chern classes of torsion bundle gerbe modules. Using Sullivan’s rational homotopy theory, we realize the twisted Chern classes at the level of classifying spaces. The construction suggests a notion, which we call fractional U-structure serving as a universal framework to study the twisted Chern classes of torsion bundle gerbe modules from the perspective of classifying spaces. Based on this, we introduce and study higher fractional structures on torsion bundle gerbe modules parallel to the higher structures on ordinary vector bundles.
-
15 Feb 2023
Eugene Rabinovich (University of Notre Dame, USA)
Classical Bulk-Boundary Correspondences via Factorization Algebras
cf. arXiv:2202.12332 (a form of Poisson holography)
A factorization algebra is a cosheaf-like local-to-global object which is meant to model the structure present in the observables of classical and quantum field theories. In the Batalin-Vilkovisky (BV) formalism, one finds that a factorization algebra of classical observables possesses, in addition to its factorization-algebraic structure, a compatible Poisson bracket of cohomological degree +1. Given a “sufficiently nice” such factorization algebra on a manifold , one may associate to it a factorization algebra on .
The aim of the talk is to explain the sense in which the latter factorization algebra “knows all the classical data” of the former.
This is the bulk-boundary correspondence of the title. Time permitting, we will describe how such a correspondence appears in the deformation quantization of Poisson manifolds.
-
22 Feb 2023
Applied and Computational Topology
video: YT
We will give a brief introduction to the subject of Applied and Computational Topology. The survey of the subject’s main ideas and tools will be complemented with applications to discrete mathematics and to theoretical distributed computing. We will conclude with stating an open problem in combinatorial topology which is related to the complexity of the Weak Symmetry Breaking distributed task.
Mar 2023
-
1 Mar 2023
Deformation quantization and categorical factorization homology
video: YT
cf. arXiv:2107.12348
Moduli spaces of flat principal bundles on surfaces are a prominent object in mathematical physics, algebraic geometry and geometric representation theory. In particular they are the phase space of 3-dimensional Chern-Simons theory on a surface times an interval and hence equipped with a symplectic structure going back to the work of Atiyah and Bott. Various deformation quantizations of the algebra of functions have been constructed. Ben-Zvi, Brochier & Jordan constructed “local to global” quantizations using factorization homology of representation categories of quantum groups. Local to global constructions in this setting only work if the higher geometric structure of the moduli space of flat bundles is taken into account, i.e. it is treated as a moduli stack. In this setting the algebra of functions does not contain all the information and should be replaced by the category of quasicoherent sheaves.
In my talk we will explore categorifications of deformation quantization as deformations of symmetric monoidal categories (algebras over the -operad) into -categories and their interplay with factorization homology. The main result is that 2-dimensional factorization homology “commutes” with quantization in a way relating -quantizations to braided () quantizations. We will illustrate our results with examples from Poisson geometry and quantum groups. As a specific application we show that deformation quantizations of the moduli space of flat bundles based on Kontsevich integrals constructed by Li, Bland & Ševera are equivalent to quantizations constructed by Alekseev, Grosse & Schomerus based on quantum groups. The talk is based on joint work in progress with Eilind Karlsson, Corina Keller, and Jan Pulmann.
-
8 Mar 2023
Gereon Quick (Norwegian University of Science and Technology):
Geometric Hodge filtered complex cobordism
cf.: arXiv:2210.13259
video: YT
Differential cohomology theories on smooth manifolds play an important role in mathematical physics and other areas of mathematics. In their seminal work, Hopkins and Singer showed that every topological cohomology theory has a differential refinement. In this talk, I will first report on joint work with Mike Hopkins on a similar refinement of complex cobordism on complex manifolds which takes the Hodge filtration into account. I will then present joint work with Knut Haus in which we give a concrete geometric cycle model for this theory. This allows us to give a concrete description of an Abel-Jacobi type secondary invariant for topologically trivial cobordism cycles.
-
29 Mar 2023
João Faria Martins (Leeds University, UK)
Quinn Finite Total Homotopy TQFT as a once-extended TQFT
cf.: arXiv:2301.02491
video: YT
Quinn Finite Total Homotopy TQFT is a TQFT defined for any dimension, , of space, and that depends on the choice of a homotopy finite space, , (e.g. can be the classifying space of a finite group or of a finite 2-group). I will report on ongoing joint work with Tim Porter on once-extended versions of Quinn Finite total homotopy TQFT, taking values in the (symmetric monoidal) bicategory of groupoids, linear profunctors, and natural transformations between profunctors. The construction works in all dimensions, thus in particular it yields (0,1,2), (1,2,3) and (2,3,4)-extended TQFTs, any time we are given a homotopy finite space . I will show how to compute these once-extended TQFTs for the case when is the classifying space of a finite strict omega-groupoid, represented by a crossed complex.
Apr 2023
-
05 Apr 2023
Carmen Rovi (Loyola University, Chicago):
Relating cut and paste invariants and TQFTS
cf.: arXiv:1803.02939
video: YT
In this talk, we will be concerned with a relation between TQFTs and the cut-and-paste SKK invariants introduced by Karras, Kreck, Neumann, and Ossa. Cut-and-paste SKK invariants are functions on the set of smooth manifolds whose values on cut-and-paste equivalent manifolds differ by an error term depending only on the gluing diffeomorphisms. I will present a natural group homomorphism between the group of invertible TQFTs and the group of SKK invariants and describe how these groups fit into a split exact sequence. We conclude in particular that all positive real-valued SKK invariants can be realized as restrictions of invertible TQFTs.
-
12 Apr 2023
Matthias Ludewig (University of Regensburg, Germany)
The spinor bundle on loop space and its fusion product
cf.: arXiv:2206.09797
video: YT
We will discuss the definition of the spinor bundle on loop space and the construction of its fusion product, as suggested in a 2005 preprint by Stolz and Teichner. This is based on work by Kristel and Waldorf, involving some simplifications and additions due to myself.
-
Owen Gwilliam (University of Massachusetts, Amherst, USA)
A bulk-boundary correspondence with factorization algebras
cf.: arXiv:2001.07888
video: YT
Factorization algebras provide a flexible language for describing the observables of a perturbative quantum field theory, as shown in joint work with Kevin Costello. In joint work with Eugene Rabinovich and Brian Williams, we extended those constructions to a manifold with boundary for a special class of theories that includes, as an example, a perturbative version of the correspondence between chiral currents on a Riemann surface and abelian Chern-Simons theory on a bulk 3-manifold. (These methods extend to interacting theories, thanks to the thesis of Rabinovich.) Given time, I’ll sketch a systematic higher dimensional version for higher abelian CS theory on an oriented smooth manifold of dimension with boundary a complex manifold of complex dimension . The talk is expository, and it can be redirected according to the audience’s interests and requests.
-
26 Apr 2023
Jenny Wilson (University of Michigan, USA):
Stability patterns for braid groups and configuration spaces
cf.: arXiv:2201.04096
slides: pdf
video: YT
This talk will give an introduction of the field of ‘representation stability’. I will discuss how we can use representation theory to illuminate the structure of certain families of groups or topological spaces with actions of the symmetric groups, focusing on braid groups and configuration spaces as motivating examples.
May 2023
-
3 May 2023
Martina Rovelli (University of Massachusetts, Amherst, USA):
-Complicial sets as a model for -categories
cf.: arXiv:1809.10621, arXiv:2206.02689
video: YT
The formalism of extended TQFTs relies the notion of an -category: a categorical structure with morphisms in each dimension, which can be composed in a weakly associative way, and which are weakly invertible in dimension higher than . In this expository talk I will describe the notion of an -complicial set, explain the intuition for how this implements the idea of an -category, and discuss some of the advantages and disadvantages of this approach.
-
10 May 2023
David Ridout (University of Melbourne, Australia):
A (gentle) introduction to logarithmic conformal field theory
Conformal field theory is an integral part of modern mathematical physics with applications to statistical physics, string theory and pure mathematics. Textbooks teach us that such theories are built from chiral algebras (also called vertex operator algebras) with nice (semisimple) representation theories. But, what happens when the algebra has non-semisimple representations? This is the defining feature of logarithmic conformal field theory…
Sep 2023
-
13 Sep 2023
Mayuko Yamashita (Kyoto University, Japan):
Topological Modular Forms and Heterotic String Theory
cf. arXiv:2305.06196, arXiv:2108.13542
video: Zm
In this talk, I will explain my works with Y. Tachikawa to study anomalies in heterotic string theory via homotopy theory, especially the theory of Topological Modular Forms (TMF). TMF is an E-infinity ring spectrum which is conjectured by Stolz-Teichner to classify two-dimensional supersymmetric quantum field theories in physics. In the previous work [arXiv:2108.13542], we proved the vanishing of anomalies in heterotic string theory mathematically using TMF. Additionally, we have a recent update on the previous work [arXiv:2305.06196]. Due to the vanishing result, we can consider a secondary transformation of spectra, which coincides with the Anderson self-duality morphism of TMF. This allows us to detect subtle torsion phenomena in TMF by differential-geometric methods.
-
20 Sep 2023
Ulrich Pennig (Cardiff University):
Equivariant Higher Twisted K-Theory of via Exponential Functors
cf. arXiv:2307.00423
Twisted K-theory is a variant of topological K-theory that allows local coefficient systems called twists. For spaces and twists equipped with an action by a group, equivariant twisted K-theory provides an even finer invariant. Equivariant twists over Lie groups gained increasing importance in the subject due to a result by Freed, Hopkins and Teleman that relates the corresponding K-groups to the Verlinde ring of the associated loop group. From the point of view of homotopy theory only a small subgroup of all possible twists is considered in classical treatments of twisted K-theory. In this talk I will discuss an operator-algebraic model for equivariant higher (i.e. non-classical) twists over induced by exponential functors on the category of vector spaces and isomorphisms. These twists are represented by Fell bundles and the C*-algebraic picture allows a full computation of the associated K-groups at least in low dimensions. I will also draw some parallels of our results with the FHT theorem. This is joint work with D. Evans.
-
27 Sep 2023
Urs Schreiber (NYUAD, CQTS)
Quantum Channels as QuantumState Monad Transformations (Part II)
notes: here
video: Zm
The talk recalls some of the theory of “quantum channels” and then explains how this is captured by “monadic computation” with the linear version of the “State monad” – the “QuantumState Frobenius monad”.
Oct 2023
-
4 Oct 2023
Grigorios Giotopoulos (NYUAD)
Classical field theory in the topos of smooth sets
cf. Smooth Sets of Fields, arXiv:2312.16301
notes: pdf
By recalling the textbook description of a (variational) classical field theory and its critical locus of on-shell fields, I will list desiderata for a category in which this can rigorously take place. This category will consist of generalized smooth spaces, completely determined by “how they may be smoothly probed by finite dimensional manifolds”. By expanding on this intuition, I will describe how one naturally arrives at the definition of a smooth set as a “sheaf over the site of Cartesian spaces’’. I will then explain how the sheaf topos of smooth sets satisfies the desiderata of (variational) classical field theory. Time permitting, I will indicate how the setting naturally generalizes to include the description of fermionic fields, and (gauge) fields with internal symmetries.
-
11 Oct 2023
Cihan Okay (Bikent University):
Simplicial Distributions and Contextuality
cf. arXiv:2204.06648
In modern homotopy theory, spaces are represented by combinatorial models called simplicial sets. Their elegant formulation gives them great expressive power to capture spaces up to homotopy. Simplicial distributions are basic mathematical objects that mix simplicial sets with probabilities. That is, they model probability distributions on spaces. In my talk, I will show how simplicial distributions provide a framework for studying a central quantum feature associated with probabilities, known as contextuality. A typical measurement scenario consists of a set of measurements and outcomes, whereas simplicial distributions can be defined for spaces of measurements and outcomes. Our approach unifies and goes beyond two earlier approaches: the sheaf-theoretic (Abramsky-Brandenburger) and group cohomological (Okay-Roberts-Bartlett-Raussendorf).
-
18 Oct 2023
Chris Kapulkin (Western University, Canada):
Calculus of Fractions for Quasicategories (Part I)
cf.: arXiv:2306.02218
In their 1967 book “Calculus of Fractions and Homotopy Theory”, P. Gabriel and M. Zisman introduced calculus of fractions as a tool for understanding the localization of a category at a class of weak equivalences. While powerful, the condition of calculus of fractions is quite restrictive and it is rarely satisfied in various homotopical settings, like model categories or Brown‘s categories of fibrant objects, where one instead has homotopy calculus of fractions. This talk is based on a recent preprint arXiv:2306.02218, which aims to reconcile the two. We define calculus of fractions for quasicategories and give a workable model for marked quasicategories satisfying our condition. Although we have already found several applications of this result, we would be very interested in getting feedback from the audience and exploring new applications from diverse areas.
-
25 Oct 2023
Daniel Carranza (Western University, Canada):
Calculus of Fractions for Quasicategories (Part II)
cf.: arXiv:2306.02218
In their 1967 book “Calculus of Fractions and Homotopy Theory”, P. Gabriel and M. Zisman introduced calculus of fractions as a tool for understanding the localization of a category at a class of weak equivalences. While powerful, the condition of calculus of fractions is quite restrictive and it is rarely satisfied in various homotopical settings, like model categories or Brown‘s categories of fibrant objects, where one instead has homotopy calculus of fractions. This talk is based on a recent preprint arXiv:2306.02218, which aims to reconcile the two. We define calculus of fractions for quasicategories and give a workable model for marked quasicategories satisfying our condition. Although we have already found several applications of this result, we would be very interested in getting feedback from the audience and exploring new applications from diverse areas.
Nov 2023
-
01 Nov 2023
Juven Wang (Harvard University):
Ultra Unification, and Noninvertible Symmetry of the Standard Model from Gravitational Anomaly
cf.: arXiv:2012.15860, arXiv:arXiv:2302.14862
video: Zm
In the Standard Model, the total “sterile right-handed” neutrino number is not equal to the family number . The anomaly index had been advocated to play an important role in the previous work on Cobordism and Deformation Class of the Standard Model [arxiv:2112.14765, arxiv:2204.08393] and Ultra Unification [arXiv:2012.15860], in order to predict new highly entangled sectors beyond the Standard Model. Ultra Unification would combine the Standard Model and Grand Unification, particularly for the models with 15 Weyl fermions per family, without the necessity of right-handed sterile neutrinos, by adding new gapped topological phase sectors (in 4d or 5d) or new gapless interacting conformal sectors (in 4d) consistent with the nonperturbative global anomaly cancellation and cobordism constraints (especially from the mixed gauge-gravitational anomaly, such as a class anomaly, associated with the baryon minus lepton number B−L and the electroweak hypercharge ). Moreover, for the Standard Mode alone, the invertible B−L symmetry current conservation can be violated quantum mechanically by gravitational backgrounds such as gravitational instantons, hypothetically pertinent for leptogenesis in the very early universe. In specific, we show that a noninvertible categorical counterpart of the B−L symmetry still survives in gravitational backgrounds. In general, we construct noninvertible symmetry charge operators as topological defects derived from invertible anomalous symmetries that suffer from mixed gravitational anomalies. Examples include the perturbative local and nonperturbative global anomalies classified by and respectively. For this construction, we utilize the anomaly inflow concept, the 4d Pontryagin class and the gravitational Chern-Simons 3-form, the 3d Witten-Reshetikhin-Turaev-type topological quantum field theory with a framing anomaly corresponding to a 2d rational conformal field theory with an appropriate chiral central charge, and the 4d ^{TF}-time-reversal symmetric topological superconductor with 3d boundary topological order [arxiv:2302.14862].
-
08 Nov 2023
Theo Johnson-Freyd (Dalhousie University):
Higher Dagger Categories
slides: pdf
cf. categorified.net/dagger2023.html
Hilbert spaces form more than a category: their morphisms maps can be composed, but also every morphism has a distinguished “adjoint” , making it into a “dagger category”. This extra data is important for axiomatizing functional analysis, quantum mechanics, quantum information theory… However, the assignment is unsatisfying from a higher category theorist‘s perspective because it is “evil”, i.e. it violates the principle of equivalence: a category equivalent to a dagger category may not admit a dagger structure. This in particular interferes with generalizing the notion of dagger category to the (non-strict) higher categories necessary for axiomatizing fully-local quantum field theory. In this talk I will propose a manifestly non-evil definition of “dagger -category”. The same machinery also produce a non-evil definitions of “pivotal -category” and helps to clarify the relationship between reflection positivity and spin-statistics. This is based on joint work with B. Bartlett, G. Ferrar, B. Hungar, C. Krulewski, L. Müller, N. Nivedita, D. Penneys, D. Reutter, C. Scheimbauer, L. Stehouwer, and C. Vuppulury.
-
15 Nov 2023
Christoph Dorn (Oxford University):
Manifold Diagrams – A Brief Report
slides: pdf
cf.: arXiv:2208.13758
Manifold diagrams are the higher categorifications of string diagrams. They lie at the intersection of several interesting topics, such as: 1. The tangle and cobordism hypotheses, 2. The constructive description of free higher categorical structures, 3. The combinatorialization of differential structures and singularities. Nonetheless, the precise role of manifold diagrams in these topics remains largely mysterious. In this talk, we will focus on describing the basic interplay between (stratified) geometry, combinatorics, and (directed) cell complexes, exposed by the mathematical framework of manifold diagrams. This will include, in particular, two equivalent definitions of manifold diagrams, one geometric and one combinatorial, as well as a discussion of how these relate to the above topics
-
22 Nov 2023
Alberto Cattaneo (Zurich University, Switzerland):
Poisson Structures from Corners of Field Theories
slides: pdf
cf. arXiv:2310.01877
The BV formalism and its shifted versions in field theory have a nice compatibility with boundary structures. Namely, one such structure in the bulk induces a shifted (possibly degenerated) version on its boundary, which can be interpreted as a Poisson structure (up to homotopy). I will present the results for some field theories, in particular, 4D BF theory and 4D gravity.
Dec 2023
-
06 Dec 2023
Fiona Torzewska (University of Leeds, UK):
Topological Quantum Field Theories and Homotopy Cobordisms
slides: pdf
video: YT
cf: arXiv:2208.14504
I will begin by explaining the construction of a category , whose objects are topological spaces and whose morphisms are cofibrant cospans. Here the identity cospan is chosen to be of the form , in contrast with the usual identity in the bicategory of cospans over a category . The category has a subcategory in which all spaces are homotopically 1-finitely generated. There exist functors into from a number of categorical constructions which are potentially of use for modelling particle trajectories in topological phases of matter: embedded cobordism categories and motion groupoids for example. Thus, functors from into Vect give representations of the aforementioned categories. I will also construct a family of functors , one for each finite group , and show that topological quantum field theories previously constructed by Yetter, and an untwisted version of Dijkgraaf-Witten, generalise to functors from . I will construct this functor in such a way that it is clear the images are finite dimensional vector spaces, and the functor is explicitly calculable. I will also give example calculations throughout.
-
13 Dec 2023
Clover May (Norwegian University of Science and Technology):
Classifying Modules of Equivariant Eilenberg–MacLane Spectra
cf.: arXiv:2203.05287
Classically, since is a field, any module over the Eilenberg-MacLane spectrum splits as a wedge of suspensions of itself. Equivariantly, the module theory of -equivariant Eilenberg—MacLane spectra is much more complicated. For the cyclic group and the constant Mackey functor , there are infinitely many indecomposable -modules. Previous work together with Dugger and Hazel classified all indecomposable -modules for the group . The isomorphism classes of indecomposables fit into just three families. By contrast, we show for with an odd prime, the classification of indecomposable -modules is wild. This is joint work in progress with Grevstad.
Jan 2024
-
24 Jan 2024:
Central extensions of restricted Lie superalgebras and classification of -nilpotent Lie superalgebras in dimension 4
video: kt
cf.: arXiv:2401.08313
Over a field of positive characteristic , restricted Lie algebras are of prime interest, mainly due to their link to algebraic groups and their role in representation theory and classification. The cohomology associated with restricted Lie algebras is considerably more complicated than the ordinary Chevalley-Eilenberg cohomology and explicit formulas are only known up to order 2. In this talk, I will explain how to build the first and second restricted cohomology groups for restricted Lie superalgebras in characteristic greater than 3, modifying a previous construction. I will explain how these groups capture some algebraic structures, such as restricted extensions. Further, I will show how to apply this construction to classify -nilpotent restricted Lie superalgebras up to dimension 4 over an algebraically closed field of characteristic greater than 3. This is a joint work with Sofiane Bouarroudj (NYU Abu Dhabi).
-
31 Jan 2024
Geometry and Dualities of Decoupling Limits in String Theory and M-Theory
cf.: arXiv:2311.10564
Our understanding of M-theory is based on a duality web connecting different limits of the theory. I’ll discuss the extension of this duality web to a wide variety of decoupling limits related by duality to the null reduction of M-theory (and hence to the proposal that M-theory can be described by Matrix theory). From a modern perspective, these limits involve non-relativistic geometries, leading to new variants of supergravity in 11- and 10-dimensions. I’ll discuss how to systematically explore these corners of M-theory, following the roadmap of arxiv.org/abs/2311.10564.
Feb 2024
-
07 Feb 2024
Hank Chen (University of Waterloo, Canada):
Higher Anomaly Resolution from Algebras
This talk is based on arXiv:2211.08549, in which we explore the Lie higher-algebraic and higher-geometric structures that arise from a procedure we dub “gauging the gauge”, and study the resulting 2- and 3-gauge theory. The homotopy weakening of algebraic properties afforded by Lie -algebras is tied to violation of geometric higher-Bianchi conditions. In this talk, I will focus on the application of this observation to two specific cases, and examine its consequences. First, for the monopole gauge theory, the above observation gives rise to the 2-group Green-Schwarz anomaly cancellation (Benini-Cordova-Intriligator 2019), and the associated dipole conservation laws exhibit mobility restriction akin to fractonic matter (Slagel-Kim 2017). Second, for the string 2-gauge theory, we find a 3-group worth of charges exhibiting novel and intricate mobility restrictions and, under certain assumptions, the resulting 3-gauge theory achieves a higher-monopole charge which matched the fractional Pontrjagyn class . This gives a way in which the string structure of a spin manifold can be probed dynamically by a 3-group gauge theory.
-
14 Feb 2024
Babak Haghighat (Tsinghua University, China):
Flat Connections from Irregular Conformal Blocks
cf. arXiv:2311.13358, arXiv:2311.07960
I will talk about Liouville conformal blocks with degenerate primaries and one operator in an irregular representation of the Virasoro algebra. Using an algebraic approach, we derive modified BPZ equations satisfied by such blocks and subsequently construct corresponding integral representations based on integration over non-compact Lefschetz cycles. The integral representations are then used to derive novel types of flat connections on the irregular conformal block bundle.
-
28 Feb 2024
Joshua Lackman (Peking University, China):
A Groupoid Construction of Functional Integrals
video: kt
cf.: arXiv:2402.05866
We formalize Feynman’s construction of the path integral in the context of Lie algebroid-valued sigma models. To do this, we use the pair groupoid and the van Est map to define integration on manifolds in a coordinate-free way. We discuss applications to Brownian motion and the Poisson sigma model.
Mar 2024
-
06 Mar 2024
Du Pei (Centre for Quantum Mathematics, University of Southern Denmark):
On New Invariants and Phases of Supersymmetric Quantum Field Theories
In this talk, we will explore a novel approach to study supersymmetric quantum field theories using tools from stable homotopy theory. We will explain how this approach leads to new invariants that can be used to detect subtle differences between phases that escape the detection of more conventional invariants.
-
27 Mar 2024
Severin Bunk (University of Hertfordshire, UK):
Infinitesimal Higher Symmetries and Higher Connections
slides: pdf
Every bundle on a manifold has a universal symmetry group which controls all equivariant structures on the bundle. We modify this idea in two ways: we consider the infinitesimal version of universal symmetries and allow higher, or categorified bundles. These appear, for instance, in supergravity, and higher gauge theory, and more generally in geometry and topology. We will use a family-version of the Lurie-Pridham Theorem of derived deformation theory to construct these higher, infinitesimal analogues of universal symmetry groups. We then use this to provide a unified definition of connections on higher bundles and an algebraic formulation of differential cohomology. This extends work by Baez, Schreiber, Waldorf, Kapranov and others. Here, the curvature of a higher connection appears as an obstruction to infinitesimal equivariance. We elaborate in particular on the case of higher -bundles, or n-gerbes. This is joint work with Lukas Müller, Joost Nuiten and Richard Szabo.
Apr 2024
-
Alexander Stottmeister (Leibniz Universität Hannover):
Embezzlement of entanglement and the classification of von Neumann algebras
cf.: arXiv:2401.07299
We discuss the embezzlement of entanglement in the setting of von Neumann algebras and its relation to the classification of the latter. Embezzlement (of entanglement), introduced by van Dam and Hayden, denotes the task of producing any entangled state to arbitrary precision from a shared entangled resource state, the embezzling state, using local operations without communication while perturbing the resource arbitrarily little.
We show that Connes’ classification of type III von Neumann algebras can be given a quantitative operational interpretation in terms of embezzlement. This quantification implies that all type III factors, apart from some type factors, host embezzling states. In contrast, semifinite factors (type I or II) cannot host embezzling
May 2024
-
01 May 2024
Dmitry Melnikov (Federal University of Rio Grande do Norte, Brazil)
Chern-Simons States and Quantum Information
video: kt
cf. arXiv:2302.08548, arXiv:2312.16683
In this talk I will review the properties of quantum states in Chern-Simons theories from the perspective of topological quantum field theory paradigm. I will focus on the theory but the discussion can be generalized to other groups and other TQFTs. The discussion will single out a special class of “simple” states, whose properties are akin to the properties of classical geometry states in holography (AdS/CFT). Quantum entanglement and its properties will be discussed using the topological presentation, and I will give a few examples of the “topological engineering” of quantum resources and protocols. Time permitting I will also mention possible applications of the topological approach to the black hole information paradox.
-
08 May 2024
Explicit Quillen models for Cartesian products
slides: pdf
cf.: arXiv:2402.18168
Rational Homotopy Theory studies the homotopy type of ‘torsion-free’ topological spaces. This simplification has the advantage that we can associate an algebraic model to each space that contains all its rational information. This allows homotopy problems to be addressed computationally.
The use of differential graded Lie algebras to model spaces was developed by D. Quillen in the 60s of the last centuryowever, despite having algebraic models for each space, in some cases their effective calculation turns out to be very complex.
In this talk we will give explicit minimal Quillen models for the Cartesian products of certain spaces in terms of derivations of their models. The model presented also allows us to explicitly describe a model for the diagonal map. These explicit models are very useful to address the study of invariants such as the sectional category of a map which generalizes the the Lusternik-Schnirelmann category and Topological complexity.
-
13 May 2024
Iman Marivan (Duke University):
Locality, Symmetry, and Coherence Through the Lens of Quantum Information
The primary goal of quantum information science is to harness the power of quantum systems for computing and information-processing tasks. Interestingly, the quantum information perspective also provides new insights and raises new questions about the fundamental concepts of locality, symmetry, and coherence. In the first part of my talk, I will discuss an ongoing project focused on understanding the implications of symmetries and the locality of interactions within the framework of quantum circuits.
Sep 2024
-
04 Sep 2024
Alessandro Portaluri (University of Torino and NYUAD):
Index and Stability of (Semi-)Riemannian Closed Geodesics
cf. arXiv:1907.05864
A celebrated result proved by Poincaré affirms that a closed non-degenerate minimizing geodesic on an oriented surface is hyperbolic. Starting from this classical theorem and by using some recent results on the Maslov index and on the Spectral Flow, we will present a general instability criterion for timelike and spacelike closed (semi-)Riemannian geodesics on (non-)oriented manifolds of any dimension.
-
09 Sep 2024
Yassir Dinar (Sultan Qaboos University, Oman, and NYUAD):
Dubrovin-Frobenius Manifolds from Classical -Algebras
slides: pdf
cf.: arXiv:1911.00271
Dubrovin-Frobenius manifolds offer a remarkable geometric realization for potentials that satisfy the Witten-Dijkgraaf-Verlinde-Verlinde (WDVV) equations, which describe the moduli space of two-dimensional topological field theories. These manifolds have emerged in various branches of mathematics, including invariant theory, quantum cohomology, integrable systems, singularity theory, and information geometry.
A key method for constructing Dubrovin-Frobenius manifolds lies within the notion of local Poisson brackets of hydrodynamic type. Such a bracket can be obtained by considering the leading term of a local Poisson bracket admitting a dispersionless limit. On the other hand, we can construct, beginning from any nilpotent element in a simple Lie algebra, a local Poisson bracket known as classical -algebra using Drinfeld-Sokolov reduction.
In this talk, I will present recent findings and address the challenges involved in constructing Dubrovin-Frobenius manifolds from classical -algebras. I will also explore the geometric insights that arise from this process, offering new perspectives on the intricate relationship between algebraic structures and the geometric realization of Dubrovin-Frobenius manifolds.
-
18 Sep 2024
Mitchell Riley (CQTS @ NYUAD):
Lazy Algorithms in Algebraic Topology
Finite simplicial complexes are easily represented on a computer as lists of the simplices that they contain. In this form, it is not difficult to perform constructions involving them or compute invariants such as their homology. However, most spaces important to algebraic topology cannot be represented in this way, and so a new strategy is needed.
Effective Algebraic Topology is a collection of techniques for manipulating certain infinite simplicial sets algorithmically, retaining the ability to perform the same sorts of calculations as in the finite case. I will give an overview of the field and demonstrate some of the computations that can be performed.
Oct 2024
-
09 Oct 2024
Nikita Golub (Saint Petersburg State University):
Functorial Languages in Homological Algebra
slides: pdf
cf.: arXiv:2410.05708
In our talk, we shall dive into a number of phenomena related to the higher limit approach to the description of functors of homological nature. The first examples appeared in the work of Quillen on Hochschild homology of algebras, where he showed that Hochschild homology of an algebra can be represented as limits of some functors from the category of free extensions of a given algebra. Further similar formulas were derived by Roman Mikhailov and Sergey Ivanov in the context of group homology, who showed that group homology of a group can be expressed as higher limits of certain functors along the category of free extensions of the group. They further proposed the construction of fr-language, where and are some functorial ideals of the functor of group rings. It allows us to describe lots of graded functors from the category of groups to the category of abelian groups by simple expressions of the form , .
In our work, we have provided a formalisation of their construction and constructed new languages using the lower central series, which have a close connection with nilpotency. We notice that these functorial languages acquire remarkable properties when we restrict them to different varieties of groups.
We will lift all constructions to spectra and demonstrate that functorial languages on a given manifold of groups (or simply subcategories of a category of groups) give rise to some stable infinity-categories, which we call functorial surfaces. Then applying the algebraic K-theory to functorial surfaces, we arrive at flux spectra. This may provide a bridge between group theory and stable homotopy theory.
-
23 Oct 2024
Nizar Demni (Aix-Marseille Université (AMU) France and NYUAD):
From the Dunkl Intertwining Operator to Simple Hurwitz Numbers
slides: pdf
I’ll start with a review of finite root systems and their related matters (Weyl chambers, reflection groups, multiplicity functions). Then, I’ll introduce the Dunkl derivatives and the Dunkl intertwining operator. In this context, I’ll discuss the commutativity of the former and the existence of the latter, relying on a deformed de Rham cohomology and the reflection group algebra. Finally, I’ll focus on the Itzykson-Zuber-Harish-Chandra integral, its various expansions, and raise the problem of a mysterious connection to simple Hurwitz numbers.
Nov 2024
-
06 Nov 2024
Marco Benini (University of Genova, Italy):
A stacky approach to the comparison of axiomatizations of quantum field theory
slides: pdf
After a gentle introduction to Lorentzian quantum field theory as axiomatized by algebraic quantum field theory (Haag-Kastler, Brunetti-Fredenhagen-Verch, …) and by factorization algebras (Costello-Gwilliam, …), we shall present a categorical equivalence between these two axiomatic approaches that relies crucially on the intricate interplay between the principles of causality and determinism. We shall then rediscover this equivalence from a novel stacky perspective and illustrate why this point of view offers a promising solution to the open problem (motivated by gauge theory) of establishing a higher categorical analog of the above-mentioned equivalence, where the interplay between causality and determinism acquires a homotopical flavour.
-
20 Nov 2024
David Osten (University of Wroclaw, Poland):
Exceptional Generalised Geometry as a Symmetry Principle for Sigma Models
cf. 2402.10269
Exceptional field theory has been a useful technique in the investigation of supergravity. In this talk I will demonstrate that it can be applied to the world-volume point of view as well, as an alternative symmetry principle to supersymmetry. I present the construction of half-BPS brane sigma models in string and M-theory using only data from exceptional generalised geometry. When employing exceptional generalisd geometry these sigma models take a universal form in their Hamiltonian formulation which is expected to extend also to the enigmatic exotic branes. (Based on 2402.10269)
Dec 2024
-
04 Dec 2024
Lukas Woike (Bourgogne University, France):
Skein Algebras and Skein Modules Beyond Semisimplicity
slides: pdf
cf. arXiv:2409.17047, arXiv:2212.11259
Skein-theoretic methods play an important role for the construction of topological field theories and related structures. Classically, these methods use ribbon fusion categories as an input and hence need semisimplicity. In this talk, I will discuss generalizations of skein theory that work beyond semisimplicity, and partly even without rigid duals. To this end, I will give an overview of different joint papers with Brochier and Müller and explain the relation to work of Costantino-Geer-Patureau-Mirand, Brown-Haïoun and Runkel-Schweigert-Tham on admissible skeins.
-
11 Dec 2024
Simone Noja (Heidelberg University, Germany):
The Geometry of Pure Spinor Superfield Formalism
slides: pdf
cf.: arXiv:2404.07167
In this talk I will introduce a mathematical perspective on the pure spinor superfield formalism. In particular, I will discuss how multiplets of fields appearing in supersymmetric theories can be constructed mathematically from geometric data related to certain algebraic varieties – the nilpotence variety of the (super)symmetry algebra of the theory. After discussing some relevant examples, if time permits, I will hint at a generalization of the formalism in the direction of derived geometry.
Feb 2025
-
5 Feb 2025
Superinsulation: Magnetic Monopoles and Electric Confinement in Condensed Matter
slides: pdf
cf.: arXiv:1807.01984, arXiv:2008.12541, arXiv:2207.00791
Superinsulators are dual superconductors. They form as an emergent magnetic monopole condensate in which charges are bound by electric flux tubes (strings), realizing purely electric pions, and implying infinite electric resistance up to a finite critical temperature and critical voltage. Magnetic monopoles arise naturally in type-III superconductors with emergent granularity and they cause the Coulomb interaction to become even much stronger than in Mott insulators. I will review both the main aspects of the theory of superinsulation and the abundant experimental evidence supporting it, including an experiment directly measuring the linear Coulomb interaction due to electric strings. Finally, I will mention some possible technological applications of superinsulation, both as a standalone and in conjunction with superconductors.
-
12 Feb 2025
Shuhan Jiang (University of Zürich):
Cohomological Field Theories and Generalized Seiberg-Witten Equations
slides: pdf
cf. arXiv:2407.04019
We introduce a formalism for constructing cohomological field theories (CohFTs) from nonlinear partial differential equations. Applying this formalism to the generalized Seiberg-Witten equations offers a unified perspective on the full supersymmetric functionals of Donaldson-Witten, Seiberg-Witten, and Kapustin-Witten theories. We also outline a quantization program for this CohFT framework and discuss its potential to produce manifold invariants. This is joint work with Jürgen Jost.
-
19 Feb 2025
Federico Bonetti (University of Murcia, Spain):
Generalized global symmetries from string theory
slides: pdf
cf.: arXiv:2412.07842, arXiv:2306.16405
Global symmetries are extremely useful in the study of quantum field theories (QFTs). Remarkably, the notion of global symmetry in QFT has undergone a dramatic generalization in recent years, based on the idea that symmetries correspond to topological operators. In this talk, I will discuss aspects of generalized symmetries of QFTs realized in string/M-theory. The stringy perspective complements the purely field-theoretical point of view and allows us to study non-trivial classes of strongly coupled QFTs. By means of concrete examples, I will illustrate how generalized symmetry structures can be extracted systematically from the topology and geometry of the string background that realizes the QFT.
Mar 2025
-
5 Mar 2025
Leonardo Santilli (Tsinghua University, China):
Defects, SymTFTs, and -form symmetry from M-theory
slides: pdf
cf.: arXiv:2411.19683
I will highlight some tensions in the treatment of higher form symmetries, when the theory possesses a -form symmetry. I will then show how, for invertible symmetries, the tensions are automatically resolved dealing with -form symmetries in the formalism of gerbes. After this general introduction and motivation, I will review the geometric engineering of defects in M-theory. I will then proceed to obtain the SymTFT of M-theory compactifications, using differential cohomology as the main tool. In this way, I will provide a comprehensive treatment of defects and symmetries via geometric engineering, and derive the -form symmetries and their anomalies from this perspective. I will conclude with explicit examples and dynamical applications.
-
26 Mar 2025
Tim Hosgood (Topos Institute, Oxford, UK):
Čech data for holomorphic Chern classes
cf.: arXiv:2003.10023
Given a complex manifold and a coherent analytic sheaf, it is of interest to construct the corresponding Chern classes in some cohomology theory. In (truncated) de Rham cohomology, things can be done explicitly: one can write down Čech representatives in terms of the transition functions of the (simplicial) vector bundles in a resolution of the coherent sheaf. In Deligne cohomology there is an abstract proof of existence, but (as far as the speaker is aware) no equally explicit construction is known. In this talk, I will explain the construction of the Čech data in de Rham cohomology, and why it doesn’t transfer over to Deligne cohomology.
Apr 2025
-
17 Apr 2025
Gil Cavalcanti (Utrecht University, The Netherlands):
T-duality from circles to spheres and beyond
slides: pdf
cf. arXiv:2503.20143, arXiv:2405.14054
I will introduce the definition and basic properties of usual abelian T-duality and present extensions to sphere bundles and more general fibrations.
-
23 Apr 2025
Alberto Ibort (Universidad Carlos III of Madrid, Spain)
The groupoid picture of Quantum Mechanics
slides: pdf
video: zm
cf. arXiv:2002.09326
The groupoid picture of Quantum Mechanics is the formal expression of Schwinger’s conceptualisation of quantum mechanics, that drinks directly from the original ideas by Bohr and Heisenberg on the fundamental role played by physical transitions in the description of quantum phenomena. In this talk we will review some of the fundamental notions leading to this picture and will discuss some applications regarding the dynamical description of quantum theories.
-
30 Apr 2025
Rongvoram Nivesvivat (NYUAD):
Three-point connectivities of interfaces in 2D critical statistical models.
slides: pdf
cf.: arXiv:2311.17558, arXiv:2302.08168
It is widely conjectured that the critical limit of interfaces of statistical models, such as hull percolations and the Ising domain walls, can be described by conformally-invariant quantum field theory, known as conformal field theory (CFT). Using the technology from CFT, we will propose the closed expression for a large class of three-point connectivities of interfaces in 2D critical statistical models. Our conjectures have been tested to be in an excellent agreement with the transfer matrix formalism based on the Temperley-Lieb algebra. Moreover, the special case of our result that describes the probability of having 3 points on the same hull percolation perfectly coincides with the same result from the conformal loop ensembles by Xin Sun al. Up to our best knowledge, this is one of the first instances where we have a non-trivial agreement between CFT and conformal loop ensembles.
May 2025
-
07 May 2025
Matthew Yu (Oxford University, UK)
A new tangential structure for type IIA string theory
slides: pdf
cf.: arXiv:2411.07299
The Green-Schwarz anomaly cancellation condition says that the target space of heterotic string theory must come with a string structure for the theory to be consistent. In this talk we discuss a new tangential structure called , first introduced by Devalapurkar, as a analogue of string. Approximating the correct tangential structure of string theory has many implications, primarily is the Swampland program via the cobordism conjecture of Mcnamara and Vafa. We will show that the spectrum of has the notable property that it orients , just like how the spectrum of string orients tmf, by the work of Ando-Hopkins-Rezk. Finally we will show that the anomaly condition of the partition function of M-theory, studied by Diaconescu-Moore-Witten is implied by a structure on the target space of type IIA, in parallel to the Green-Schwarz anomaly for heterotic string theory, and discuss applications for anomaly cancellation.
External presentations
The following is a (very) inclomplete list of selected invited presentations by CQTS members at other institutes.
Sep 2022
-
15 Sep 2022 at PlanQC 2022
Urs Schreiber on joint work with Hisham Sati:
Topological Quantum Programming in TED-K
slides: pdf (view full screen)
video: YT
extended abstract: arXiv:2209.08331
-
16 Sep 2022 at Math Faculty Meeting, NYU Abu Dhabi
Urs Schreiber on joint work with Hisham Sati:
Practical Foundations for Topological Quantum Programming
slides: pdf
Nov 2022
-
12 Nov 2022 at Workshop on Quantum Software, satellite of QTML 2022 (Naples, Italy)
Urs Schreiber on joint work with D. J. Myers, M. Riley and H. Sati:
Quantum Data Types via Linear Homotopy Type Theory
slides: pdf
The proper concept of data types in quantum programming languages, hence of their formal verification and categorical semantics, has remained somewhat elusive, as witnessed by the issue of “dynamic lifting” encountered in the Quipper language family. In this talk I explain our claim that a powerful quantum data type-system elegantly solving these problems is naturally provided by the linear homotopy type theory recently realized by M. Riley. Together with our previous claim that homotopy type theory natively knows about the fine detail of (2)-anyon braid quantum gates, this shows that linear homotopy type theory is a natural substrate for typed quantum programming languages aware of topological quantum hardware.
Dec 2022
-
17 Dec 2022 at AQIS 2022
Braidless Topological Quantum Teleportation
poster: pdf
on quantum teleportation with/of anyons
Jan 2023
-
15 Jan 2023
M-theory and matter via Twisted Equivariant Differential (TED) K-theory
talk at M-Theory and Mathematics 2023, NYU Abu Dhabi
[links]
-
15 Jan 2023
Topological Quantum Gates from M-Theory
talk at M-Theory and Mathematics 2023, NYU Abu Dhabi
[links]
Feb 2023

-
20 Feb 2023
Simulating an all-optical quantum controlled-NOT gate using soliton scattering by a reflectionless potential well
talk at UAE U Nonlinear Physics Group Conference, Al Ain
Mar 2023

Asif Equbal (far left) and Amaria Javed (far right)
Apr 2023
-
10 Apr 2023
How do you identify one thing with another? – an intro to Homotopy Type Theory
talk at Prof. Sadok Kallel‘s colloquium,
American University of Sharjah
slides: pdf
-
Effective Quantum Certification via Linear Homotopy Types — Part I
talk at Colloquium of the Topos Institute
slides: pdf (view full screen)
video: YT
Aug 2023
-
Effective Quantum Certification via Linear Homotopy Types — Part II
talk at Colloquium of the Topos Institute
slides: pdf (view full screen)
video: YT
Feb 2024
-
02 Feb 2024
Topological Quantum Programming with Linear Homotopy Types
talk at: Homotopy Type Theory Electronic Seminar,,
video: YT
-
28-29 Feb 2024
Asif Equbal and Amaria Javed presenting the CQTS booth at:

-
29 Feb 2024
speaking at the Gala dinner of

Jul 2024
Sep 2024
-
18 Sep 2024
Grigorios Giotopoulos (NYU AD):
Sheaf Topos Theory as a setting for Physics
talk at Workshop on Noncommutative and Generalized Geometry in String Theory, Corfu Summer Institute
slides: [pdf]
on (quantum) field theory expressed in the topoi of smooth sets and super smooth sets.
-
Sep 2024
CNN’s “Decoding Quantum Computation”
briefly mentions (in minute 20:00)
Feb 2025
-
21 Feb 2025
Homotopy Theory for Topological Quantum Computing
talk at: 4th Int. Conference on Math and Statistics (ICMS 2025), American University of Sharjah
-
24-28 Feb 2025
Quantum Language via Linear Homotopy Types
mini-course at IX International Workshop on Information Geometry, Quantum Mechanics and Applications 2025, ICMAT Madrid,
Jul 2025
Feature at Quantum Zeitgeist:
Last revised on August 27, 2025 at 18:14:27. See the history of this page for a list of all contributions to it.

