nLab linear chord diagram
Note: linear chord diagram and linear chord diagram both redirect for "rooted chord diagram".
Context
Graph theory
Properties
Extra properties
Extra structure
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
A linear chord diagram or arc diagram or rooted chord diagram is a trivalent finite undirected graph with an embedded oriented line and all vertices on that line.
Equivalemtly this is just an n-tuple equipped with a partition into pairs.
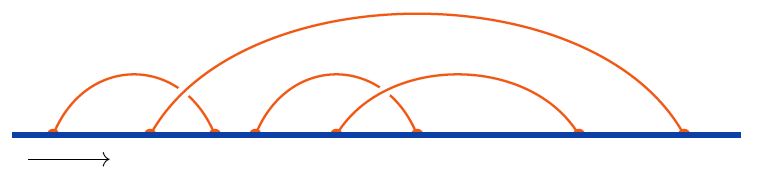
The following shows a generic example of a linear chord diagram:
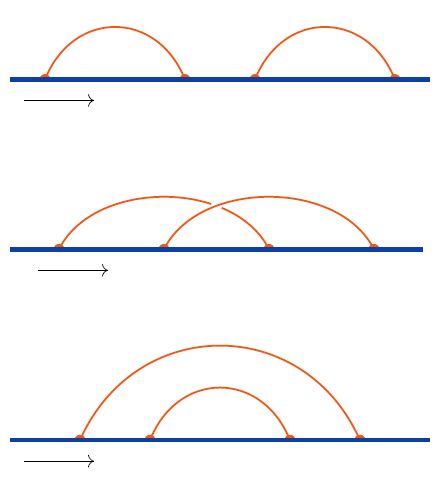
The graphics on the right shows all linear chord diagrams with precisely four vertices.
Closing up the line of a linear chord diagram to a circle and remembering the ordering of vertices only op to cyclic permutation, it becomes a round chord diagram, usually just called a chord diagram. Conversely, a linear chord diagram is equivalently a round chord diagram with one of its vertices singled out.
graphics from Sati-Schreiber 19c
Applications
Wick’s theorem
The combinatorics of contractions in Wick's theorem is governed by linear chord diagrams:
Let be a set of quantum fields/random variables which are free fields/multivariate normally distributed with
Then Wick's theorem says that the expectation value of the product of of these fields/random variables is the sum over linear chord diagrams with vertices of the product over the edges of the given chord diagram of the factors .
For example, for , Wick's theorem says this:
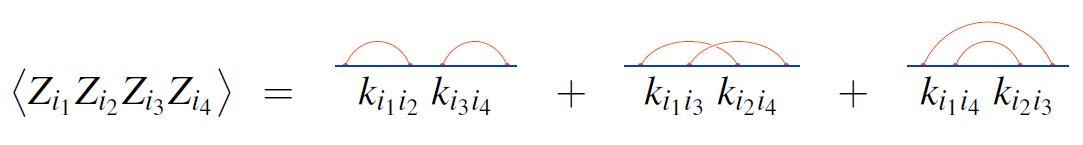
Related concepts
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
References
- Everett Sullivan, Linear chord diagrams with long chords (arXiv:1611.02771)
Last revised on January 10, 2020 at 08:26:23. See the history of this page for a list of all contributions to it.