nLab D-brane

Contents

Context

String theory

Idea

An abstractly defined $n$ -dimensional quantum field theory is a consistent assignment of state-space and correlators to $n$ -dimensional cobordisms with certain structure (topological structure, conformal structure, Riemannian structure, etc. see FQFT/AQFT). In an open-closed QFT the cobordisms are allowed to have boundaries.

In this abstract formulation of QFT a D-brane is a type of data assigned by the QFT to boundaries of cobordisms.

For a broader perspective see at brane.

In $2d$ rational CFT

A well understood class of examples is this one: among all 2-dimensional conformal field theory that case of full rational 2d CFT has been understood completely, using FFRS-formalism. It is then a theorem that full 2-rational CFTs are classified by

a modular tensor category $\mathcal{C}$ (to be thought of as being the category of representations of the vertex operator algebra of the 2d CFT);
a special symmetric Frobenius algebra object $A$ internal to $\mathcal{C}$ .

In this formulation a type of brane of the theory is precisely an $A$ -module in $\mathcal{C}$ (an $A$ -bimodule is a bi-brane or defect line ):

the 2d cobordisms with boundary on which the theory defined by $A \in \mathcal{C}$ carry as extra structure on their connected boundary pieces a label given by an equivalence class of an $A$ -module in $\mathcal{C}$ . The assignment of the CFT to such a cobordism with boundary is obtained by

triangulating the cobordism,
labeling all internal edges by $A$
labelling all boundary pieces by the $A$ -module
all vertices where three internal edges meet by the multiplication operation
and all points where an internal edge hits a boundary by the corresponding action morphism
and finally evaluating the resulting string diagram in $\mathcal{C}$ .

So in this abstract algebraic formulation of QFT on the worldvolume, a brane is just the datum assigned by the QFT to the boundary of a cobordism. But abstractly defined QFTs may arise from quantization of sigma models. This gives these boundary data a geometric interpretation in some space. This we discuss in the next section.

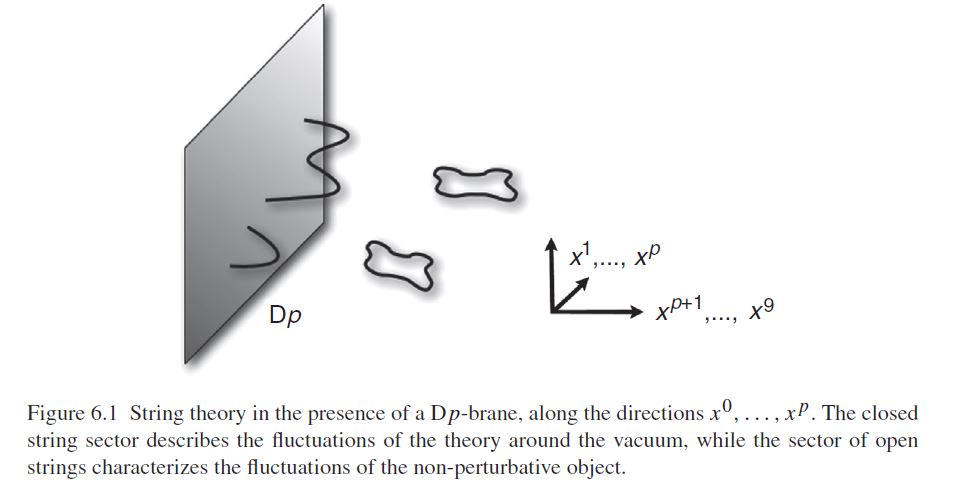
graphics grabbed from Ibanez-Uranga 12

In $2d$ TFT

Another case where the branes of a QFT are under good mathematical control is TCFT: the (infinity,1)-category-version of a 2d TQFT.

Particularly the A-model and the B-model are well understood.

the branes of the B-model (“B-branes”) form the the stable (infinity,1)-category of chain complexes of quasicoherent sheaves on the target space (often considered just in terms of its homotopy category of an (infinity,1)-category, the derived category of quasicoherent sheaves);
the branes of the A-model form the Fukaya category of the target space.
the category of D-branes of the A-model on a symplectic Landau-Ginzburg model, is a Fukaya-Seidel category;
the category of D-branes of the B-model on a complex Landau-Ginzburg model is a category of matrix factorizations.

There is also a mathematical structure called string topology with D-branes. At present this is more “string inspired” than actually derived from string theory, though.

In terms of geometric data of the $\sigma$ -model background

An abstractly defined QFT (as a consistent assignment of state spaces and propagators to cobordisms as in FQFT) may be obtained by quantization from geometric data :

Such a sigma-model QFT is the quantization of an action functional on a space of maps $\Sigma \to X$ from a cobordism (“worldvolume”) $\Sigma$ to some target space $X$ that may carry further geometric data such as a Riemannian metric, or other background gauge fields.

One may therefore try to match the geometric data on $X$ that encodes the $\sigma$ -model with the algebraic data of the FQFT that results after quantization. This gives a geometric interpretation to many of the otherwise purely abstract algebraic properties of the worldvolume QFT.

It turns out that if one checks which geometric data corresponds to the $A$ -modules in the above discussion, one finds that these tend to come from structures that look at least roughly like submanifolds of the target space $X$ . And typically these submanifolds themselves carry their own background gauge field data.

A well-understood case is the Wess-Zumino-Witten model: for this the target space $X$ is a simple Lie group $X = G$ and the background field is a circle 2-bundle with connection (a bundle gerbe) on $G$ , representing the background field that is known as the Kalb-Ramond field.

In this case it turns out that branes for the sigma model on $X$ are given in the simplest case by conjugacy classes $D \subset G$ inside the group, and that these carry twisted vector bundle with the twist given by the Kalb-Ramond background bundle. These vector bundles are known in the string theory literature as Chan-Paton vector bundles . The geometric intuition is that a QFT with certain boundary condition comes from a quantization of spaces of maps $\Sigma \to G$ that are restricted to take the boundary of $\Sigma$ to these submanifolds.

More generally, one finds that the geometric data that corresponds to the branes in the algebraically defined 2d QFT is given by cocycles in the twisted differential K-theory of $G$ . These may be quite far from having a direct interpretation as submanifolds of $G$ .

The case of rational 2d CFT considered so far is only the best understood of a long sequence of other examples. Here the collection of all D-branes – identified with the collection of all internal modules over an internal frobenius algebra, forms an ordinary category.

More generally, at least for 2-dimensional TQFTs analogous considerations yield not just categories but stable (∞,1)-categories of boundary condition objects. For instance, for what is called the B-model 2-d TQFT the category of D-branes is the derived category of coherent sheaves on some Calabi-Yau space.

Starting with Kontsevich’s homological algebra reformulation of mirror symmetry the study of (derived) D-brane categories has become a field in its own right in pure mathematics.

… lots of further things to say …

As black branes

In perturbative string theory, hence for small string coupling constant the D-branes are incarnated as boundary conditions for the string’s worldsheet 2d CFT, exhibiting submanifolds in spacetime. As the string coupling constant increases and becomes non-perturbative, this picture of perturbative string theory breaks down, but at low energy (large scales) now supergravity becomes a good description, and now the D-branes are incarnated as black branes.

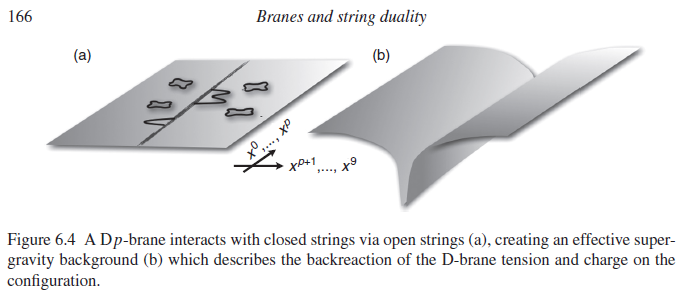
graphics grabbed from Ibanez-Uranga 12

This transition is also the key to understanding black holes in string theory.

1/2 BPS black branes in supergravity: D-branes, F1-brane, NS5-brane, M2-brane, M5-brane

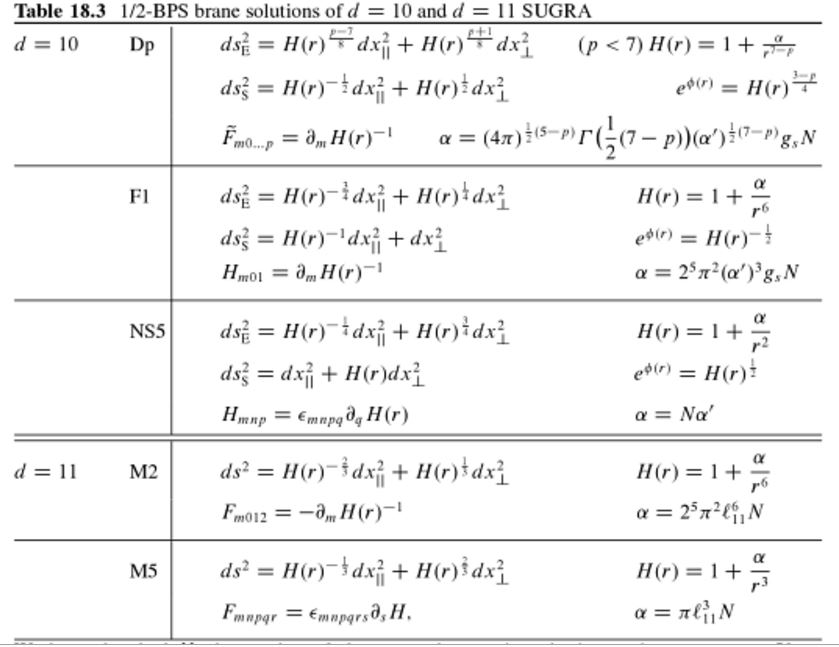
(table from Blumenhagen, Lüst & Theisen 2013, Chapter 18.5)

Examples

Various dimensions

In type IIA supergravity

D0-brane, D2-brane, D4-brane, D6-brane, D8-brane.

In type IIB supergravity

D1-brane, D3-brane, D5-brane, D7-brane

In the WZW model

For D-branes in the WZW-model see WZW-model – D-branes.

Properties

As F-branes originating from M-branes

from M-branes to F-branes: superstrings, D-branes and NS5-branes

M-theory on $S^1_A \times S^1_B$ -elliptic fibration	KK-compactification on $S^1_A$	type IIA string theory	T-dual KK-compactification on $S^1_B$	type IIB string theory	geometrize the axio-dilaton	F-theory on elliptically fibered-K3 fibration	duality between F-theory and heterotic string theory	heterotic string theory on elliptic fibration
M2-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	type IIA superstring	$\mapsto$	type IIB superstring	$\mapsto$	“	$\mapsto$	heterotic superstring
M2-brane wrapping $S_B^1$	$\mapsto$	D2-brane	$\mapsto$	D1-brane	$\mapsto$	“
M2-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ strings and $q$ D2-branes	$\mapsto$	(p,q)-string	$\mapsto$	“
M5-brane wrapping $S_A^1$	double dimensional reduction $\mapsto$	D4-brane	$\mapsto$	D5-brane	$\mapsto$	“
M5-brane wrapping $S_B^1$	$\mapsto$	NS5-brane	$\mapsto$	NS5-brane	$\mapsto$	“	$\mapsto$	NS5-brane
M5-brane wrapping $p$ times around $S_A^1$ and $q$ times around $S_B^1$	$\mapsto$	$p$ D4-brane and $q$ NS5-branes	$\mapsto$	(p,q)5-brane	$\mapsto$	“
M5-brane wrapping $S_A^1 \times S_B^1$	$\mapsto$		$\mapsto$	D3-brane	$\mapsto$	“
KK-monopole/A-type ADE singularity (degeneration locus of $S^1_A$ -circle fibration, Sen limit of $S^1_A \times S^1_B$ elliptic fibration)	$\mapsto$	D6-brane	$\mapsto$	D7-branes	$\mapsto$	A-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 2)		SU-gauge enhancement
KK-monopole orientifold/D-type ADE singularity	$\mapsto$	D6-brane with O6-planes	$\mapsto$	D7-branes with O7-planes	$\mapsto$	D-type nodal curve cycle degeneration locus of elliptic fibration (Sen 97, section 3)		SO-gauge enhancement
exceptional ADE-singularity	$\mapsto$		$\mapsto$		$\mapsto$	exceptional ADE-singularity of elliptic fibration	$\mapsto$	E6-, E7-, E8-gauge enhancement

(e.g. Johnson 97, Blumenhagen 10)

Characterization in terms of Dirac structures

D-branes may be identified with Dirac structures on a Courant Lie 2-algebroid over spacetime related to the type II geometry (Asakawa-Sasa-Watamura). See at Dirac structure for more on this.

D-brane charge

In analogy to how in electromagnetism magnetic charge is given by a class in ordinary cohomology, so D-brane charge is given in (twisted) K-theory, or, if preferred, in its image under the Chern character.

The Chan-Paton bundle carried by a D-brane defines a class in twisted K-theory on the D-brane worldvolume and the D-brane charge is the push-forward (Umkehr map) of this class to spacetime, using a K-orientation of the embedding of the D-brane (a spin^c structure).

See at K-theory classification of D-brane charge

General

More in detail this means the following (BMRS2).

Let $X$ be a manifold regarded as spacetime and $i \colon Q \hookrightarrow X$ a submanifold regarded as the worldvolume of a D-brane. For $\nabla_B \colon X \to \mathbf{B}^2 U(1)_{conn}$ the circle 2-bundle with connection which models the background B-field, write $\chi_B \colon X \to \mathbf{B}^2 U(1)$ for the underlying circle 2-group-principal 2-bundle.

The corresponding Chan-Paton bundle (a twisted line bundle for the case of a single D-brane) is the trivialization $\xi$ in

\array{ && Q \\ & \swarrow && \searrow^{\mathrlap{i}} \\ \ast && \swArrow_{\xi} && X \\ & \searrow && \swarrow_{\mathrlap{\chi_B}} \\ && \mathbf{B}^2 U(1) } \;\;\;\;\; \simeq \;\;\;\;\; \array{ && Q \\ & \swarrow &\downarrow& \searrow^{\mathrlap{i}} \\ \ast &\swArrow_{\xi}& \downarrow^{\mathrlap{i^\ast \chi_B}} &\swArrow_{id}& X \\ & \searrow &\downarrow& \swarrow_{\mathrlap{\chi_B}} \\ && \mathbf{B}^2 U(1) } \,.

Assuming that $i \colon Q \to X$ is K-oriented in that for instance $X$ has a spin-structure and $Q$ a spin^c-structure, then under the groupoid convolution algebra functor $C^\ast$ this is incarnated as a Hilbert bimodule which defines a class in twisted operator K-theory, realized as the following comoposite in KK-theory

\mathbb{C} \stackrel{\Gamma(\xi)}{\to} C(Q)_{i^\ast \chi_B} \stackrel{i_!}{\to} C(X)_{\chi_B} \,,

where

$C(Q)$ and $C(X)$ are the C*-algebras of functions (vanishing at infinity) on the D-brane and on spacetime, respectively;
$C(X)_{\chi_B}$ is the groupoid convolution algebra of sections of $\chi_B$ regarded as a centrally extended groupoid over a Cech groupoid resolution of $X$ which supports a Cech cocycle for $\chi_B$ , and similarly for $C(Q)_{i^\ast \chi B}$ and the pullback/restriction $i^\ast \chi_B$ of the background B-field to the brane;
$i!$ is the push-forward (Umkehr map) dual to $i^\ast \colon C(X)_{\chi_B} \to C(Q)_{i^\ast \chi_B}$ , realizes as a KK-theory class

$D_Q = i! = \in KK(C(Q), C(X)_{\chi_B}) \,.$

The corresponding D-brane charge in KK-theory is the resulting composite (relative index)

i_!(\xi) = D_Q(\xi) \in KK(\mathbb{C}, C(X)_{\chi_B}) \simeq K^{[\chi_b]}(X)

in twisted K-theory. Traditionally only the image of this under the Chern character

ch \colon KK \to HL

in real cohomology/cyclic cohomology is considered, $ch(D_Q(\xi))$ . Moreover, traditonally one thinks of first applying $ch$ to $\xi$ and then pushing forward in $HL$ . By the C*-algebraic Grothendieck-Riemann-Roch theorem this gives the isomorphic expression

ch(D_Q(\xi)) \otimes_{C(X)_{\chi_B}} \sqrt{Todd} \in HL \,,

where on the right we have the relative Todd class. This is the form the D-brane charge was originally found in the physics literature and in which it is still often given.

(In (BMRS2, Section 4) this is discussed for the untwisted case.)

For more general discussion see at Freed-Witten anomaly – Details as well as at Poincaré duality algebra – Properties – K-Orientation and Umkehr maps.

Via the Atiyah-Hirzebruch spectral sequence

The Atiyah-Hirzeburch spectral sequence expresses, starting from its $E_2$ pages, K-theory classes on spacetime $X$ as kernels of certain differential acting on ordinary cohomology in all even degrees (for type IIA strings) or all odd degrees (for type IIB strings)

E_2^{p,q} = H^p(X, KU^q(\ast)) \Rightarrow KU^\bullet(X) \,.

Discussion of D-brane charge this way is in (Maldacena-Moore-Seiberg 01, Evslin-Sati 06).

Related concepts

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D(-2)-brane	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G₂-manifold
topological M5-brane	$\,$	C6-field on G₂-manifold
S-brane
SM2-brane, membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

∞-Chern-Simons theory from binary and non-degenerate invariant polynomial

$n \in \mathbb{N}$	symplectic Lie n-algebroid	Lie integrated smooth ∞-groupoid = moduli ∞-stack of fields of $(n+1)$ -d sigma-model	higher symplectic geometry	$(n+1)$ d sigma-model	dg-Lagrangian submanifold/ real polarization leaf	= brane	(n+1)-module of quantum states in codimension $(n+1)$	discussed in:
0	symplectic manifold	symplectic manifold	symplectic geometry		Lagrangian submanifold	–	ordinary space of states (in geometric quantization)	geometric quantization
1	Poisson Lie algebroid	symplectic groupoid	2-plectic geometry	Poisson sigma-model	coisotropic submanifold (of underlying Poisson manifold)	brane of Poisson sigma-model	2-module = category of modules over strict deformation quantiized algebra of observables	extended geometric quantization of 2d Chern-Simons theory
2	Courant Lie 2-algebroid	symplectic 2-groupoid	3-plectic geometry	Courant sigma-model	Dirac structure	D-brane in type II geometry
$n$	symplectic Lie n-algebroid	symplectic n-groupoid	(n+1)-plectic geometry	$d = n+1$ AKSZ sigma-model

(adapted from Ševera 00)

References

General

The original article is

Joseph Polchinski, Dirichlet-Branes and Ramond-Ramond Charges, Phys. Rev. Lett. 75 (1995) 4724-4727 [arXiv:hep-th/9510017, doi:10.1103/PhysRevLett.75.4724]

from p.7:

although it appears that we have modified the type II theory by adding something new to it, we are now arguing that these objects are actually intrinsic to any nonperturbative formulation of the type II theory; presumably one should think of them as an alternate representation of the black $p$ -branes

General review:

Joseph Polchinski, TASI Lectures on D-Branes [arXiv:hep-th/9611050]
Clifford Johnson, Études on D-Branes, in: Mike Duff et. al. (eds.) Nonperturbative aspects of strings, branes and supersymmetry, Proceedings, Trieste, Italy, March 23-April 3, (1998) [arXiv:hep-th/9812196, spire:481393]
Koji Hashimoto, D-Brane – Superstrings and New Perspective of Our World, Springer 2012 (doi:10.1007/978-3-642-23574-0, spire:1188897)
Pietro Fre, The Branes: Three Viewpoints, In: Gravity, a Geometrical Course Springer 2013 (spire:1242195, doi:10.1007/978-94-007-5443-0_7)
Constantin Bachas, D-branes, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2311.18456, doi:10.1007/978-981-19-3079-9]

A classical text describing how the physics way to think of D-branes leads to seeing that they are objects in derived categories is

Paul Aspinwall, D-Branes on Calabi-Yau Manifolds (arXiv:hep-th/0403166)

Discussion with an eye towards string phenomenology is in

Luis Ibáñez, Angel Uranga, String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012

This can to a large extent be read as a dictionary from homological algebra terminology to that of D-brane physics.

More recent similar material with the emphasis on the K-theory aspects is

Richard Szabo, D-Branes and Bivariant K-Theory

Comments on the role of D-branes in mathematical physics and mathematics is in

Gregory Moore, The Impact of D-Branes on Mathematics (2014)

On orbifolds

Review includes

Frederik Roose, Strings and D-branes on orbifolds: from boundary states to geometry, 2001 (pdf)
Nikolas Prezas, Aspects of branes and orbifolds in string theory, 2002 (pdf, web)

See also the references at orientifold.

As higher super-GS-WZW type $\sigma$ -models

The Green-Schwarz sigma model with DBI action for D-branes is discussed in

Martin Cederwall, Alexander von Gussich, Bengt Nilsson, Per Sundell, Anders Westerberg, The Dirichlet Super-p-Branes in Ten-Dimensional Type IIA and IIB Supergravity, Nucl.Phys. B490 (1997) 179-201 (arXiv:hep-th/9611159)
Mina Aganagic, Jaemo Park, Costin Popescu, John Schwarz, Dual D-Brane Actions, Nucl. Phys. B496 (1997) 215-230 (arXiv:hep-th/9702133)

Discussion of Green-Schwarz action functionals for super D-branes and the interpretation of the WZW cocycles for the D-branes as cocycles on “extended super-Minkowski spacetime” is due to

C. Chrysso‌malakos, José de Azcárraga, José M. Izquierdo, C. Pérez Bueno, The geometry of branes and extended superspaces, Nucl. Phys. B 567 (2000) 293-330 [arXiv:hep-th/9904137, doi:10.1016/S0550-3213(99)00512-X]
Makoto Sakaguchi, IIB-Branes and New Spacetime Superalgebras, JHEP 0004 (2000) 019 (arXiv:hep-th/9909143)
José de Azcárraga, J. M. Izquierdo, Superalgebra cohomology, the geometry of extended superspaces and superbranes (arXiv:hep-th/0105125)

A corresponding discussion as ∞-Wess-Zumino-Witten theory and refinement of the brane scan to a “brane bouquet” of super L-∞ algebra extensions (hence in infinity-Lie theory via ∞-Wess-Zumino-Witten theory) is discussed in

Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields, International Journal of Geometric Methods in Modern Physics Volume 12, Issue 02 (2015) 1550018 (arXiv:1308.5264)
Domenico Fiorenza, Hisham Sati, Urs Schreiber The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory and type IIA string theory (arXiv:1606.03206)
Vincent Braunack-Mayer, Hisham Sati, Urs Schreiber, Gauge enhancement of Super M-Branes (arXiv:1806.01115)

D-brane charge quantization in topological K-theory

On the conjectural D-brane charge quantization in topological K-theory:

Origin and basics

The idea that D-branes have Dirac charge quantization in topological K-theory originates with the observation that their charge expressed in RR-field flux densities resembles the image of a Chern character:

Michael Green, Jeffrey A. Harvey, Gregory Moore, I-Brane Inflow and Anomalous Couplings on D-Branes, Class. Quant. Grav. 14 (1997) 47-52 $[$ arXiv:hep-th/9605033, doi:10.1088/0264-9381/14/1/008 $]$
Ruben Minasian, Gregory Moore, K-theory and Ramond-Ramond charge, JHEP 9711:002 (1997) $[$ arXiv:hep-th/9710230, doi:10.1088/1126-6708/1997/11/002 $]$

Further early discussion:

Edward Witten, D-Branes And K-Theory, JHEP 9812:019 (1998) [arXiv:hep-th/9810188, doi:10.1088/1126-6708/1998/12/019]
Petr Hořava, Type IIA D-Branes, K-Theory, and Matrix Theory (1998). (hep-th/9812135).
Daniel Freed, Michael Hopkins, On Ramond-Ramond fields and K-theory, JHEP 0005 (2000) 044 $[$ arXiv:hep-th/0002027, doi:10.1088/1126-6708/2000/05/044 $]$

and with emphasis on the full picture of twisted differential K-theory in:

Daniel Freed, Dirac charge quantization and generalized differential cohomology, Surveys in Differential Geometry, Int. Press, Somerville, MA, 2000, pp. 129–194 (arXiv:hep-th/0011220, doi:10.4310/SDG.2002.v7.n1.a6, spire:537392)

Here:

Green, Harvey & Moore (1997), Minasian & Moore (1997) observe that RR-field flux form-expressions for D-brane charge look like images of K-theory classes under the Chern character;

Witten 98, Section 3 adds the observation that the tachyon condensation – which is expected (this is Sen's conjecture from Sen 98) for open strings between D-brane/anti-D-branes – plausibly implements on their Chan-Paton vector bundles the defining equivalence relation (here) of topological K-theory.

Expression of these D-brane K-theory classes via the Atiyah-Hirzebruch spectral sequence:

Juan Maldacena, Gregory Moore, Nathan Seiberg, D-Brane Instantons and K-Theory Charges, JHEP 0111:062,2001 (arXiv:hep-th/0108100)
Jarah Evslin, Hisham Sati, Can D-Branes Wrap Nonrepresentable Cycles?, JHEP0610:050,2006 (arXiv:hep-th/0607045)

Specifically for D-branes in WZW models see

Peter Bouwknegt, A note on equality of algebraic and geometric D-brane charges in WZW models (pdf)

Understanding the solitonic (non-singular) D-branes and their T-duality in K-theory:

Oren Bergman, Eric G. Gimon, Petr Hořava, Brane Transfer Operations and T-Duality of Non-BPS States, JHEP 9904 (1999) 010 [doi:10.1088/1126-6708/1999/04/010, arXiv:hep-th/9902160]

Towards a matrix model taking these K-theoretic effects into account (K-matrix model):

Tsuguhiko Asakawa, Shigeki Sugimoto, Seiji Terashima, D-branes, Matrix Theory and K-homology, JHEP 0203 (2002) 034 $[$ arXiv:hep-th/0108085, doi:10.1088/1126-6708/2002/03/034 $]$

Twisted, equivariant and differential refinement

Discussion of charge quantization in twisted K-theory for the case of non-vanishing B-field:

Witten 98, Sec. 5.3 (for torsion twists)
Peter Bouwknegt, Varghese Mathai, D-branes, B-fields and twisted K-theory, Int. J. Mod. Phys. A 16 (2001) 693-706 $[$ arXiv:hep-th/0002023, doi:10.1088/1126-6708/2000/03/007 $]$

An elaborate proposal for the correct flavour of equivariant KR-theory needed for orientifolds is sketched in:

Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)

Discussion of full-blown twisted differential K-theory and its relation to D-brane charge in type II string theory

Daniel Grady, Hisham Sati, Ramond-Ramond fields and twisted differential K-theory, Advances in Theoretical and Mathematical Physics 26 5 (2022) $[$ doi:10.4310/ATMP.2022.v26.n5.a2, arXiv:1903.08843 $]$

Discussion of full-blown twisted differential orthogonal K-theory and its relation to D-brane charge in type I string theory (on orientifolds):

Daniel Grady, Hisham Sati, Twisted differential KO-theory (arXiv:1905.09085)

Reviews

Kasper Olsen, Richard Szabo, Brane Descent Relations in K-theory, Nucl.Phys. B566 (2000) 562-598 (arXiv:hep-th/9904153)
Kasper Olsen, Richard Szabo, Constructing D-Branes from K-Theory, Adv. Theor. Math. Phys. 3 (1999) 889-1025 (arXiv:hep-th/9907140)
John Schwarz, TASI Lectures on Non-BPS D-Brane Systems (arXiv:hep-th/9908144)
Edward Witten, Overview Of K-Theory Applied To Strings, Int. J. Mod. Phys. A16:693-706, 2001 (arXiv:hep-th/0007175)
Greg Moore, K-Theory from a physical perspective, in: Ulrike Tillmann (ed.) Topology, Geometry and Quantum Field Theory, Proceedings of the 2002 Oxford Symposium in Honour of the 60th Birthday of Graeme Segal, Cambridge University Press (2004) (arXiv:hep-th/0304018, doi:10.1017/CBO9780511526398.011)
Juan José Manjarín, Topics on D-brane charges with B-fields, Int. J. Geom. Meth. Mod. Phys. 1 (2004) (arXiv:hep-th/0405074)
Jarah Evslin, What Does(n’t) K-theory Classify?, Modave Summer School in Mathematical Physics (arXiv:hep-th/0610328, spire:730502)
Stefan Fredenhagen, Physical Background to the K-Theory Classification of D-Branes: Introduction and References (doi:10.1007/978-3-540-74956-1_1), chapter in: Dale Husemoeller, Michael Joachim, Branislav Jurčo, Martin Schottenloher, Basic Bundle Theory and K-Cohomology Invariants, Lecture Notes in Physics, Springer (2008) 1-9 $[$ doi:10.1007/978-3-540-74956-1, pdf $]$
Fabio Ruffino, Topics on topology and superstring theory (arXiv:0910.4524)
Hisham Sati, Urs Schreiber: Flux Quantization, in Encyclopedia of Mathematical Physics 2nd ed, Elsevier (2024) [arXiv:2402.18473]

Amplification of torsion-charges implied by charge quantization in Ktheory

Volker Braun, K-Theory Torsion [arXiv:hep-th/0005103]
Ilka Brunner, Jacques Distler, Torsion D-Branes in Nongeometrical Phases, Adv. Theor. Math. Phys. 5 (2002) 265-309 [doi:10.4310/ATMP.2001.v5.n2.a3, arXiv:hep-th/0102018]
Ilka Brunner, Jacques Distler, Rahul Mahajan, Return of the Torsion D-Branes, Adv. Theor. Math. Phys. 5 (2002) 311-352 [doi:10.4310/ATMP.2001.v5.n2.a4, arXiv:hep-th/0106262]

Review of D-branes charge seen in KK-theory:

Richard Szabo, D-branes and bivariant K-theory, Noncommutative Geometry and Physics 3 1 (2013): 131. (arXiv:0809.3029)

based on

Rui Reis, Richard Szabo, Geometric K-Homology of Flat D-Branes , Commun. Math. Phys. 266 (2006) 71-122 [arXiv:hep-th/0507043]
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-Branes, RR-Fields and Duality on Noncommutative Manifolds, Commun. Math. Phys. 277 (2008) 643-706 $[$ arXiv:hep-th/0607020, doi:10.1007/s00220-007-0396-y $]$
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, Noncommutative correspondences, duality and D-branes in bivariant K-theory, Adv. Theor. Math. Phys. 13:497-552, 2009 (arXiv:0708.2648)
Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-branes, KK-theory and duality on noncommutative spaces, J. Phys. Conf. Ser. 103 012004 (2008) $[$ arXiv:0709.2128, doi:10.1088/1742-6596/103/1/012004 $]$

In particular (BMRS2) discusses the definition and construction of D-brane charge as a generalized index in KK-theory. The discussion there focuses on the untwisted case. Comments on the generalization of this to topologicall non-trivial B-field and hence twisted K-theory is in

Richard Szabo, D-Branes, Tachyons and K-Homology, Mod. Phys. Lett. A17 (2002) 2297-2316 (arXiv:hep-th/0209210)

Conceptual problems

But there remain conceptual issues with the proposal that D-brane charge is in K-theory, as highlighted in

Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, section 4.5.2 and 4.6.5 of Triples, Fluxes, and Strings, Adv. Theor. Math. Phys. 4 (2002) 995-1186 [arXiv:hep-th/0103170, pdf]
Jarah Evslin, section 8 of: What Does(n’t) K-theory Classify?, Second Modave Summer School in Mathematical Physics [arXiv:hep-th/0610328]

In particular, actual checks of the proposal that D-brane charge is given by K-theory, via concrete computation in boundary conformal field theory, have revealed some subtleties:

Stefan Fredenhagen, Thomas Quella, Generalised permutation branes, JHEP 0511:004 (2005) [arXiv:hep-th/0509153, doi:10.1088/1126-6708/2005/11/004]

It might surprise that despite all the progress that has been made in understanding branes on group manifolds, there are usually not enough D-branes known to explain the whole charge group predicted by (twisted) K-theory. […] it is fair to say that a satisfactory answer is still missing.

The closest available towards an actual check of the argument for K-theory via open superstring tachyon condensation (Witten 98, Section 3) seems to be

Theodore Erler, Analytic Solution for Tachyon Condensation in Berkovits’ Open Superstring Field Theory, JHEP 1311 (2013) 007 [doi:10.1007/JHEP11(2013)007, arXiv:1308.4400]

which, however, concludes (on p. 32) with:

It would also be interesting to see if these developments can shed light on the long-speculated relation between string field theory and the K-theoretic description of D-brane charge $[$ 75, 76, 77 $]$ . We leave these questions for future work.

For orbifolds in equivariant K-theory

The proposal that D-brane charge on orbifolds is measured in equivariant K-theory (orbifold K-theory) goes back to

Witten 98, section 5.1

It was pointed out that only a subgroup of equivariant K-theory can be physically relevant in

Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, around (137) of: Triples, Fluxes, and Strings, Adv.Theor.Math.Phys. 4 (2002) 995-1186 (arXiv:hep-th/0103170)

Further discussion of equivariant K-theory for D-branes on orbifolds includes the following:

Hugo García-Compeán, D-branes in orbifold singularities and equivariant K-theory, Nucl.Phys. B557 (1999) 480-504 (arXiv:hep-th/9812226)
Matthias Gaberdiel, Bogdan Stefanski, Dirichlet Branes on Orbifolds, Nucl.Phys.B578:58-84, 2000 (arXiv:hep-th/9910109)
Igor Kriz, Leopoldo A. Pando Zayas, Norma Quiroz, Comments on D-branes on Orbifolds and K-theory, Int. J. Mod. Phys. A 23 (2008) 933-974 [arXiv:hep-th/0703122]
Richard Szabo, Alessandro Valentino, Ramond-Ramond Fields, Fractional Branes and Orbifold Differential K-Theory, Commun.Math.Phys.294:647-702, 2010 (arXiv:0710.2773)

Discussion of real K-theory for D-branes on orientifolds includes the following:

The original observation that D-brane charge for orientifolds should be in KR-theory is due to

Witten 98, section 5

and was then re-amplified in

Sergei Gukov, K-Theory, Reality, and Orientifolds, Commun.Math.Phys. 210 (2000) 621-639 (arXiv:hep-th/9901042)
Oren Bergman, E. Gimon, Shigeki Sugimoto, Orientifolds, RR Torsion, and K-theory, JHEP 0105:047, 2001 (arXiv:hep-th/0103183)

With further developments in

Varghese Mathai, Michael Murray, Daniel Stevenson, Type I D-branes in an H-flux and twisted KO-theory, JHEP 0311 (2003) 053 (arXiv:hep-th/0310164)

Discussion of orbi-orienti-folds using equivariant KO-theory is in

N. Quiroz, Bogdan Stefanski, Dirichlet Branes on Orientifolds, Phys.Rev. D66 (2002) 026002 (arXiv:hep-th/0110041)
Volker Braun, Bogdan Stefanski, Orientifolds and K-theory (arXiv:hep-th/0206158)
H. Garcia-Compean, W. Herrera-Suarez, B. A. Itza-Ortiz, O. Loaiza-Brito, D-Branes in Orientifolds and Orbifolds and Kasparov KK-Theory, JHEP 0812:007, 2008 (arXiv:0809.4238)

Discussion of the alleged K-theory classification of D-brane charge in relation to the M-theory C-field is in

Duiliu-Emanuel Diaconescu, Gregory Moore, Edward Witten, $E_8$ Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv.Theor.Math.Phys.6:1031-1134,2003 (arXiv:hep-th/0005090), summarised in A Derivation of K-Theory from M-Theory (arXiv:hep-th/0005091)

Entropy

The entropy of D-branes scales with the square of their number:

Around equation (3) in

Steven Gubser, Igor Klebanov Arkady Tseytlin, Coupling Constant Dependence in the Thermodynamics of $N = 4$ Supersymmetric Yang-Mills Theory, Nucl. Phys. B534:202-222, 1998 (arXiv:hep-th/9805156)

Around (3) in:

Igor Klebanov, From Threebranes to Large $N$ Gauge Theories (arXiv:hep-th/9901018)

Around equation (5.5) in:

Elias Kiritsis, T.R. Taylor, Thermodynamics of D-brane Probes (arXiv:hep-th/9906048)

For rational CFT

For exhaustive details on D-branes in 2-dimensional rational CFT see the references given at

FFRS-formalism

Branes within branes

Michael Douglas, Branes within Branes (arXiv:hep-th/9512077)

For topological strings

A discussion of topological D-branes in the context of higher category theory is in

Anton Kapustin, Topological Field Theory, Higher Categories, and Their Applications (arXiv:1004.2307)

Open string worldsheet Anomaly cancellation

The need for twisted spin^c structures as quantum anomaly-cancellaton condition on the worldvolume of D-branes was first discussed in

Daniel Freed, Edward Witten, Anomalies in String Theory with D-Branes (arXiv:hep-th/9907189)

More details are in

Anton Kapustin, D-branes in a topologically nontrivial B-field , Adv. Theor. Math. Phys.
4, no. 1, pp. 127–154 (2000), (arXiv:hep-th/9909089)

A clean review is provided in

Kim Laine, Geometric and topological aspects of Type IIB D-branes (arXiv:0912.0460)

For more see at Freed-Witten anomaly cancellation.

Relation to Dirac structures

Tsuguhiko Asakawa, Shuhei Sasa, Satoshi Watamura, D-branes in Generalized Geometry and Dirac-Born-Infeld Action (arXiv:1206.6964)

Last revised on May 27, 2024 at 05:59:49. See the history of this page for a list of all contributions to it.

nLab D-brane

Context

String theory

Ingredients

Critical string models

Extended objects

Topological strings

Backgrounds

Phenomenology

Contents

Idea

In 2d2d rational CFT

In 2d2d TFT

In terms of geometric data of the σ\sigma-model background

As black branes

Examples

Various dimensions

In the WZW model

Properties

As F-branes originating from M-branes

Characterization in terms of Dirac structures

D-brane charge

General

Via the Atiyah-Hirzebruch spectral sequence

Related concepts

References

General

On orbifolds

As higher super-GS-WZW type σ\sigma-models

D-brane charge quantization in topological K-theory

Origin and basics

Twisted, equivariant and differential refinement

Reviews

Conceptual problems

For orbifolds in equivariant K-theory

Entropy

For rational CFT

Branes within branes

For topological strings

Open string worldsheet Anomaly cancellation

Relation to Dirac structures

In $2d$ rational CFT

In $2d$ TFT

In terms of geometric data of the $\sigma$ -model background

As higher super-GS-WZW type $\sigma$ -models