nLab brane
Context
Quantum field theory
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Phyics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
This article is about the general concept of branes. For more specific details see also also at super p-brane, black brane and D-brane.
Contents
Idea
The term brane in formal high energy physics, and in particular in string theory, refers to entities that one thinks of as physical objects that generalize the notion point particles to higher dimensional objects.
The term derives from the word membrane that was originally used to describe 2-dimensional “particles”. When the need was felt to speak also about 3-, 4- and higher dimensional such “particles” the usage “3-brane”, “4-brane” etc. was introduced. Ordinary particles would be 0-branes in this counting, the strings in string theory would be 1-branes and membranes themselves 2-branes.
Generally, there are two different incarnations of branes
-
fundamental -branes (as in “fundamental particle”): these are given by sigma-models on -dimensional worldvolumes describing propagation of single -dimensional objects on certain target spacetimes. If these sigma-models are required to exhibit manifest target spacetime supersymmetry, then they are Green-Schwarz sigma models, which are classified by a “brane scan” in super L-infinity algebra cohomology;
-
black p-branes (as in “black hole”): these are solutions to field theories, typically supergravity theories, with singularities of dimension . In analogy to how a charged black hole () sources an electromagnetic field with field strength 2-form, so black -branes source -form higher gauge fields and hence appear in those supergravity theories where such exists.
The idea is that these two concepts match where a condensate of fundamental -branes turns into a black -brane.
Indeed, the classical no-hair theorem matches fundamental particles (i.e. 0-branes) characterized (via the Wigner classification) by just their mass, electromagnetic charge and angular momentum to black hole solutions of pure vacuum gravity. Accordingly, it is an old suggestion (Einstein-Infeld-Hoffmann 39) that fundamental particles could be identified with singular solutions of vacuum gravity.
This matching generalizes to higher dimensional -branes in higher dimensional supergravity and there is an exact correspondence between fundamental Green-Schwarz super p-branes and extremal BPS black brane solutions.
In string theory there is a third incarnation of branes, known as
- D-branes: these are the admissible boundary conditions for the 2-dimensional sigma models describing open strings.
One envisions that as one passes from perturbative string theory to the non-perturbative version of the theory (“M-theory”) these D-branes show back-reaction and turn into the UV-completion of the black branes seen in the supergravity effective field theory. This relation is key in the microscopic computation of black hole entropy for black holes in string theory.
Boundary conditions or D-branes
Some words on D-branes
In terms of the algebraic data of the QFT on the worldvolume
An abstractly defined -dimensional quantum field theory is a consistent assignment of state-space and correlators to -dimensional cobordisms with certain structure (topological structure, conformal structure, Riemannian structure, etc. see FQFT/AQFT). In an open-closed QFT the cobordisms are allowed to have boundaries. See at boundary field theory for more on this.
In this abstract formulation of QFT a brane is a type of data assigned by the QFT to boundaries of cobordisms.
In rational CFT
A well understood class of examples is this one: among all 2-dimensional conformal field theory, the case of full rational 2d CFT has been understood completely, using FFRS-formalism. It is then a theorem that full 2-rational CFTs are classified by
-
a modular tensor category (to be thought of as being the category of representations of the vertex operator algebra of the 2d CFT);
-
a special symmetric Frobenius algebra object internal to .
In this formulation a type of brane of the theory is precisely an -module in (an -bimodule is a bi-brane or defect line ):
the 2d cobordisms with boundary on which the theory defined by carry as extra structure on their connected boundary pieces a label given by an equivalence class of an -module in . The assignment of the CFT to such a cobordism with boundary is obtained by
-
triangulating the cobordism,
-
labeling all internal edges by
-
labelling all boundary pieces by the -module
-
all vertices where three internal edges meet by the multiplication operation
-
and all points where an internal edge hits a moundary by the corresponding action morphism
-
and finally evaluating the resulting string diagram in .
So in this abstract algebraic formulation of QFT on the worldvolume, a brane is just the datum assigned by the QFT to the boundary of a cobordism. But abstractly defined QFTs may arise from quantization of sigma models. This gives these boundary data a geometric interpretation in some space. This we discuss in the next section.
In TFT
Another case where the branes of a QFT are under good mathematical control is TCFT: the (infinity,1)-category-version of a 2d TQFT.
Particularly the A-model and the B-model are well understood.
-
the branes of the B-model (“B-branes”) form the the stable (infinity,1)-category of chain complexes of quasicoherent sheaves on the target space (often considered just in terms of its homotopy category of an (infinity,1)-category, the derived category of quasicoherent sheaves);
-
the branes of the A-model form the Fukaya category of the target space.
(…)
In terms of geometric data of the -model background
An abstractly defined QFT (as a consistent assignment of state spaces and propagators to cobordisms as in FQFT) may be obtained by quantization from geometric data :
Such a sigma-model QFT is the quantization of an action functional on a space of maps from a cobordism (“worldvolume”) to some target space that may carry further geometric data such as a Riemannian metric, or other background gauge fields.
One may therefore try to match the geometric data on that encodes the -model with the algebraic data of the FQFT that results after quantization. This gives a geometric interpretation to many of the otherwise purely abstract algebraic properties of the worldvolume QFT.
It turns out that if one checks which geometric data corresponds to the -modules in the above discussion, one finds that these tend to come from structures that look at least roughly like submanifolds of the target space . And typically these submanifolds themselves carry their own background gauge field data.
A well-understood case is the Wess-Zumino-Witten model: for this the target space is a simple Lie group and the background field is a circle 2-bundle with connection (a bundle gerbe) on , representing the background field that is known as the Kalb-Ramond field.
In this case it turns out that branes for the sigma model on are given in the simplest case by conjugacy classes inside the group, and that these carry a twisted vector bundle with the twist given by the Kalb-Ramond background bundle. These vector bundles are known in the string theory literature as Chan-Paton vector bundles . The geometric intuition is that a QFT with certain boundary condition comes from a quantization of spaces of maps that are restricted to take the boundary of to these submanifolds.
More generally, one finds that the geometric data that corresponds to the branes in the algebraically defined 2d QFT is given by cocycles in the twisted differential K-theory of . These may be quite far from having a direct interpretation as submanifolds of .
The case of rational 2d CFT considered so far is only the best understood of a long sequence of other examples. Here the collection of all D-branes – identified with the collection of all internal modules over an internal frobenius algebra, forms an ordinary category.
More generally, at least for 2-dimensional TQFTs analogous considerations yield not just categories but stable (∞,1)-categories of boundary condition objects. For instance for what is called the B-model 2-d TQFT the category of D-branes is the derived category of coherent sheaves on some Calabi-Yau space.
Starting with Kontsevich’s homological algebra reformulation of mirror symmetry the study of (derived) D-brane categories has become a field in its own right in pure mathematics.
… lots of further things to say …
Fundamental or -model branes
In string theory one speaks apart from the D-branes also about fundamental branes . These are the objects in the -dimensional sigma model themselves.
-
For this describes the ordinary quantum mechanics of a point particles on . And such point particles are the fundamental particles for instance of the standard model of particle physics.
-
For this describes the quantum propagation of a string, and accordingly one speaks of the fundamental string or F1-brane (fundamental 1-brane).
-
For this describes the quantum propagation of a membrane.
-
There are good indications that there is a way to describe heterotic string theory not in terms of fundamental 1-branes but in terms of the sigma-model of a fundamental 5-brane – the magnetic dual of the 1-brane in 10-dimensions.
-
etc.
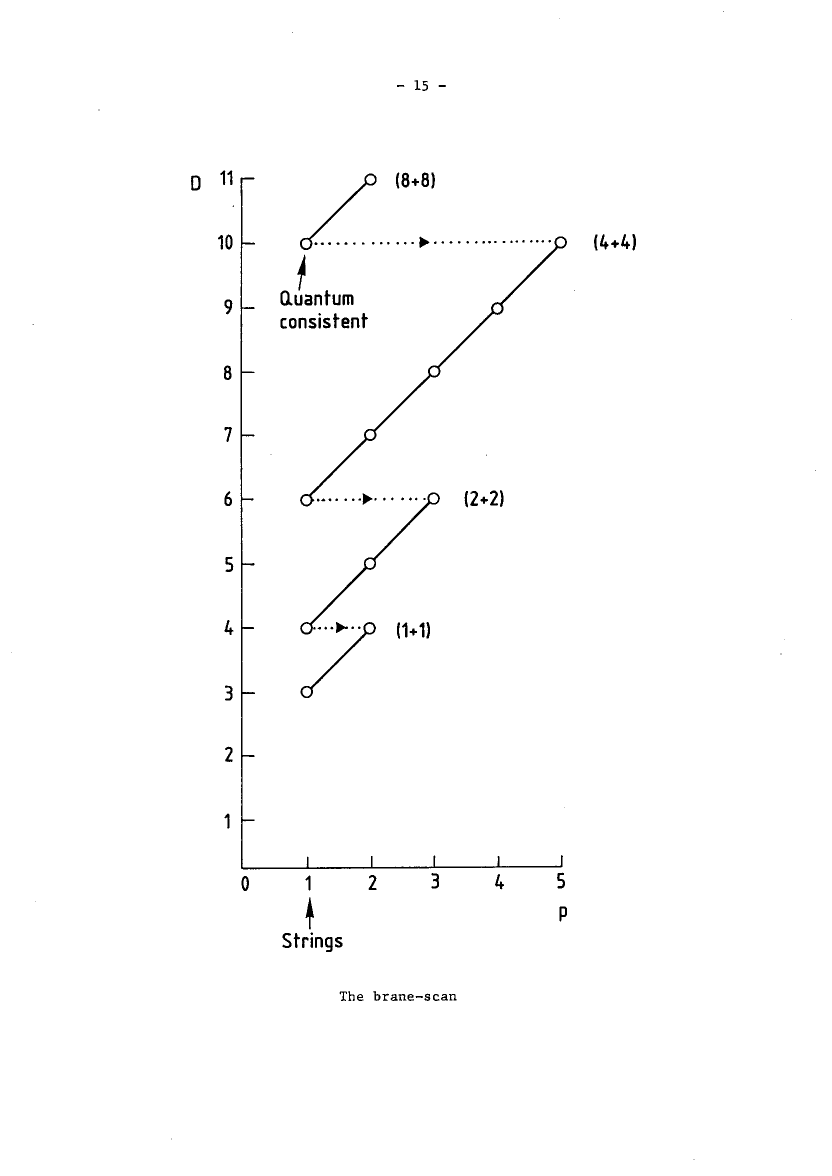
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
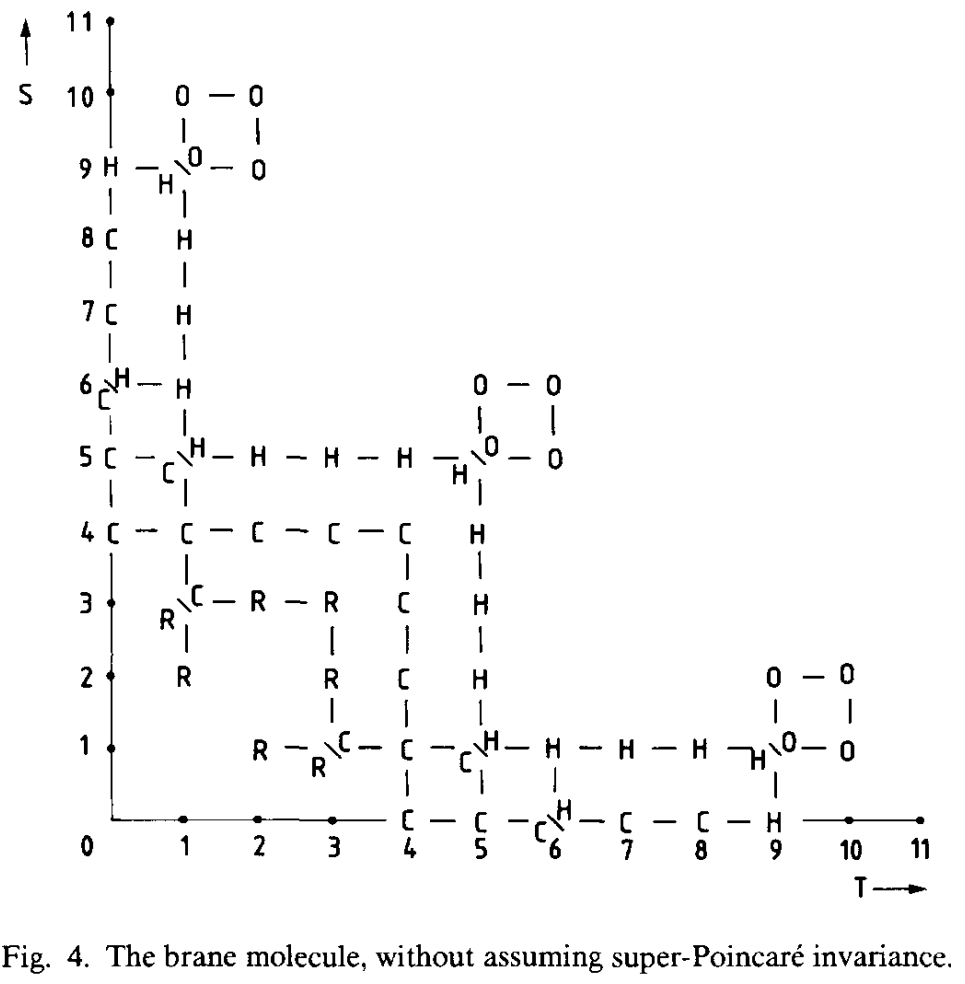
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
Black branes
See black brane.
Defect branes
See defect brane.
Exotic branes
See exotic brane.
Properties
Worldvolume theories
Table of branes appearing in supergravity/string theory (for classification see at brane scan).
The super-brane scan
If the worldvolume QFT of the fundamental branes (for instance the worldsheet 2dCFT of the string) is required to be a supersymmetric QFT?, specifically if the Green-Schwarz action functional is used only particular combinations of the dimension of the worldvolume and of spacetime are possible.
The corresponding table has been called the brane scan
Related concepts
| singularity | field theory with singularities |
|---|---|
| boundary condition/brane | boundary field theory |
| domain wall/bi-brane | QFT with defects |
∞-Chern-Simons theory from binary and non-degenerate invariant polynomial
(adapted from Ševera 00)
References
Prehistory
- Albert Einstein, Leopold Infeld, B. Hoffmann, The gravitational equations and the problem of motion, Annals of Mathematics, Vol 39, No. 1, 1938
See also
- Wikipedia, Black hole electron
The terminology “-brane” originates in
- Mike Duff, T. Inami, Christopher Pope, Ergin Sezgin, Kellogg Stelle, Semiclassical Quantization of the Supermembrane, Nucl.Phys. B297 (1988) 515-538 (spire:247064)
For more history see
- Mike Duff, Thirty years of Erice on the brane, Based on lectures at the International Schools of Subnuclear Physics 1987-2017 and the International Symposium “60 Years of Subnuclear Physics at Bologna”, University of Bologna, November 2018 (arXiv:1812.11658)
General
-
Pietro Fré, The Branes: Three Viewpoints, Chater 7 in: Gravity, a Geometrical Course, Springer (2013) [spire:1242195, doi:10.1007/978-94-007-5443-0_7]
-
Greg Moore, What is… a brane?, Notices of the AMS 52 2 (2005) [pdf]
-
Joan Simón, Brane Effective Actions, Kappa-Symmetry and Applications [arXiv:1110.2422]
-
Luis Ibáñez, Angel Uranga, section 6 of: String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press (2012)
Boundary conditions / D-branes
(…)
See D-brane.
For exhaustive details on D-branes in 2-dimensional rational CFT see the references given at
A classical text describing how the physics way to think of D-branes for the topological string leads to seeing that they are objects in derived categories (of coherent sheaves for the B-model) is reviewed in
- Paul Aspinwall, D-Branes on Calabi-Yau Manifolds (arXiv)
based on
-
Michael Douglas, D-branes, Categories and Supersymmetry, J.Math.Phys. 42 (2001) 2818-2843 (arXiv:hep-th/0011017)
-
Paul Aspinwall, Albion Lawrence, Derived Categories and Zero-Brane Stability (arXiv:hep-th/0104147)
This can to a large extent be read as a dictionary from homological algebra terminology to that of D-brane physics.
More recent similar material with the emphasis on the K-theory aspects is
Fundamental branes
The “brane scan” table showing the consistent dimension pairs for the Green-Schwarz action functional was depicted in
- Michael Duff, Supermembranes: the first fifteen weeks CERN-TH.4797/87 (scan)
going back to
- A. Achúcarro, J. M. Evans, Paul Townsend and D. L. Wiltshire, Super -branes Physics Letters B Volume 198, Issue 4, 3 (1987)
Further developments are in
More along these lines is in
- Michael Duff, S. Ferrara, Four curious supergravities (arXiv)
See also division algebras and supersymmetry.
Branes ending on branes
- Andrew Strominger, Open P-Branes, Phys. Lett. B383:44-47,1996 (arXiv:hep-th/9512059)
Last revised on July 1, 2023 at 15:13:46. See the history of this page for a list of all contributions to it.