nLab G₂ manifold
Context
Riemannian geometry
Contents
Idea
A -structure on a manifold of dimension 7 is a choice of G-structure on , for the exceptional Lie group G₂. Hence it is a reduction of the structure group of the frame bundle of along the canonical (the defining) inclusion into the general linear group.
Given that is the subgroup of the general linear group on the Cartesian space which preserves the associative 3-form on , a structure is a higher analog of an almost symplectic structure under lifting from symplectic geometry to 2-plectic geometry (Ibort).
A -manifold is a manifold equipped with -structure that is integrable to first order, i.e. torsion-free (prop. below). This is equivalently a Riemannian manifold of dimension 7 with special holonomy group being the exceptional Lie group G₂.
-manifolds may be understood as 7-dimensional analogs of real 6-dimensional Calabi-Yau manifolds. Accordingly the relation between Calabi-Yau manifolds and supersymmetry lifts from string theory to M-theory on G₂-manifolds.
Definition
The definition of -manifold stuctures proceeds in stages:
and then there are
-structure
Definition
For a smooth manifold of dimension a -structure on is a G-structure for G2 .
Remark
Since the inclusion of into factors through (see here), a -structure induces an orthogonal structure, hence a Riemannian metric.
Given the definition of G₂ as the stabilizer group of the associative 3-form on , there is accordingly an equivalent formulation of def. in terms of differential forms:
Definition
Write for the orbit of the associative 3-form under the canonical -action. Similarly for a smooth manifold of dimension 7, write
for the subset of the set of differential 3-forms on those that, as sections to the exterior power of the cotangent bundle, are pointwise in .
These are also called the positive forms (Joyce 00, p. 243) or the definite differential forms (Bryant 05, section 3.1.1) on .
(e.g. Bryant 05, definition 2)
Proposition
A -structure on , def. , is equivalently a choice of definite 3-form on , def. .
(e.g. Joyce 00, p. 243, Bryant 05, section 3.1.1)
Often it is useful to exhibit prop. in the following way.
Example
For a smooth manifold of dimension 7, write for its frame bundle. By the discussion at vielbein – in terms of basic forms on the frame bundle there is a universal -valued differential form on the total space of the frame bundle
(whose components we write ) such that given an orthogonal structure and a local section of orthogonal frames, then the pullback of differential forms
is the corresponding local vielbein field. Hence one obtains a universal 3-form on the frame bundle by setting
with the canonical components of the associative 3-form and with summation over repeated indices understood.
By construction this is such that on a chart any definite 3-form, def. , restricts to the pullback of via a section and hence is of the form
Conversely, given a 3-form such that on an atlas over which the frame bundle trivializes it is of this form
then the -valued transition functions of the given local trivialization must factor through and hence exhibit a -structure: because we have and hence
But by the nature of the universal vielbein, its local pullbacks are related by
i.e.
and hence (1) says that
which is precisely the defining condition for to take values in .
Viewed this way, the definite 3-forms characterizing -structures are an example of a more general kind of differential forms obtained from a constant form on some linear model space by locally contracting with a vielbein field. For instance on a super-spacetime solving the equations of motion of 11-dimensional supergravity there is a super-4-form part of the field strength of the supergravity C-field which is constrained to be locally of the form
for the super-vielbein. See at Green-Schwarz action functional – Membrane in 11d SuGra Background. Indeed, by the discussion there this 4-form is required to be covariantly constant, which is precisely the analog of -manifold structure as in def. .
References that write definite 3-forms in this form locally as include (BGGG 01 (2.9), …).
The following is important for the analysis:
Remark
The subset in def. is an open subset, hence is a stable form (e.g. Hitchin, def. 1.1).
(e.g. Joyce 00, p. 243, Bryant 05, 2.8)
Proof
By definition of as the stabilizer group of the associative 3-form, the orbit it generates under the -action is the coset . The dimension of this as a smooth manifold is 49-14 = 35. This is however already the full dimension of the space of 3-forms in 7d that the orbit sits in. Therefore (since does not have a boundary) the orbit must be an open subset.
Closed -structure
Definition
A -structure, def. , is called closed if the definite 3-form corresponding to it via prop. is a closed differential form, .
(e.g. Bryant 05, (4.31))
Proposition
For a closed -structure, def. , on a manifold there exists an atlas by open subsets
such that the globally defined 3-form is locally gauge equivalent to the canonical associative 3-form
via a 2-form on .
(e.g. Bryant 05, p. 21)
This follows from the fact, remark , that the definite 3-forms are an open subset inside all 3-forms: given a chart centered around any point then there is with vanishing at that point such that at that point. But since the -action on is open, there is an open neighbourhood around that point where this is still the case.
Remark
When regarding smooth manifolds in the wider context of higher differential geometry, then the situation of prop. corresponds to a diagram of formal smooth infinity-groupoids of the following form:
where is the higher moduli stack of flat 3-forms with 2-form gauge transformations between them (and 1-form gauge transformation between these). The diagram expresses the 3-form as a map to this moduli stack, which when restricted to the cover becomes gauge equivalent to the pullback of the associative 3-form , similarly regarded as a map, to the cover, where the gauge equivalence is exhibited by a homotopy (of maps of formal smooth -groupoids) which is the 2-form on .
-holonomy / -manifold
Definition/Proposition
A manifold equipped with a -structure, def. , is called a -manifold if the following equivalent conditions hold
-
we have
-
(closed)
-
(co-closed);
-
-
;
-
has special holonomy ;
-
(vanishing Ricci curvature);
-
(vanishing scalar curvature);
-
(vanishing torsion of the G2-structure).
Here
-
is the de Rham differential;
-
is the 3-form corresponding to the given -structure via prop. ;
-
is the induced Riemannian metric, via remark ;
-
is the Hodge star operator of this metric;
-
is the covariant derivative of this metric;
For the equivalence of the first items see for instance Joyce 96, p. 294 (4 of 38), Joyce 00, prop. 10.1.3. For the equivalence to the vanishing curvature invariant see also Bryant 05, corollary 1, and for the equivalence to the vanishing torsion of a G-structure see Bryant 05, prop. 2.
Remark
The higher torsion invariants of -structures do not necessarily vanish (contrary to the case for instance of symplectic structure and complex structure, see at integrability of G-structures – Examples). Therefore, even in view of prop. , a -manifold, def. , does not, in general admit an atlas by adapted coordinate charts equal to .
The space of second order torsion invariants of -structures is discussed by Bryant 05 (4.7).
Variants and weakenings
There are several variants of the definition of -manifolds, def., given by imposing other constraints on the torsion.
On a kind of instantons on -manifolds:
- Mario Garcia-Fernandez, Jason D. Lotay, Henrique N. Sá Earp, Agnaldo A. da Silva Jr.: Coupled -instantons [arXiv:2404.12937]
With skew-symmetric torsion
Discussion for totally skew symmetric torsion of a Cartan connection includes Friedrich & Ivanov 01, theorem 4.7, theorem 4.8.
Weak -holonomy
Definition
A 7-dimensional manifold is said to be of weak -holonomy if it carries a 3-form with the relation of def. generalized to
and hence
(See for instance Bilal & Derendinger-Sfetsos 02Bilal & Metzger 03](#BilalMetzger03).)
With ADE orbifold structure
When used as KK-compactification-fibers for M-theory on G₂-manifolds, then for quadi-realistic phenomenology one needs to consider ADE orbifolds with “-manifold” structure, i.e. G₂-orbifolds, also called Joyce orbifolds. Moreover, for F-theory purposes this -orbifold is to be a fibration by a K3 surface .
For instance, the Cartesian product admits a -manifold structure. There is a canonical SO(3)-action on the tangent spaces of , given on by rotation of the hyper-Kähler manifold-structure of and on by the standard rotation. For a finite subgroup of , hence a finite group in the ADE classification, then is a G₂-orbifold (Acharya 1098, p.3). For not a cyclic group then this has precisely one parallel spinor.
In a local coordinate chart of by the orbifold locally looks like , where now is a finite subgroup of SU(2). Such local G₂-orbifolds are discussed in some detail by Atiyah & Witten 2001. Families of examples are constructed in Reidegeld 2015.
Codimension-4 ADE singularities in -manifolds are discussed by Acharya & Gukov 2004, section 5.1 and Barrett 2006.
Properties
Existence
Proposition
A 7-manifold admits a -structure, def. , precisely if it admits an orientation and a spin structure.
That orientability and spinnability is necessary follows directly from the fact that is connected and simply connected. That these conditions are already sufficient is due to (Gray 69), see also (Bryant 05, remark 3).
Metric structure
The canonical Riemannian metric manifold is Ricci flat. More generally a manifold of weak -holonomy, def. , with weakness parameter is an Einstein manifold with cosmological constant .
As part of the Berger classification
classification of special holonomy manifolds by Berger's theorem:
As -Riemannian manifolds
(Leung 02)
As exceptional geometry
Spin(8)-subgroups and reductions to exceptional geometry
see also: coset space structure on n-spheres
Examples
Metric cones
The metric cone over complex projective 3-space carries the structure of a G₂-manifold whose Riemannian metric is invariant under the canonical Sp(2) action by left-matrix multiplication on homomogeneous coordinates in (Byant-Salamon 89, see also Acharya-Bryant-Salamon 20).
Resolution of Joyce orbifolds
by resolution of singularities in compact flat orbifolds
(…)
Twisted connected sum construction
by twisted connected sum-constructions
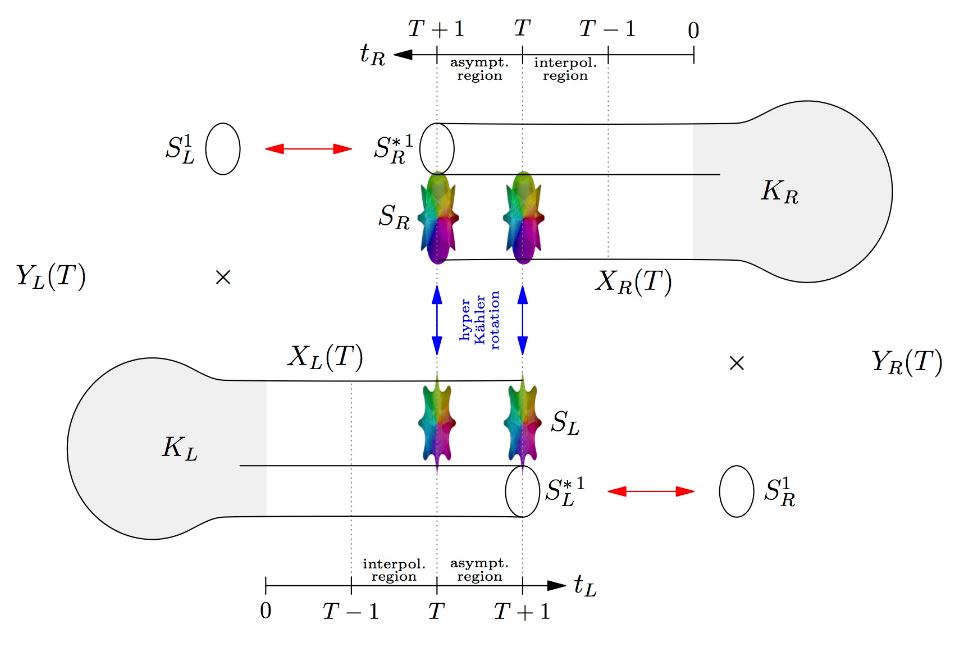
graphics grabbed from Klemm 16
Applications
In supergravity
In string phenomenology models obtained from compactification of 11-dimensional supergravity/M-theory on G₂-manifolds (see for instance Duff) can have attractive phenomenological properties, see for instance the G₂-MSSM.
Related concepts
References
General
General survey:
-
Spiro Karigiannis, What is… a -manifold (pdf)
-
Spiro Karigiannis, -manifolds – Exceptional structures in geometry arising from exceptional algebra (pdf)
-
Spiro Karigiannis, -Conifolds: A survey, 2014 (pdf)
-
Nigel Hitchin, Special holonomy and beyond, Clay Mathematics Proceedings (pdf)
-
Robert Bryant, Some remarks on -structures, Proceedings of the 12th Gökova Geometry-Topology Conference 2005, pp. 75-109 (arXiv:math/0305124, webpage, pdf)
The concept of -manifolds goes back to
- E. Bonan, (1966), Sur les variétés riemanniennes à groupe d’holonomie G2 ou Spin(7), C. R. Acad. Sci. Paris 262: 127–129.
Non-compact -manifolds were first constructed in
- Robert Bryant, Simon Salamon, On the construction of some complete metrics with exceptional holonomy, Duke Mathematical Journal 58: 829–850 (1989) (euclid:dmj/1077307681)
See also:
- Simon Salamon, Chapter 11 in: Riemannian Geometry and Holonomy Groups, Research Notes in Mathematics 201, Longman (1989)
Compact-manifolds were first found in:
-
Dominic Joyce, Compact Riemannian 7-manifolds with holonomy , Journal of Differential Geometry 43 2 (1996) [Euclid:jdg/1214458109]
-
Dominic Joyce, Compact manifolds with special holonomy, Oxford Mathematical Monographs (2000) [ISBN:9780198506010]
Review in:
-
Dominic Joyce, Compact Riemannian manifolds with exceptional holonomy, Surveys in Differential Geometry
Volume 6 (2001) (doi:10.4310/SDG.2001.v6.n1.a3)
The sufficiency of spin structure for -structure is due to:
- A. Gray, Vector cross products on manifolds, Trans. Amer. Math. Soc. 141 (1969), 465–504.
and the compact twisted connected sum G₂-manifolds due to:
- Alexei Kovalev, Twisted connected sums and special Riemannian holonomy, J. Reine Angew. Math. 565 (2003) (arXiv:math/0012189)
Review includes
- Alexei Kovalev, Constructions of compact -holonomy manifolds, in: Lectures and Surveys on -Manifolds and Related Topics, Springer (2020) [arXiv:1909.11473, doi:10.1007/978-1-0716-0577-6_2]
and from the point of view of M-theory on G₂-manifolds:
- Albrecht Klemm, Effective Action from M-theory on twisted connected sums, talk at Ascona Monte Verita, 6 July 2017 (pdf)
More compact examples are constructed in
- Dominic Joyce, Spiro Karigiannis, A new construction of compact -manifolds by gluing families of Eguchi-Hanson spaces [arXiv:1707.09325]
The relation to multisymplectic geometry/2-plectic geometry is mentioned explicitly in
- Alberto Ibort, Multisymplectic geometry: generic and exceptional, Proceedings of the IX Fall workshop on geometry and physics [pdf]
(but beware of some mistakes in that article)
For more see the references at exceptional geometry.
On -manifolds via , SYM inspired from M-theory on -manifolds:
- Andreas P. Braun, Evyatar Sabag, Matteo Sacchi, Sakura Schäfer-Nameki: -Manifolds from Theories, Part I: Domain Walls [arXiv:2304.01193]
-conifolds
On G₂-conifolds (G₂-manifolds with conical singularities):
Survey:
-
Spiro Karigiannis, -conifolds: A survey, 2014 (pdf)
-
Mark Haskins, Exotic Einstein metrics on and nearly Kähler 6-manifolds and -holonomy cones, 2016 (pdf)
Three simply connected -cones are known: the
-
metric cone on
-
metric cone on
-
Robert Bryant, Simon Salamon, On the construction of some complete metrics with exceptional holonomy, Duke Math. J. Volume 58, Number 3 (1989), 829-850 (euclid:euclid.dmj/1077307681)
-
Gary Gibbons, Don Page, Christopher Pope, Einstein metrics on , and bundles, Comm. Math. Phys. Volume 127, Number 3 (1990), 529-553 (euclid:cmp/1104180218)
More on the metric cone over complex projective 3-space as a G₂-manifold:
- Bobby Acharya, Robert Bryant, Simon Salamon, A circle quotient of a cone, Differential Geometry and its Applications Volume 73, December 2020, 101681 (arXiv:1910.09518, doi:10.1016/j.difgeo.2020.101681)
-Orbifolds
Discussion of G₂-orbifolds includes
-
Bobby Acharya, M theory, Joyce Orbifolds and Super Yang-Mills, Adv.Theor.Math.Phys. 3 (1999) 227-248 (arXiv:hep-th/9812205)
-
Michael Atiyah, Edward Witten -Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) (arXiv:hep-th/0107177)
-
Bobby Acharya, Sergei Gukov, M theory and Singularities of Exceptional Holonomy Manifolds, Phys.Rept.392:121-189,2004 (arXiv:hep-th/0409191)
-
Adam B. Barrett, M-Theory on Manifolds with Holonomy, 2006 (arXiv:hep-th/0612096)
-
Frank Reidegeld, -orbifolds from K3 surfaces with ADE-singularities (arXiv:1512.05114, spire:1409963, doi:10.17877/DE290R-18940)
-
Frank Reidegeld, K3 surfaces with a pair of commuting non-symplectic involutions (arXiv:1809.07501)
-
Bobby Acharya, Andreas Braun, Eirik Eik Svanes, Roberto Valandro, Counting Associatives in Compact Orbifolds (arXiv:1812.04008)
-
Daniel Platt, Existence of torsion-free -structures on resolutions of -orbifolds using weighted Hölder norms (arXiv:2011.00482)
Moduli
Discussion of the moduli space of -structures:
-
Sergey Grigorian, Shing-Tung Yau, Local geometry of the moduli space, Commun.Math.Phys.287:459-488,2009 (arXiv:0802.0723)
-
Spiro Karigiannis, Naichung Conan Leung, Hodge Theory for -manifolds: Intermediate Jacobians and Abel-Jacobi maps, Proceedings of the London Mathematical Society (3) 99, 297-325 (2009) [arXiv:0709.2987, talk slides pdf]
Relating to moduli of flat connections on tori:
- Bobby S. Acharya, Daniel A. Baldwin, Ricci Flat Metrics, Flat Connections and -Manifolds [arXiv:2312.12311]
Variants and generalizations
Discussion of the more general concept of Riemannian manifolds equipped with covariantly constant 3-forms is in
- Hông Vân Lê , Geometric structures associated with a simple Cartan 3-form, J. of Geometry and Physics 70 (2013) 205–223 arXiv:1103.1201
Relation to Killing spinors
Discussion of -structures in view of the existence of Killing spinors includes
- Thomas Friedrich, Stefan Ivanov, Parallel spinors and connections with skew-symmetric torsion in string theory, AsianJ.Math.6:303-336,2002 (arXiv:math/0102142)
Application in supergravity
The following references discuss the role of -manifolds in M-theory on G₂-manifolds:
- Mike Duff, M-theory on manifolds of holonomy: the first twenty years (arXiv:hep-th/0201062)
A survey of the corresponding string phenomenology for M-theory on G₂-manifolds (see there for more) is in
- Bobby Acharya, -manifolds at the CERN Large Hadron collider and in the Galaxy, talk at -days (2012) (pdf)
See also
- Andreas Brandhuber, Jaume Gomis, Steven Gubser, Sergei Gukov, Gauge Theory at Large N and New Holonomy Metrics, Nucl.Phys. B611 (2001) 179-204 (arXiv:hep-th/0106034)
Weak -holonomy is discussed in
-
Adel Bilal, J.-P. Derendinger, K. Sfetsos, (Weak) Holonomy from Self-duality, Flux and Supersymmetry, Nucl.Phys. B628 (2002) 112-132 (arXiv:hep-th/0111274)
-
Adel Bilal, Steffen Metzger, Compact weak -manifolds with conical singularities (arXiv:hep-th/0302021)
-
Thomas House, Andrei Micu, M-theory Compactifications on Manifolds with Structure (arXiv:hep-th/0412006)
For more on this see at M-theory on G₂-manifolds
Cohomology
An analysis of the de Rham complex of manifolds, and an analogue of Dolbeault cohomology is in
- Marisa Fernández, Luis Ugarte. Dolbeault Cohomology for -Manifolds. Geometriae Dedicata 70, 57–86 (1998). (doi)
Last revised on June 30, 2025 at 05:10:50. See the history of this page for a list of all contributions to it.