nLab M-theory on G₂-manifolds
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
The Kaluza-Klein reduction of 11-dimensional supergravity on G₂ manifolds (notably Freund-Rubin compactifications and variants) yields an effective 4-dimensional supergravity with gauge fields (arising from the KK-modes of the graviton) and charged fermions (arising from the KK-models of the gravitino). This construction is thought to lift to M-theory as the analog of the KK-compactification of heterotic string theory on Calabi-Yau manifolds (see at string phenomenology), and of F-theory on CY4-manifolds.
KK-compactifications of higher dimensional supergravity with minimal () supersymmetry:
| perspective | KK-compactification with supersymmetry |
|---|---|
| M-theory | M-theory on G₂-manifolds |
| F-theory | F-theory on CY4-manifolds |
| heterotic string theory | heterotic string theory on CY3-manifolds |
In order for this to yield phenomenologically interesting effective physics the compactification space must be a G₂-orbifold (hence a Riemannian orbifold of special holonomy), its stabilizer groups will encode the nonabelian gauge group of the effective theory by “geometric engineering of quantum field theory” (Acharya 98, Atiyah-Witten 01, section 6), see below. Specifically for discussion of string phenomenology obtaining or approximating the standard model of particle physics by this procedure see at G₂-MSSM.
Details
Vacuum solutions
Genuine G₂-manifold/orbifold fibers, these having vanishing Ricci curvature, correspond to vacuum solutions of the Einstein equations of 11d supergravity, i.e. with vanishing field strength of the gravitino and the supergravity C-field (see e.g. Acharya 02, p. 9). (If one includes non-vanishing -field strength one finds “weak -holonomy” instead, see below).
Notice that vanishing gravitino field strength (i.e. covariant derivative) means that the torsion of the super-vielbein is in each tangent space the canonical torsion of the super Minkowski spacetime. This torsion constraint already just for the bosonic part of the super-vielbein implies (together with the Bianchi identities) the equations of motion of supergravity, hence here the vacuum Einstein equations in the 11d spacetime.
Complexified moduli space
For vanishing field strength of the supergravity C-field, the formal linear combination
of the (flat) supergravity -field and the 3-form of the -structure is the natural holomorphic coordinate on the moduli space of the KK-compactification of a -manifold, in M-theoretic higher analogy of the complexified Kähler classes of CY compactifications of 10d string theory (Harvey-Moore 99, (2.7), Acharya 02, (32) (59) (74), Grigorian-Yau 08, (4.57), Acharya-Bobkov 08, (4)).
Notice that restricted to associative submanifolds this combination becomes , which also governs the membrane instanton-contributions (“complex volume”).
Nonabelian gauge groups and chiral fermions at orbifold singularities
The KK-compactification of vacuum 11-dimensional supergravity on a smooth G₂-manifold results in a effective N=1 D=4 super Yang-Mills theory with abelian gauge group and with complex scalar fields which are neutral (not charged) under this gauge group (with the Betti numbers of ) (e.g. Acharya 02, section 2.3). This is of course unsuitable for phenomenology.
But when is a -orbifold then:
-
at an ADE singularity there is enhanced gauge symmetry in that the gauge group (which a priori is copies of the abelian group of the supergravity C-field) becomes nonabelian (Acharya 98, Acharya 00, review includes Acharya 02, section 3, BBS 07, p. 422, 436, Ibáñez-Uranga 12, section 6.3.3, Wijnholt 14, part III (from which the graphics below is grabbed));
-
at a (non-orbifold) conical singularity chiral fermions appear (Witten 01, p. 3, Atiyah-Witten 01, Acharya-Witten 01, Berglund-Brandhuber 02, Bourjaily-Espahbodi 08).
| ADE-singularity | conical singularity |
|---|---|
| gauge enhancement | chiral fermions |
The conical singularities are supposed/assumed to be isolated (Witten 01, section 2), while the ADE singularities are supposed/assumed to be of codimension-4 in the 7-dimensional fibers (Witten 01, section 3, Barrett 06).
In the absence of a proper microscopic definition of M-theory, the first point is argued indirectly in at least these ways:
-
The fact that under KK-compactification to type IIA string theory the singularity becomes special points of intersecting D6-branes for which the gauge enhancement is folklore (Sen 97, Witten 01, p. 1, based on Cvetic-Shiu-Uranga 01).
-
The duality between M-theory compactified on K3 and heterotic string theory on a 3-torus (Acharya-Witten 01). Here it is fairly well understood that at the degeneration points of the K3-moduli space enhanced nonabelian gauge symmetry appears (e.g. Acharya-Gukov 04, section 5.1). This comes down (Intriligator-Seiberg 96) to the fact that an ADE singularity generically constitutes a point in the moduli space of vacua in the Higgs branch of a super Yang-Mills theory.
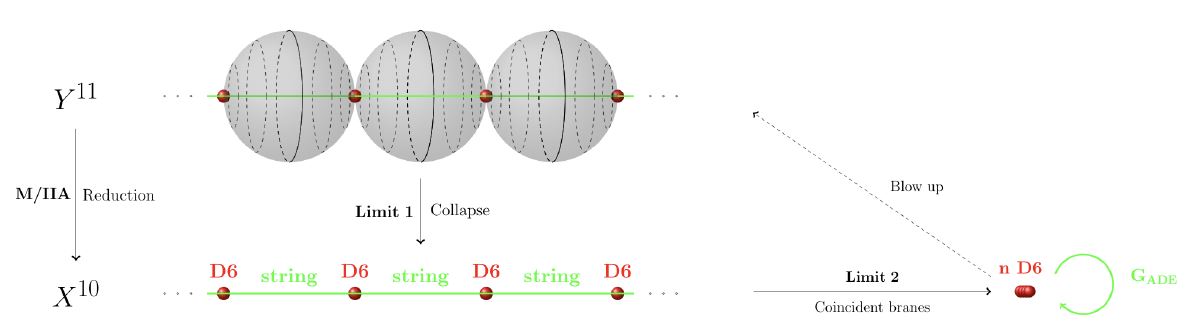
The blow-up of an ADE-singularity happens to be a union of 2-spheres touching pairwise in one point, such as to form the Dynkin diagram of the simple Lie group which under the ADE classification corresponds to the given orbifold isotropy group.
(graphics grabbed from HSS18)
M2-branes may wrap these 2-cycles and since before blow-up they are of vanishing size, this corresponds to double dimensional reduction under which the M2-branes become strings stretching between coincident D-branes. These are well-understood to be the quanta of nonabelian gauge Chan-Paton gauge fields located on the D-branes, and hence these same nonabelian degrees of freedom have had to be present already at the level of the M2-branes. This is due to (Sen 97), for more see at M-theory lift of gauge enhancement on D6-branes.
-
In the F-theory description the ADE singularity maps to the locus where the F-theory elliptic fibration degenerates with 2-cycles in the elliptic fibers shrinking to 0. Via double dimensional reduction this manifestly takes the M2-brane wrapping these elliptic fibers to an open string stretching between D7-branes. This yields at least gauge symmetry by the usual string theory argument about Chan-Paton gauge fields.
Also notice that at least the -enhancement of the effective field theory at -singularities matches the -enhancement of the worldvolume theory of -coincident M2-branes sitting at the orbifold singularity: this is the statement of the ABJM model.
Solutions with non-vanishing -field strength
Claim: There is no warped KK-compactification of M-theory on which retains at least supersymmetry in 4d while at the same time having non-vanishing -flux (field strength of the supergravity C-field). In other words, non-vanishing flux always breaks the supersymmetry.
e.g. (Acharya-Spence 00) see the Introduction of (Beasley-Witten 02)
In compactifications with weak G₂ holonomy it is the defining 4-form (the one which for strict G₂ manifolds is the Hodge dual of the associative 3-form) which is the flux/field strength of the supergravity C-field. See for instance (Bilal-Serendinger-Sfetos 02, section 6):
Consider a KK-compactification-Ansatz and
-
;
where , are given vielbein fields on and and is the Hodge dual of the associative 3-form. Then the Einstein equations of 11-dimensional supergravity give
(where , is the metric tensor) saying that both spaces are Einstein manifolds (BSS 02, (5.4)). The equations of motion for the supergravity C-field is
for the pullback of the associative 3-form (BSS 02, (5.5)), saying that exhibits weak G₂-holonomy with weakness parameter given by the component of the C-field on .
Confinement?
An idea for a strategy towards a proof of confinement in N=1 D=4 super Yang-Mills theory via two different but conjecturally equivalent realizations as M-theory on G₂-manifolds has been given in Atiyah-Witten 01, section 6, review is in Acharya-Gukov 04, section 5.3.
The idea here is to consider a KK-compactification of M-theory on fibers which are G₂-manifolds that locally around a special point are of the form
where
-
is a finite subgroup of SU(2) that acts canonically by left-multiplication on SU(2);
-
denotes the metric cone construction.
This means that is a smooth manifold, but , as soon as is not the trivial group, , is an orbifold with an ADE singularity.
Now the lore of M-theory on G₂-manifolds predicts that KK-compactification
-
on yields a 4d theory without massless fields (since there are no massless modes on the covering space of )
-
on the ADE-singularity yields non-abelian Yang-Mills theory in 4d coupled to chiral fermions.
both of these dual by thinking of them in two different ways as M-theory on the 8-manifold HP^2 (Atiyah-Witten 01, p. 75 onwards).
So in the first case a mass gap is manifest, while non-abelian gauge theory is not visible, while in the second case it is the other way around.
But if there were an argument that M-theory on G₂-manifolds is in fact equivalent for compactification both on and on . To the extent that this is true, it looks like an argument that could demonstrate confinement in non-abelian 4d gauge theory.
This approach is suggested in Atiyah-Witten 01, pages 84-85. An argument that this equivalence is indeed the case is then provided in sections 6.1-6.4, based on an argument in Atiyah-Maldacena-Vafa 00.
Relation to intersecting D-brane models
relation to intersecting D-brane models: see there
Related concepts
References
General
The first discussion of KK-compactification of 11d supergravity on fibers with G₂-holonomy is due to:
-
Moustafa A. Awada, Mike Duff, Christopher Pope, Supergravity Breaks Down to , Phys. Rev. Lett. 50 5 (1983) 294 [doi:10.1103/PhysRevLett.50.294]
-
Mike Duff, Bengt Nilsson, Christopher Pope, Spontaneous Supersymmetry Breaking by the Squashed Seven-Sphere, Phys. Rev. Lett. 50, 2043 (1983) (doi:10.1103/PhysRevLett.50.2043, erratum)
More generally, the KK-compactification of 11d supergravity of fibers of special holonomy was originally considered in
-
Edward Witten, Search for a realistic Kaluza-Klein theory, Nuclear Physics B Volume 186, Issue 3, 10 August 1981, Pages 412-428 (doi:10.1016/0550-3213(81)90021-3)
-
Leonardo Castellani, Riccardo D'Auria, Pietro Fré, chapter V.6 of Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)
-
George Papadopoulos, Paul Townsend, Compactification of D=11 supergravity on spaces of exceptional holonomy, Phys. Lett. B357:300-306,1995 (arXiv:hep-th/9506150)
Dedicated string phenomenology for the case of compactification on G₂-manifolds (or rather orbifolds) goes back to:
-
Bobby Acharya, M theory, Joyce Orbifolds and Super Yang-Mills, Adv. Theor. Math. Phys. 3 (1999) 227-248 [arXiv:hep-th/9812205]
-
Bobby Acharya, On Realising Super Yang-Mills in M theory (arXiv:hep-th/0011089)
-
Bobby Acharya, B. Spence, Flux, Supersymmetry and M theory on 7-manifolds (arXiv:hep-th/0007213)
-
Bobby Acharya, M Theory, -manifolds and four-dimensional physics, Classical and Quantum Gravity 19 22 (2002) [doi:10.1088/0264-9381/19/22/301, pdf]
-
Michael Atiyah, Juan Maldacena, Cumrun Vafa, An M-theory Flop as a Large Duality, J. Math. Phys. 42 (2001) 3209-3220 [arXiv:hep-th/0011256]
-
Sergei Gukov. Solitons, Superpotentials and Calibrations. Nuclear Physics B 574 1–2 (2000) 169-188. [doi:10.1016/S0550-3213(00)00053-5]
-
Chris Beasley, Edward Witten, A Note on Fluxes and Superpotentials in M-theory Compactifications on Manifolds of Holonomy, JHEP 0207:046,2002 (arXiv:hep-th/0203061)
-
Michael Atiyah, Edward Witten: -Theory dynamics on a manifold of -holonomy, Adv. Theor. Math. Phys. 6 (2001) [arXiv:hep-th/0107177, doi:10.4310/ATMP.2002.v6.n1.a1]
-
Edward Witten, Anomaly Cancellation On Manifolds Of Holonomy (arXiv:hep-th/0108165)
-
Bobby Acharya, Edward Witten, Chiral Fermions from Manifolds of Holonomy (arXiv:hep-th/0109152, spire:563029)
-
Per Berglund, Andreas Brandhuber, Matter from -manifolds, Nucl. Phys. B641 (2002) 351-375 (arXiv:hep-th/0205184)
-
Adam B. Barrett, M-Theory on Manifolds with Holonomy, 2006 (arXiv:hep-th/0612096)
-
Jacob L. Bourjaily, Sam Espahbodi, Geometrically Engineerable Chiral Matter in M-Theory (arXiv:0804.1132)
Expanding on Atiyah-Witten 01:
- Bobby Acharya, Lorenzo Foscolo, Marwan Najjar, Eirik Eik Svanes, New -conifolds in M-theory and their Field Theory Interpretation (arXiv:2011.06998)
See also:
-
Ashoke Sen, A Note on Enhanced Gauge Symmetries in M- and String Theory, JHEP 9709:001,1997 (arXiv:hep-th/9707123)
-
Mirjam Cvetic, Gary Gibbons, H. Lü and Christopher Pope, Supersymmetric M3-branes and Manifolds (pdf)
-
Bobby Acharya, F. Denef, C. Hofman, Neil Lambert, Freund-Rubin Revisited (arXiv:hep-th/0308046)
More discussion of the non-abelian gauge group enhancement at orbifold singularities includes
-
Mirjam Cvetic, Gary Shiu, Angel Uranga, Chiral Four-Dimensional Supersymmetric Type IIA Orientifolds from Intersecting D6-Branes, Nucl. Phys. B615:3-32,2001 (arXiv:hep-th/0107166)
-
James Halverson, David Morrison, On Gauge Enhancement and Singular Limits in Compactifications of M-theory, J. High Energ. Phys. 2016 100 (2016) [arXiv:1507.05965, doi:10.1007/JHEP04(2016)100]
-
Antonella Grassi, James Halverson, Julius L. Shaneson, Matter From Geometry Without Resolution,
High Energ. Phys. 2013 205 (2013) [arXiv:1306.1832, doi:10.1007/JHEP10(2013)205]
-
Neil Lambert, Miles Owen, Charged Chiral Fermions from M5-Branes (arXiv:1802.07766)
-
Andreas Braun, Sebastjan Cizel, Max Hubner, Sakura Schafer-Nameki, Higgs Bundles for M-theory on -Manifolds (arXiv:1812.06072)
-
Max Hubner, Local -Manifolds, Higgs Bundles and a Colored Quantum Mechanics (arXiv:2009.07136)
Discussion in relation to the duality between M-theory and heterotic string theory:
- Bobby Acharya, Alex Kinsella, David Morrison, Non-Perturbative Heterotic Duals of M-Theory on Orbifolds (arXiv:2106.03886)
Discussion of Freund-Rubin compactification on “with flux”, hence non-vanishing supergravity C-field and how they preserve one supersymmetry if is of weak G₂ holonomy with = cosmological constant = C-field strength on is in:
-
Adel Bilal, J.-P. Derendinger, K. Sfetsos, (Weak) Holonomy from Self-duality, Flux and Supersymmetry, Nucl.Phys. B628 (2002) 112-132 (arXiv:hep-th/0111274)
-
Thomas House, Andrei Micu, M-theory Compactifications on Manifolds with Structure (arXiv:hep-th/0412006)
Further discussion of membrane instantons in this context includes
- Gottfried Curio, Superpotentials for M-theory on a G2 holonomy manifold and Triality symmetry_, JHEP 0303:024,2003 (arXiv:hep-th/0212211)
Survey and further discussion includes
-
Michael Duff, M-theory on manifolds of holonomy: the first twenty years (arXiv:hep-th/0201062)
-
Sergei Gukov, M-theory on manifolds with exceptional holonomy, Fortschr. Phys. 51 (2003), 719–731 (pdf)
-
Bobby Acharya, Sergei Gukov, M theory and Singularities of Exceptional Holonomy Manifolds, Phys.Rept.392:121-189,2004 (arXiv:hep-th/0409191)
-
Adil Belhaj, M-theory on manifolds and the method of (p, q) brane webs, J. Phys. A: Math. Gen. 37 5067 (2004) [doi:10.1088/0305-4470/37/18/011^rbrack;
-
Adam B. Barrett, M-Theory on Manifolds with Holonomy (arXiv:hep-th/0612096)
-
James Halverson, David Morrison, The Landscape of M-theory Compactifications on Seven-Manifolds with Holonomy (arXiv:1412.4123)
-
Aaron Kennon, -Manifolds and M-Theory Compactifications (arXiv:1810.12659)
On the corresponding membrane instanton corrections to the superpotential?:
-
Jeffrey Harvey, Greg Moore, Superpotentials and Membrane Instantons (arXiv:hep-th/9907026)
-
Katrin Becker, Melanie Becker, John Schwarz, p. 333 of String Theory and M-Theory: A Modern Introduction, 2007
On duality with F-theory on CY4-manifolds:
-
Sergei Gukov, Shing-Tung Yau, Eric Zaslow, Duality and Fibrations on Manifolds (arXiv:hep-th/0203217)
-
Adil Belhaj, F-theory Duals of M-theory on Manifolds from Mirror Symmetry (arXiv:hep-th/0207208)
-
Mariana Graña, Carlos S. Shahbazi, Marco Zambon, -manifolds in compactifications to four dimensions, JHEP11 (2014) 046 [arXiv:1405.3698]
On duality with heterotic string theory on CY3-manifolds:
- Andreas Braun, Sakura Schäfer-Nameki, Compact, Singular -Holonomy Manifolds and M/Heterotic/F-Theory Duality, JHEP04 (2018) 126 (arXiv:1708.07215)
The moduli space is discussed in
-
Sergey Grigorian, Shing-Tung Yau, Local geometry of the moduli space, Commun. Math.Phys. 287 (2009) 459-488
-
Bobby Acharya, Konstantin Bobkov, Kähler Independence of the -MSSM, HEP 1009:001,2010 (arXiv:0810.3285)
-
Spiro Karigiannis, Naichung Conan Leung,Hodge Theory for -manifolds: Intermediate Jacobians and Abel-Jacobi maps_, Proceedings of the London Mathematical Society (3) 99, 297-325 (2009) (arXiv:0709.2987 talk slides pdf
On M-theory on times a weak -manifold:
- Vincent Van Hemelryck: Weak -manifolds and scale separation in M-theory from type IIA backgrounds [arXiv:2408.16609]
Phenomenology
Popular exposition of the G₂-MSSM phenomenology:
- Gordon Kane, String theory and the real world, Morgan & Claypool, 2017 (doi:0.1088/978-1-6817-4489-6)
Further discussion of string phenomenology in terms of -theory on -manifolds, beyond the original (Acharya 98, Atiyah-Witten 01, Acharya-Witten 01):
-
Bobby Acharya, Gordon Kane, Piyush Kumar, Compactified String Theories – Generic Predictions for Particle Physics, Int. J. Mod. Phys. A, Volume 27 (2012) 1230012 (arXiv:1204.2795)
-
Bobby Acharya, -manifolds at the CERN Large Hadron collider and in the Galaxy, talk at -days (2012) (pdf)
-
Gordon Kane, String/M-theories About Our World Are Testable in the traditional Physics Way (arXiv:1601.07511, video recording)
Discussion of moduli stabilization for stabilization via “flux” (non-vanishing bosonic field strength of the supergravity C-field) is in
- Bobby Acharya, A Moduli Fixing Mechanism in M theory (arXiv:hep-th/0212294)
and moduli stabilization for fluxless compactifications via nonperturbative effects, claimed to be sufficient and necessary to solve the hierarchy problem, is discussed in
-
Bobby Acharya, Konstantin Bobkov, Gordon Kane, Piyush Kumar, Diana Vaman, An M theory Solution to the Hierarchy Problem, Phys.Rev.Lett.97:191601,2006 (arXiv:hep-th/0606262)
-
Bobby Acharya, Konstantin Bobkov, Gordon Kane, Piyush Kumar, Jing Shao, Explaining the Electroweak Scale and Stabilizing Moduli in M Theory, Phys.Rev.D76:126010,2007 (arXiv:hep-th/0701034)
-
Bobby Acharya, Piyush Kumar, Konstantin Bobkov, Gordon Kane, Jing Shao, Scott Watson, Non-thermal Dark Matter and the Moduli Problem in String Frameworks,JHEP 0806:064,2008 (arXiv:0804.0863)
and specifically for the G₂-MSSM in
- Bobby Acharya, Konstantin Bobkov, Gordon Kane, Piyush Kumar, Jing Shao, The -MSSM - An Theory motivated model of Particle Physics (arXiv:0801.0478)
the strong CP problem is discussed in
-
Peter Svrcek, Edward Witten, section 6 of Axions In String Theory, JHEP 0606:051,2006 (arXiv:hep-th/0605206)
-
Bobby Acharya, Konstantin Bobkov, Piyush Kumar, An M Theory Solution to the Strong CP Problem and Constraints on the Axiverse, JHEP 1011:105,2010 (arXiv:1004.5138)
and realization of GUTs in
-
Edward Witten, Deconstruction, Holonomy, and Doublet-Triplet Splitting, (arXiv:hep-ph/0201018)
-
Bobby Acharya, Krzysztof Bozek, Miguel Crispim Romao, Stephen F. King, Chakrit Pongkitivanichkul, Grand Unification in M theory on a manifold (arXiv:1502.01727)
The phenomenology of compactifications on compact twisted connected sum G₂-manifolds (Kovalev 00) is in
- Thaisa C. da C. Guio, Hans Jockers, Albrecht Klemm, Hung-Yu Yeh, Effective action from M-theory on twisted connected sum -manifolds (arXiv:1702.05435, talk video)
Discussion of the cosmological constant in these models includes
- Beatriz de Carlos, Andre Lukas, Stephen Morris, Non-perturbative vacua for M-theory on manifolds, JHEP 0412:018, 2004 (arxiv:hep-th/0409255)
which concludes that with taking non-perturbative effects from membrane instantons into account one gets 4d vacua with vanishing and negative cosmological constant (Minkowski spacetime and anti-de Sitter spacetime) but not with positive cosmological constant (de Sitter spacetime). They close by speculating that M5-brane instantons might yield de Sitter spacetime.
Suggestion that higher curvature corrections allow de Sitter spacetime vacua:
- Johan Blåbäck, Ulf Danielsson, Giuseppe Dibitetto, Suvendu Giri, Constructing stable de Sitter in M-theory from higher curvature corrections (arXiv:1902.04053)
See also
- Andreas Braun, Sebastjan Cizel, Max Hubner, Sakura Schafer-Nameki, Higgs Bundles for M-theory on -Manifolds (arXiv:1812.06072)
Discussion of Yukawa couplings among 3 generations of fundamental fermions:
- Eric Gonzalez, Gordon Kane, Khoa Dang Nguyen, Malcolm Perry, Quark and lepton mass matrices from localization in M-theory on orbifold (arXiv:2002.11820)
On neutrino masses:
- Eric Gonzalez, Gordon Kane, Khoa Nguyen, Neutrino mass matrices from localization in M-theory on orbifold (arXiv:2107.12893)
Last revised on August 30, 2024 at 07:10:48. See the history of this page for a list of all contributions to it.