nLab 4T relation
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
For round chord diagrams
In knot theory by the 4-term relations or 4T-relations, for short, one means the following relations in the linear span of chord diagrams:
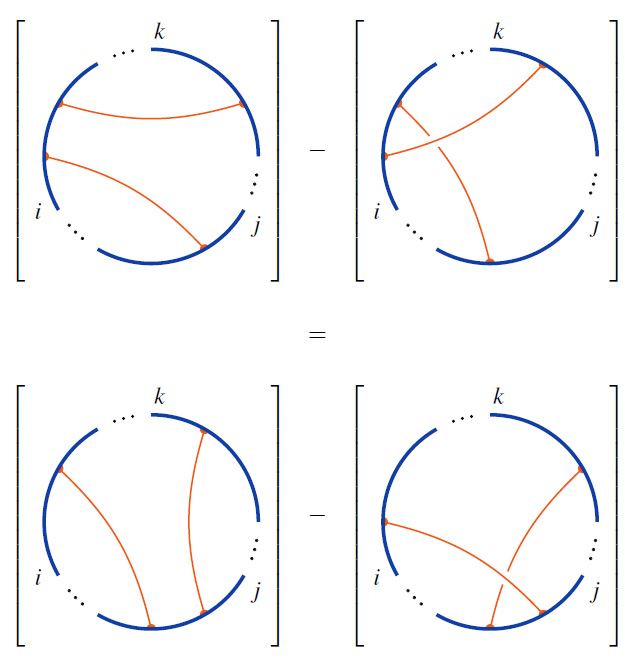
graphics from Sati-Schreiber 19c
These are the relations respected by weight systems on chord diagrams.
For horizontal chord diagrams
For horizontal chord diagrams the 4T relations is the following:
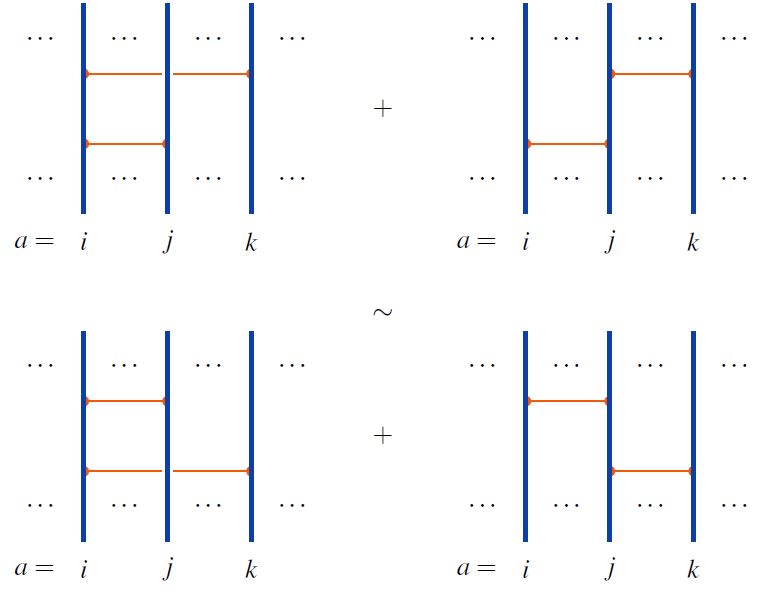
graphics from Sati-Schreiber 19c
When the linear span of horizontal chord diagrams is regarded as an associative algebra under concatenation of strands (here), this relation is the infinitesimal braid relation
Properties
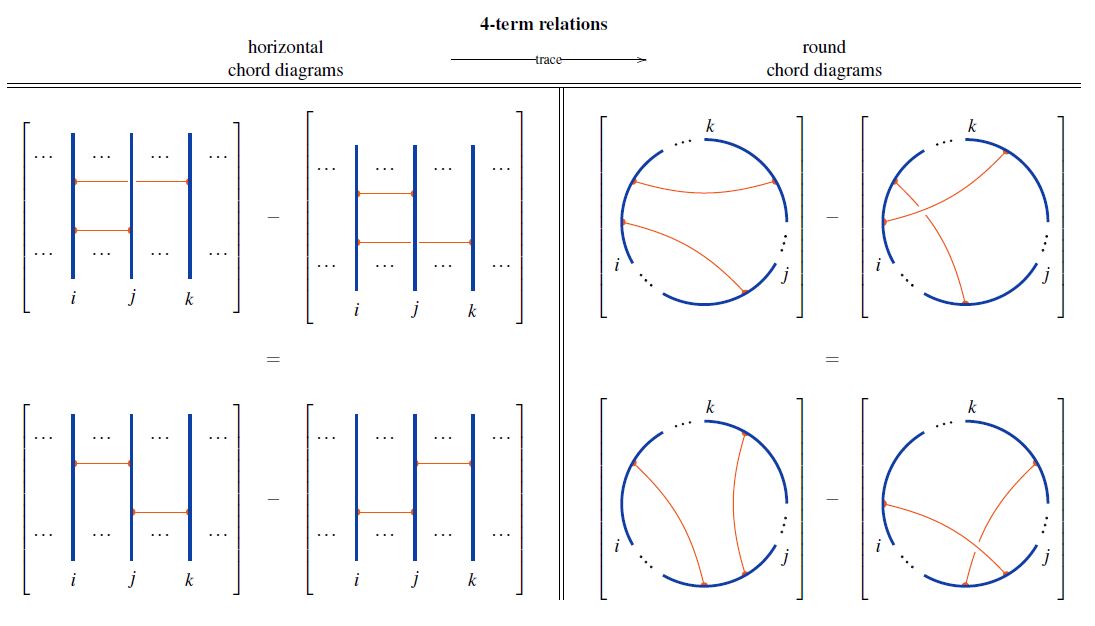
Relation between horizontal and round 4T relations
The 4T-relations for round chord diagrams are the image of the 4T relations for horizontal chord diagrams under tracing horizontal to round chord diagrams:
Relation to STU-relations
Under the embedding of the set of round chord diagrams into the set of Jacobi diagrams, the STU-relations imply the 4T relations on round chord diagrams:
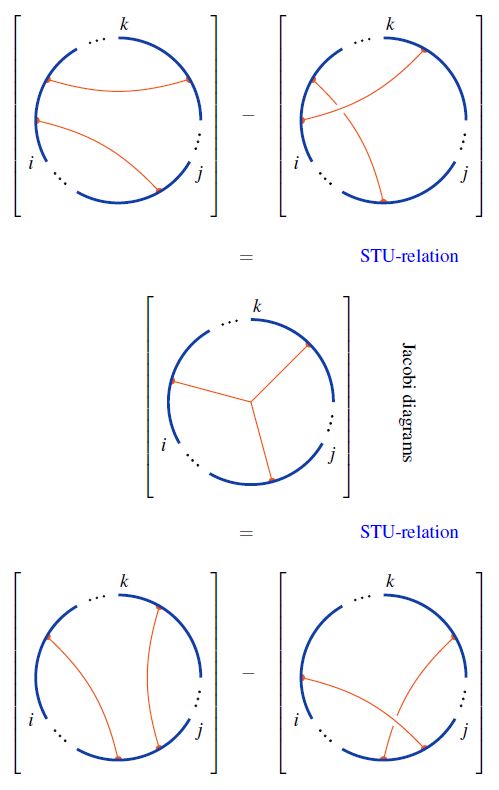
Using this, one finds that chord diagrams modulo 4T are Jacobi diagrams modulo STU:
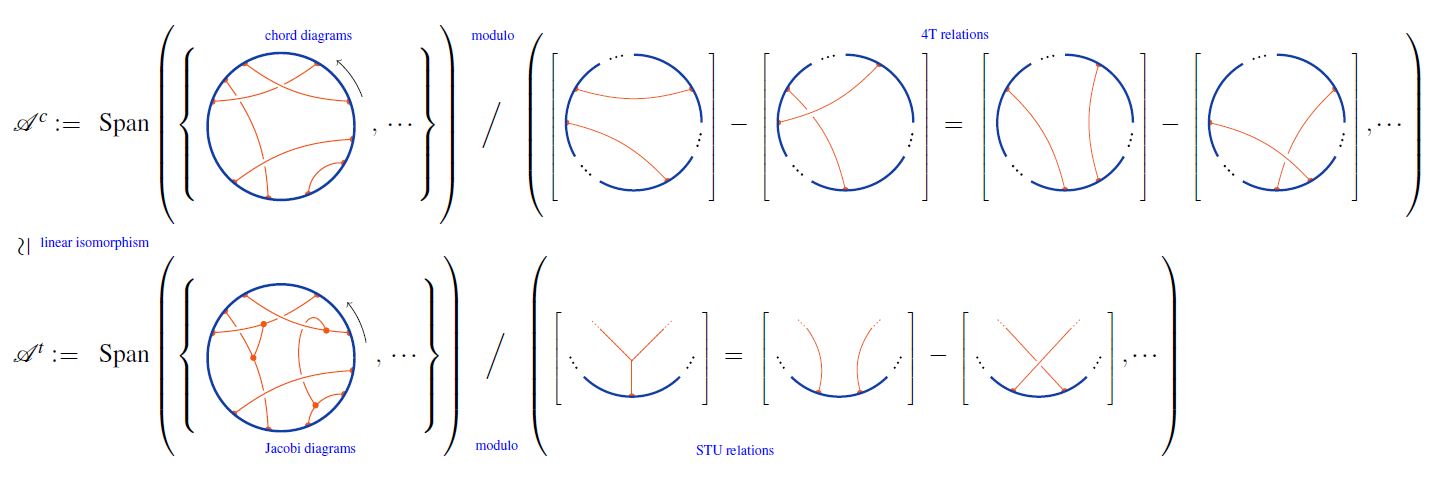
graphics from Sati-Schreiber 19c
Related concepts
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
References
Original articles
-
Dror Bar-Natan, On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)
-
Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)
Textbook accounts
-
Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 4 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv/1103.5628, doi:10.1017/CBO9781139107846)
-
David Jackson, Iain Moffat, Section 11 of: An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)
Lecture notes:
- Dror Bar-Natan, Alexander Stoimenow, The Fundamental Theorem of Vassiliev Invariants (arXiv:q-alg/9702009)
The graphics above are taken from Sati-Schreiber 19.
Last revised on December 20, 2019 at 19:34:05. See the history of this page for a list of all contributions to it.