nLab infinitesimal braid relation
Context
Knot theory
Examples/classes:
Types
Related concepts:
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Contents
Definition
Definition
(infinitesimal braid Lie algebra)
For natural numbers, let be the free Lie algebra (over a given ground field) on generators in degree with two indices ranging from 1 to and distinct.
The infinitesimal braid relations in dimension are the following relations on the underlying vector space of the free Lie algebra on generators
This defines a quotient Lie algebra often denoted
More generally, there is a version of this in any dimension with some extra signs thrown in.
This is originally due to Kohno 87 (1.1.4), it appears also in Kohno 88, Bar-Natan 96, Fact 3, Fadell-Husseini 01, Cohen-Gitler 01, Section 3.
Authors have used different equivalent versions of this presentation, see Cohen-Gitler 02, p. 2 for a clear statement.
Properties
Relation to horizontal chord diagrams
If is identified with the commutator Lie algebra of horizontal chord diagrams on strands, generated by

and forming an associative algebra under concatenation of diagrams along strands, as in
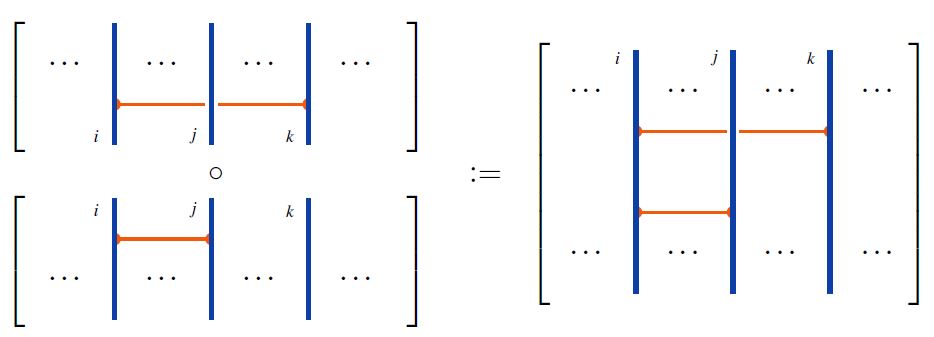
then the remaining infinitesimal braid relations (1) are equivalently the following:
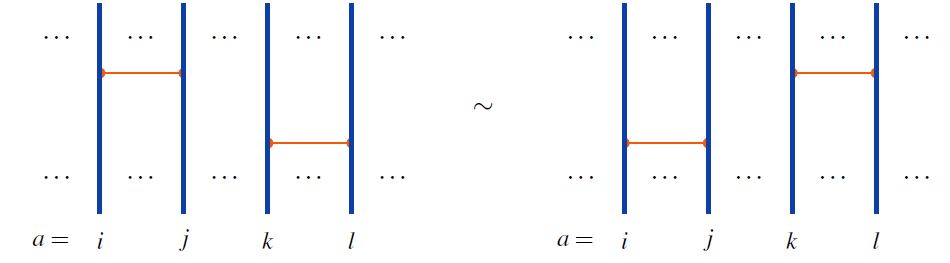
R1 is the the 2T relation:
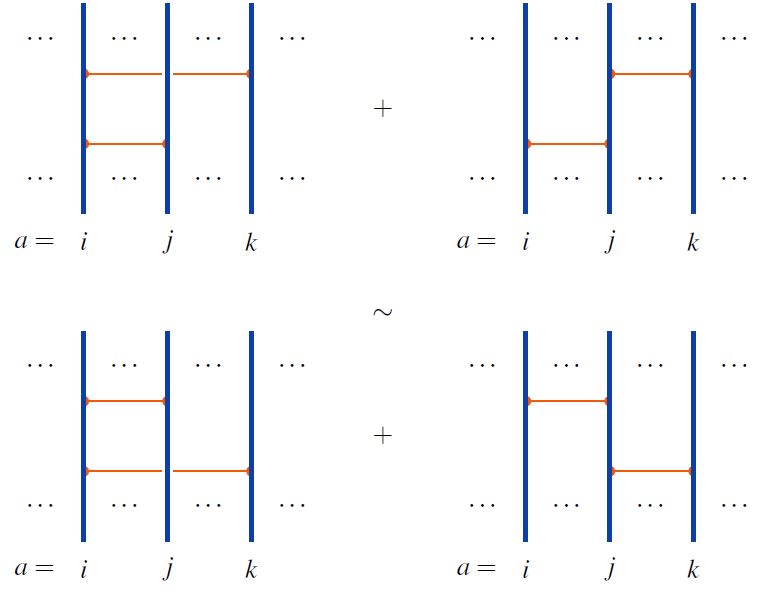
R2 is the 4T relation:
graphics from Sati-Schreiber 19c
Hence:
Proposition
(universal enveloping algebra of infinitesimal braid Lie algebra is horizontal chord diagrams modulo 2T&4T)
of horizontal chord diagrams on strands with product given by concatenation of strands (this Def.), modulo the 2T relations and 4T relations (this Def.) is isomorphic to the universal enveloping algebra of the infinitesimal braid Lie algebra (Def. ):
Related concepts
| chord diagrams | weight systems |
|---|---|
| linear chord diagrams, round chord diagrams Jacobi diagrams, Sullivan chord diagrams | Lie algebra weight systems, stringy weight system, Rozansky-Witten weight systems |
References
-
Toshitake Kohno, (1.1.4) in: Monodromy representations of braid groups and Yang-Baxter equations, Annales de l’Institut Fourier, Volume 37 (1987) no. 4, p. 139-160 (doi:10.5802/aif.1114)
-
Toshitake Kohno: Linear representations of braid groups and classical Yang-Baxter equations, in: Joan S. Birman, Anatoly Libgober (eds.) Braids, Cont. Math. 78 (1988) 339-363 [doi:10.1090/conm/078]
(in relation to the classical Yang-Baxter equation)
-
Dror Bar-Natan, Fact 3 in: Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 [arxiv:q-alg/9607001]
-
Edward Fadell, Sufian Husseini, Theorem 2.2 in: Geometry and topology of configuration spaces, Springer Monographs in Mathematics (2001) [ MR2002k:55038]
-
Fred Cohen, Samuel Gitler, Section 3 in: Loop spaces of configuration spaces, braid-like groups, and knots, In: Jaume Aguadé, Carles Broto, Carles Casacuberta (eds.) Cohomological Methods in Homotopy Theory. Progress in Mathematics, vol 196. Birkhäuser, Basel 2001 (doi:10.1007/978-3-0348-8312-2_7)
-
Fred Cohen, Samuel Gitler, p. 2 of: On loop spaces of configuration spaces, Trans. Amer. Math. Soc. 354 (2002), no. 5, 1705–1748, (jstor:2693715, MR2002m:55020)
Last revised on February 12, 2025 at 08:27:43. See the history of this page for a list of all contributions to it.