nLab Roger Penrose

Roger Penrose is a mathematical physicist at University of Oxford. He received one half of the 2020 Nobel Prize in Physics “for the discovery that black hole formation is a robust prediction of the general theory of relativity”. The other half was awarded to Reinhard Genzel and Andrea Ghez.

• Wikipedia entry

He made fundamental contributions to the study of mathematical general relativity, such as the Penrose-Hawking theorem and the discovery of the twistor space description of spacetime geometry.

Selected writings

On Penrose graphical notation (string diagrams) for tensor-calculus:

• Roger Penrose, Applications of negative dimensional tensors, Combinatorial Mathematics and its Applications, Academic Press (1971) (pdf, pdf)

• Roger Penrose, Angular momentum: An approach to combinatorial spacetime, in Ted Bastin (ed.) Quantum Theory and Beyond, Cambridge University Press (1971), pp.151-180 (pdf)

• Roger Penrose, On the nature of quantum geometry, in: J. Klauder (ed.) Magic Without Magic, Freeman, San Francisco, 1972, pp. 333–354 (spire:74082, pdf)

• Roger Penrose, Wolfgang Rindler, appendix (p. 424-434) of: Spinors and space-time – Volume 1: Two-spinor calculus and relativistic fields, Cambridge University Press 1984 (doi:10.1017/CBO9780511564048)

Introducing what came to be called the Penrose limit for obtaining pp-wave spacetimes:

• Roger Penrose, Any Space-Time has a Plane Wave as a Limit, in Differential Geometry and Relativity, Mathematical Physics and Applied Mathematics 3, Springer (1976) 271–275 [doi:10.1007/978-94-010-1508-0_23, pdf]

On spacetime in the theory of gravity/general relativity:

• Stephen Hawking, Roger Penrose, The Nature of Space and Time, Princeton University Press (1996) [ISBN 0-691-03791-4, arXiv:hep-th/9409195, Wikipedia entry]

Further selected thoughts

Mind-Maths-Matter

Penrose has highlighted the subtle philosophical issue of the
apparent interrelation of mathematics, physics and the mind (Penrose 94, section 8.7, Penrose 05):

$$\array{ && logic \\ & \swarrow && \nwarrow \\ physics &&\longrightarrow && mind }$$

Here the composite arrow from mind over logic/mathematics to nature/physics resonates with the absolute idealism of the Science of Logic.

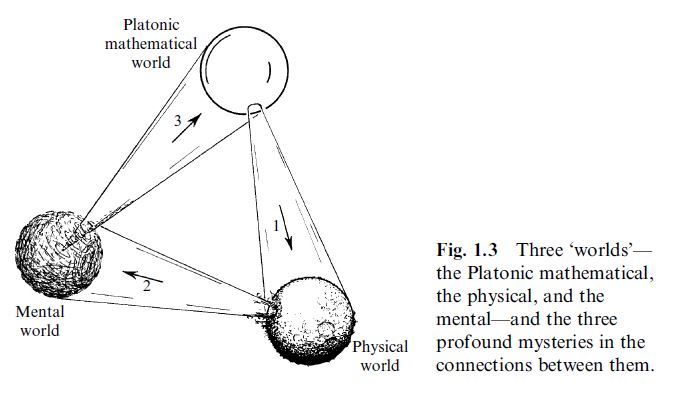
graphics grabbed from Penrose 05, Fig 1.3

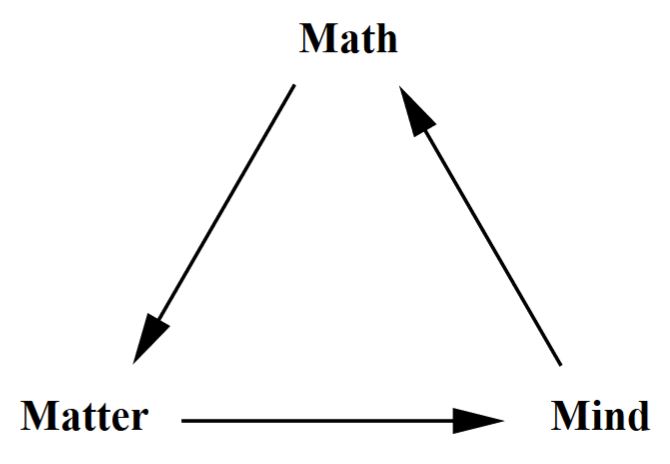
graphics grabbed from Hut-Alford-Tegmark 06

Quantum gravity effects in neurons

Penrose (controversially) argued that quantum gravity effects on decoherence of quantum superposition causes physics to be non-computable and serves to explain aspects of the human mind such as consciousness, by causing wave function collapse in microtubuli inside neurons. This latter aspect he is more recently developing in more concrete detail in quantum biology (see there for more) with Stuart Hameroff.

Moduli stabilization

In Penrose 03, section 10.3 it is pointed out that the Penrose-Hawking theorem immediately implies that in pure Einstein gravity (general relativity) small compact dimensions of spacetime, as assumed in Kaluza-Klein compactification, cannot be stable. From this the author draws the conclusion that moduli stabilization in KK-compactifications in general and in string phenomenology in particular can never work, a claim later repeated in Penrose 16.

However, all claims of moduli stabilization in the literature concern not pure gravity, but gravity coupled to a gauge field (Einstein-Maxwell theory) or higher gauge field (supergravity) with non-trivial field strength on the compact dimensions, whence called flux compactifications. It is the repulsive force of the gauge field in the compact fibers which counteracts the gravitational collapse.

This is not specific to string theory and can be seen in elementary terms (Freund-Rubin 80) and in simple toy examples such as in plain 6-dimensional Einstein-Maxwell theory (Salam et. al., 83).

Selected writings

• Roger Penrose, Shadows of the mind, Oxford University Press, New York, 1994 (Wikipedia entry)

• Roger Penrose, On the stability of extra space dimensions in Gibbons, Shellard, Rankin (eds.) The Future of Theoretical Physics and Cosmology, Cambridge (2003) (spire)

• Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Knopf 2005 (Wikipedia entry)

• Roger Penrose, Fashion, Faith, and Fantasy in the New Physics of the Universe, Princeton University Press 2016 (PP:10664)

Related $n$Lab entries

• Penrose notation

• Penrose diagram

• Penrose-Hawking theorem

• twistor space

• mind

category: people