nLab string theory

Idea

String theory is a theory in fundamental physics. Certainly it is, mathematically, a structure that contains in various limits a plethora of quantum field theories. Its interest for experimental high energy physics lies in the hypothesis that it provides a theory of everything in the sense of fundamental physics, but the jury on that is still out.

Below we indicate the basic idea and provide pointers to further details. See also the string theory FAQ.

Conceptually: From QFT worldline formalism

Perturbative string theory is something at least close to a categorification of the following description of perturbative quantum field theory in terms of sums over Feynman diagrams.

Recall that in quantum field theory one approach to make sense of the path integral is the perturbation series expansion, which interprets the path integral for the scattering amplitudes (the S-matrix) as a certain sum over graphs of certain numbers assigned to each graph.

The graphs are called Feynman diagrams, the numbers assigned to them are called (renormalized) scattering amplitudes and the sum over graphs of (renormalized) amplitudes is the perturbation series or S-matrix.

The amplitude assigned to a single graph with $n$ external edges is interpreted as the amplitude for $n$ “quanta” or “particles” of the fields in question to interact in the way indicated by the graph.

Crucial for the motivation of the idea of string theory is the observation that this (renormalized) amplitude assigned to a graph is itself the correlator of a 1-dimensional quantum field theory on that graph: the “worldline quantum field theory” describing the (relativistic) quantum mechanics of these particles. This is usually a sigma-model with parameter space the given graph and target space the spacetime on which the fields live for which the perturbation series computes the path integral.

When made explicit this is called the worldline formalism for computing the quantum field perturbation series. (See there for more details.)

The premise of perturbative string theory is to replace the perturbation series over correlators of a 1-d QFT over graphs by a sum of correlators of a 2-dQFT over 2-dimensional surfaces – called worldsheets and hence produce an S-matrix this way. Again in simple cases this 2d QFT is a sigma-model whose target is the spacetime in which one computes interactions.

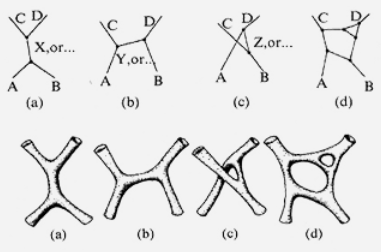
graphics grabbed from Jurke 10

In analogy to the previous case, one thinks of the amplitude assigned this way to a surface as the amplitude for the boundary arcs – the strings – to interact in the way given by the surface.

Some of the motivations for considering this replacement of graphs by surfaces have been the following:

• the 2-d correlators are better behaved in that they don’t have to be renormalized. The “counterterms” appearing in renormalization of ordinary QFT can be identified with contributions to the correlators that come from the linear extension of the strings (see the above reference for more on this);

• there are fewer choices involved: a Feynman graph is really a decorated graph with the decoration from some more or less arbitrary index set, describing the nature of the particles associated with a given edge and the nature of the interaction associated with a given vertex. In the sum over surfaces there is no extra decoration (except on the boundary of the surfaces) and one finds that instead a single string diagram (a 2d QFT correlator for a given surface) encodes already a sum over (infinitely) many particle species decorations and all possible interaction decorations for them;

• while there are fewer choices to be made by hand, it turns out that the effective particle content that does arise automatically from this prescription happens to be structurally of the kind one would hope for: the massless effective particles described by the string perturbation series happen to be gauge bosons, fermions charged under them, and, notably, gravitons. This is structurally exactly the Yang-Mills theory input of the standard model of particle physics combined with perturbative quantum gravity that one would hope to see.

These aspects have motivated the impression that the string perturbation series might be considerably closer to the true formalism of fundamental physics than ordinary perturbative quantum field theory. This impression is however offset by the following problems:

• while the worldsheet 2d QFT whose correlators are summed over surfaces are themselves much easier to handle than the full target space quantum physics they are used to encode, a fully complete and rigorous theory of 2d QFT is available only in simple special cases.

• In particular, even though there are fewer arbitrary choices involved in the string perturbation series as compared to the ordinary Feynman perturbation series, one crucial choice still present is that of this worldsheet 2d QFT. By the above, every choice of worldsheet QFT (called a choice of “vacuum”) corresponds to a choice of effective target space geometry (to be thought of as the one that the perturbation series computes the quantum perturbations about) and particle content (see 2-spectral triple for more on that). One would therefore like to understand the space of all worldsheet QFTs whose effective target space geometry and particle content is close to the one experimentally observed. After many years of rather naïve approaches to handle or not to handle this, it has more recently at least come to the general attention that there is something to be better understood here.

• More fundamentally, already the role of the original perturbation series in quantum field theory is actually not fully understood. Its main success is the observation that truncating or resumming the perturbation series in a more or less ad hoc way, it does yield values that very well describe a plethora of real world measurements. One imagines that there is a non-perturbative definition of quantum field theory such that in certain well-defined circumstances the perturbation series does yield an approximation to it and is a posteriori justified. If so, there should be an analogous nonperturbative definition of string theory. There is a large ratio of speculations as to what that might be over solid results about it.

Phenomenologically

While therefore the premise of perturbative string theory is conceptually suggestive for various reasons, there is to date no connection to experimental phenomenology (apart from the fact that conceptual insights into string theory have helped analyze quantum field theoretic data, see at string theory results applied elsewhere). As a result much of the substantial outcome of string theory research is more in mathematical physics (if done well, at least), exploring the general theory space of quantum field theories and their UV-completions, than in realistic model building (though there is no lack of trying), where it remains very speculative. This has led to public or semi-public debates about the value of string theory for actual physics. See at criticism of string theory for pointers.

Scales and (no) parameters

• string tension$T = 1/(2\pi \alpha^\prime)$

• string length scale$l_s = \sqrt{\alpha'}$

• string coupling constant$g_s = e^\lambda$

  (= radius of M-theory compactification circle (Witten 95))

• coupling constant of gravity: $\kappa \propto g_s (\alpha')^6 = g_s l_s^{12}$

• Newton's constant (before compactification) $G_N = \kappa^2/8\pi$

• Planck length$l_P = (8 \pi G_N)^{1/24} = \kappa^{1/12} \propto l_s g_s^{1/12}$

• Planck mass$M_p = l_p^{-1}$

(see e.g. arXiv:0908.0333)

see also at non-perturbative effect the section Worldsheet and brane instantons and at fundamental scales – contents

Critical string theories and quantum anomalies

The action functional for the string-sigma model in general has a quantum anomaly of both kinds:

1. For both the bosonic string and the superstring the corresponding Polyakov action has a gauge anomaly for the conformal symmetry, depending on the dimension $d$ of target space, and on the strength of the dilaton background field. For vanishing dilaton field this anomaly vanishes exactly for $d = 26$ for the bosonic model, and in $d = 10$ for the superstring.

   For target spaces of these dimensions one speaks of critical string theory. In as far as string theory is expected to have relevance for physics at all, it is usually expected to be in this critical dimension. But also noncritical string models can and have been considered.

2. Apart from the gauge anomaly, the action functional of the string-sigma-model also in general has an anomalous action functional , for two reasons:

   1. The higher holonomy of the higher background gauge fields is in general not a function, but a section of a line bundle;

   2. The fermionic path integral over the worldsheet-spinors of the superstring produces as section of a Pfaffian line bundle.

   In order for the action functional to be well-defined, the tensor product of these different anomaly line bundles over the bosonic configuration space must have trivial class (as bundles with connection, even). This gives rise to various further anomaly cancellation conditions:

   1. For the heterotic string (necessarily closed) the anomaly cancellation condition is known as the Green-Schwarz mechanism : it says that the background fields of gravity and B-field must organize to a twisted differential string structure whose twist is given by the background Yang-Mills field.

   2. For the open type II string the condition is known as the Freed-Witten anomaly cancellation condition: it says that the restriction of the B-field to any D-brane must consistute the twist of a twisted spin^c structure on the brane.

      A more detailed analysis of these type II anomalies is in (DFMI) and (DFMII).

      See also Diaconescu-Moore-Witten anomaly.

Subtopics

Ingredients

• quantum field theory

• sigma-model,

  • 2d CFT, 2d SCFT, 2-spectral triple

    • Dirac-Ramond operator

    • Witten genus

    • Gepner model, flop transition

  • world sheets for world sheets

• Goddard-Thorn no-ghost theorem, GSO projection

• perturbation theory

  • string scattering amplitude, S-matrix

• effective background QFT

  • gravity, supergravity, Yang-Mills theory, quantum gravity

  • quantum anomaly

  • twisted smooth cohomology in string theory

Critical string models

• heterotic string theory

  • Green-Schwarz mechanism, differential string structure,

  • dual heterotic string theory

    • differential fivebrane structure

  • Witten genus, string orientation of tmf

• type II string theory

  • type II geometry

  • elliptic genus

  • Diaconescu-Moore-Witten anomaly

• type I string theory

• type 0 string theory

• little string theory

• Kaluza-Klein mechanism

  • double dimensional reduction

  • moduli stabilization

  • flux compactification

  • landscape of string theory vacua

• string field theory

• duality in string theory

  • T-duality, mirror symmetry

  • S-duality, electric-magnetic duality

  • U-duality

  • open/closed string duality

    • AdS/CFT, holographic principle

    • KLT relations

• 11-dimensional supergravity, M-theory

  • Hořava-Witten theory

Extended objects

• brane

• D-brane

  • D0-brane, D2-brane, D4-brane

  • D1-brane, D3-brane, D5-brane

  • RR-field, differential K-theory

• black brane

  • black holes in string theory

• NS-brane

  • string, sigma-model

    • spinning string, superstring

    • B2-field

  • NS5-brane

    • B6-field

• M-brane

  • M2-brane

    • C3-field

    • ABJM theory, BLG model

  • M5-brane

    • C6-field

    • 6d (2,0)-supersymmetric QFT

Table of branes appearing in supergravity/string theory (for classification see at brane scan).

brane	in supergravity	charged under gauge field	has worldvolume theory
black brane	supergravity	higher gauge field	SCFT
D-brane	type II	RR-field	super Yang-Mills theory
$(D = 2n)$	type IIA	$\,$	$\,$
D(-2)-brane	$\,$	$\,$
D0-brane	$\,$	$\,$	BFSS matrix model
D2-brane	$\,$	$\,$	$\,$
D4-brane	$\,$	$\,$	D=5 super Yang-Mills theory with Khovanov homology observables
D6-brane	$\,$	$\,$	D=7 super Yang-Mills theory
D8-brane	$\,$	$\,$
$(D = 2n+1)$	type IIB	$\,$	$\,$
D(-1)-brane	$\,$	$\,$	$\,$
D1-brane	$\,$	$\,$	2d CFT with BH entropy
D3-brane	$\,$	$\,$	N=4 D=4 super Yang-Mills theory
D5-brane	$\,$	$\,$	$\,$
D7-brane	$\,$	$\,$	$\,$
D9-brane	$\,$	$\,$	$\,$
(p,q)-string	$\,$	$\,$	$\,$
(D25-brane)	(bosonic string theory)
NS-brane	type I, II, heterotic	circle n-connection	$\,$
string	$\,$	B2-field	2d SCFT
NS5-brane	$\,$	B6-field	little string theory
D-brane for topological string			$\,$
A-brane			$\,$
B-brane			$\,$
M-brane	11D SuGra/M-theory	circle n-connection	$\,$
M2-brane	$\,$	C3-field	ABJM theory, BLG model
M5-brane	$\,$	C6-field	6d (2,0)-superconformal QFT
M9-brane/O9-plane			heterotic string theory
M-wave
topological M2-brane	topological M-theory	C3-field on G2-manifold
topological M5-brane	$\,$	C6-field on G2-manifold
S-brane
SM2-brane, membrane instanton
M5-brane instanton
D3-brane instanton
solitons on M5-brane	6d (2,0)-superconformal QFT
self-dual string		self-dual B-field
3-brane in 6d

Scattering amplitudes

• S-matrix

• Veneziano amplitude

• string scattering amplitude

• p-adic string theory

Elliptic genera, elliptic cohomology and $tmf$

A properly developed theory of elliptic cohomology is likely to shed some light on what string theory really means. (Witten 87, very last sentence)

The large volume limit of the partition function of the superstring on a given target spacetime is an elliptic genus of that manifold (Witten 87), the Witten genus (see there for more).

Since the Witten genus in turn is the decategorification of the string orientation of tmf, this suggests that tmf-generalized (Eilenberg-Steenrod) cohomology classifies full string theories, in refinement of how the classification of D-brane charge (just the boundary conditions for open strings) is given by K-theory.

A non-trivial conistency check of this idea is announced in (Nikolaus 14).

Topological strings

• A-model, B-model

String phenomenology

• string phenomenology

  • G2-MSSM

String theory results applied elsewhere

Beyond the speculative hypothetized role of string theory as a theory behind observed particle physics, the theory has shed light on many aspects of quantum field theory, both on the conceptual structure of quantum field theory as such as well as on concrete theories and their concrete properties. Some of these string theory results enter crucially in computations that are used to interpret particle physics experiments such as the LHC.

For more see

• string theory results applied elsewhere

References

General

Popular exposition:

• Michael Green, Superstrings, Scientific American Vol. 255, No. 3 (September 1986), pp. 48-63 (jstor:24976036)

Textbooks on string theory and M-theory include the following (for more see at books about string theory):

• Mike Duff

  The World in Eleven Dimensions: Supergravity, Supermembranes and $M$-theory,

  IoP 1999 (publisher)

• Joseph Polchinski, String theory, Cambridge Monographs on Mathematical Physics (2001)

• Pierre Deligne, Pavel Etingof, Dan Freed, L. Jeffrey, David Kazhdan, John Morgan, D.R. Morrison and Edward Witten, eds.

  Quantum Fields and Strings, A course for mathematicians, 2 vols. Amer. Math. Soc. Providence 1999. (web version)

• Michael Douglas, Elias Kiritsis et. al. (eds.),

  String theory and the real world,

  Les Houches Session LXXXVII 2007

• Ralph Blumenhagen, Dieter Lüst, Stefan Theisen,

  Basic Concepts of String Theory,

  Springer (2013) [doi:10.1007/978-3-642-29497-6]

• Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory ,Proceedings of Symposia in Pure Mathematics, volume 83 AMS (2011)

• Luis Ibáñez, Angel Uranga,

  String Theory and Particle Physics – An Introduction to String Phenomenology,

  Cambridge University Press 2012

• Peter West,

  Introduction to Strings and Branes,

  Cambridge University Press 2012

• Gregory Moore,

  The Impact of D-Branes on Mathematics,

  talk at PolchinskiFest 2014 (pdf)

• Gregory Moore,

  Physical Mathematics and the Future

  talk at Strings 2014 (talk slides, companion text pdf, pdf)

• Gordon Kane,

  String theory and the real world,

  Morgan & Claypool, 2017 (doi:0.1088/978-1-6817-4489-6)

  (on M-theory on G2-manifolds and the G2-MSSM)

• Mikio Nakahara,

  Chapter 14 of: Geometry, Topology and Physics,

  IOP 2003

  (doi:10.1201/9781315275826, pdf)

Lecture notes:

• Satoshi Nawata, Runkai Tao, Daisuke Yokoyama, Fudan lectures on string theory [arXiv:2208.05179]

A large body of references is organized at the

• String Theory Wiki

A quick survey of the big picture as of 2016 is in

• Ashoke Sen, What is string theory?, talk at YITP50, Stony Brook 2016 (pdf)

Survey of the status of string theory as a theory of quantum gravity:

• Matthias Blau, String theory as a theory of quantum gravity – A status report Talk at Quantum theory and Gravitation Zürich (2011) (pdf)

Annual conference

• Strings 2022

An article summarizing information about cohomological models for aspects of string theory and listing plenty of useful further references is

• Hisham Sati, Geometric and topological structures related to M-branes

Polyakov gauge/string duality

Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see notably also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical remarks in Polyakov (2008)) under the name gauge/string duality (cf. historical review in Polyakov (2008)), in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings:

Early suggestion that confined QCD is described by regarding the color-flux tubes as string-like dynamical degrees of freedoms:

• John Kogut, Leonard Susskind, Vacuum polarization and the absence of free quarks in four dimensions, Phys. Rev. D 9 (1974) 3501-3512 $[$doi:10.1103/PhysRevD.9.3501$]$

• Kenneth G. Wilson, Confinement of quarks, Phys. Rev. D 10 (1974) 2445 $[$doi:10.1103/PhysRevD.10.2445$]$

  (argument in lattice gauge theory)

• John Kogut, Leonard Susskind, Hamiltonian formulation of Wilson’s lattice gauge theories, Phys. Rev. D 11 (1975) 395 $[$doi:10.1103/PhysRevD.11.395$]$

  “The gauge-invariant configuration space consists of a collection of strings with quarks at their ends. The strings are lines of non-Abelian electric flux. In the strong coupling limit the dynamics is best described in terms of these strings. Quark confinement is a result of the inability to break a string without producing a pair. $[$…$]$”

  “The confining mechanism is the appearance of one dimensional electric flux tubes which must link separated quarks. The appropriate description of the strongly coupled limit consists of a theory of interacting, propagating strings. $[$…$]$”

  “This picture of the strongly coupled Yang-Mills theory in terms of a collection of stringlike flux lines is the central result of our analysis. It should be compared with the phenomenological use of stringlike degrees of freedom which has been widely used in describing hadrons.”

• Alexander Polyakov, String representations and hidden symmetries for gauge fields, Physics Letters B 82 2 (1979) 247-250 $[$doi:10.1016/0370-2693(79)90747-0$]$

• Alexander Polyakov, Gauge fields as rings of glue, Nuclear Physics B 164 (1980) 171-188 $[$doi:10.1016/0550-3213(80)90507-6$]$

  “The basic idea is that gauge fields can be considered as chiral fields, defined on the space of all possible contours (the loop space). The origin of the idea lies in the expectation that, in the confining phase of a gauge theory, closed strings should play the role of elementary excitations.”

• Yuri Makeenko, Alexander A. Migdal, Quantum chromodynamics as dynamics of loops, Nuclear Physics B 188 2 (1981) 269-316 $[$doi:10.1016/0550-3213(81)90258-3$]$

  “So the world sheet of string should be interpreted as the color magnetic dipole sheet. The string itself should be interpreted as the electric flux tube in the monopole plasma.”

• Alexander Polyakov, Gauge Fields and Strings, Routledge, Taylor and Francis (1987, 2021) $[$doi:10.1201/9780203755082, oapen:20.500.12657/50871$]$

$[$old personal page$]$: “My main interests this year $[$1993?$]$ were directed towards string theory of quark confinement. The problem is to find the string Lagrangian for the Faraday’s ”lines of force“,which would reproduce perturbative corrections from the Yang-Mills theory to the Coulomb law at small distances and would give permanent confinement of quarks at large distances.”

Early suggestion, due to the Liouville field seen in the quantization of the bosonic string via the Polyakov action,

• Alexander Polyakov, Quantum geometry of bosonic strings, Phys. Lett. B 103 (1981) 207-210 $[$doi:10.1016/0370-2693(81)90743-7, pdf$]$

that such flux tubes regarded as confining strings are to be thought of a probing higher dimensional spacetime, exhibiting a holographic principle in which actual spacetime appears as a brane:

• Alexander Polyakov, String Theory and Quark Confinement, talk at Strings’97, Nucl. Phys. Proc. Suppl. 68 (1998) 1-8 $[$arXiv:hep-th/9711002, doi:10.1016/S0920-5632(98)00135-2$]$

  “In other words the open string flies in the $(x,\phi)$-space keeping its feet (its ends) on the ground $(\phi=0)$.”

• Alexander Polyakov, The wall of the cave, Int. J. Mod. Phys. A 14 (1999) 645-658 $[$arXiv:hep-th/9809057, doi:10.1142/S0217751X99000324$]$

  “We add new arguments that the Yang-Mills theories must be described by the non-critical strings in the five dimensional curved space. The physical meaning of the fifth dimension is that of the renormalization scale represented by the Liouville field.”

eventually culminating in the formulation of the dictionary for the AdS-CFT correspondence:

• Steven Gubser, Igor Klebanov, Alexander Polyakov, Gauge theory correlators from non-critical string theory, Physics Letters B 428 105-114 (1998) $[$hep-th/9802109, doi:10.1016/S0370-2693(98)00377-3$]$

“Relations between gauge fields and strings present an old, fascinating and unanswered question. The full answer to this question is of great importance for theoretical physics. It will provide us with a theory of quark confinement by explaining the dynamics of color-electric fluxes.”

• Alexander Polyakov, Vyacheslav Rychkov Gauge fields-strings duality and the loop equation, Nucl. Phys. B 581 (2000) 116-134 $[$arXiv:hep-th/0002106, doi:10.1016/S0550-3213(00)00183-8$]$

and the suggestion of finding the string-QCD correspondence:

• Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A 17 S1 (2002) 119-136 $[$arXiv:hep-th/0110196, doi:10.1142/S0217751X02013071$]$

“in the strong coupling limit of a lattice gauge theory the elementary excitations are represented by closed strings formed by the color-electric fluxes. In the presence of quarks these strings open up and end on the quarks, thus guaranteeing quark confinement. Moreover, in the $SU(N)$ gauge theory the strings interaction is weak at large $N$. This fact makes it reasonable to expect that also in the physically interesting continuous limit (not accessible by the strong coupling approximation) the best description of the theory should involve the flux lines (strings) and not fields, thus returning us from Maxwell to Faraday. In other words it is natural to expect an exact duality between gauge fields and strings. The challenge is to build a precise theory on the string side of this duality.”

Historical reminiscences:

• Alexander Polyakov, Confinement and Liberation, in Gerardus ’t Hooft (ed.) 50 Years of Yang-Mills Theory (2005) 311-329 $[$arXiv:hep-th/0407209, doi:10.1142/9789812567147_0013, doi:10.1142/5601$]$

“Already in 1974, in his famous large $N$ paper, ‘t Hooft already tried to find the string-gauge connections. His idea was that the lines of Feynman’s diagrams become dense in a certain sense and could be described as a 2d surface. This is, however, very different from the picture of strings as flux lines. Interestingly, even now people often don’t distinguish between these approaches. In fact, for the usual amplitudes Feynman’s diagrams don’t become dense and the flux lines picture is an appropriate one. However there are cases in which t’Hooft’s mechanism is really working.”

• Alexander M. Polyakov, §1 in: Beyond Space-Time, in The Quantum Structure of Space and Time, Proceedings of the 23rd Solvay Conference on Physics, World Scientific (2007) $[$arXiv:hep-th/0602011, pdf$]$

• Alexander M. Polyakov, From Quarks to Strings $[$arXiv:0812.0183$]$

  published as Quarks, strings and beyond, section 44 in: Paolo Di Vecchia et al. (ed.), The Birth of String Theory, Cambridge University Press (2012) 544-551 $[$doi:10.1017/CBO9780511977725.048$]$

  “By the end of ’77 it was clear to me that I needed a new strategy $[$for understanding confinement$]$ and I became convinced that the way to go was the gauge/string duality. $[$…$]$”

  “Classically the string is infinitely thin and has only transverse oscillations. But when I quantized it there was a surprise – an extra, longitudinal mode, which appears due to the quantum ”thickening“ of the string. This new field is called the Liouville mode. $[$…$]$”

  “I kept thinking about gauge/strings dualities. Soon after the Liouville mode was discovered it became clear to many people including myself that its natural interpretation is that random surfaces in 4d are described by the strings flying in 5d with the Liouville field playing the role of the fifth dimension. The precise meaning of this statement is that the wave function of the general string state depends on the four center of mass coordinates and also on the fifth, the Liouville one. In the case of minimal models this extra dimension is related to the matrix eigenvalues and the resulting space is flat.”

  “Since this 5d space must contain the flat 4d subspace in which the gauge theory resides, the natural ansatz for the metric is just the Friedman universe with a certain warp factor. This factor must be determined from the conditions of conformal symmetry on the world sheet. Its dependence on the Liouville mode must be related to the renormalization group flow. As a result we arrive at a fascinating picture – our 4d world is a projection of a more fundamental 5d string theory. $[$…$]$”

  “At this point I was certain that I have found the right language for the gauge/string duality. I attended various conferences, telling people that it is possible to describe gauge theories by solving Einstein-like equations (coming from the conformal symmetry on the world sheet) in five dimensions. The impact of my talks was close to zero. That was not unusual and didn’t bother me much. What really caused me to delay the publication (Polyakov 1998) for a couple of years was my inability to derive the asymptotic freedom from my equations. At this point I should have noticed the paper of Klebanov 1997 in which he related D3 branes described by the supersymmetric Yang Mills theory to the same object described by supergravity. Unfortunately I wrongly thought that the paper is related to matrix theory and I was skeptical about this subject. As a result I have missed this paper which would provide me with a nice special case of my program. This special case was presented little later in full generality by Juan Maldacena (Maldacena 1997) and his work opened the flood gates.”

Higher structures

Discussion from the nPOV/Higher Structures:

• Branislav Jurco, Christian Saemann, Urs Schreiber, Martin Wolf,

  Higher Structures in M-Theory,

  Introduction to Higher Structures in M-Theory, LMS-EPSRC Durham Symposium, August 2018, Fortsch. d. Phys. 2019 (arXiv:1903.02807)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber,

  The rational higher structure of M-theory

  in Proceedings of the LMS-EPSRC Durham SymposiumHigher Structures in M-Theory, August 2018, Fortschritte der Physik, 2019 (arXiv:1903.02834)

• Urs Schreiber,

  Introduction to Higher Supergeometry

  Lectures at Higher Structures in M-Theory, LMS-EPSRC Durham Symposium, August 2018

More technical details

GUT

A key article for the idea that string theory provides a framework for realistic (chiral) grand unified theories combined with quantum gravity was

• Edward Witten, Some properties of $O(32)$ superstrings, Phys. Lett. B, volume 149, December 1984 (pdf)

based on the insights of Green-Schwarz anomaly cancellation.

Elliptic genera, elliptic homology and tmf

The partition function of the superstring was understood to be an elliptic genus (the Witten genus) in

• Edward Witten, Elliptic Genera And Quantum Field Theory , Commun.Math.Phys. 109 525 (1987) (Euclid)

A nontrivial consistency check on the suggestion that this means that string backgrounds are classified in tmf is given in

• Thomas Nikolaus, T-Duality in K-theory and Elliptic Cohomology, talk at String Geometry Network Meeting, Feb 2014, ESI Vienna (website)

Quantum anomalies

Discussion of type II quantum anomalies is in

• Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv, slides)

• Jacques Distler, Dan Freed, Greg Moore, Spin structures and superstrings (arXiv:1007.4581)

Discussion of superstring perturbation theory is in

• Edward Witten, Superstring Perturbation Theory Revisited (arXiv:1209.5461)

Fields medal (and other) work related to string theory

Pure mathematics work which is closely related string theory and was awarded with a Fields medal includes the following.

Richard Borcherds, 1998

• vertex algebras

  • monster vertex algebra, Goddard-Thorn theorem

Maxim Kontsevich, 1998

• homological mirror symmetry,

• Gromov-Witten theory

• formality theorem and formal deformation quantization via holography of Poisson sigma-model string.

Edward Witten, 1990

• knot invariants via WZW model-string/Chern-Simons theory holography;

• elliptic genus, Witten genus and rigidity via superstring partition functions;

• mirror symmetry via A-model/B-model topological string)

Grigori Perelman, 2006

• Ricci flow for string sigma-model in dilaton gravity background

Maryam Mirzakhani, 2014

• The dynamics and geometry of Riemann surfaces and their moduli spaces, including a new proof of the Witten conjecture

In (Madsen 07) it says with respect to the proof (Madsen-Weiss 02) of the Mumford conjecture:

These tools $[$ used in the proof $]$ are all rather old, known for at least twenty years, and one may wonder why they have not before been put to use in connection with the Riemann moduli space. Maybe we lacked the inspiration that comes from the renewed interaction with physics, exemplified in conformal field theories.

History

• Joël Scherk, An introduction to the theory of dual models and strings, Rev. Mod. Phys. 47 123 (1975) [doi:10.1103/RevModPhys.47.123]

  (on the Nambu-Goto action for the relativistic string, then motivated as an explanation for quantum hadrodynamics, cf. Polyakov gauge-string duality)

• Murray Gell-Mann, introductory talk at Shelter Island II, 1983 (pdf)

  in: Shelter Island II: Proceedings of the 1983 Shelter Island Conference on Quantum Field Theory and the Fundamental Problems of Physics. MIT Press. pp. 301–343. ISBN 0-262-10031-2.

• Paul H. Frampton, Dual Resonance Models and Superstrings, World Scientific (1986) [doi:10.1142/0249]

• John Schwarz, The Second Superstring Revolution, Colloquium-level lecture presented at the Sakharov Conference (Moscow, May 1996), in: Proceedings of COSMION 96: 2nd International Conference on Cosmo Particle Physics Dedicated to the 75th Anniversary of Andrei D. Sakharov, Moscow (1996) [arXiv:hep-th/9607067, spire:969846]

  (on the “second superstring revolution”: the realization of D-branes, dualities in string theory and M-theory)

• Andrea Cappelli, Elena Castellani, Filippo Colomo, Paolo Di Vecchia (eds.), The Birth of String Theory, Cambridge University Press (2012) [doi:10.1017/CBO9780511977725]

• John Schwarz, The Early Years of String Theory: A Personal Perspective [arXiv:0708.1917],

  published as Gravity, unification, and the superstring, Section 3 in: Paolo Di Vecchia et al. (eds.) The birth of string theory, Cambridge University Press (2012) 37- [doi:10.1017/CBO9780511977725.005]

  (on the early history of string theory up to the “first superstring revolution”, the construction of the Green-Schwarz-anomaly-free $SO(32)$ type I string theory and heterotic string)

• Gabriele Veneziano, Rise and fall of the hadronic string, Section 2 in: Paolo Di Vecchia et al. (eds.), The Birth of String Theory (2012) [doi:10.1017/CBO9780511977725.004, lecture video:15073]

• Paolo Di Vecchia, The birth of string theory [arXiv:0704.0101]

  published as: From the S-matrix to string theory, Section 11 in: Paolo Di Vecchia et al. (eds.), The Birth of String Theory, Campridge University Press (2011) 156-178 [doi:10.1017/CBO9780511977725]

• Alexander M. Polyakov, From Quarks to Strings [arXiv:0812.0183]

  published as Quarks, strings and beyond, section 44 in: Paolo Di Vecchia et al. (ed.), The Birth of String Theory, Cambridge University Press (2012) 544-551 [doi:10.1017/CBO9780511977725.048]

  (on gauge/string duality)

• John Schwarz, String Theory in the Twentieth Century, talk at Strings 2016 (pdf, pdf)

• Hiroshi Itoyama, Birth of String Theory, Progress of Theoretical and Experimental Physics 2016 6 (2016) 06A103 [arXiv:1604.03701, doi:10.1093/ptep/ptw063]

• Lars Brink, Hadronic Strings – A Revisit in the Shade of Moonshine, J. Phys. A: Math. Theor. 53 (2020) 091001 [arxiv:1911.06026, doi:10.1088/1751-8121/ab6b93]