nLab string phenomenology
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Physics
physics, mathematical physics, philosophy of physics
Surveys, textbooks and lecture notes
theory (physics), model (physics)
experiment, measurement, computable physics
-
-
-
Axiomatizations
-
Tools
-
Structural phenomena
-
Types of quantum field thories
-
Contents
- Idea
- Top-down models and bottom-up models
- Semi-realistic models in string theory
- Models in heterotic string theory
- Models in type II string theory / F-theory
- Models in M-theory
- Non-supersymmetric models
- Related concepts
- References
Idea
String phenomenology is phenomenology in particle physics and cosmology based on models that are derived or at least motivated from string theory (as effective QFTs from string vacua).
Broadly speaking, string phenomenology refers to investigations of the connection of string theory to experimentally observed physics. More restrictively it refers to constructions of string theory vacua whose effective field theory reproduces the standard model of particle physics and/or the standard model of cosmology.
String theory models naturally match the general conceptual structure of the standard model of particle physics plus gravity (which is what drives the interest in string theory in the first place): for instance the standard model is a four dimensional QFT with a non-Abelian gauge symmetry, several families of chiral fermions and hierarchical Yukawa couplings – and the same is true for the generic compactification of the effective QFT that describes heterotic string theory on a 6-dimensional compact space (CHSW85) as well as for 11-dimensional supergravity/M-theory compactified on a G₂-manifold (AW01).
This structure alone already implies a variety of 3-body decays of the heavier fermions into the lighter ones and the existence of massive vector bosons coupling to charged currents, which in the observed standard model of particle physics are the W-boson, etc. (See section III of AKK12 for an exposition.)
Therefore it is not hard to find string theory compactifications that resemble the observed particle physics in broad strokes. Under some simplifying assumptions many string models have been built that very closely resemble also the fine-structure of the standard model.
A central technical issue with string model building is that of the Kaluza-Klein mechanism involved: the moduli stabilization. Historically there had been the hope that the consistency condition of moduli stabilization on string models is so strong that it strongly reduces the number of models that look like the standard model. Arguments that the number is still “not small” even with various extra assumptions lead to the term of a landscape (moduli space) of string theory models, which remains, however, poorly understood. Arguments for properties of low-energy effective QFTs that rule out a possible string-theoretic model have been brought forward for instance in (Vafa05). A review of what is known about the space of possibilities is in (Taylor11).
While all this remains poorly understood, a noteworthy difference of string phenomenology to model building in bare QFT is that a) there is a larger framework at all in which to search for models and b) with every model automatically comes a UV-completion, which is the basic motivation for embedding the standard model of particle physics in a broader theory of quantum gravity in the first place.
A good account of what it means to have a realistic string theory model and what the subtleties are, and in which sense they have already been found abundantly or not at all, is in the introduction of (Dolan-Krippendorf-Quevedo).
Top-down models and bottom-up models
Since a realistic string theoretic model is, by design, a unification of the standard model of particle physics with quantum gravity aspects and hence at least with aspects of the standard model of cosmology, there are more constraints on such a model than are usually imposed on model building in particle physics alone: the model is not only supposed to reproduce the fundamental particle content but also address moduli stabilization, the cosmological constant and dark matter (see e.g. Dolan-Krippendorf-Quevedo 11, p. 3).
Accordingly one strategy to build models is to first aim for the correct fundamental particle content, and then incrementally adjust to account for the global gravitational constraints. For instance in type II intersecting brane models people often consider just an open neighbourhood of a singular point in a KK-compactification space, adjust the model there, and then later ask about embedding this local construction into an actually globally defined compactification space (typically a Calabi-Yau manifold for compactifications aiming for low energy supersymmetry in the effective 4d model).
This approach is known as the bottom-up approach to string model building (AIQU 00).
Contrary to this is the historically older top-down approach (usually attributed to (Candelas-Horowitz-Strominger-Witten 85)) in the heterotic string theory compactification models (see below).
Semi-realistic models in string theory
Examples of models in string phenomenology include
See at References - Models below.
Models in heterotic string theory
The models in heterotic string theory follow the historically original and hence oldest strategy of finding semi-realistic GUT models in string theory (see (Witten 02) for a brief list of motivations for these models): one considers a Kaluza-Klein compactification of heterotic string theory/heterotic supergravity on a closed manifold of dimension 6 with a non-trivial gauge field configuration on it. By choosing different values of the holonomy of this gauge field around non-trivial singular 1-cycles in the compact space (usually referred to as “Wilson lines” in this context) one obtains different effective physics in the remaining 4-dimensional space.
Since most of string model building was aimed for reproducing the minimally supersymmetric extension of the standard model of particle physics, these approaches usually take that compact 6-manifold to be a complex 3-dimensional Calabi-Yau manifold.
In more detail, the paradigm of this approach is compactification of the E8 E8 heterotic string theory on a Calabi-Yau manifold of Euler characteristic , leading to a three-generation E6-model. Further gauge spontaneous symmetry breaking may be achieved e.g. by the addition of Wilson lines and a final breakdown of , supersymmetry is assumed to take place due to some field-theoretical non-perturbative effects.
See at References - Models in heterotic string theory
The lift of these heterotic CY3-compactifications to M-theory is M-theory on G₂-manifolds, discussed below.
Models in type II string theory / F-theory
In contrast to the construction of “heterotic standard models” above, which are basically plain variants of the old Kaluza-Klein compactification mechanism where the effective gauge fields in 4-dimensional spacetime arise as components of the field of gravity in higher dimensions, in type II string theory with D-branes there are open strings whose massless excitations yield gauge fields “directly”. The precise nature of these gauge fields and their couplings depends on the precise boundary conditions of these open strings, hence on the choice of D-branes that they end on.
Therefore in what are called “intersecting D-brane models” one considers Kaluza-Klein compactifications of type II string theory with D-branes that intersect in an intricate pattern in the compactification space. By choosing this intersection geometry suitably, one obtains various different realizations of gauge theory in the effective 4-dimensional physics.
The intersecting branes of main relevance in type IIA string theory are D6-branes (e.g. Lüst 04, Ibanez-Uranga 12, section 10), which, under T-duality, correspond in type IIB to D7-branes. These are precisely the ones whose lift to M-theory correspond to conifold/ADE orbifold singularities of KK-monopoles, see also at F-branes – table.
One way to neatly reorganize the required data for such type II compactifications is to formulate them in terms of “F-theory”, which is why some of this type II model building now goes by names like “F-theory phenomenology” or similar.
The moduli stabilization in these type of models can be achieved by choosing the various RR-field and B-field field strength (the “fluxes”) on the compactification space such that its curvature forms have certain specified periods on non-trivial singular cycles of the compactification space. See (Denef 08) for introduction and review of such type IIB flux compactification.
Since there are only finitely many – but many – such choices, it is in this context that people first tried to count the number of possibilities of building models (under all these assumptions, though) and found these large finite numbers such as the meanwhile proverbial number (coming from an estimate of the number of non-trivial cycles in a generic Calabi-Yau and the number of choices of periods of the “flux” fields) which then led them to speak of the “landscape of string theory vacua”. (Which of course without making a bunch of assumptions is vastly bigger, even.)
Due to the relation between supersymmetry and Calabi-Yau manifolds, of particular interest is the case of F/M-theory on elliptically fibered Calabi-Yau 4-folds, see there for more.
For references see below at References - Models in type II string theory
Computer scan of Gepner-model compactifications
Discussion of string phenomenology of intersecting D-brane models KK-compactified with non-geometric fibers such that the would-be string sigma-models with these target spaces are in fact Gepner models (in the sense of Spectral Standard Model and String Compactifications) is in (Dijkstra-Huiszoon-Schellekens 04a, Dijkstra-Huiszoon-Schellekens 04b):
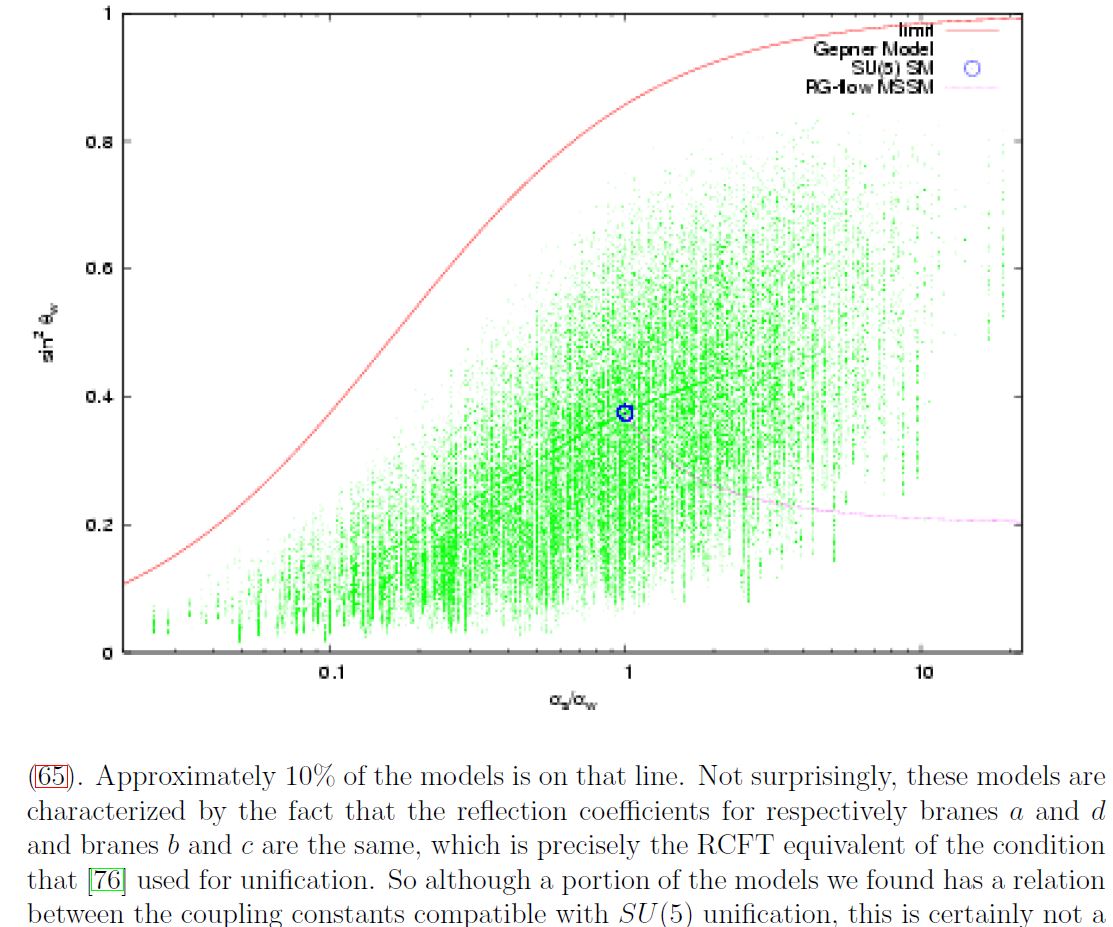
A plot of standard model-like coupling constants in a computer scan of Gepner model-KK-compactification of intersecting D-brane models according to Dijkstra-Huiszoon-Schellekens 04b.
The blue dot indicates the couplings in -GUT theory. The faint lines are NOT drawn by hand, but reflect increased density of Gepner models as seen by the computer scan.
Models in M-theory
The lift of the heterotic models compactified on Calabi-Yau manifolds to 11-dimensional supergravity with some of its “M-theory”-corrections taken into account is M-theory on G₂-manifolds, hence M-theory KK-compactified on G₂-manifolds (or rather: orbifolds) of, necessarily, dimension 7.
Accordingly, models in this context go by the name G₂-MSSM.
See at References - Models in M-theory.
Non-supersymmetric models
All of the above models aim for supersymmetry in the low-energy effective field theory, because it was a wide-spread thought that this is what describes the observable world at electroweak symmetry breaking-scale. However, new experimental results at the LHC make this low energy supersymmetry scenario increasingly unlikely (even if not fully ruled out yet). Accordingly people start to look for string models now that do not display low energy supersymmetry (of course all of them have high energy local supersymmetry, in that they are theories of supergravity).
See for instance (MRS 09) and citations given there.
Related concepts
-
string theory FAQ - Did string theory provide any insight relevant in experimental particle physics?
References
Surveys
Useful broad survey is in
- Fernando Marchesano, String phenomenology today, talk at StringPheno14 (pdf)
Technical surveys on particle physics string phenomenology include
-
Hans-Peter Nilles, String phenomenology (2004) (pdf)
-
Michael Dine, Supersymmetry and string theory: beyond the standard model, Cambridge University Press (2006, 2007) [ISBN:9781009290920, pdf]
-
Ralph Blumenhagen, Boris Kors, Dieter Lüst, Stephan Stieberger, Four-dimensional String Compactifications with D-Branes, Orientifolds and Fluxes, Phys.Rept.445:1-193,2007 (arXiv:hep-th/0610327)
-
Michael Douglas et. al. (eds.), String theory and the real world, Les Houches Session LXXXVII 2007
-
Tatsuo Kobayashi, String phenomenology 2009 (pdf slides)
-
Washington Taylor, TASI Lectures on Supergravity and String Vacua in Various Dimensions (arXiv:1104.2051)
-
Bobby Acharya, Gordon Kane, Piyush Kumar, Compactified String Theories – Generic Predictions for Particle Physics (arXiv:1204.2795)
-
Luis Ibáñez, Angel Uranga, String Theory and Particle Physics – An Introduction to String Phenomenology, Cambridge University Press 2012
-
Martin Wijnholt, String compactification, PITP 2014 lecture notes (pdf, slides for lecture 1, slides for lecture 2, slides for lecture 3)
-
Eran Palti, Review of Model Building in String Theory, talk at String Phenomenology 2014 (pdf)
-
Fernando Marchesano, Gary Shiu, Timo Weigand, The Standard Model from String Theory: What Have We Learned? [arXiv:2401.01939]
Technical surveys on cosmological string phenomenology include
- S. F. King, J. P. Roberts, Natural Dark Matter from Type I String Theory (arXiv:hep-ph/0608135)
The “bottom-up approach” to string model building is attributed to
- G. Aldazabal, Luis Ibáñez, F. Quevedo, Angel Uranga, D-Branes at Singularities : A Bottom-Up Approach to the String Embedding of the Standard Model, JHEP 0008:002 2000 (arXiv:hep-th/0005067)
See also
- Hans-Peter Nilles, Patrick K.S. Vaudrevange, Geography of Fields in Extra Dimensions: String Theory Lessons for Particle Physics, Perspectives on String Phenomenology“ (World Scientific) (arXiv:1403.1597)
For Gepner models:
- Christian Reppel, Phenomenological Aspects of Gepner Models, 2007 (pdf)
Original articles
-
Philip Candelas, Gary Horowitz, Andrew Strominger, Edward Witten, Vacuum configurations for superstrings, Nuclear Physics B Volume 258, 1985, Pages 46-74 Nucl. Phys. B 258, 46 (1985) (doi:10.1016/0550-3213(85)90602-9)
-
Bobby Acharya, Edward Witten, Chiral Fermions from Manifolds of Holonomy (arXiv:hep-th/0109152)
-
Cumrun Vafa, The String Landscape and the Swampland (arXiv:hep-th/0509212)
Heterotic string phenomenology
The historical origin of all string phenomenology is the top-down GUT-model building in heterotic string theory due to
- Philip Candelas, Gary Horowitz, Andrew Strominger, Edward Witten, Vacuum configurations for superstrings, Nuclear Physics B Volume 258, 1985, Pages 46-74 Nucl. Phys. B 258, 46 (1985) [doi:10.1016/0550-3213(85)90602-9]
Review and exposition:
-
Edward Witten, Quest For Unification, Heinrich Hertz lecture at SUSY 2002 at DESY, Hamburg [arXiv:hep-ph/0207124]
-
Hans-Peter Nilles, Strings, Exceptional Groups and Grand Unification, talk at Planck 2011 [pdf, pdf]
-
Saul Ramos-Sanchez, Michael Ratz, Heterotic Orbifold Models, in Handbook of Quantum Gravity, Springer (2024) [doi:10.1007/978-981-19-3079-9,
Database of heterotic string vacua via stable vector bundles on Calabi-Yau 3-folds:
- Maxime Gabella, Yang-Hui He, Andre Lukas: An Abundance of Heterotic Vacua, Journal of High Energy Physics, 2008 JHEP12 (2008) [doi:10.1088/1126-6708/2008/12/027, arXiv:0808.2142]
The -heterotic string
The following articles claim the existence of exact realization of the gauge group and matter-content of the MSSM in heterotic string theory on orbifolds (not yet checking Yukawa couplings):
-
Volker Braun, Yang-Hui He, Burt Ovrut, Tony Pantev, A Heterotic Standard Model, Phys. Lett. B618 : 252-258 2005 (arXiv:hep-th/0501070)
-
Wilfried Buchmuller, Koichi Hamaguchi, Oleg Lebedev, Michael Ratz, Supersymmetric Standard Model from the Heterotic String, Phys. Rev. Lett. 96 121602 (2006) ([doi:varXiv:hep-ph/0511035]
-
Volker Braun, Yang-Hui He, Burt Ovrut, Tony Pantev, The Exact MSSM Spectrum from String Theory, JHEP 0605:043, 2006 (arXiv:hep-th/0512177)
-
Vincent Bouchard, Ron Donagi, An SU(5) Heterotic Standard Model, Phys. Lett. B633:783-791,2006 (arXiv:hep-th/0512149)
A computer search through the “landscape” of Calabi-Yau varieties showed severeal hundreds more such exact heterotic standard models (about one billionth of all CYs searched, and most of them arising as SU(5)-GUTs):
general computational theory:
- Lara Anderson, Yang-Hui He, Andre Lukas, Heterotic Compactification, An Algorithmic Approach, JHEP 0707:049, 2007 (arXiv:hep-th/0702210)
using heterotic line bundle models:
-
Lara Anderson, James Gray, Andre Lukas, Eran Palti, Two Hundred Heterotic Standard Models on Smooth Calabi-Yau Threefolds, Phys. Rev. D 84, 106005 (2011) (arXiv:1106.4804)
-
Lara Anderson, James Gray, Andre Lukas, Eran Palti, Heterotic Line Bundle Standard Models JHEP06(2012)113 (arXiv:1202.1757)
-
Lara Anderson, Andrei Constantin, James Gray, Andre Lukas, Eran Palti, A Comprehensive Scan for Heterotic GUT models, JHEP01(2014)047 (arXiv:1307.4787)
-
Yang-Hui He, Seung-Joo Lee, Andre Lukas, Chuang Sun, Heterotic Model Building: 16 Special Manifolds, J. High Energ. Phys. 2014, 77 (2014) (arXiv:1309.0223)
-
Stefan Groot Nibbelink, Orestis Loukas, Fabian Ruehle, Patrick K.S. Vaudrevange, Infinite number of MSSMs from heterotic line bundles?, Phys. Rev. D 92, 046002 (2015) (arXiv:1506.00879)
-
Andreas Braun, Callum R. Brodie, Andre Lukas, Heterotic Line Bundle Models on Elliptically Fibered Calabi-Yau Three-folds, JHEP04 (2018) 087 (arXiv:1706.07688)
-
Andrei Constantin, Yang-Hui He, Andre Lukas, Counting String Theory Standard Models, Physics Letters B
Volume 792, 10 May 2019, Pages 258-262 (arXiv:1810.00444)
-
Alon E. Faraggi, Glyn Harries, Benjamin Percival, John Rizos, Towards machine learning in the classification of orbifold compactifications (arXiv:1901.04448)
-
Magdalena Larfors, Robin Schneider, Explore and Exploit with Heterotic Line Bundle Models, Fortschritte der Physik Vol 86 Nr. 5 (arXiv:2003.04817)
The resulting database of heterotic line bundle models is here:
- Lara Anderson, James Gray, Andre Lukas, Eran Palti, Heterotic standard model database (web)
Review includes
-
Lara Anderson, New aspects of heterotic geometry and phenomenology, talk at Strings2012, Munich 2012 (pdf)
-
Yang-Hui He, Deep-learning the landscape, talk at String and M-Theory: The new geometry of the 21st century (pdf slides, video recording)
-
Yang-Hui He, Calabi-Yau Spaces in the String Landscape (arXiv:2006.16623)
Computation of metrics on these Calabi-Yau compactifications (eventually needed for computing their induced Yukawa couplings) is started in
- Volker Braun, Tamaz Brelidze, Michael Douglas, Burt Ovrut, Calabi-Yau Metrics for Quotients and Complete Intersections, JHEP 0805:080, 2008 (arXiv:0712.3563)
and via machine learning:
-
Andrei Constantin, Cristofero S. Fraser-Taliente, Thomas R. Harvey, Andre Lukas, Burt Ovrut, Computation of Quark Masses from String Theory [arXiv:2402.01615]
-
Per Berglund, Giorgi Butbaia, Tristan Hübsch, Vishnu Jejjala, Damián Mayorga Peña, Challenger Mishra, Justin Tan: Precision String Phenomenology [arXiv:2407.13836]
This “heterotic standard model” has a “hidden sector” copy of the actual standard model, more details of which are discussed here:
- Volker Braun, Yang-Hui He, Burt Ovrut, Supersymmetric Hidden Sectors for Heterotic Standard Models (arXiv:1301.6767)
The issue of moduli stabilization in these kinds of models is discussed in
-
Michele Cicoli, Senarath de Alwis, Alexander Westphal, Heterotic Moduli Stabilization (arXiv:1304.1809)
-
Lara Anderson, James Gray, Andre Lukas, Burt Ovrut, Vacuum Varieties, Holomorphic Bundles and Complex Structure Stabilization in Heterotic Theories (arXiv:1304.2704)
Principles singling out heterotic models with three generations of fundamental particles are discussed in:
- Philip Candelas, Xenia de la Ossa, Yang-Hui He, Balazs Szendroi, Triadophilia: A Special Corner in the Landscape, Adv.Theor.Math.Phys.12:2,2008 (arXiv:0706.3134)
Discussion of non-supersymmetric: GUT models:
- Alon E. Faraggi, Viktor G. Matyas, Benjamin Percival, Classification of Non-Supersymmetric Pati-Salam Heterotic String Models (arXiv:2011.04113)
See also:
- Carlo Angelantonj, Ioannis Florakis, GUT Scale Unification in Heterotic Strings, Physics Letters B 789 (2019) 496-501 [doi:10.1016/j.physletb.2018.12.054arXiv:1812.06915]
The -heterotic string
Discussion of string phenomenology for the SemiSpin(32)-heterotic string (see also at type I phenomenology):
-
Kang-Sin Choi, Stefan Groot Nibbelink, Michele Trapletti, Heterotic model building in four dimensions, JHEP 0412:063, 2004 (arXiv:hep-th/0410232)
-
Hans-Peter Nilles, Saul Ramos-Sanchez, Patrick K.S. Vaudrevange, Akin Wingerter, Exploring the Heterotic String, JHEP 0604:050 (2006) [doi:10.1088/1126-6708/2006/04/050arXiv:hep-th/0603086]
-
Saul Ramos-Sanchez, Towards Low Energy Physics from the Heterotic String, Fortsch. Phys. 10 (2009) 907-1036 [doi:10.1002/prop.200900073arXiv:0812.3560]
-
Naoki Yamatsu, String-Inspired Special Grand Unification, Progress of Theoretical and Experimental Physics, Volume 2017, Issue 10, 1 (arXiv:1708.02078, doi:10.1093/ptep/ptx135)
-
Jihn E. Kim, Grand unfication models from heterotic string (arXov:2008.00367)
On heterotic line bundle models:
- Hajime Otsuka, heterotic line bundle models, (arXiv:1801.03684)
The “”-heterotic string
This non-supersymmetric string theory was first described in:
-
Luis Alvarez-Gaumé, Paul Ginsparg, Gregory Moore and Cumrun Vafa, An heterotic string, Phys. Lett. B 171 (1986) 155 [doi:10.1016/0370-2693(86)91524-8]
-
Lance Dixon and Jeffrey Harvey, String Theories in Ten-Dimensions Without Space-Time Supersymmetry, Nucl. Phys. B 274 (1986) 93 [doi:10.1016/0550-3213(86)90619-X]
A proposal on what the correct global character of the gauge group is appears in:
- Brett McInnes, The Semispin Groups in String Theory, J. Math. Phys. 40 (1999) 4699-4712 [arXiv:hep-th/9906059, doi:10.1063/1.532999]
A suggestion that the heterotic string is a the string “minus” the semispin group :
- Adrian Norbert Schellekens, and Nicholas Warner Anomalies, characters and strings, Nuclear Physics B 287 (1987) 317-361 [doi:10.1016/0550-3213(87)90108-8]
Further Models
Type II string theory models
The canonical textbook for type II superstring phenomenology via intersecting D-brane models is
The bottom-up intersecting D-brane model building originates with
See also
- Frederik Denef, Les Houches Lectures on Constructing String Vacua, in String theory and the real world (arXiv:0803.1194)
Reviews of intersecting D-brane model in type II string theory (in orientifold flux compactifications) include
-
Dieter Lüst, Intersecting Brane Worlds – A Path to the Standard Model ?, Class. Quant. Grav.21 : S1399-1424, 2004 (arXiv:hep-th/0401156)
-
Ralph Blumenhagen, Volker Braun, Boris Kors, Dieter Lüst, The Standard Model on the Quintic, Summary of Talks at SUSY02, 1st Intl. Conference on String Phenomenology in Oxford, Strings 2002 and 35th Ahrenshoop Symposium. (arXiv:hep-th/0210083)
-
Ralph Blumenhagen, Mirjam Cvetic, Paul Langacker, Gary Shiu, Towards Realistic Intersecting D-Brane Models, Ann. Rev. Nucl. Part. Sci. 55 (2005) 71-139 [arXiv:hep-th/0502005, doi:10.1146/annurev.nucl.55.090704.151541]
-
Ching-Ming Chen, Tianjun Li, Dimitri V. Nanopoulos, Standard-Like Model Building on Type II Orientifolds, Nucl.Phys.B732:224-242,2006 (arXiv:hep-th/0509059)
-
Angel Uranga, The standard model from D-branes in string theory, talk at Padova, January 2008 (pdf)
-
Matthew J. Dolan, Sven Krippendorf, Fernando Quevedo, Towards a Systematic Construction of Realistic D-brane Models on a del Pezzo Singularity, JHEP 1110 (2011) 024 (arXiv:1106.6039)
-
Anshuman Maharana, Eran Palti, Models of Particle Physics from Type IIB String Theory and F-theory: A Review (arXiv:1212.0555)
-
Fernando Marchesano, Bert Schellekens, Timo Weigand, D-brane and F-theory Model Building, in: Handbook of Quantum Gravity, Springer (2023) [arXiv:2212.07443]
Computer scan of Gepner model-KK-compactifications of intersecting D-brane models:
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Chiral Supersymmetric Standard Model Spectra from Orientifolds of Gepner Models, Phys.Lett. B609 (2005) 408-417 (arXiv:hep-th/0403196)
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Supersymmetric Standard Model Spectra from RCFT orientifolds, Nucl.Phys.B710:3-57,2005 (arXiv:hep-th/0411129)
Computer scan of toroidal orbifold-KK-compactification of intersecting D-brane models:
-
Ralph Blumenhagen, Florian Gmeiner, Gabriele Honecker, Dieter Lüst, Timo Weigand, The Statistics of Supersymmetric D-brane Models, Nucl.Phys.B713:83-135, 2005 (arXiv:hep-th/0411173)
-
Florian Gmeiner, Ralph Blumenhagen, Gabriele Honecker, Dieter Lüst, Timo Weigand, One in a Billion: MSSM-like D-Brane Statistics, JHEP 0601:004, 2006 (arXiv:hep-th/0510170)
Realistic Yukawa couplings and fermion masses in an MSSM Pati-Salam GUT model with 3 generations of fermions realized on intersecting D6-branes KK-compactified on a toroidal orbifold are claimed in
-
Ching-Ming Chen, Tianjun Li, Van Eric Mayes, Dimitri Nanopoulos, A Realistic World from Intersecting D6-Branes, Phys.Lett.B665:267-270, 2008 (arXiv:hep-th/0703280, doi:10.1016/j.physletb.2008.06.024)
-
Ching-Ming Chen, Tianjun Li, Van Eric Mayes, Dimitri Nanopoulos, Realistic Yukawa Textures and SUSY Spectra from Intersecting Branes, Phys.Rev.D77:125023, 2008 (arXiv:0711.0396)
-
Van Eric Mayes, All Fermion Masses and Mixings in an Intersecting D-brane World (arXiv:1902.00983)
-
Jordan Gemmill, Evan Howington, Van Eric Mayes, One String to Rule Them All: Neutrino Masses and Mixing Angles (arXiv:1907.07106)
-
Tianjun Li, Adeel Mansha, Rui Sun, Revisiting the Supersymmetric Pati-Salam Models from Intersecting D6-branes (arXiv:1910.04530)
-
Tianjun Li, Adeel Mansha, Rui Sun, Generalized Supersymmetric Pati-Salam Models from Intersecting D6-branes (arXiv:1912.11633)
See also
- Erik Parr, Patrick K.S. Vaudrevange, Martin Wimmer, Predicting the orbifold origin of the MSSM (arXiv:2003.01732)
Type I string theory model
Discussion for type I string theory:
-
H.S. Mani, A. Mukherjee, R. Ramachandran, A.P. Balachandran, Embedding of GUT in superstring theories, Nuclear Physics B Volume 263, Issues 3–4, 27 January 1986, Pages 621-628 (arXiv:10.1016/0550-3213(86)90277-4)
-
Luis Ibáñez, C. Muñoz, S. Rigolin, Aspects of Type I String Phenomenology, Nucl.Phys. B553 (1999) 43-80 (arXiv:hep-ph/9812397)
-
Emilian Dudas, Theory and Phenomenology of Type I strings and M-theory, Class. Quant. Grav.17:R41-R116, 2000 (arXiv:hep-ph/0006190)
-
Naoki Yamatsu, String-Inspired Special Grand Unification (arXiv:1708.02078)
F-Theory models
Discussion of GUT models via F-theory is in
- Chris Beasley, Jonathan Heckman, Cumrun Vafa, GUTs and Exceptional Branes in F-theory - I (arxiv:0802.3391), II: Experimental Predictions (arxiv:0806.0102)
A direct geometric engineering of the MSSM within F-theory is claimed in
- Mirjam Cvetič, Ling Lin, Muyang Liu, Paul-Konstantin Oehlmann, An F-theory Realization of the Chiral MSSM with -Parity (arXiv:1807.01320)
Discussion of the exact gauge group of the standard model of particle physics, including its -quotient (see there) and the exact fermion field content, realized in F-theory is in
-
Denis Klevers, Damian Kaloni Mayorga Pena, Paul-Konstantin Oehlmann, Hernan Piragua, Jonas Reuter, F-Theory on all Toric Hypersurface Fibrations and its Higgs Branches, JHEP01(2015)142 (arXiv:1408.4808)
-
Mirjam Cvetic, Ling Lin, section 3.3 of The global gauge group structure of F-theory compactifications with s (arXiv:1706.08521)
Based on this, a large number of realizations of the exact field content of the standard model of particle physics (or rather the MSSM) in F-theory is claimed to be realized in
-
Mirjam Cvetic, James Halverson, Ling Lin, Muyang Liu, Jiahua Tian, A Quadrillion Standard Models from F-theory (arXiv:1903.00009)
-
Washington Taylor, Andrew P. Turner, Generic construction of the Standard Model gauge group and matter representations in F-theory (arXiv:1906.11092)
Realization of -GUT models in F-theory:
- Shing Yan Li, Washington Taylor, Towards natural and realistic GUTs in F-theory [arXiv:2401.00040]
Review:
- Fernando Marchesano, Bert Schellekens, Timo Weigand, D-brane and F-theory Model Building, in Handbook of Quantum Gravity, Springer (2023) [arXiv:2212.07443]
M-theory models
A comprehensive account on models in M-theory on G₂-manifolds and the G₂-MSSM is in
-
Bobby Acharya, Konstantin Bobkov, Gordon Kane, Piyush Kumar, Jing Shao, The -MSSM - An Theory motivated model of Particle Physics (arXiv:0801.0478)
-
Bobby Acharya, Gordon Kane, Piyush Kumar, Compactified String Theories – Generic Predictions for Particle Physics, Int. J. Mod. Phys. A, Volume 27 (2012) 1230012 (arXiv:1204.2795)
-
Gordon Kane, String/M-theories About Our World Are Testable in the traditional Physics Way (arXiv:1601.07511, video recording)
with comments on comparison to more recent experiments in
- Gordon Kane, Ran Lu, Bob Zheng, Review and Update of the Compactified M/string Theory Prediction of the Higgs Boson Mass and Properties, Int. J. Mod. Phys. A Volume 28 (2013) 1330002 (arXiv:1211.2231)
Original articles include
-
Bobby Acharya, Konstantin Bobkov, Gordon Kane, Piyush Kumar, Jing Shao, Explaining the Electroweak Scale and Stabilizing Moduli in M Theory (arXiv:hep-th/0701034)
-
Bobby Acharya, Konstantin Bobkov, Gordon Kane, Piyush Kumar, Diana Vaman, An M theory Solution to the Hierarchy Problem (arXiv:hep-th/0606262)
-
Bobby Acharya, Konstantin Bobkov, Kähler Independence of the -MSSM, JHEP (arXiv:0810.3285)
See also
- Lara Anderson, Heterotic and M-theory Compactifications for String Phenomenology (arXiv:0808.3621)
Alternatively, discussion in Hořava-Witten theory:
- Burt Ovrut, Vacuum Constraints for Realistic Heterotic M-Theories (arXiv:1811.08892)
Heterotic M-theory models
Discussion in heterotic M-theory:
-
Ron Donagi, Burt Ovrut, Tony Pantev, Daniel Waldram, Standard Models from Heterotic M-theory, Adv. Theor. Math. Phys. 5 (2002) 93-137 (arXiv:hep-th/9912208)
-
Ron Donagi, Burt Ovrut, Tony Pantev, Daniel Waldram, Standard Model Vacua in Heterotic M-Theory, talk at Strings ‘99, Potsdam, Germany, 19 - 24 Jul 1999 (arXiv:hep-th/0001101)
and with emphasis on heterotic line bundle-models:
- Sebastian Dumitru, The strongly coupled heterotic string: Geometry & Phenomenology [arXiv:2206.12310]
See also:
- Cédric Deffayet, Burt Ovrut, Paul Steinhardt, Stable Vacua with Realistic Phenomenology and Cosmology in Heterotic M-theory Satisfying Swampland Conjectures [arXiv:2401.04828]
Non-supersymmetric models
A survey of string model buidling without low energy susy is in
- Emil Martinec, Daniel Robbins, Savdeep Sethi, Non-Supersymmetric String Theory (arXiv:0904.3498)
An old observation on string models without low energy susy, recently re-appreciated, is
- Keith Dienes, How Strings Make Do without Supersymmetry: An Introduction to Misaligned Supersymmetry (arXiv:hep-th/9409114)
A newer observation that received much more attention is
- Nima Arkani-Hamed, Savas Dimopoulos, Supersymmetric Unification Without Low Energy Supersymmetry And Signatures for Fine-Tuning at the LHC (arXiv:hep-th/0405159)
String Phenomenology conferences
-
String Phenomenology 2002 (home page)
-
String Phenomenology 2003 (home page)
-
String Phenomenology 2004 (home page)
-
String Phenomenology 2005 (home page)
-
String Phenomenology 2006 (home page)
-
String Phenomenology 2007 (home page)
-
String Phenomenology 2008 (home page)
-
String Phenomenology 2009 (home page)
-
String Phenomenology 2010 (home page)
-
String Phenomenology 2013 (home page)
-
String Phenomenology 2014 (home page)
-
String Phenomenology 2018 (home page)
-
String Phenomenology 2019 (home page)
String cosmic inflation
In string theory the inflaton field for models of cosmic inflation field can be modeled by various effects, such as
- open string stretching between D-brane-anti D-brane pairs.
For a review and further pointers to the literature see at
- Cliff Burgess, M. Cicoli, F. Quevedo, String Inflation After Planck 2013 (arXiv:1306.3512)
Axion phenomenology
On stringy axion phenomenology:
-
Joseph P. Conlon, M.C. David Marsh, Searching for a 0.1-1 keV Cosmic Axion Background (arXiv:1305.3603)
Primordial decays of string theory moduli at naturally generate a dark radiation Cosmic Axion Background (CAB) with energies. This CAB can be detected through axion-photon conversion in astrophysical magnetic fields to give quasi-thermal excesses in the extreme ultraviolet and soft X-ray bands. Substantial and observable luminosities may be generated even for axion-photon couplings . We propose that axion-photon conversion may explain the observed excess emission of soft X-rays from galaxy clusters, and may also contribute to the diffuse unresolved cosmic X-ray background. We list a number of correlated predictions of the scenario.
Last revised on July 18, 2024 at 12:52:37. See the history of this page for a list of all contributions to it.