nLab twistor space
Context
Higher spin geometry
spin geometry, string geometry, fivebrane geometry …
Ingredients
Spin geometry
rotation groups in low dimensions:
see also
String geometry
Fivebrane geometry
Ninebrane geometry
Quantum field theory
Contents
Idea
Twistor space in the original sense of (Penrose 67) is a complex manifold whose complex geometry is usefully related to the conformal geometry of (conformally compactified complexified) 4-dimensional Minkowski spacetime. The Penrose transform from twistor space to this spacetime yields powerful computational tools for studying certain quantum field theories, in particular 4d Yang-Mills theory. Notably it sends ordinary cohomology classes on twistor space to self-dual Yang-Mills fields on spacetime (Ward 77, Ward-Wells 90). Morever, when twistor space is taken as a target space for twistor string theory, then it serves to compute the MHV amplitudes in super Yang-Mills theory (Witten 03).
This Penrose transform is exhibited by a correspondence of coset spaces/flag varieties/Grassmannians which is a special case of general such correspondences as they are studied in Schubert calculus, geometric representation theory, parabolic geometry. Therefore one can consider “generalized twistors” to be elements of certain flag varieties and “generalized Penrose transforms” to be those induced by the relevant correspondences. (Baston-Eastwood 89, Cap 01).
In this generality given a semisimple Lie group and two parabolic subgroups and with intersection , then the twistor correspondence is the correspondence (see also at Schubert calculus – Correspondences and at horocycle correspondence) of the form
given by the projections onto the two coset spaces/flag varieties and a Penrose transform is an integral transform/pull-push through this correspondence.
In particular there are higher twistor spaces corresponding to higher dimensional Minkowski spacetimes which are useful for describing higher dimensional quantum field theory, notably there are twistor spaces for 6-dimensional spacetime useful for the study of the 6d (2,0)-superconformal QFT on the worldvolume of the M5-brane (MREIC 11) with its self-dual higher gauge field, the B-field .
The original twistor correspondence (Penrose 67) is the correspondence
where
-
the Grassmannian of planes in complexified 4d Minkowski spacetime;
-
the twistor space is the complex projective 3-space ;
-
the correspondence space is the space of lines in planes in .
(e.g. Ward-Wells 90)
Details
Twistors for 4d Minkowski space
We discuss the original twistors for the description of physics in 4d Minkowski spacetime. In summary, twistor space of 4d Minkowski space is the space of pairs consisting of a momentum vector and an angular momentum tensor subject to the constraint that the momentum is lightlike and of definite helicity.
The formulation is all motivated from the form that basic quantities of special relativistic physics take when vectors are expressed in spinor coordinates via the exceptional spin isomorphism
Under this identification a chiral spinor is represented just by a pair of complex numbers and one may write the spinor as
Moreover, via the non-degenerate bilinear pairing
given by the Clifford algebra (see at spin representation for details) one can express vectors
in Minkowski spacetime as “bi-spinors” given by 2x2 Hermitean matrices
where denote the generators of the Clifford algebra given by the Pauli matrices.
This is such that the Lorentz metric norm is just the determinant of this matrix
This spinorial re-expression of vectors turns out to yield very efficient expressions particularly for those kinds of terms that appear in the observed physics of massless chiral particles, such as they appear in the standard model of particle physics.
For instance a skew rank-2 tensor (2-from) with (for instance the field strength of an electromagnetic field) has spinorial expression of the simple form
for complex numbers and . Here if itself is real-number valued, then is the complex conjugate of and hence any real 2-form is encoded equivalently by a bispinor via
Crucially the Hodge dual of a 2-form has then the simple expression
which is the first sign that self-dual Yang-Mills theory has a simpler expression in terms of such spinorial coordinates.
Now characterizing an elementary particle is (by the discussion at unitary representation of the Poincaré group) the momentum 4-vector and its angular momentum tensor . A twistor is effectively a pair of spinorial coordinates expression this data for massless and chiral particles.
Here chiral means this: from combining the momentum and angular momentum one obtains the Pauli-Lubanski vector
and chiral particles satisfy
for some constant .
A twistor is a set of spinorial coordinates for encoding tensors which satisfy
-
masslessness:
-
chirality .
By the discussion at celestial sphere we have that the first condition means equivalently that there is a single spinor such that the spinorial expression for the momentum is
By the above discussion of 2-forms we know moreover that is encoded by a bispinor and imposing the chirality constraint one finds, using the above formula for the Hodge dual, that its solutions are parameterized precisely by another spinor via
(where the parenthesis denote symmetrization of indices).
In summary, the possible momentum and angular momentum of massless chiral particles in 4d Minkowski spacetime is parameterized precisely by pair of spinors
The image of this under modding out by a global complex factor is a Penrose twistor
an element of the complex projective 3-space, called twistor space.
Twistor space
To discuss twistor space for Minkowski spacetime, it is useful to work more generally with -dimensional Minkowski spacetime for . If we also use the corresponding irreducible real spin representation then by the discussion there, these are equivalently 2-component vectors over the real normed division algebras , respectively. (See also at supersymmetry and division algebra, we follow Bengtsson-Cederwall 88).
With this, the vector space underlying -dimensional Minkowski spacetime is identified with the space of hermitian matrices with entries in
and the Minkowski metric norm-square is then identified with the determinant of matrices:
A choice of linear basis for this space is provided by the Pauli matrices with coefficients in , namely the matrices
where denotes an orthonormal basis for the elements of . Here we write
for the operation of complex conjugation in , i.e. the -linear operation which sends the unit to itself, and sends imaginary elements to their negative.
In terms of this basis then a -component vector is identified with the hermitian matrix
This presentation of Minkowski spacetime by hermitian matrices with coefficients in makes it very natural to consider also its “-ification” (hence complexification in the case that and ), namely the space of all matrices with entries in :
This space carries the operation of Hermitian conjugation
as an involution, and ordinary -dimensional Minkowski spacetime is hence the fixed point set of this involution.
By the discussion there, the Spin-invariant pairing of two real spinors to a vector is given by (prop.)
In particular the pairing of a spinor with itself is
Since, as hermitian matrices, the matrices arising this way are manifestly precisely the hermitian projection operators on 1-dimensional linear subspaces of , these are precisely the hermitian matrices with vanishing determinant. Hence the future-oriented lightlike vectors in Minkowski spacetime in are precisely those that arise as the pairing of a chiral spinor with itself.
The above formula shows that as we rescale with , then the corresponding lightlike vector is sent to itself, rescaled by the real number . Hence the direction of lightlike vectors is parameterized by the projective space . At least for (the complex numbers) this is called the celestial sphere (in this case: the Riemann sphere ).
Lightlike vectors in up to scale are equivalently loci of lightlike geodesics through the origin. A general lightlike geodesic in is instead parameterized by
for some offset . To encode this offset into spinors, consider the image of under the Clifford action with :
This relation bewteen and is called the incidence relation in this context.
The locus of the lightlike geodesic does not change as we rescale by elements , and then gets rescaled accordingly. Hence the pair regarded as encoding lightlike geodesics in Minkowski spacetime should be thought of as an element of the projective space
This is the twistor space corresponding to the given Minkowski spacetime.
However, by the above definition of , not every element of this space corresponds to a lightlike geodesic. Rather (for ) it is only those satisfying
reflecting the fact that is a hermitian matrix, instead of a general matrix. (For there is no elegant statement like this, due to the non-associativity of the octonions . But there is nevertheless an analogue of the twistor transform in 10d Witten 86).
Hence the subspace inclusion
of Minkowski-spacetime into its -ification, corresponds to a subspace
of twistor space. This is called the space of null twistors, or the spin shell.
If we consider the metric on given in component by
then this subspace is the quadric given by the equation
Now conversely, given not equal to zero and satisfying this condition in that there is a hermitian with , then also every hermitian matrix of the form
(for , hence every point on the lightlike geodesic through in the direction of ) satisfies the relation (since the spinor index is raised with , which is skew symmetric). This way non-zero points in correspond to lightlike geodesics in Minkowski spacetime.
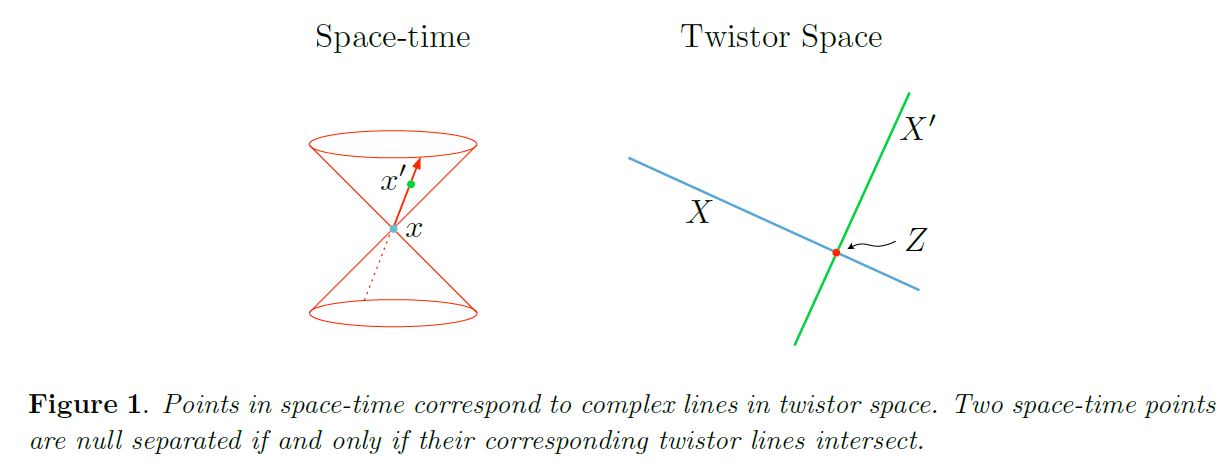
(graphics from Adamo 13)
This correspondence extends also to the 0-point in if one passes to “compactified Minkowski spacetime”, given by the Grassmannian of complex planes in (review includes Fioresi-Lledo-Varadarajan 07, section 2).
Related concepts
-
A real analog of this is the Radon transform.
References
General
The notion originates in
-
Roger Penrose, Twistor algebra, Journal of Mathematical Physics 8 (2): 345–366, (1967) (doi:10.1063/1.1705200)
-
Roger Penrose, The twistor programme, Reports on Mathematical Physics 12 (1): 65–76 (1977)
Key developments concerning scattering amplitudes are due to
- Andrew Hodges, Twistor diagrams (web)
The relation to self-dual Yang-Mills theory is due to
- R. S. Ward, On Selfdual gauge fields, Phys. Lett. A61 (1977) 81-82.
Introductions and surveys:
-
Yuri Manin, chapters 1 and 2 of Gauge Field Theory and Complex Geometry, Grundlehren der Mathematischen Wissenschaften 289, Springer 1988
-
Paul Bair, Introduction to twistors (pdf)
-
S. A. Huggett, K. P. Todd, An introduction to twistor theory, Cambridge University Press (1985)
-
Liana David, The Penrose transform and its applications, 2001 (pdf)
-
Maciej Dunajski, Twistor theory and differential equations, J.Phys. A42:404004 (2009) arXiv:0902.0274 doi
-
Roger Penrose, Twistor theory, talk at New Spaces for Mathematics and Physics, IHP Paris, 2015 (video recording)
-
R. Fioresi, M. A. Lledo, Veeravalli Varadarajan, The Minkowski and conformal superspaces, J.Math.Phys.48:113505,2007 (arXiv:0609813)
-
Michael Atiyah, Maciej Dunajski, Lionel J. Mason, Twistor theory at fifty: from contour integrals to twistor strings, Proc. R. Soc. A473: 20170530 (arXiv:1704.07464, doi:10.1098/rspa.2017.0530)
-
Tim Adamo, Lectures on twistor theory (arXiv:1712.02196)
-
Lionel J. Mason, N. M. J. Woodhouse, Integrability, self-duality and twistor theory, OUP 1996
-
R. S. Ward, R. O. Wells, Jr. Twistor geometry and field theory, Cambridge Univ. Press 1990
-
Roger Penrose, Twistor Theory: A Geometric Perspective for Describing the Physical World (doi:10.1017/9781108854399.011), chapter in: Gabriel Catren, Mathieu Anel (eds.) New Spaces for Mathematics and Physics, Cambridge University Press (2021) (doi:10.1017/9781108854429)
Review of the application in super Yang-Mills theory includes
- Tim Adamo, Twistor actions for gauge theory and gravity (arXiv:1308.2820)
See also
- Wikipedia, Twistor theory
Relation to geometric representation theory and parabolic geometry
A discussion in the general context of geometric representation theory is in
- Robert J. Baston, Michael G. Eastwood, The Penrose transform its interaction with representation theory Oxford Science Publications, Clarendon Press, 1989 (ISBN:9780198535652, spire:290342, pdf)
and the further generalization to Cartan geometry/parabolic geometry is discussed in
- Andreas Čap, Correspondence spaces and twistor spaces for parabolic geometries, J. Reine Angew. Math. 582 (2005) 143-172 (arXiv:math/0102097)
Palatial twistor theory
- Roger Penrose, Palatial twistor theory and the twistor googly problem, Phil. Trans. Royal Soc. A373: 20140237 (2015) doi
- R. Penrose, Twistor theory as an approach to fundamental physics, in: Foundations of mathematics and physics one century after Hilbert, 253-285 (2018), ed. Joseph Kouneiher doi
Application to quantum field theory
More on traditional applications to quantum field theory is in
- R.S. Ward, R.O. Wells, Twistor geometry and field theory, Cambridge Univ. Press 1990 (doi:10.1017/CBO9780511524493)
The relation of twistor geometry to MHV amplitudes in 4d Yang-Mills theory and twistor string theory is due to
- Edward Witten, Perturbative Gauge Theory As A String Theory In Twistor Space, Commun. Math. Phys. 252:189-258, 2004 (arXiv:hep-th/0312171)
Surveys of the resulting modern application of twistors in field theory include
- David Skinner, The geometry of scattering amplitudes, talk notes, November 2009 (pdf)
Twistors in higher dimensions
Discussion of twistors in dimensions 3,4,6 and 10 using the normed division algebras (as in supersymmetry and division algebras) is in
-
Ingemar Bengtsson, Martin Cederwall, Particles, Twistors and the Division Algebras, Nucl.Phys. B302 (1988) 81-103 (spire:247269, doi:10.1016/0550-3213(88)90667-0)
-
Martin Cederwall, Introduction to Division Algebras, Sphere Algebras and Twistors (arXiv:hep-th/9310115)
and specifically for dimension 10
- Edward Witten, Twistor-like transform in ten dimensions, Nuclear Physics B266:2, 245-264. (1986) (10.1016/0550-3213(86)90090-8)
and its AdS version:
- Alex Arvanitakis, Alec E. Barns-Graham, Paul Townsend, Twistor description of spinning particles in AdS, JHEP 01 (2018) 059 (arXiv:1710.09557)
Application to the 6d self-dual 2-form field
A general discussion of Penrose-Ward-type transforms sending circle 2-bundles (holomorphic line 2-bundles) on some twistor space to circle 2-bundles with connection and self-dual curvature 3-form on spacestime (expected to play a role in the description of the 6d (2,0)-superconformal QFT) is in
-
David Chatterjee, sections 4 and 8 of On gerbs, 1998 (pdf)
-
Lionel J. Mason, R. A. Reid-Edwards, A. Taghavi-Chabert, appendix of Conformal field theories in six-dimensional twistor space, J. Geom. Phys. 62 (2012), no. 12, 2353-2375 (arXiv:1111.2585)
- Christian Saemann, Martin Wolf, On twistors and conformal field theories from six dimensions, J. Math. Phys. 54:013507, 2013 (arXiv.1111.2539)
More generally, there are arguments that the worldvolume theory of several coincident M5-branes carries not just an abelian but a nonabelian higher gauge field given by a principal 2-bundle principal 2-connection.
The idea of generalizing the Penrose-Ward transform to one that takes nonabelian principal 2-bundles to self-dual principal 2-connections is explored in
- Christian Saemann, Martin Wolf, Six-dimensional superconformal field theories from principal 3-bundles over twistor space (arXiv:1305.4870)
Last revised on July 9, 2023 at 14:30:57. See the history of this page for a list of all contributions to it.