nLab Wilson loop
Context
-Chern-Weil theory
Ingredients
Connection
Curvature
Theorems
Differential cohomology
Ingredients
Connections on bundles
Higher abelian differential cohomology
Higher nonabelian differential cohomology
Fiber integration
Application to gauge theory
Contents
Idea
A Wilson loop or Wilson line is an observable in (both classical and quantum) gauge theory obtained from the holonomy of the gauge connection.
Hence if the gauge connection is given by a globally defined 1-form , then the Wilson loop along a closed loop is the trace of the path-ordered exponential
where is the “path-ordering operator” and are the components of the connection.
Properties
Relation to 1d Chern-Simons theory
For a suitable Lie group (compact, semi-simple and simply connected) the Wilson loops of -principal connections are equivalently the partition functions of a 1-dimensional Chern-Simons theory.
This appears famously in the formulation of Chern-Simons theory with Wilson lines. More detailes are at orbit method.
As the universal Vassiliev invariant
The un-traced Wilson loop observable of perturbative Chern-Simons theory is the universal Vassiliev invariant (see there for more):
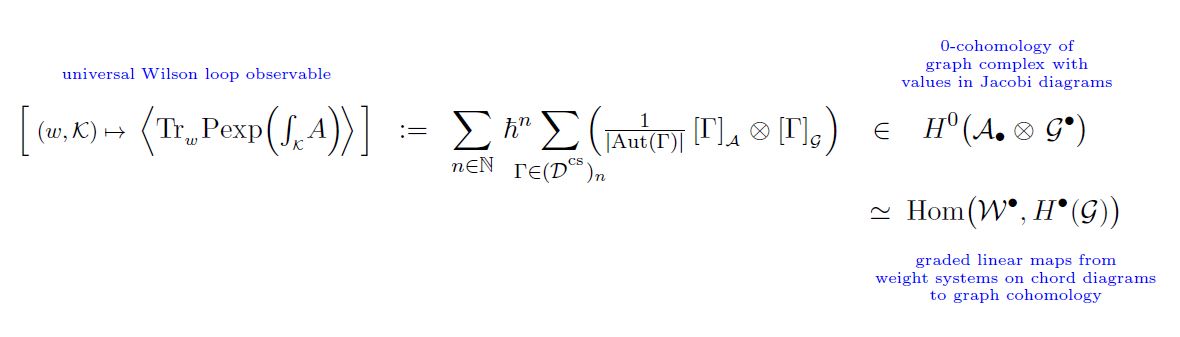

from Sati-Schreiber 19c
Relation to defects
Wilson loop insertions may be thought of or at least related to defects in the sense of QFT with defects.
Duality with ‘t Hooft operators under S-duality and geometric Langlands
S-duality of 4d super Yang-Mills theory may exchange Wilson loop operators with 't Hooft operators, in an incarnation of the geometric Langlands correspondence (Kapustin-Witten 06)
Examples
In Chern-Simons theory
In -Chern-Simons theory the Wilson line observables compute the Jones polynomial of the given curve. See there for more details.
In Rozansky-Witten theory
Proposition
(Rozansky-Witten Wilson loop of unknot is square root of A-hat genus)
For a hyperkähler manifold (or just a holomorphic symplectic manifold) the Rozansky-Witten invariant Wilson loop observable associated with the unknot in the 3-sphere is the square root of the A-hat genus of .
This is Roberts-Willerton 10, Lemma 8.6, using the Wheels theorem and the Hitchin-Sawon theorem.
Related entries
References
General
-
Kenneth Wilson, Confinement of quarks, Physical Review D 10 (8): 2445. doi (1974)
-
Yuri Makeenko, Methods of contemporary gauge theory, Cambridge Monographs on Math. Physics, Cambridge University Press (2002) [doi:10.1017/CBO9780511535147, gBooks]
-
Wikipedia Wilson loop
-
R. Giles, Reconstruction of gauge potentials from Wilson loops, Physical Review D 24 (8): 2160, doi
-
A. Andrasi, J. C. Taylor, Renormalization of Wilson operators in Minkowski space, Nucl. Phys. B516 (1998) 417, hep-th/9601122
-
Amit Sever, Pedro Vieira, Luis F. Alday, Juan Maldacena, Davide Gaiotto, An Operator product expansion for polygonal null Wilson loops, arxiv.org/abs/1006.2788
On super-Wilson lines via integration over supermanifolds:
- C.A. Cremonini, Pietro Grassi, S. Penati, Supersymmetric Wilson Loops via Integral Forms (arXiv:2003.01729)
In Chern-Simons theory
See at perturbative quantization of 3d Chern-Simons theory/Vassiliev knot invariants.
Relation between Dehn surgery and Wilson loop observables in Chern-Simons theory:
-
E. Guadagnini, Surgery rules in quantum Chern-Simons field theory, Nuclear Physics B Volume 375, Issue 2, 18 May 1992, Pages 381-398 (doi:10.1016/0550-3213(92)90037-C)
-
Boguslaw Broda, Chern-Simons theory on an arbitrary manifold via surgery (arXiv:hep-th/9305051)
The Poisson bracket of Wilson line observables in 3d Chern-Simons theory was obtained in
- W. Goldman, Invariant functions on Lie groups and Hamiltonian flow of surface group representations, Inventiones Math., 85 (1986), 263–302.
For more see
- Razvan Gelca, Alejandro Uribe, section 4 of Quantum mechanics and non-abelian theta functions for the gauge group (arXiv:1007.2010)
In Chern-Simons theory as a topological string theory:
- Hirosi Ooguri, Cumrun Vafa, Knot Invariants and Topological Strings, Nucl. Phys. B 577:419-438, 2000 (arXiv:hep-th/9912123)
Jones polynomial as Wilson loop observables
The identification of the Jones polynomial with Wilson loop observables in Chern-Simons theory is due to
- Edward Witten, Quantum field theory and the Jones polynomial, Commun. Math. Phys. 121,351-399 (1989) (euclid.cmp/1104178138)
see also
- Jürg Fröhlich, C. King, The Chern-Simons theory and knot polynomials, Comm. Math. Phys.
Volume 126, Number 1 (1989), 167-199 (euclid.cmp/1104179728)
Lecture notes:
- Edward Witten, A New Look At The Jones Polynomial of a Knot, Clay Conference, Oxford, October 1, 2013 (pdf)
The categorification of this relation to an identification of Khovanov homology with observables in D=4 super Yang-Mills theory:
-
Edward Witten, Khovanov homology and gauge theory, arxiv/1108.3103
-
Edward Witten, Fivebranes and Knots (arXiv:1101.3216)
Lecture notes:
- Edward Witten, Khovanov Homology And Gauge Theory, Clay Conference, Oxford, October 2, 2013 (pdf)
See also
- Vaughan Jones, Index for subfactors, Invent. Math. 72, I (I983); A polynomial invariant for links via yon Neumann algebras, Bull. AMS 12, 103 (1985); Hecke algebra representations of braid groups and link polynomials, Ann. Math. 126, 335 (1987)
Wilson lines computing holographic entropy in
Discussion of BTZ black hole entropy and more generally of holographic entanglement entropy in 3d quantum gravity/AdS3/CFT2 via Wilson line observables in Chern-Simons theory:
-
Martin Ammon, Alejandra Castro, Nabil Iqbal, Wilson Lines and Entanglement Entropy in Higher Spin Gravity, JHEP 10 (2013) 110 (arXiv:1306.4338)
-
Jan de Boer, Juan I. Jottar, Entanglement Entropy and Higher Spin Holography in , JHEP 1404:089, 2014 (arXiv:1306.4347)
-
Alejandra Castro, Stephane Detournay, Nabil Iqbal, Eric Perlmutter, Holographic entanglement entropy and gravitational anomalies, JHEP 07 (2014) 114 (arXiv:1405.2792)
-
Mert Besken, Ashwin Hegde, Eliot Hijano, Per Kraus, Holographic conformal blocks from interacting Wilson lines, JHEP 08 (2016) 099 (arXiv:1603.07317)
-
Andreas Blommaert, Thomas G. Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Ashwin Dushyantha Hegde, Role of Wilson Lines in 3D Quantum Gravity, 2019 (spire:1763572)
-
Xing Huang, Chen-Te Ma, Hongfei Shu, Quantum Correction of the Wilson Line and Entanglement Entropy in the Chern-Simons Gravity Theory (arXiv:1911.03841)
-
Eric D'Hoker, Per Kraus, Gravitational Wilson lines in (arXiv:1912.02750)
-
Marc Henneaux, Wout Merbis, Arash Ranjbar, Asymptotic dynamics of gravity with two asymptotic regions (arXiv:1912.09465)
and similarly for 3d flat-space holography:
-
Arjun Bagchi, Rudranil Basu, Daniel Grumiller, Max Riegler, Entanglement entropy in Galilean conformal field theories and flat holography, Phys. Rev. Lett. 114, 111602 (2015) (arXiv 1410.4089)
-
Rudranil Basu, Max Riegler, Wilson Lines and Holographic Entanglement Entropy in Galilean Conformal Field Theories, Phys. Rev. D 93, 045003 (2016) (arXiv:1511.08662)
-
Wout Merbis, Max Riegler, Geometric actions and flat space holography (arXiv:1912.08207)
Discussion for 3d de Sitter spacetime:
- Alejandra Castro, Philippe Sabella-Garnier, Claire Zukowski, Gravitational Wilson Lines in 3D de Sitter (arXiv:2001.09998)
In QFT with defects
Relation to QFT with defects is discussed in
slide 17 of
- Constantin Bachas, Conformal defects in/and String theory (pdf)
slide 5 of
- Constantin Bachas, Conformal defects in gauged WZW models (pdf)
As partition functions of 1d Chern-Simons theory
Expression of Wilson loops as partition functions of 1-dimensional Chern-Simons theories by the orbit method (as used notably in Chern-Simons theory) is in section 4 of
- Chris Beasley, Localization for Wilson Loops in Chern-Simons Theory, in J. Andersen, H. Boden, A. Hahn, and B. Himpel (eds.) Chern-Simons Gauge Theory: 20 Years After, AMS/IP Studies in Adv. Math., Vol. 50, AMS, Providence, RI, 2011. (arXiv:0911.2687)
referring to
- S. Elitzur, Greg Moore, A. Schwimmer, Nathan Seiberg, Remarks on the Canonical Quantization of the Chern-Simons-Witten Theory, Nucl. Phys. B 326 (1989) 108–134.
in the context of Chern-Simons theory and in more general gauge theory to
- A. P. Balachandran, S. Borchardt, and A. Stern, Lagrangian And Hamiltonian Descriptions of Yang-Mills Particles, Phys. Rev. D 17 (1978) 3247–3256
In S-duality and relation to t Hoofts operators
- Anton Kapustin, Edward Witten, Electric-Magnetic Duality And The Geometric Langlands Program, Communications in Number Theory and Physics Volume 1 (2007) Number 1 (arXiv:hep-th/0604151)
Last revised on June 11, 2023 at 18:13:07. See the history of this page for a list of all contributions to it.