nLab holographic entanglement entropy
Context
Quantum systems
-
quantum algorithms:
Measure and probability theory
Measure theory
Probability theory
Information geometry
Thermodynamics
Theorems
Applications
Contents
Idea
The term holographic entanglement entropy refers to expressions of entanglement entropy in boundary quantum field theories, via a version of AdS-CFT duality (“holography”), in terms of the geometry of a higher-dimensional bulk spacetime.
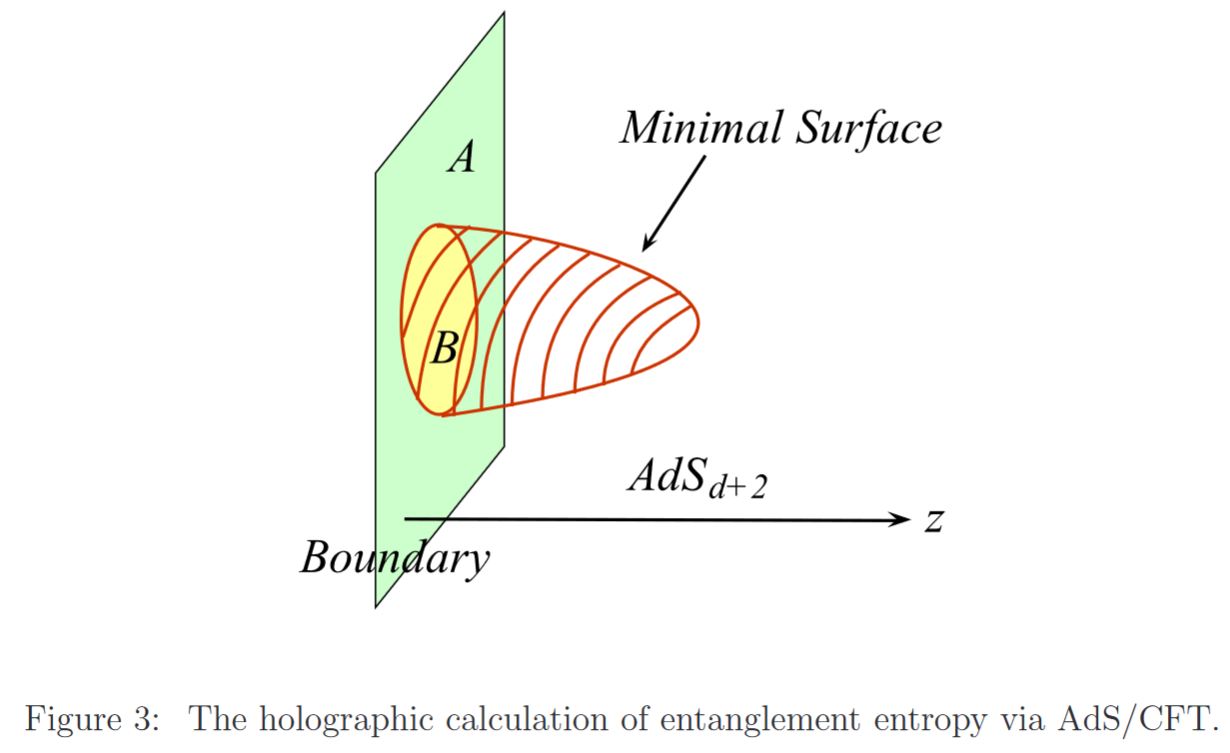
The essential idea is that the entanglement entropy of a region in the domain of a boundary field theory should be proportional to the volume (length, area, …) of the hypersurface in the bulk spacetime which shares the same boundary and which has minimal volume with this property. A more precise version of this idea is given by the Ryu-Takayanagi formula, see below.
This kind of relation between entropy of quantum systems and area/volumes of critical surfaces in a curved spacetime is akin to the Bekenstein-Hawking entropy-formula for black holes, and indeed it is meant to subsume the black hole entropy-formula for black holes in anti de Sitter spacetimes.
While in the original context of the AdS-CFT correspondence the Ryu-Takayanagi formula remains ill-defined, or at least intractable in detail (not the least because it is, ultimately, a statement about non-perturbative string theory, hence about M-theory, which remains elusive), its general idea led to the discovery of fully well-defined discretized (“toy”) models of holography in terms of tensor networks that express (code subspaces) of quantum error correcting codes (such as the HaPPY code and Majorana dimer codes). In these holographic tensor network models the behaviour of holographic entanglement entropy, and of several other expected aspects of holography, turn out to have a faithful reflection (up to lattice effects caused by the discretization) amenable to explicit analysis, by tools
-
from condensed matter physics (see also at AdS/CMT).
The power of these quantum information theory-methods in making precise and detailed sense of quantum gravity in a holographic bulk spacetime has re-inforced the earlier idea in AdS/CFT that notions of spacetime and of quantum gravity may be holographically defined and in fact emerge from non-gravitational quantum physics, and here specifically from quantum entanglement – an idea that has become known under the slogan “It from Qbit” (see also Georgescu 19). Just to keep in mind that, a priori, this applies “only” to the extra (higher) bulk dimensions of spacetime, while the definition of the boundary field theory typically relies on some notion domain space(-time) already (maybe unless one considers bulk duals of D(-1)-branes…).
Ryu-Takayanagi formula
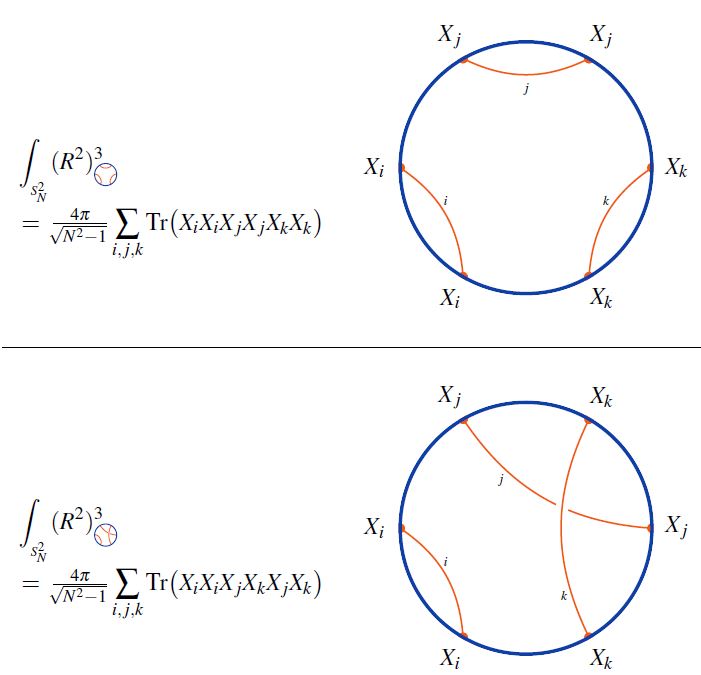
For quantum field theories that are exhibited as boundary field theories on the asymptotic boundary of an approximately anti de Sitter spacetime via some approximation to AdS-CFT duality (for instance for QCD via AdS-QCD duality) their entanglement entropy of a given bounded domain turns out to be proportional to the volume (area) of the minimal-area codimension-2 hypersurface inside the bulk spacetime that has the same boundary (see Nishioka-Ryu-Takayanagi 09 (3.3) for review of the formula and Lewkowycz-Maldacena 13 for a conceptual explanation).
graphics grabbed from Nishioka-Ryu-Takayanagi 09
This relation is known as the Ryu-Takayanagi formula (Ryu-Takayanagi 06a, Ryu-Takayanagi 06b) for holographic computation of entanglement entropy, or holographic entanglement entropy, for short.
This is a generalization of the proportionality of black hole entropy to the area of its event horizon. Indeed, AdS-CFT duality applies to the near horizon geometry of black branes, the higher-dimensional generalizations of black holes and reduces 4d black holes under suitable KK-compactification (see also at black holes in string theory)
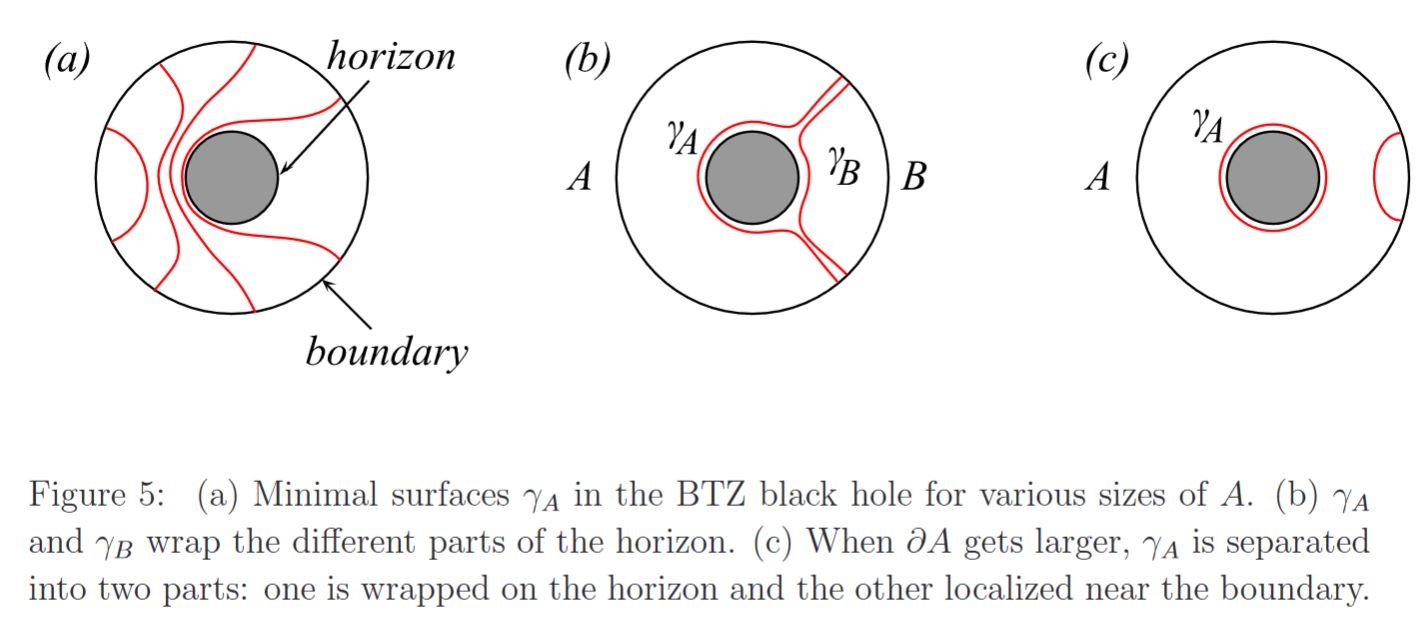
graphics grabbed from Nishioka-Ryu-Takayanagi 09
In fact quantum corrections to the black hole entropy in the presence of matter fields is equal to the entanglement entropy. (Ryu-Takayanagi 06a, p. 13)
Various properties of entanglement entropy find immediate geometric interpretations this way, for instance subadditivity

graphics grabbed from Nishioka-Ryu-Takayanagi 09
Tensor network models
Further discussion of implications of the Ryu-Takayanagi formula in van Raamsdonk 10 suggested that the logic may also be turned around: Instead of computing entanglement entropy of a given boundary field theory from known bulk geometry, conversely the bulk spacetime may be reconstructed from knowledge of the entanglement entropy of a boundary field theory.
Talking this perspective to the extreme suggests a description of bulk spacetimes entirely in terms of quantum information theory/entanglement-relations of a boundary QFT (“tensor networks”, Swingle 09, Swingle 12, and quantum error correction codes ADH 14, PYHP 15, HNQTWY 16, see Harlow 18, Jahn-Eisert 21 for review).
Here a tensor network Poincaré dual to a finite-stage hyperbolic tesselation of the hyperbolic plane is interpreted as a discretized model for a bulk spacetime with holographic quantum state on its asymptotic boundary being given by the string diagram-evaluation of the tensor network as a linear map to the tensor product of spaces corresonding to the edges crossing the boundary of the tesselation.
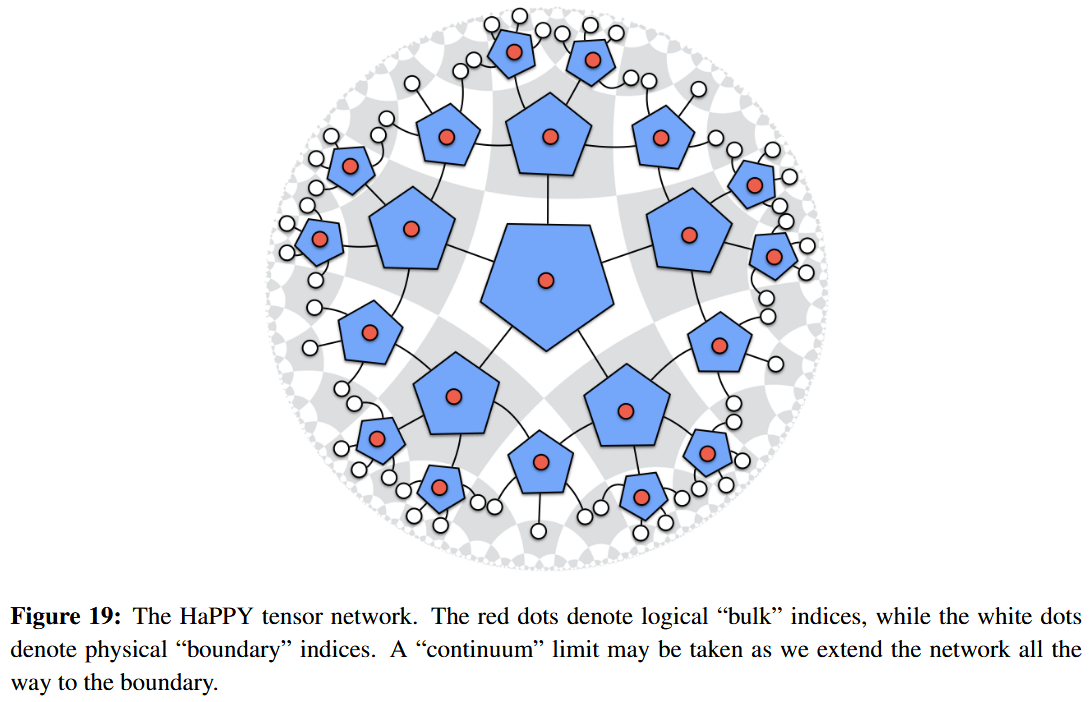
One shows (ADH 14) that this is a decent (“toy”) model of expected properties of bulk/boundary holography if this tensor network gives the code subspace of a quantum error correcting code.
For example, the tensor network corresponding to the pentagonal tesselation with a perfect tensor of rank assigned to each tile yields a quantum error correcting code now known as the HaPPY code.
The idea is that the code subspace of this HaPPY code is that subspace of the boundary space of quantum states which holographically corresponds to all bulk states without a black hole in the bulk.

More generally, deleting any of the tiles in the interior of the tesselation is interpreted as the appearance of a bulk black hole, whose Bekenstein-Hawking entropy is carried by the quantum states carried by the loose edges that cross over the “event horizon” to the now deleted tiles.
The extreme case that all tiles are deleted from the tensor network, is thus interpreted describing a black hole that has swallowed up the entire bulk spacetime such that its horizon now coincides with the previous asymptotic boundary, whence its quantum states and entropy now coincide with that of the holographic boundary theory.
In this discrete HaPPY code model for the AdS-CFT correspondence the Ryu-Takayanagi formula for holographic entanglement entropy (above) has an exact proof PYHP 15, Theorem 2.
Chord diagram representation
In fact, holographic entanglement entropy in the HaPPY code turns out to be entirely encoded by the dimer network in the underlying Majorana dimer code (JGPE 19):
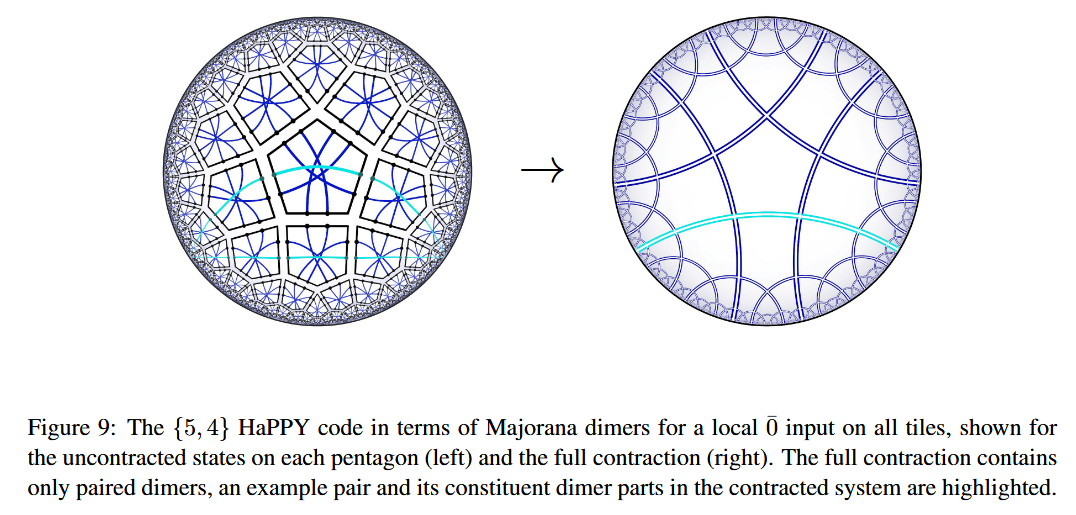
in that the entanglement entropy of any Majorana dimer code-tensor network state turns out to count the number of dimers that cross between the (connected) subregion and its complement:
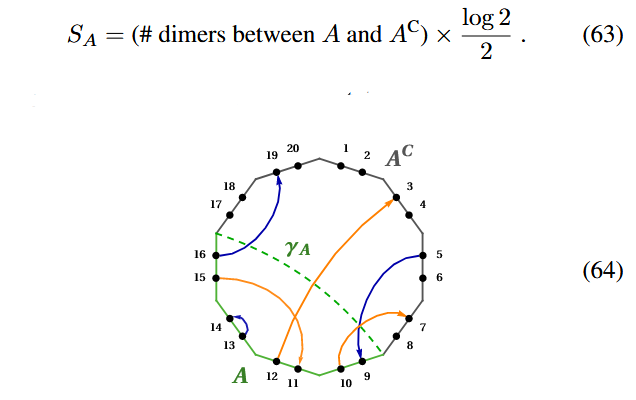
In the case that the dimers correspond to the hyperbolic tesselation from the HaPPY code, this entropy formula
recovers the Ryu-Takayanagi formula (JGPE 19 (78)), as here the number of chords crossing any hyperbolic geodesic grows linearly with the length of this geodesic.
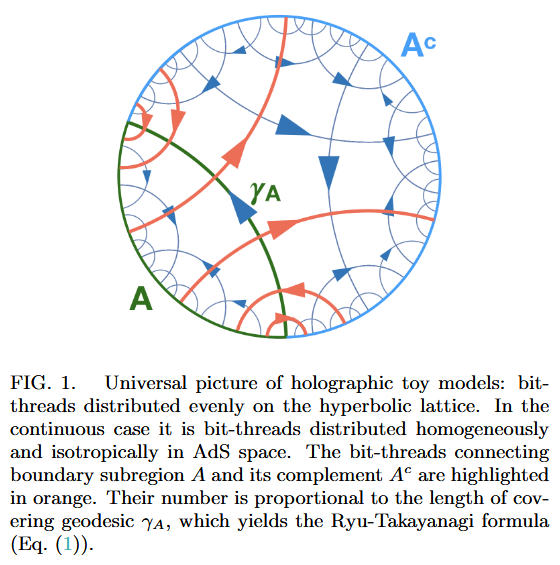
In the continuum limit this says that holographic entanglement entropy is exhibited by the geodesic flow out of the given subregion through its corresponding minimal bulk surface, an idea that was previously proposed in “bit-thread models” for holographic entanglement entropy (Freedman & Headrick 16):

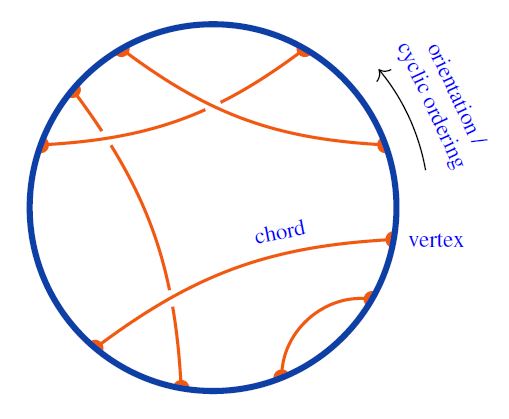
Following Sati-Schreiber 19c we recognize the above Majorana dimer/bit-thread networks from JGPE 19, Yan 19 as chord diagram-encodings of holographic bulks (p. 38).
Notice how each chord here reflects at the same time
-
one entangled pair of qbits in the boundary quantum system;
-
a geodesic through the hyperbolic plane bulk spacetime.
This is a (rigorous) state of affairs reminiscent of the “ER = EPR” slogan.
Related concepts
-
gravitational entropy
References
General
The original articles are
-
Shinsei Ryu, Tadashi Takayanagi, Holographic Derivation of Entanglement Entropy from AdS/CFT, Phys. Rev. Lett. 96:181602, 2006 (arXiv:hep-th/0603001)
-
Shinsei Ryu, Tadashi Takayanagi, Aspects of Holographic Entanglement Entropy, JHEP 0608:045, 2006 (arXiv:hep-th/0605073)
A proposal for a conceptual explanation:
-
Aitor Lewkowycz, Juan Maldacena, Generalized gravitational entropy, J. High Energ. Phys. (2013) 2013: 90 (arXiv:1304.4926)
-
Nele Callebaut, Entanglement in conformal field theory and holography [arXiv:2303.16827]
Review:
-
Jens Eisert, M. Cramer, M.B. Plenio, Area laws for the entanglement entropy - a review, Rev. Mod. Phys. 82, 277 (2010) (arXiv:0808.3773)
-
Tatsuma Nishioka, Shinsei Ryu, Tadashi Takayanagi, Holographic Entanglement Entropy: An Overview, J. Phys. A 42 504008 (2009) [arXiv:0905.0932, doi:10.1088/1751-8113/42/50/504008]
-
Matthew Headrick, Lectures on entanglement entropy in field theory and holography (arXiv:1907.08126)
-
Bei Zeng, Xie Chen, Duan-Lu Zhou, Xiao-Gang Wen:
Sec. 5 of: Quantum Information Meets Quantum Matter – From Quantum Entanglement to Topological Phases of Many-Body Systems, Quantum Science and Technology (QST), Springer (2019) arXiv:1508.02595, doi:10.1007/978-1-4939-9084-9
-
Bin Chen, Holographic Entanglement Entropy: A Topical Review, Communications in Theoretical Physics, 71 (2019) 837 [doi:10.1088/0253-6102/71/7/837]
-
Bowen Chen, Bartlomiej Czech, Zi-zhi Wang, Quantum Information in Holographic Duality, Rept. Prog. Phys. 85 (2022) 4, 046001 [arXiv:2108.09188, doi:10.1088/1361-6633/ac51b5]
-
Edward Witten section 9 of: Introduction to Black Hole Thermodynamics [arXiv:2412.16795]
Textbook account:
- Mukund Rangamani, Tadashi Takayanagi, Holographic Entanglement Entropy, Lecture Notes in Physics 931, Springer (2017) [doi:10.1007/978-3-319-52573-0, arXiv:1609.01287]
Survey talks:
-
Robert Myers, Holographic entanglement entropy, (pdf slides)
-
Shinsei Ryu, Holographic geometry in Entanglement Renormalization (pdf slides)
-
Juan Jottar, (Entanglement) Entropy in three-dimensional higher spin theories (pdf slides)
-
Matthew Headrick, Entanglement entropies in holographic field theory (pdf slides)
-
Tom Hartmann, Entanglement entropy and geometry, talk slides, 2014 (pdf)
An influential argument that this relation implies that entanglement in the boundary theory is what makes spacetime as such appear in the bulk theory is due to
-
Mark Van Raamsdonk, Building up spacetime with quantum entanglement, Gen. Rel. Grav. 42 (2010) 2323-2329; Int. J. Mod. Phys. D19 (2010) 2429-2435 (arXiv:1005.3035)
-
Mark Van Raamsdonk, Building up spacetime with quantum entanglement II: It from BC-bit (arXiv:1809.01197)
reviewed in
- Mark Van Raamsdonk, Lectures on Gravity and Entanglement, chapter 5 in New Frontiers in Fields and Strings
TASI 2015 Proceedings of the 2015 Theoretical Advanced Study Institute in Elementary Particle Physics 2015 Theoretical Advanced Study Institute in Elementary Particle Physics (arXiv:1609.00026)
Discussion of the corresponding continuum theory, formulated via local nets of observables in algebraic quantum field theory:
-
Edward Witten, Notes on Some Entanglement Properties of Quantum Field Theory, Rev. Mod. Phys. 90, 45003 (2018) (arXiv:1803.04993)
-
Thomas Faulkner, The holographic map as a conditional expectation (arXiv:2008.04810)
See also:
-
Matthew Headrick, Veronika E. Hubeny, Covariant bit threads [arXiv:2208.10507]
-
Eugenia Colafranceschi, Xi Dong, Donald Marolf, Zhencheng Wang, Algebras and Hilbert spaces from gravitational path integrals: Understanding Ryu-Takayanagi/HRT as entropy without invoking holography [arXiv:2310.02189]
Via holographic tensor networks and quantum codes
Relation to renormalization of entanglement and tensor networks is due to
-
Brian Swingle, Entanglement Renormalization and Holography, Phys. Rev. D 86, 065007 (2012) (arXiv:0905.1317)
-
Brian Swingle, Constructing holographic spacetimes using entanglement renormalization (arXiv:1209.3304, spire:1185813)
and further in terms of quantum error correcting codes due to
-
Ahmed Almheiri, Xi Dong, Daniel Harlow, Bulk Locality and Quantum Error Correction in AdS/CFT, JHEP 1504:163,2015 (arXiv:1411.7041)
-
Fernando Pastawski, Beni Yoshida, Daniel Harlow, John Preskill, Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence, JHEP 06 (2015) 149 (arXiv:1503.06237)
-
Patrick Hayden, Sepehr Nezami, Xiao-Liang Qi, Nathaniel Thomas, Michael Walter, Zhao Yang, Holographic duality from random tensor networks, JHEP 11 (2016) 009 (arXiv:1601.01694)
-
Daniel Harlow, The Ryu–Takayanagi Formula from Quantum Error Correction, Comm. Math. Phys. 354 (2017) 865–912 [doi:10.1007/s00220-017-2904-z, arXiv:1607.03901]
-
Helia Kamal, Geoffrey Penington, The Ryu-Takayanagi Formula from Quantum Error Correction: An Algebraic Treatment of the Boundary CFT (arXiv:1912.02240)
reviewed in
-
John Preskill, Is spacetime a quantum error-correcting code?, talk at KITP 2015 (pdf, pdf)
-
Daniel Harlow, TASI Lectures on the Emergence of Bulk Physics in AdS/CFT (arXiv:1802.01040)
-
Pratik Rath, Aspects of Holography And Quantum Error Correction, 2020 (pdf, pdf)
-
Daniel Harlow, Computation and Holography, talk at Snowmass Computational Frontier Workshop 2020 (pdf, pdf)
-
Tanay Kibe, Prabha Mandayam, Ayan Mukhopadhyay, Holographic spacetime, black holes and quantum error correcting codes: A review (arXiv:2110.14669)
See also
- Ahmed Almheiri, Holographic Quantum Error Correction and the Projected Black Hole Interior (arXiv:1810.02055)
Further development of these tensor networks:
-
Tamara Kohler, Toby Cubitt, Toy Models of Holographic Duality between local Hamiltonians, J. High Energy Phys. 2019:17 (2019) (arXiv:1810.08992)
-
Ning Bao, Geoffrey Penington, Jonathan Sorce, Aron C. Wall, Beyond Toy Models: Distilling Tensor Networks in Full AdS/CFT, JHEP 2019:69 (arXiv:1812.01171)
-
Ning Bao, Geoffrey Penington, Jonathan Sorce, Aron C. Wall, Holographic Tensor Networks in Full AdS/CFT (arXiv:1902.10157)
-
Matthew Steinberg, Sebastian Feld, Alexander Jahn, Holographic Codes from Hyperinvariant Tensor Networks [arXiv:2304.02732]
The bit-thread proposal for associating holographic entanglement entropy with geodesic flow in hyperbolic space:
- Michael Freedman, Matthew Headrick, Bit threads and holographic entanglement, Comm. Math. Phys. 352, 407 (2017) (arXiv:1604.00354)
Embedding of the HaPPY code and the bit-thread models in more general Majorana dimer codes:
-
Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting codes, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
-
Alexander Jahn, Zoltán Zimborás, Jens Eisert, Central charges of aperiodic holographic tensor network models, Phys. Rev. A 102, 042407 (arXiv:1911.03485)
reviewed in:
-
Alexander Jahn, Jens Eisert, Holographic tensor network models and quantum error correction: A topical review, Quantum Sci. Technol. 6 033002 (arXiv:2102.02619, doi:10.1088/2058-9565/ac0293)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)
See also:
-
Felix M. Haehl, Eric Mintun, Jason Pollack, Antony J. Speranza, Mark Van Raamsdonk, Nonlocal multi-trace sources and bulk entanglement in holographic conformal field theories, J. High Energ. Phys. (2019) 2019: 005 (arxiv:1904.01584, talk recording)
-
Han Yan, Hyperbolic Fracton Model, Subsystem Symmetry, and Holography, Phys. Rev. B 99, 155126 (2019) (arxiv:1807.05942)
-
Chris Akers, Geoff Penington, Quantum minimal surfaces from quantum error correction (arXiv:2109.14618)
-
Alexander Jahn, Marek Gluza, Charlotte Verhoeven, Sukhbinder Singh, Jens Eisert. Boundary theories of critical matchgate tensor networks (arXiv:2110.02972)
-
Pablo Basteiro, Giuseppe Di Giulio, Johanna Erdmenger, Jonathan Karl, René Meyer, Zhuo-Yu Xian, Towards Explicit Discrete Holography: Aperiodic Spin Chains from Hyperbolic Tilings arXiv:2205.05693
-
Lucas Daguerre, Matias Ginzburg, Gonzalo Torroba, Holographic entanglement entropy inequalities beyond strong subadditivity [arXiv:2208.03334]
-
Scott Aaronson, Jason Pollack, Discrete Bulk Reconstruction [arXiv:2210.15601]
Computation of black hole entropy in 4d via AdS4-CFT3 duality from holographic entanglement entropy in the ABJM theory for the M2-brane is discussed in
- Jun Nian, Xinyu Zhang, Entanglement Entropy of ABJM Theory and Entropy of Topological Black Hole (arXiv:1705.01896)
Discussion in terms of DHR superselection theory:
- Horacio Casini, Marina Huerta, Javier M. Magan, Diego Pontello, Entanglement entropy and superselection sectors I. Global symmetries (arXiv:1905.10487)
Discussion of gauge symmetry of holographic tensor networks and their quantum error correcting codes:
- Kfir Dolev, Vladimir Calvera, Sam Cree, Dominic J. Williamson, Gauging the bulk: generalized gauging maps and holographic codes (arXiv:2108.11402)
In relation to renormalization group flow:
- Keiichiro Furuya, Nima Lashkari, Mudassir Moosa, Renormalization group and approximate error correction (arXiv:2112.05099)
Musings on possible implications on relations between quantum gravity and quantum information (specifically quantum entanglement):
-
Brian Swingle: Spacetime from Entanglement, Annual Reviews 9 (2018) 345-358 [doi:10.1146/annurev-conmatphys-033117-054219]
-
Mark Van Raamsdonk: Spacetime from bits, Science 370 6513 (9 Oct 2020) 198-202 [doi:10.1126/science.aay9560]
-
Tadashi Takayanagi: Emergent Holographic Spacetime from Quantum Information [arXiv:2506.06595]
-
Simons Foundation, It from Qubit: Simons Collaboration on Quantum Fields, Gravity and Information
Final meeting: It from QBit 2023
-
Tom Banks, Holographic Space-time and Quantum Information [arXiv:2001.08205]
-
Iulia Georgescu: Strings and qubits, Nature Reviews Physics 1 (2019) 477 [doi:s42254-019-0087-6]
-
IAS Workshops on Quantum Information and Spacetime:
Wilson lines computing holographic entropy in
Discussion of BTZ black hole entropy and more generally of holographic entanglement entropy in 3d quantum gravity/AdS3/CFT2 via Wilson line observables in Chern-Simons theory:
-
Martin Ammon, Alejandra Castro, Nabil Iqbal, Wilson Lines and Entanglement Entropy in Higher Spin Gravity, JHEP 10 (2013) 110 (arXiv:1306.4338)
-
Jan de Boer, Juan I. Jottar, Entanglement Entropy and Higher Spin Holography in , JHEP 1404:089, 2014 (arXiv:1306.4347)
-
Alejandra Castro, Stephane Detournay, Nabil Iqbal, Eric Perlmutter, Holographic entanglement entropy and gravitational anomalies, JHEP 07 (2014) 114 (arXiv:1405.2792)
-
Mert Besken, Ashwin Hegde, Eliot Hijano, Per Kraus, Holographic conformal blocks from interacting Wilson lines, JHEP 08 (2016) 099 (arXiv:1603.07317)
-
Andreas Blommaert, Thomas G. Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Ashwin Dushyantha Hegde, Role of Wilson Lines in 3D Quantum Gravity, 2019 (spire:1763572)
-
Xing Huang, Chen-Te Ma, Hongfei Shu, Quantum Correction of the Wilson Line and Entanglement Entropy in the Chern-Simons Gravity Theory (arXiv:1911.03841)
-
Eric D'Hoker, Per Kraus, Gravitational Wilson lines in (arXiv:1912.02750)
-
Marc Henneaux, Wout Merbis, Arash Ranjbar, Asymptotic dynamics of gravity with two asymptotic regions (arXiv:1912.09465)
and similarly for 3d flat-space holography:
-
Arjun Bagchi, Rudranil Basu, Daniel Grumiller, Max Riegler, Entanglement entropy in Galilean conformal field theories and flat holography, Phys. Rev. Lett. 114, 111602 (2015) (arXiv 1410.4089)
-
Rudranil Basu, Max Riegler, Wilson Lines and Holographic Entanglement Entropy in Galilean Conformal Field Theories, Phys. Rev. D 93, 045003 (2016) (arXiv:1511.08662)
-
Wout Merbis, Max Riegler, Geometric actions and flat space holography (arXiv:1912.08207)
Discussion for 3d de Sitter spacetime:
- Alejandra Castro, Philippe Sabella-Garnier, Claire Zukowski, Gravitational Wilson Lines in 3D de Sitter (arXiv:2001.09998)
Application to AdS/QCD
Application to AdS/QCD:
- Zhibin Li, Kun Xu, Mei Huang, The entanglement properties of holographic QCD model with a critical end point (arXiv:2002.08650)
Entanglement island proposal for BH information paradox
Claims
Claim that the proper application of holographic entanglement entropy to the discussion of Bekenstein-Hawking entropy resolves the apparent black hole information paradox via the appearance of “entanglement islands”:
-
Geoff Penington, Stephen Shenker, Douglas Stanford, Zhenbin Yang, Replica wormholes and the black hole interior, J. High Energ. Phys. 2022 205 (2022) [doi:10.1007/JHEP05(2020)013, arXiv:1911.11977]
-
Ahmed Almheiri, Thomas Hartman, Juan Maldacena, Edgar Shaghoulian, Amirhossein Tajdini, Replica Wormholes and the Entropy of Hawking Radiation, J. High Energ. Phys. 2020 13 (2020) [doi:10.1007/JHEP05(2020)013, arXiv:1911.12333]
Review aimed at readers with minimal background:
- Ahmed Almheiri, Thomas Hartman, Juan Maldacena, Edgar Shaghoulian, Amirhossein Tajdini, The entropy of Hawking radiation, Rev. Mod. Phys. 93 35002 (2021) [doi:10.1103/RevModPhys.93.035002, arXiv:2006.06872]
See also:
- Suvrat Raju, Lessons from the Information Paradox [arXiv:2012.05770]
Criticism
Argument that the would-be proof of the island conjecture secretly works only for massive gravity:
-
Hao Geng, Andreas Karch, Massive Islands, J. High Energ. Phys. 2020 121 (2020) [doi:10.1007/JHEP09(2020)121, arXiv:2006.02438]
-
Hao Geng, Andreas Karch, Carlos Perez-Pardavila, Suvrat Raju, Lisa Randall, Marcos Riojas, Sanjit Shashi, Inconsistency of islands in theories with long-range gravity, J. High Energ. Phys. 2022 182 (2022) [doi:10.1007/JHEP01(2022)182]
-
Hao Geng, Graviton Mass and Entanglement Islands in Low Spacetime Dimensions [arXiv:2312.13336]
-
Hao Geng: Revisiting Recent Progress in the Karch-Randall Braneworld [arXiv:2306.15671]
reviewed in:
- Hao Geng, Recent Progress in Quantum Gravity: Karch-Randall Braneworld, Entanglement Islands and Graviton Mass, Washington (2022) [hdl:1773/49427]
and discussion of what to do about this problem:
- Hao Geng, Andreas Karch, Carlos Perez-Pardavila, Suvrat Raju, Lisa Randall, Marcos Riojas, Sanjit Shashi, Information Transfer with a Gravitating Bath, SciPost Phys. 10 103 (2021) [arXiv:2012.04671, doi:10.21468/SciPostPhys.10.5.103]
Claim that the whole argument relies on the false assumption that the split property holds for quantum gravity:
- Suvrat Raju, Failure of the split property in gravity and the information paradox, Classical and Quantum Gravity, 39 064002 [doi:10.1088/1361-6382/ac482b, arXiv:2110.05470]
Review in:
-
Nirmalya Kajuri, Of Islands, Holograms and Saving Quantum Physics From a Black Hole Paradox, Science – The Wire (Nov 2022)
a few sceptics have argued that while the calculations are correct, they don’t help resolve the black hole information-loss paradox. The troubles stem from the reservoir attached to the anti-de Sitter universe. The physicists who authored the island papers assumed that gravity stopped at the boundary of the anti-de Sitter space and didn’t enter the reservoir. This is not an innocuous assumption. […] The key takeaway is that the island way to recover information and save unitarity works perfectly well – if you slightly modify Einstein’s theory of gravity. These criticisms have been around for some two years now, and physicists are yet to resolve them in print. […] physicists continue to publish papers by the hundreds about the entanglement islands but few attempt to answer whether the islands are compatible with the Einsteinian gravity of our universe. […]
Claim of reconciliation of causal locality in the island proposal, under the explicit assumption of massive gravity:
- Hao Geng: The Mechanism behind the Information Encoding for Islands [arXiv:2502.08703]
See also:
-
Anna Karlsson, Concerns about the replica wormhole derivation of the island conjecture [arXiv:2101.05879]
-
Harvendra Singh: Islands and Icebergs contribute nothing to the Page curve (System with a symmetrical bath) [arXiv:2210.13970]
-
Saskia Demulder, Alessandra Gnecchi, Ioannis Lavdas, Dieter Lüst, Islands and Light Gravitons in type IIB String Theory [arXiv:2204.03669]
-
Emil Martinec: “Thus far, picturesque evocations of quantum wormholes remain largely just that – picturesque evocations.” (2nd Nov 2022)
Argument that discussion of the issue in the toy example of 2d JT gravity does not actually generalize to higher dimensions:
- Filip Landgren, Arvind Shekar, Islands and entanglement entropy in -dimensional curved backgrounds [arXiv:2401.01653]
Debate between a proponent and a critic :
- Islands and Black Hole Information ft. Suvrat Raju and Geoff Penington, podcast at Theoretically Podcasting (9 Mar 2024) [YT]
See also:
- Samir Mathur, podcast comment (2024) [x:1789623310348698044]
Reaction to the criticism:
- Stefano Antonini, Chang-Han Chen, Henry Maxfield, Geoff Penington: An apologia for islands [arXiv:2506.04311]
Chord diagrams and weight systems in Physics
The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:
-
In quantum many body models for for holographic brane/bulk correspondence:
For a unifying perspective (via Hypothesis H) and further pointers, see:
-
Hisham Sati, Urs Schreiber, Differential Cohomotopy implies intersecting brane observables, Adv. Theor. Math. Phys. 26 4 (2022) [doi:10.4310/ATMP.2022.v26.n4.a4arXiv:1912.10425]
-
David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states Lett. Math. Phys. 113 112 (2023) [arXiv:2105.02871, doi:10.1007/s11005-023-01725-4]
-
Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. 66 4 (2023) [doi:10.4153/S0008439523000206, arXiv:2210.05399]
Review:
- Carlo Collari, Weight systems which are quantum states, talk at QFT and Cobordism, CQTS (Mar 2023) web, pdf
In Chern-Simons theory
Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.
Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.
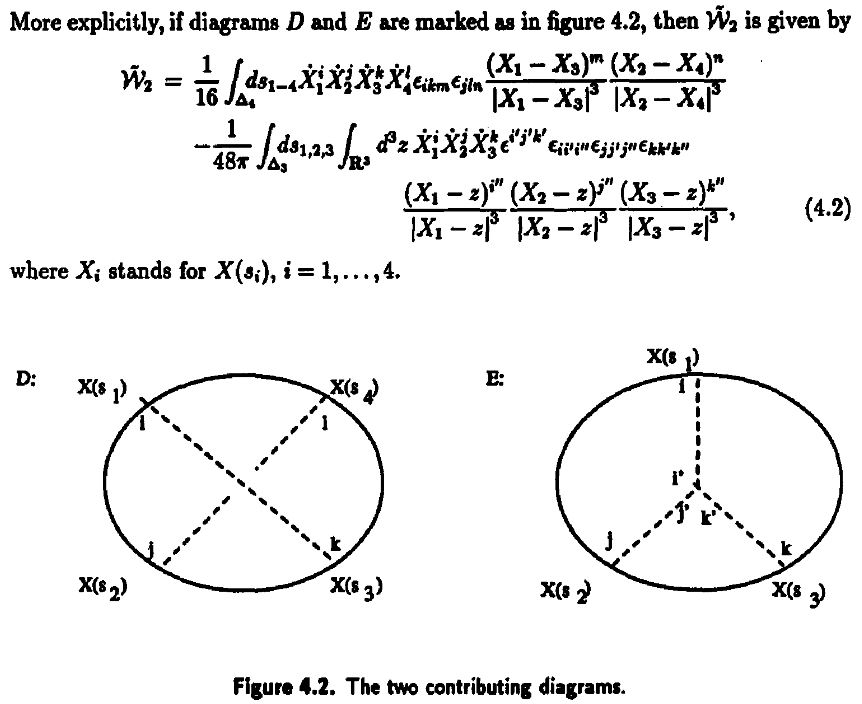
-
Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)
-
Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218)
Reviewed in:
- Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)
Applied to Gopakumar-Vafa duality:
- Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)
See also
-
Marcos Mariño, Chern-Simons theory, matrix integrals, and perturbative three-manifold invariants, Commun. Math. Phys. 253 (2004) 25-49 (arXiv:hep-th/0207096)
-
Stavros Garoufalidis, Marcos Mariño, On Chern-Simons matrix models (pdf, pdf)
For single trace operators in AdS/CFT duality
Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics
- Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
In , JT-gravity/SYK-model
Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on the holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
-
Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative , and chords in the double-scaled SYK model [arXiv:2212.13668]
-
Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]
-
Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]
and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
-
Henry W. Lin, The bulk Hilbert space of double scaled SYK, J. High Energ. Phys. 2022 60 (2022) arXiv:2208.07032, doi:10.1007/JHEP11(2022)060
-
Henry W. Lin, Douglas Stanford, A symmetry algebra in double-scaled SYK arXiv:2307.15725
-
Micha Berkooz, Ohad Mamroud: A Cordial Introduction to Double Scaled SYK [arXiv:2407.09396]
-
Adel A. Rahman, Leonard Susskind: -Chords, Wee-Chords, and de Sitter Space [arXiv:2407.12988]
In D/D-brane intersections
Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
As codes for holographic entanglement entropy

Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:
-
Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)

For Dyson-Schwinger equations
Discussion of round chord diagrams organizing Dyson-Schwinger equations:
-
Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)
-
Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)
-
Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]
Review in:
- Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)
Other
Appearance of horizontal chord diagrams in discussion of neutrino interactions in supernovae:
- Duff Neill, Hanqing Liu, Joshua Martin, Alessandro Roggero: Scattering Neutrinos, Spin Models, and Permutations [arXiv:2406.18677]
Last revised on June 13, 2025 at 07:45:11. See the history of this page for a list of all contributions to it.