nLab Polyakov gauge-string duality

Polyakov gauge/string duality

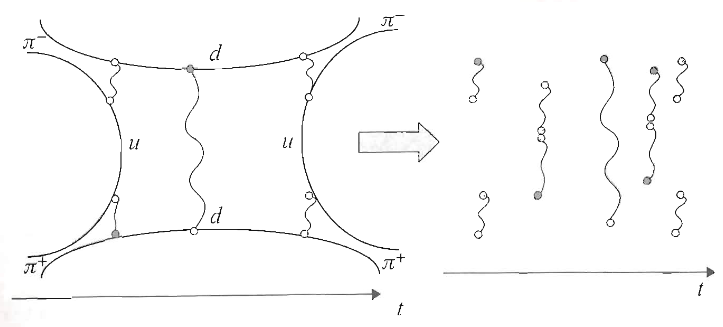
Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical reminiscences in Polyakov (2008)) under the name gauge/string duality, in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings.

The logic here proceeds in the following steps (cf. Polyakov (2007), §1 and see the commentary below):

(above graphics from Veneziano 2012, Fig 2.9)

1. flux tubes confine as dynamical strings

   The starting point is the hypothesis that the strong coupling of particles (such as quarks) by a (non-abelian) gauge field (such as the strong nuclear force) is embodied by the formation of “flux tubes” (“Wilson lines”) between pairs of such particles, which in themselves behave like strings with a given tension.

   $[$Kogut & Susskind (1974), (1975); Wilson (1974); Polyakov (1979), (1980), (1987); Makeenko & Migdal (1981), following Nambu (1970), Gotō (1971)]

   

   Under this assumption it would be:

   1. the flux tube/string‘s tension which keeps the particles at theirs endpoints together and hence confined,

   2. the fluctuations of these flux tubes/strings which follow Regge trajectories (such as of hadrons);

   3. the scattering of these flux tubes/strings which explains the observed Veneziano amplitudes,

   which are the main qualitative features to be explained.

   
   

   This picture is further concretified by the dual superconductor model of color confinement, where it is a background condensate of magnetic monopoles (revealed under DGC decomposition of the gluon field) which compresses the color flux lines to this flux tube/string, by a dual Meissner effect.

   
   

2. quantum flux tubes probe effective higher dimensions

   But if so, famous quantum effects make such flux tubes/strings behave like propagating in an effective/emergent higher-dimensional spacetime:

   • either because one regards the string as a priori propagating in non-critical spacetime-dimension $4$, in which case the dilaton field/Liouville field $\phi$ appears to cancel the quantum anomaly and acts like a warped 5th dimension:

   this was the point of view published in Polyakov (1981) but later claimed, in Polyakov (2008), to have originated already “by the end of ‘77”;

   • or because one regards the string as propagating in critical dimension (10 for the superstring) right away,

   which is the point of view adopted later in AdS-CFT duality, starting with Maldacena (1997)

   with only the endpoints of the flux tube/string constrained to lie in the original lower dimensional spacetime

   $[$Polyakov (1998), (1999)$]$

   which now appears (in modern language that Polyakov did not originally use) as a “brane” inside a higher dimensional bulk spacetime.

   Notice that in this picture the observable physics that we set out to describe takes place on the brane (underlying which is typically flat Minkowski spacetime!) at the asymptotic boundary of a higher-dimensional bulk spacetime, while the (potentially large) extra dimensions of a possibly $\sim$ AdS-bulk remain primarily unobservable. In fact, in Polyakov’s original picture the extra 5th dimension is not so much a spacetime dimension but a parameter for the thickness of the flux tube, which becomes non-vanishing due to quantum effects $[$cf. Polyakov (2008), p. 3$]$.

3. large/small $N$ confined gauge theory is holographic string theory/M-theory

   Thus the description of strongly coupled matter via flux tubes/strings now reveals a holographic situation where strongly-coupled quantum fields on intersecting branes are equivalently described by a theory of quantum gravity mediated by strings propagating in a higher dimensional bulk spacetime.

   In relation to gauge string duality this is due to Gubser, Klebanov & Polyakov (1998), which is now understood as part of AdS/CFT duality, but it is actually meant to be more general, cf. Polyakov & Rychkov (2000).

While this dual bulk string theory is itself strongly-coupled unless the “number of coincident branes” is humongous (the “large-N limit”) and thus unrealistic after all, the difference is that recognizing the branes as physical objects reveals a web of concrete hints as to the string’s strongly-coupled (non-perturbative) completion, going under the working title M-theory, cf. at AdS-CFT – Small $N$ corrections.

In summary, the plausible approach of understanding strongly-coupled quantum gauge theories by regarding their flux tubes as dynamical strings seems to recast the Millennium Problem of understanding strongly-coupled matter into the problem of formulating M-theory: Given M-theory, it ought to be possible to find intersecting brane models of single (or a small number of coincident) M-branes (such as the Witten-Sakai-Sugimoto model M5-brane system) on whose worldvolume the desired strongly-coupled field theory is realized (such as QCD).

Notice the decisive early insight of Alexander Polyakov here: While the idea that strings somehow describe hadronic bound states was the very origin of string theory in the early 1970s (“dual resonance models”), the mainstream abandoned this perspective in the later 1970s when the critical dimension and the full spectrum of the string became fully understood (cf. Goddard-Thorn no-ghost theorem) and declared that instead String theory should be understood as a grand unified theory of everything including quantum gravity (see e.g. the historical review of Veneziano (2012), esp. pp. 30-31 which still clings to this perspective). From here it was only through the long detour of first discovering, inside this grander theory: D-branes (and M5-branes) in the 1990s, then their near-horizon AdS-CFT duality just before the 2000s and then another decade of exploring intersecting D-brane models that the community in the 2010s came back full circle to Polyakov’s holographic perspective on QCD, now dubbed holographic QCD, in which strings are flux tubes that propagate not (alone) in the observable 4 spacetime dimensions but in a primarily unobservable (meanwhile known as Randall-Sundrum-like) higher-dimensional bulk spacetime – a holographic description of reality that Polyakov (1999) referred to as the wall of the cave, in allusion to Plato (cf. also Polyakov (2008), p. 6).

Our whereabouts in this remarkable picture are still often misunderstood today: If string theory is a theory of nature, then, it seems, we see the wall but not the cave: we live on a $\sim$Minkowskian brane intersection at the (asympotic) boundary of a primarily unobserved $\sim$anti de Sitter bulk – which may better be thought of not as physical space but as a configuration space of quantum flux.

References

Polyakov gauge/string duality

Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see notably also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical remarks in Polyakov (2008)) under the name gauge/string duality (cf. historical review in Polyakov (2008)), in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings:

Early suggestion that confined QCD is described by regarding the color-flux tubes as string-like dynamical degrees of freedoms:

• John Kogut, Leonard Susskind, Vacuum polarization and the absence of free quarks in four dimensions, Phys. Rev. D 9 (1974) 3501-3512 [doi:10.1103/PhysRevD.9.3501]

• Kenneth G. Wilson, Confinement of quarks, Phys. Rev. D 10 (1974) 2445 [doi:10.1103/PhysRevD.10.2445]

  (argument in lattice gauge theory)

• John Kogut, Leonard Susskind, Hamiltonian formulation of Wilson’s lattice gauge theories, Phys. Rev. D 11 (1975) 395 [doi:10.1103/PhysRevD.11.395]

  “The gauge-invariant configuration space consists of a collection of strings with quarks at their ends. The strings are lines of non-Abelian electric flux. In the strong coupling limit the dynamics is best described in terms of these strings. Quark confinement is a result of the inability to break a string without producing a pair. […]”

  “The confining mechanism is the appearance of one dimensional electric flux tubes which must link separated quarks. The appropriate description of the strongly coupled limit consists of a theory of interacting, propagating strings. […]”

  “This picture of the strongly coupled Yang-Mills theory in terms of a collection of stringlike flux lines is the central result of our analysis. It should be compared with the phenomenological use of stringlike degrees of freedom which has been widely used in describing hadrons.”

• Alexander Polyakov, String representations and hidden symmetries for gauge fields, Physics Letters B 82 2 (1979) 247-250 [doi:10.1016/0370-2693(79)90747-0]

• Alexander Polyakov, Gauge fields as rings of glue, Nuclear Physics B 164 (1980) 171-188 [doi:10.1016/0550-3213(80)90507-6]

  “The basic idea is that gauge fields can be considered as chiral fields, defined on the space of all possible contours (the loop space). The origin of the idea lies in the expectation that, in the confining phase of a gauge theory, closed strings should play the role of elementary excitations.”

• Yuri Makeenko, Alexander A. Migdal, Quantum chromodynamics as dynamics of loops, Nuclear Physics B 188 2 (1981) 269-316 [doi:10.1016/0550-3213(81)90258-3]

  “So the world sheet of string should be interpreted as the color magnetic dipole sheet. The string itself should be interpreted as the electric flux tube in the monopole plasma.”

• Alexander Polyakov, Gauge Fields and Strings, Routledge, Taylor and Francis (1987, 2021) [doi:10.1201/9780203755082, oapen:20.500.12657/50871]

$[$old personal page]: “My main interests this year [1993?] were directed towards string theory of quark confinement. The problem is to find the string Lagrangian for the Faraday’s ”lines of force“,which would reproduce perturbative corrections from the Yang-Mills theory to the Coulomb law at small distances and would give permanent confinement of quarks at large distances.”

Cf. also

• M. Lüscher: Symmetry-breaking aspects of the roughening transition in gauge theories, Nuclear Physics B 180 2 (1981) 317-329 [doi:10.1016/0550-3213(81)90423-5]

• Alexei Morozov, p. 6 of: String theory: what is it?, Sov. Phys. Usp. 35 (1992) 671-714 [doi:10.1070/PU1992v035n08ABEH002255]

Early suggestion, due to the Liouville field seen in the quantization of the bosonic string via the Polyakov action,

• Alexander Polyakov, Quantum geometry of bosonic strings, Phys. Lett. B 103 (1981) 207-210 [doi:10.1016/0370-2693(81)90743-7, pdf]

that such flux tubes regarded as confining strings are to be thought of a probing higher dimensional spacetime, exhibiting a holographic principle in which actual spacetime appears as a brane:

• Alexander Polyakov, String Theory and Quark Confinement, talk at Strings’97, Nucl. Phys. Proc. Suppl. 68 (1998) 1-8 [doi:10.1016/S0920-5632(98)00135-2, arXiv:hep-th/9711002]

  “In other words the open string flies in the $(x,\phi)$-space keeping its feet (its ends) on the ground $(\phi=0)$.”

• Alexander Polyakov, The wall of the cave, Int. J. Mod. Phys. A 14 (1999) 645-658 $[$arXiv:hep-th/9809057, doi:10.1142/S0217751X99000324$]$

  “We add new arguments that the Yang-Mills theories must be described by the non-critical strings in the five dimensional curved space. The physical meaning of the fifth dimension is that of the renormalization scale represented by the Liouville field.”

eventually culminating in the formulation of the dictionary for the AdS-CFT correspondence:

• Steven Gubser, Igor Klebanov, Alexander Polyakov, Gauge theory correlators from non-critical string theory, Physics Letters B 428 105-114 (1998) [doi:10.1016/S0370-2693(98)00377-3, hep-th/9802109]

“Relations between gauge fields and strings present an old, fascinating and unanswered question. The full answer to this question is of great importance for theoretical physics. It will provide us with a theory of quark confinement by explaining the dynamics of color-electric fluxes.”

• Alexander Polyakov, Vyacheslav Rychkov Gauge fields-strings duality and the loop equation, Nucl. Phys. B 581 (2000) 116-134 [doi:10.1016/S0550-3213(00)00183-8, arXiv:hep-th/0002106]

and the suggestion of finding the string-QCD correspondence:

• Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A 17 S1 (2002) 119-136 [doi:10.1142/S0217751X02013071, arXiv:hep-th/0110196]

“in the strong coupling limit of a lattice gauge theory the elementary excitations are represented by closed strings formed by the color-electric fluxes. In the presence of quarks these strings open up and end on the quarks, thus guaranteeing quark confinement. Moreover, in the $SU(N)$ gauge theory the strings interaction is weak at large $N$. This fact makes it reasonable to expect that also in the physically interesting continuous limit (not accessible by the strong coupling approximation) the best description of the theory should involve the flux lines (strings) and not fields, thus returning us from Maxwell to Faraday. In other words it is natural to expect an exact duality between gauge fields and strings. The challenge is to build a precise theory on the string side of this duality.”

Historical reminiscences:

• Alexander Polyakov, Confinement and Liberation, in Gerardus ’t Hooft (ed.) 50 Years of Yang-Mills Theory (2005) 311-329 [arXiv:hep-th/0407209, doi:10.1142/9789812567147_0013, doi:10.1142/5601]

“Already in 1974, in his famous large $N$ paper, ‘t Hooft already tried to find the string-gauge connections. His idea was that the lines of Feynman’s diagrams become dense in a certain sense and could be described as a 2d surface. This is, however, very different from the picture of strings as flux lines. Interestingly, even now people often don’t distinguish between these approaches. In fact, for the usual amplitudes Feynman’s diagrams don’t become dense and the flux lines picture is an appropriate one. However there are cases in which t’Hooft’s mechanism is really working.”

• Alexander M. Polyakov, §1 in: Beyond Space-Time, in The Quantum Structure of Space and Time, Proceedings of the 23rd Solvay Conference on Physics, World Scientific (2007) [arXiv:hep-th/0602011, pdf]

• Alexander M. Polyakov, From Quarks to Strings [arXiv:0812.0183]

  published as Quarks, strings and beyond, section 44 in: Paolo Di Vecchia et al. (ed.), The Birth of String Theory, Cambridge University Press (2012) 544-551 [doi:10.1017/CBO9780511977725.048]

  “By the end of ’77 it was clear to me that I needed a new strategy $[$for understanding confinement$]$ and I became convinced that the way to go was the gauge/string duality. […]” “Classically the string is infinitely thin and has only transverse oscillations. But when I quantized it there was a surprise – an extra, longitudinal mode, which appears due to the quantum ”thickening“ of the string. This new field is called the Liouville mode. […]”

  “I kept thinking about gauge/strings dualities. Soon after the Liouville mode was discovered it became clear to many people including myself that its natural interpretation is that random surfaces in 4d are described by the strings flying in 5d with the Liouville field playing the role of the fifth dimension. The precise meaning of this statement is that the wave function of the general string state depends on the four center of mass coordinates and also on the fifth, the Liouville one. In the case of minimal models this extra dimension is related to the matrix eigenvalues and the resulting space is flat.”

  “Since this 5d space must contain the flat 4d subspace in which the gauge theory resides, the natural ansatz for the metric is just the Friedman universe with a certain warp factor. This factor must be determined from the conditions of conformal symmetry on the world sheet. Its dependence on the Liouville mode must be related to the renormalization group flow. As a result we arrive at a fascinating picture – our 4d world is a projection of a more fundamental 5d string theory. […]”

  “At this point I was certain that I have found the right language for the gauge/string duality. I attended various conferences, telling people that it is possible to describe gauge theories by solving Einstein-like equations (coming from the conformal symmetry on the world sheet) in five dimensions. The impact of my talks was close to zero. That was not unusual and didn’t bother me much. What really caused me to delay the publication (Polyakov 1998) for a couple of years was my inability to derive the asymptotic freedom from my equations. At this point I should have noticed the paper of Klebanov 1997 in which he related D3 branes described by the supersymmetric Yang Mills theory to the same object described by supergravity. Unfortunately I wrongly thought that the paper is related to matrix theory and I was skeptical about this subject. As a result I have missed this paper which would provide me with a nice special case of my program. This special case was presented little later in full generality by Juan Maldacena (Maldacena 1997) and his work opened the flood gates.”

A detailed monograph:

• N. D. Hari Dass, Strings to Strings – Yang-Mills Flux Tubes, QCD Strings and Effective String Theories, Lecture Notes in Physics 1018, Springer (2024) [doi:10.1007/978-3-031-35358-1]

  Ch. 23:

  Effective String Theories (EST) of Yang-Mills Flux Tubes [doi:10.1007/978-3-031-35358-1_22, arXiv:2312.10629]

Discussion of corrections of flux tube-dynamics beyond the Nambu-Goto action:

• Michele Caselle, Nicodemo Magnoli, Alessandro Nada, Marco Panero, Dario Panfalone, Lorenzo Verzichelli: Confining strings in three-dimensional gauge theories beyond the Nambu–Gotō approximation, J. High Energ. Phys. 2024 198 (2024) [doi:10.1007/JHEP08(2024)198, arXiv:2407.10678]

• Michele Caselle, Nicodemo Magnoli, Alessandro Nada, Marco Panero, Dario Panfalone, Lorenzo Verzichelli: Effective String Theory of three-dimensional $SU(N)$ gauge theories beyond the Nambu–Gotō approximation [arXiv:2412.14204]

Dual superconductor model of confinement

General

Precursor discussion identifying the Polyakov dual flux tube strings as (akin to) vortices in a superconductor medium:

• Holger Bech Nielsen, Poul Olesen: Vortex-line models for dual strings, Nuclear Physics B 61 (1973) 45-61 [doi:10.1016/0550-3213(73)90350-7]

• Yoichiro Nambu: Strings, monopoles, and gauge fields, Phys. Rev. D 10 (1974) 4262 [doi:10.1103/PhysRevD.10.4262]

The articles now credited with (independently) proposing the dual superconductor model of color confinement:

• Stanley Mandelstam: Vortices and quark confinement in non-abelian gauge theories, Physics Letters B 53 5 (1975) 476–478 [doi:10.1016/0370-2693(75)90221-X]

• Gerard ’t Hooft; p 4-5 in: Gauge Fields with Unified Weak, Electromagnetic, and Strong Interactions, Rapporteur’s talk at E.P.S. International Conference on High Energy Physics, Palermo, Sicily (June 1975) [spire:2781, pdf, pdf]

• Gerard ’t Hooft: On the phase transition towards permanent quark confinement, Nuclear Physics B 138 1 (1978) 1–25 [doi:10.1016/0550-3213(78)90153-0]

Further discussion:

• Grigorios I. Poulis: Abelian dominance and adjoint sources in lattice QCD, Phys. Rev.D 54 (1996) 6974–6985 [doi:10.1103/PhysRevD.54.6974, arXiv:hep-lat/9601013]

• L. Del Debbio, M. Faber, Jeff Greensite, S. Olejnik: Some Cautionary Remarks on Abelian Projection and Abelian Dominance, Nucl. Phys. Proc. Suppl. 53 (1997) 141–147 [doi:10.1016/S0920-5632(96)00608-1, arXiv:hep-lat/9607053]

• Hiroko Ichie, Hideo Suganuma: Abelian dominance for confinement and random phase property of off-diagonal gluons in the maximally abelian gauge, Nuclear Physics B 548 1–-3 (1999) 365-382 [doi:10.1016/S0550-3213(99)00132-7, arXiv:hep-lat/9807025]

• John Ellis, N. E. Mavromatos: Confinement in Gauge Theories from the Condensation of World-Sheet Defects in Liouville String, Int . J. Mod. Phys. A 14 (1999) 3761–3788 [doi:10.1142/S0217751X99001743, arXiv:hep-th/9808172]

• Y. M. Cho, D. G. Pak: Magnetic Confinement in QCD, J. Korean Phys. Soc. 38 (2001) 151–154 [arXiv:hep-th/9906198]

• Y. M. Cho, D. G. Pak: Dynamical Symmetry Breaking and Magnetic Confinement in QCD [arXiv:hep-th/0006051]

• Y. M. Cho, D. G. Pak: Monopole condensation in $SU(2)$ QCD, Phys. Rev. D 65 (2002) 074027 [doi:10.1103/PhysRevD.65.074027, arXiv:hep-th/0201179]

• Kei-Ichi Kondo: Gauge-invariant gluon mass, infrared Abelian dominance and stability of magnetic vacuum, Phys. Rev. D 74 (2006) 125003 [doi:10.1103/PhysRevD.74.125003, arXiv:hep-th/0609166]

• Kei-Ichi Kondo, A. Shibata, T. Shinohara, S. Kato: Non-Abelian Dual Superconductor Picture for Quark Confinement, Phys. Rev. D 83 (2011) 114016 [doi:10.1103/PhysRevD.83.114016, arXiv:1007.2696]

• Y. M. Cho: Dimensional Transmutation by Monopole Condensation in QCD, Phys. Rev. D. 87 (2013) 085025 [doi:10.1103/PhysRevD.87.085025, arXiv:1206.6936]

• Y. M. Cho: Monopole Condensation and Mass Gap in $SU(3)$ QCD, International Journal of Modern Physics A 29 03n04 (2014) 1450013 [doi:10.1142/S0217751X14500134]

Review:

• Thomas Schaefer, Edward Shuryak; section III D of: Instantons in QCD, Rev. Mod. Phys. 70 (1998) 323–426 [doi:10.1103/RevModPhys.70.323, arXiv:hep-ph/9610451]

• Adriano Di Giacomo: Confinement of Color by Dual Superconductivity, Acta Physica Polonica B 28 12 (1997)

• Jeff Greensite: The Confinement Problem in Lattice Gauge Theory, Prog. Part. Nucl. Phys. 51 (2003) 1 [doi:10.1016/S0146-6410(03)90012-3, arXiv:hep-lat/0301023]

• Adriano Di Giacomo: Confinement of Color: Recent Progress [arXiv:hep-lat/0310021]

• Georges Ripka: Dual superconductor models of color confinement, Lecture Notes in Physics 639, Springer (2004) [doi:10.1007/b94800, arXiv:hep-ph/0310102]

• Adriano Di Giacomo: A Strategy to Study Confinement in QCD, Braz. J. Phys. 37 (2007) 208–213 [arXiv:hep-lat/0610027]

• Adriano Di Giacomo: Confinement by dual superconductivity: an update (2001) [pdf]

• Adriano Di Giacomo: The Dual Superconductor Picture for Confinement, in: Confinement, Duality, and Non-Perturbative Aspects of QCD, NATO Science Series: B 368, Springer (2002) 415–437 [doi:10.1007/0-306-47056-X_15]

• Kei-Ichi Kondo, Seikou Kato, Akihiro Shibata, Toru Shinohara: Quark confinement: Dual superconductor picture based on a non-Abelian Stokes theorem and reformulations of Yang–Mills theory, Physics Reports 579 (2015) 1–226 [doi:10.1016/j.physrep.2015.03.002]

  (emphasis on role of nonabelian Stokes theorem)

• Maxim Chernodub: QCD Vacuum as Dual Superconductor: Quark Confinement and Topology, Handbook of Nuclear Physics, Springer (2023) [doi:10.1007/978-981-19-6345-2_23]

See also:

• Tereza Mendes, Luis E. Oxman, Gustavo M. Simões, Rafael C. S. Tonhon: Cartan Fluxes in $SU(3)$ Lattice Gauge Theory [arXiv:2604.25003]

The DGC-decomposition

On decomposing, in a gauge invariant way, the gauge potential into an abelian background and nonabelian fluctuations:

The original articles:

• Yi-Shi Duan, Mo-Lin Ge: $SU(2)$ gauge theory and electrodynamics of $N$ moving magnetic monopoles, Scientia Sinica Mathematica 9 11 (1979) 1072–1081, reprinted in: Memorial Volume for Yi-Shi Duan, World Scientific (2018) 1-15 [doi:10.1142/9789813237278_0001]

• Y. M. Cho: Colored Monopoles, Phys. Rev. Lett. 44 (1980) 1115, Erratum Phys. Rev. Lett. 44 (1980) 1566 [doi:10.1103/PhysRevLett.44.1115]

• Faddeev & Niemi 1999

Further discussion:

• Sergei V. Shabanov: An effective action for monopoles and knot solitons in Yang-Mills theory, Phys. Lett. B 458 (1999) 322–330 [doi:10.1016/S0370-2693(99)00612-7, arXiv:hep-th/9903223]

• Bae, Cho & Kim 2002

• Michael L. Walker, Steven Duplij: Cho-Duan-Ge decomposition of QCD in the constraintless Clairaut-type formalism, Phys. Rev. D 91 064022 (2015) [doi:10.1103/PhysRevD.91.064022, arXiv:1411.6968]

• Kei-Ichi Kondo, T. Murakami, T. Shinohara: Yang-Mills theory constructed from Cho–Faddeev–Niemi decomposition, Prog. Theor. Phys. 115 (2006) 201–216 [doi:10.1143/PTP.115.201, arXiv:hep-th/0504107]

• Kei-Ichi Kondo, T. Murakami, T. Shinohara: BRST symmetry of $SU(2)$ Yang-Mills theory in Cho–Faddeev–Niemi decomposition, Eur. Phys. J.C 42 (2005) 475–481 [doi:10.1140/epjc/s2005-02344-4, arXiv:hep-th/0504198]

  (via BRST cohomology)

Review:

• KKSS 2015 §3

Relation to Faddeev-Skyrme model

Relation (for gauge group $SU(2)$, hence with coset space the 2-sphere $\S^2 \simeq SU(2)/SU(1)$) to the Fadeev-Skyrme model and Hopfion-like knot field configurations:

• Ludvig Faddeev, Antti J. Niemi: Partially Dual variables in $SU(2)$ Yang-Mills Theory, Phys. Rev. Lett. 82 (1999) 1624–1627 [doi:10.1103/PhysRevLett.82.1624, arXiv:hep-th/9807069]

• Shabanov 1999

• W. S. Bae, Y. M. Cho, Sang-Woo Kim: QCD versus Skyrme-Faddeev Theory, Phys. Rev. D 65 (2002) 025005 [doi:10.1103/PhysRevD.65.025005, arXiv:hep-th/0105163]

In lattice gauge theory

On the dual superconductor model of confinement in view of lattice QCD computations/simulations:

• Michael E. Peskin: Mandelstam ‘t Hooft Duality in Abelian Lattice Models, Annals Phys. 113 (1978) 122 [doi:10.1016/0003-4916(78)90252-X]

• Tsuneo Suzuki, Ichiro Yotsuyanagi: Possible evidence for Abelian dominance in quark confinement, Phys. Rev. D 42 (1990) 4257(R) [doi:10.1103/PhysRevD.42.4257]

• Paolo Cea, Leonardo Cosmai: Lattice investigation of dual superconductor mechanism of confinement, Nuclear Physics B - Proceedings Supplements 30 (1993) 572–575 [doi:10.1016/0920-5632(93)90276-C]

• Paolo Cea, Leonardo Cosmai: Dual Superconductor Mechanism of Confinement on the Lattice, Nuov Cim A 107 (1994) 541547 [doi:10.1007/BF02768788, arXiv:hep-lat/9210030]

• Paolo Cea, Leonardo Cosmai: The $SU(2)$ Confining Vacuum as a Dual Superconductor, Nucl. Phys. Proc. Suppl. 47 (1996) 318–321 [doi:10.1016/0920-5632(96)00065-5, arXiv:hep-lat/9509007]

• Hideo Suganuma, H. Ichie, K. Amemiya: Origin of Abelian Dominance in QCD in the Maximally Abelian Gauge, in: Quark Confinement and the Hadron Spectrum III, World Scientific (2000) 207–210 [doi:10.1142/9789812793713_0026]

• Hideo Suganuma, Naoyuki Sakumichi: Perfect Abelian dominance of confinement in quark-antiquark potential in $SU(3)$ lattice QCD [arXiv:1412.8489]

• Hideo Suganuma, Naoyuki Sakumichi: The three-quark potential and perfect Abelian dominance in $SU(3)$ lattice QCD, PoS LATTICE2015 (2016) 323 [arXiv:1511.05244 hep-lat]

• Paolo Cea, Leonardo Cosmai, Francesca Cuteri, Alessandro Papa: Flux tubes in the QCD vacuum, Phys. Rev. D 95 (2017) 114511 [doi:10.1103/PhysRevD.95.114511, arXiv:1702.06437 hep-lat]

• Hideo Suganuma, Naoyuki Sakumichi: Monopole Dominance of Confinement in $SU(3)$ Lattice QCD, PoS 336 267 (2018) [arXiv:1812.06827 hep-lat, pos:336/267, pdf]

• Zeinab Dehghan, Manfried Faber: What do we know about the confinement mechanism?, Phys. Part. Nuclei 56 (2025) 1148–1154 [doi:10.1134/S1063779625700236, arXiv:2412.10767 hep-lat]

In super-Yang-Mills theory

The dual superconductor model of confinement becomes analytically exact in $\mathcal{N}-2$ $D=4$ super Yang-Mills theory (cf. Seiberg-Witten theory) when broken to $\mathcal{N}=1$:

• Nathan Seiberg, Edward Witten: Monopole Condensation, And Confinement in $\mathcal{N}=2$ Supersymmetric Yang-Mills Theory, Nucl. Phys. B 426 (1994) 19–52 Erratum-ibid. B 430 (1994) 485-0486 [doi:10.1016/0550-3213(94)90124-4, arXiv:hep-th/9407087]

• Nathan Seiberg, Edward Witten: Monopoles, Duality and Chiral Symmetry Breaking in $\mathcal{N}=2$ Supersymmetric QCD, Nucl. Phys. B 431 (1994) 484–550 [doi:10.1016/0550-3213(94)90214-3, arXiv:hep-th/9408099]

Reviews with discussion of the impact on confinement in plain YM:

• Alexei Yung: What Do We Learn about Confinement from the Seiberg-Witten Theory, 3rd Moscow School of Physics and 28th ITEP Winter School of Physics [spire:527017,arXiv:hep-th/0005088]

• Michael Dine: On the Possibility of Demonstrating Confinement in Non-Supersymmetric Theories by Deforming Confining Supersymmetric Theories [arXiv:2211.17134]

In solid state physics

On experimentally accessible analogs of the dual superconductor model of confinement in solid state physics:

• M. Cristina Diamantini, Carlo A. Trugenberger, Valeri M. Vinokur: Confinement and Asymptotic Freedom with Cooper pairs, Nature Comm. Phys. 1 77 (2018) [doi:10.1038/s42005-018-0073-9, arXiv:1807.01984]

• M. Cristina Diamantini, Carlo A. Trugenberger: Superinsulators: a toy realization of QCD in condensed matter, Ch. 23 in Roman Jackiw – 80th Birthday Festschrift, World Scientific (2020) 275-286 [arXiv:2008.12541]

Review:

• Carlo A. Trugenberger: Superinsulators, Bose Metals and High-$T_c$ Superconductors: The Quantum Physics of Emergent Magnetic Monopoles, World Scientific (2022) [doi:10.1142/12688]

• Carlo A. Trugenberger: Superinsulation: Magnetic Monopoles and Electric Confinement in Condensed Matter, talk at CQTS (Feb 2025) [slides:pdf]

Via holographics QCD

Discussion of the dual superconductor model of color confinement via holographic QCD:

• Tsung-Sheng Huang, Wen-Yu Wen: Holographic Model of Dual Superconductor for Quark Confinement [arXiv:1607.08171]

• Antón F. Faedo, Carlos Hoyos, Javier G. Subils: Monopoles and confinement in three dimensions from holography, J. High Energ. Phys. 2023 218 (2023) [doi:10.1007/JHEP03(2023)218, arXiv:2212.04996]