nLab fundamental theorem of finitely generated abelian groups
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Contents
Statement
Theorem
(fundamental theorem of finitely generated abelian groups)
Every finitely generated abelian group is isomorphic to a direct sum of p-primary cyclic groups (for a prime number and a natural number ) and copies of the infinite cyclic group :
The summands of the form are also called the p-primary components of . Notice that the need not all be distinct.
fundamental theorem of finite abelian groups:
In particular every finite abelian group is of this form for , hence is a direct sum of cyclic groups.
fundamental theorem of cyclic groups:
In particular every cyclic group is a direct sum of cyclic groups of the form
where all the are distinct and is the maximal power of the prime factor in the prime decomposition of .
Specifically, for each natural number dividing it contains as the subgroup generated by . In fact the lattice of subgroups of is the formal dual of the lattice of natural numbers ordered by inclusion.
(e.g. Roman 12, theorem 13.4, Navarro 03)
This is a special case of the structure theorem for finitely generated modules over a principal ideal domain.
Examples
The following examples may be useful for illustrative or instructional purposes.
Example
For a prime number, there are, up to isomorphism, two abelian groups of order , namely
and
For the first is the Klein 4-group.
Example
For and two distinct prime numbers, , then there is, up to isomorphism, precisely one abelian group of order , namely
This is equivalently the cyclic group
The isomorphism is given by sending to .
Example
Moving up, for two distinct prime numbers and , there are exactly two abelian groups of order , namely and . The latter is the cyclic group of order . For instance, .
Example
Similarly, there are four abelian groups of order , three abelian groups of order , and so on.
More generally, theorem may be used to compute exactly how many abelian groups there are of any finite order (up to isomorphism): write down its prime factorization, and then for each prime power appearing therein, consider how many ways it can be written as a product of positive powers of . That is, each partition of yields an abelian group of order . Since the choices can be made independently for each , the numbers of such partitions for each are then multiplied.
Of all these abelian groups of order , of course, one of them is the cyclic group of order . The fundamental theorem of cyclic groups says it is the one that involves the one-element partitions , i.e. the cyclic groups of order for each .
Graphical representation
Remark
Theorem says that for any prime number , the p-primary part of any finitely generated abelian group is determined uniquely up to isomorphism by
-
a total number of powers of ;
-
a partition .
The corresponding p-primary group is
In the context of Adams spectral sequences it is conventional to depict this information graphically by
-
dots;
-
of which sequences of length are connected by vertical lines, for .
For example the graphical representation of the -primary group
is
This notation comes from the convention of drawing stable pages of multiplicative Adams spectral sequences and reading them as encoding the extension problem for computing the homotopy groups that the spectral sequence converges to:
-
a dot at the top of a vertical sequence of dots denotes the group ;
-
inductively, a dot vetically below a sequence of dots denotes a group extension of by the group represented by the sequence of dots above;
-
a vertical line between two dots means that the the generator of the group corresponding to the upper dot is, regarded after inclusion into the group extension, the product by of the generator of the group corresponding to the lower dot, regarded as represented by the generator of the group extension.
So for instance
stands for an abelian group which forms a group extension of the form
such that multiplication by takes the generator of the bottom copy of , regarded as represented by the generator of , to the generator of the image of the top copy of .
This means that of the two possible choices of extensions (by example ) corresponds to the non-trivial extension . Because then in
the image of the generator 1 of the first group in the middle group is .
Conversely, the notation
stands for an abelian group which forms a group extension of the form
such that multiplication by of the generator of the top group in the middle group does not yield the generator of the bottom group.
This means that of the two possible choices (by example ) corresponds to the trivial extension . Because then in
the generator 1 of the top group maps to the element in the middle group, and multiplication of that by is instead of , where the latter is the generator of the bottom group.
Similarly
is to be read as the result of appending to the previous case a dot below, so that this now indicates a group extension of the form
such that -times the generator of the bottom group, regarded as represented by the generator of the middle group, is the image of the generator of the top group. This is again the case for the unique non-trivial extension, and hence in this case the diagram stands for .
And so on.
For example the stable page of the -classical Adams spectral sequence for computation of the 2-primary part of the stable homotopy groups of spheres has in (“internal”) degree the following non-trivial entries:
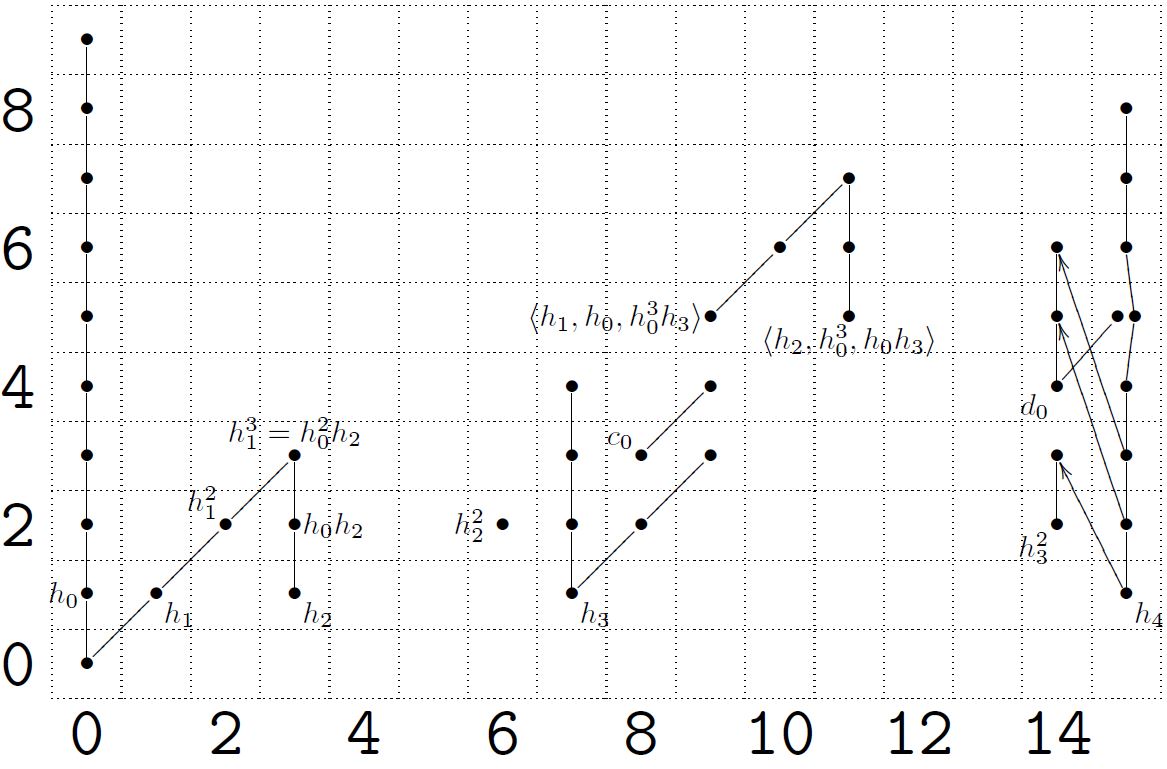
(graphics taken from (Schwede 12)))
Ignoring here the diagonal lines (which denote multiplication by the element that encodes the additional ring structure on which here we are not concerned with) and applying the above prescription, we read off for instance that (because all three dots are connected) while (because here the two dots are not connected). In total
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Here the only entry that needs further explanation is the one for . The symbol refers to the 2-adic integers, i.e. for the limit
This is not 2-primary, but it does arise when applying 2-completion of abelian groups to finitely generated abelian groups as in theorem . For more on this see at Adams spectral sequence – Convergence. Here we just note why this 2-completion is associated with the infinite sequence of dots
as in the above figure. Namely by the above prescrption, this infinite sequence should encode an abelian group such that it is an extension of by itself of the form
(Because it is supposed to encode an extension of by the group corresponding to the result of chopping off the lowest dot, which however in this case does not change the figure.)
Indeed, by this lemma we have a short exact sequence
Related concepts
References
Textbook accounts:
-
Steven Roman, Fundamentals of group theory, Birkhäuser (2012)
-
Joseph A. Gallian, Section 11 of: Contemporary Abstract Algebra, Chapman and Hall/CRC (2020) [doi:10.1201/9781003142331pdf]
A new proof of the fundamental theorem of finite abelian groups was given in
reviewed in
- John Sullivan: Classification of finite abelian groups lecture notes (2003) [pdf]
See also
Last revised on March 23, 2025 at 20:50:14. See the history of this page for a list of all contributions to it.