nLab knot sum

Definition

First, the connected sum $K_1 # K_2$ of boxed knots $K_1$ and $K_2$ is obtained by joining the boxes containing them.

(from Sossinsky 2023)

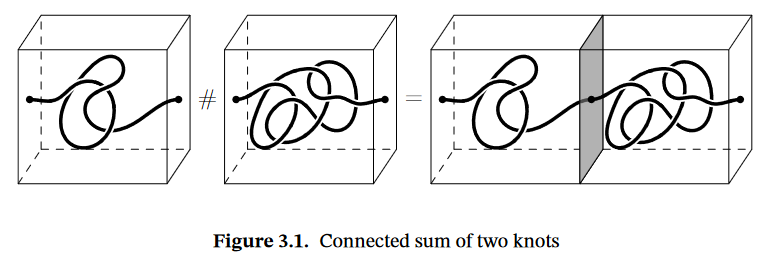
From this one obtains a notion of connected sum for ordinary (oriented) knots by observing that:

Proposition

There is a canonical bijection between the equivalence classes of boxed knots and the isotopy classes of oriented knots.

This bijection gives the connected sum of pairs of ordinary knots.

Properties

Theorem

The connected sum operation is associative and commutative:

• $K_1 # K_2 = K_2 # K_1$,

• $( K_1 # K_2 ) # K_3 = K_1 # ( K_2 # K_3 )$.

There are no inverse elements under the connected sum operation, i.e., $K # K' = \circ \implies K = K' = \circ$, where $\circ$ is the unknot.

Related concepts

• composite knot

• prime knot

References

• Alexei B. Sossinsky, §3 in: Knots, Links and Their Invariants: An Elementary Course in Contemporary Knot Theory, The Student Mathematical Library 101, AMS (2023) [doi:10.1090/stml/101]

Discussion in relation to Vassiliev knot invariants:

• Dror Bar-Natan, On the Vassiliev knot invariants, Topology 34 2 (1995) 423-472 [doi:10.1016/0040-9383(95)93237-2, pdf]