nLab octonion

Idea

The octonions or Cayley numbers (Cayley 1845) form a non-associative real star-algebra $\mathbb{O}$ similar to the complex numbers and the quaternions but with seven imaginary units adjoined.

The octonions arise from the quaternions in analogy – namely: by the Dickson double construction (Dickson 1919, (6)) – of how the quaternions arise from the complex numbers, and the complex numbers from the real numbers. These are precisely the normed division algebras over the real numbers, the octonions being the largest of the four. While the further Dickson double of the quaternions exists, called the sedenions, it is no longer a normed division algebra.

In continuation of how the complex numbers and quaternions control spin groups, real spin representations and supersymmetry up to dimension 7, the octonions control these up to the maximal dimension 11:

exceptional spinors and real normed division algebras

Lorentzian spacetime dimension	$\phantom{AA}$spin group	normed division algebra	$\,\,$ brane scan entry
$3 = 2+1$	$Spin(2,1) \simeq SL(2,\mathbb{R})$	$\phantom{A}$ $\mathbb{R}$ the real numbers	super 1-brane in 3d
$4 = 3+1$	$Spin(3,1) \simeq SL(2, \mathbb{C})$	$\phantom{A}$ $\mathbb{C}$ the complex numbers	super 2-brane in 4d
$6 = 5+1$	$Spin(5,1) \simeq$ SL(2,H)	$\phantom{A}$ $\mathbb{H}$ the quaternions	little string
$10 = 9+1$	Spin(9,1) ${\simeq}$ “SL(2,O)”	$\phantom{A}$ $\mathbb{O}$ the octonions	heterotic/type II string

For more on this see at supersymmetry and division algebras.

Generally, the algebra of octonions shows up, in one way or another, behind most, if not all, exceptional structures in group theory, Lie theory and differential geometry. See also at universal exceptionalism for more on this.

Definition

The following definition is in the style of Dickson 1919, Baez 02, second half of Section 2.2:

Definition

The octonions $\mathbb{O}$ are the elements of the non-associative star-algebra over the real numbers which is the Cayley-Dickson double of the star-algebra of quaternions $\mathbb{H}$ (with $\overline{(-)}$ denoting the conjugation-operation).

This means (see there) that if $i, j, k \in \mathbb{H}$ denote an orthonormal basis of imaginary unit-quaternions

graphics from SS21

$$\begin{aligned} & i^2 = j^2 = k^2 = -1 \\ & i j = k, \, j i = - k \;\;\;\text{and cyclic} \end{aligned}$$

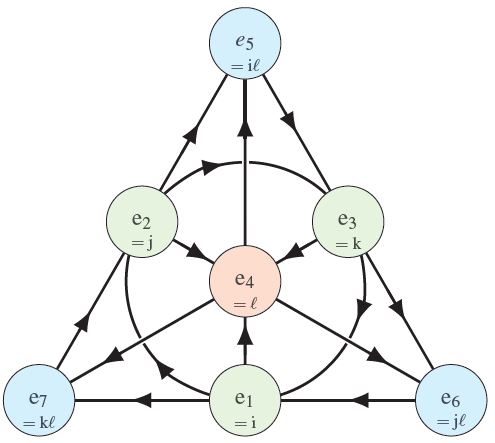
then the algebra $\mathbb{O}$ of octonions is generated from these $i, j , k$ and from one more element $\ell$, subject to these relations:

$$\begin{aligned} \ell^2 \;=\; -1 \,, \phantom{AAA} \overline{\ell} \;=\; - \ell \end{aligned}$$

and

$$\begin{aligned} q (\ell q') = \ell (\overline{q} q') \\ (q \ell) q' = (q \overline{q}') \ell \\ (\ell q) (q' \ell) = - \overline{q q'} \end{aligned}$$

for all quaternions $q_1, q_2 \in \mathbb{H}$.

This gives the multiplication table on the right, where any two consecutive arrows $a \to b \to c$ mean that $a b = c$, $c a = b$, $b c = a$ and $b a = -c$.

Example

The following computation shows the operation of consecutive left multiplication by the generators $\mathrm{e}_4$, $\mathrm{e}_5$, $\mathrm{e}_6$ $\mathrm{e}_7$ (according to Def. ) on any octonion $x = q + p \ell$ ($q,p \in \mathbb{H}$) is by reversal of the sign of the $\ell$-component, hence has as fixed linear subspace the quaternions (see HSS 18, Lemma 4.13 for application of this fact to M-branes):

$$\begin{aligned} \mathrm{e}_4 \Big( \mathrm{e}_5 \big( \mathrm{e}_6 (\mathrm{e}_7 x) \big) \Big) & = \ell \bigg( (i \ell) \Big( (j \ell) \big( (k \ell) x \big) \Big) \bigg) \\ & = \ell \bigg( (i \ell) \Big( (j \ell) \big( (k \overline{x}) \ell \big) \Big) \bigg) \\ & = \ell \Big( (i \ell) \big( (x k) j \big) \Big) \\ & = \ell \bigg( \Big( i \big( j (k \overline{x} \big) \Big) \ell \bigg) \\ & = \big( ( \underset{ \mathclap{ q + p \ell } }{ \underbrace{ x } } k) j \big) i \\ & = q k j i + \Big( \big( (q \ell) k \big) j \Big) i \\ & = q \underset{ = 1 }{ \underbrace{ k j i } } - (p \underset{ = 1 }{ \underbrace{ k j i } } ) \ell \\ & = q - p \ell \,. \end{aligned}$$

Of course the labels of the generators is not fixed. Here is another version:

Definition

The octonions $\mathbb{O}$ is the nonassociative algebra over the real numbers which is generated from seven generators $\{e_1, \cdots, e_7\}$ subject to the relations

1. for all $i$

   $e_i^2 = -1$

2. for $e_i \to e_j \to e_k$ an edge or circle in the following diagram (a labeled version of the Fano plane) the relations

   1. $e_i e_j = e_k$

   2. $e_j e_i = -e_k$

$\,$

This becomes a star-algebra with star involution

(1)$$\overline{(-)} \;\colon\; \mathbb{O} \longrightarrow \mathbb{O}$$

which is the antihomomorphism $\overline{a b} = \overline{b} \overline{a}$ that is given on the above generators by

$$\overline{e_i} \coloneqq - e_i \phantom{AAAA} i \in \{1, \cdots, 7\} \,.$$

Example

The product of all the generators with each other, bracketed to the right, is

$$e_7 (e_6 (e_5 (e_4 (e_3 ( e_2 (e_1 1 )))))) \;=\; + 1$$

Proof

By iteratively using the multiplication table in def. we compute as follows:

$$\begin{aligned} & e_7 (e_6 (e_5 (e_4 (e_3 (\underset{-e_4}{\underbrace{e_2 e_1}}))))) \\ & = - e_7 (e_6 (e_5 (e_4 (\underset{e_6}{\underbrace{e_3 e_4}})))) \\ & = - e_7 (e_6 (e_5 (\underset{e_3}{\underbrace{e_4 e_6}}))) \\ & = - e_7 (e_6 (\underset{-e_2}{\underbrace{e_5 e_3}})) \\ & = + e_7 (\underset{-e_7}{\underbrace{e_6 e_2}}) \\ & = - \underset{= -1}{\underbrace{e_7 e_7}} \\ & = + 1 \end{aligned}$$

Definition

(real and imaginary octonions)

As for the complex numbers one says that

• an imaginary octonion is an $a \in \mathbb{O}$ shuch that under the star involution (1) it is sent to its negative:

  $$\overline{a} = -a$$

• a real octonions is an $a \in \mathcal{O}$ shuch that under the star involution (1) it is sent to itself

  $$\overline{a} = a$$

Accordingly every octonion decomposes into a real part and an imaginary part:

$$Re(a) \coloneqq \tfrac{1}{2}(a + \overline{a}) \phantom{AA} Im(a) \coloneqq \tfrac{1}{2}(a - \overline{a}) \,.$$

Properties

General

Proposition

The octonions are not an associative algebra. But the non-zero octonions and the unit octonions form Moufang loops.

Proposition

(octonions are alternative)

The octonions form an alternative algebra

Proof

By linearity it is sufficient to check this on generators. So let $e_i \to e_j \to e_k$ be a circle or a cyclic permutation of an edge in the Fano plane as in Def. . Then by definition of the octonion multiplication we have

$$\begin{aligned} (e_i e_j) e_j &= e_k e_j \\ &= - e_j e_k \\ & = -e_i \\ & = e_i (e_j e_j) \end{aligned}$$

and similarly

$$\begin{aligned} (e_i e_i ) e_j &= - e_j \\ &= - e_k e_i \\ &= e_i e_k \\ &= e_i (e_i e_j) \end{aligned} \,.$$

Automorphisms

Proposition

The automorphism group of the octonions, as a real algebra, is the exceptional Lie group G₂.

See also at normed division algebra – automorphism

Left multiplication by imaginary octonions

Definition

Given any octonion $o$, then the operation of left multiplication by $o$

$$\array{ \mathbb{O} &\overset{L_o}{\longrightarrow}& \mathbb{O} \\ a &\mapsto& o a }$$

is an $\mathbb{R}-$linear map. Under composition of linear maps, this defines an associative monoid acting linearly on $\mathbb{O}$.

Proposition

(Clifford action of imaginary octonions)

Consider the Clifford algebra

$$Cl(Im(\mathbb{O}), -{\vert -\vert}^2)$$

on the underlying real vector space of that of the imaginary octonions (Def. ) regarded as an inner product space via the quadratic form given by the negative square norm.

Then the operation of left multiplication on $\mathbb{O}$ (def. ) induces a representation of this Clifford algebra on $\mathbb{R}^8 \simeq_{\mathbb{R}} \mathbb{O}$.

Proof

By alternativity (Prop. ) we have for every $v \in Im(\mathbb{O})$ and every $a \in \mathbb{O}$

$$\begin{aligned} L_v L_v (a) & \coloneqq v (v a) \\ & = (v v) a \\ & = - {\vert v\vert}^2 a \\ & = L_{- {\vert v\vert}^2} (a) \end{aligned}$$

Proposition

(consecutive left action by imaginary generators is unity)

The consecutive left multiplication action (Def. ) by all the imaginary octonion generators $e_i$ (Def. ) is $\pm$ the identity function on the octonions. Specifically, if one acts in increasing order of the labels in Def. , then it is +1:

$$L_{e_7} L_{e_6} L_{e_5} L_{e_4} L_{e_3} L_{e_2} L_{e_1} \;=\; + Id_{\mathbb{O}}$$

Proof

All the generators $e_i$ are imaginary octonions (Def. ). By Prop. their left action on $\mathbb{O}$ represents a Clifford algebra-action of $Cl(Im(\mathbb{O}), -{\vert-\vert}^2) \simeq Cl_{0,7}$ on $\mathbb{R}^{8} \simeq_{\mathbb{R}} \mathbb{O}$.

By the classification of real Clifford algebras, $Cl_{0,7}$ has, up to isomorphism, two different irreducible modules. Their underlying vector space is $\mathbb{R}^8$ in both cases, and so the left action of imaginary octonions we have must be one of the two. The two irreps may be distinguished by the action of the “volume element” $\Gamma_7 \Gamma_6 \cdots \Gamma_1$: On one of the two it acts as the identity, on the other as minus the identity.

Hence we may check the remaining sign by acting on any one octonion, for instance on the unit $1 \in \mathbb{O}$. Then the claim follows with the computation in Example :

$$\begin{aligned} L_{e_7} L_{e_6} L_{e_5} L_{e_4} L_{e_3} L_{e_2} L_{e_1} (1) & = e_7 (e_6 (e_5 (e_4 (e_3 ( e_2 (e_1 1 )))))) \\ & = + 1 \,. \end{aligned}$$

Basic triples

Definition

A special triple or basic triple is a triple $(e_1, e_2, e_3) \in \mathbb{O}^3$ of three octonions such that

• $e_i^2 = -1$

• $e_i e_j = - e_j e_i$ for $i \ne j$

• $e_i (e_j e_k) = - (e_j e_k) e_i$ for $i,j,k$ pairwise distinct.

(Whitehead 71, p. 691)

Remark

The choice of $e_1$ identifies an inclusion of the complex numbers $\mathbb{R} \hookrightarrow \mathbb{C} \hookrightarrow \mathbb{O}$.

Then the choice of $e_2$ on top of that identifies a compatible inclusion of the quaternions $\mathbb{R} \hookrightarrow \mathbb{C}\hookrightarrow \mathbb{H} \hookrightarrow \mathbb{O}$.

Finally the choice of $e_3$ on top of that induces a basis for all of $\mathbb{O}$.

Once we have given the octonions their natural inner product, an imaginary octonion squares to $-1$ iff it has norm $1$, and two imaginary octonions anticommute iff they are orthogonal. Thus we can equivalently define a basic triple to be an orthonormal triple of imaginary octonions such that the third is orthogonal to the subalgebra generated by the first two. (Given this, each is orthogonal to the subalgebra generated by the other two.)

Proposition

The set of basic triples, def. , forms a torsor over the automorphism group G₂ $= Aut(\mathbb{O})$.

(e.g. Baez 02, 4.1)

Relation to quaternions

Proposition

Let

$$\mathbb{H} = \langle 1, i, j, k\rangle$$

be the quaternions equipped with canonical basis elements, and let

(2)$$\mathbb{O} = \mathbb{H} \oplus \ell \mathbb{H}$$

be the octonions equipped with the linear basis induced by the Cayley-Dickson construction (via this def.).

Then the linear map

$$L_{\ell} L_{\ell i} L_{\ell j} L_{\ell k} \;\colon\; \mathbb{O} \longrightarrow \mathbb{O}$$

is an involution whose +1 eigenspace is $\ell \mathbb{H}$ and whose -1 eigenspace is $\mathbb{H}$, under the above identification (2).

(Here $L_{(-)}$ denotes the linear map on $\mathbb{O}$ given by left multiplication in $\mathbb{O}$.)

Proof

We use the Cayley-Dickson relations (this def.)

$$a (\ell b) = \ell (\overline{a} b) \,, \phantom{AA} a(\ell b) = (a \overline{b}) \ell \,, \phantom{AA} (\ell a) (b \ell^{-1}) = \overline{a b}$$

that hold in $\mathbb{O}$ for all $a,b \in \mathbb{H}$, as well as

$$\ell e = - e \ell$$

for all imaginary elements $e \in \mathbb{H}$.

With this we compute

$$\begin{aligned} & L_{\ell} L_{\ell i} L_{\ell j} L_{\ell k} ( a) \\ & = \ell( (\ell i) ( (\ell j) ( (\ell k) a ) ) ) \\ & = - \ell( (\ell i) ( (\ell j) ( (k \ell) a ) ) ) \\ & = - \ell( (\ell i) ( (\ell j) ( (k \overline{a}) \ell ) ) ) \\ & = + \ell( (\ell i) ( (\ell j) ( (k \overline{a}) \ell^{-1} ) ) ) \\ & = + \ell( (\ell i) ( \overline{j (k \overline{a})} ) ) \\ & = + \ell( (\ell i) ( \overline{i \overline{a}} ) ) \\ & = - \ell( (i \ell) ( \overline{i \overline{a}} ) ) \\ & = - \ell( ( i i \overline{a} ) \ell ) \\ & = + \ell( \overline{a} \ell ) \\ & = - \ell( \overline{a} \ell^{-1} ) \\ & = - a \end{aligned}$$

and

$$\begin{aligned} & L_{\ell} L_{\ell i} L_{\ell j} L_{\ell k} ( \ell a) \\ & = \ell( (\ell i) ( (\ell j) ( (\ell k) (\ell a) ) ) ) \\ & = \ell( (\ell i) ( (\ell j) ( (\ell k) ( \overline{a} \ell) ) ) ) \\ & = - \ell( (\ell i) ( (\ell j) ( \overline{k {\overline{a}}} ) ) ) \\ & = + \ell( (\ell i) ( (j \ell) ( \overline{k {\overline{a}}} ) ) ) \\ & = + \ell( (\ell i) ( (j k {\overline{a}}) \ell ) ) \\ & = - \ell( (\ell i) ( (j k {\overline{a}}) \ell^{-1} ) ) \\ & = - \ell( \overline{ i j k {\overline{a}} } ) \\ & = + \ell( \overline{ {\overline{a}} } ) \\ & = + \ell a \end{aligned}$$

Related concepts

• associative 3-form

• Fano plane

• Cayley plane

• octonionic Hopf fibration

• octonionic projective space

• split octonion

exceptional spinors and real normed division algebras

Lorentzian spacetime dimension	$\phantom{AA}$spin group	normed division algebra	$\,\,$ brane scan entry
$3 = 2+1$	$Spin(2,1) \simeq SL(2,\mathbb{R})$	$\phantom{A}$ $\mathbb{R}$ the real numbers	super 1-brane in 3d
$4 = 3+1$	$Spin(3,1) \simeq SL(2, \mathbb{C})$	$\phantom{A}$ $\mathbb{C}$ the complex numbers	super 2-brane in 4d
$6 = 5+1$	$Spin(5,1) \simeq$ SL(2,H)	$\phantom{A}$ $\mathbb{H}$ the quaternions	little string
$10 = 9+1$	Spin(9,1) ${\simeq}$ “SL(2,O)”	$\phantom{A}$ $\mathbb{O}$ the octonions	heterotic/type II string

References

General

The definition is originally due to

• Arthur Cayley, On certain results relating to quaternions, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science Series 3 Volume 26, 1845 - Issue 171 (doi:10.1080/14786444508562684)

The formulation as the Dickson double construction is due to

• Leonard Dickson, On Quaternions and Their Generalization and the History of the Eight Square Theorem,

  Annals of Mathematics, Second Series, Vol. 20, No. 3 (Mar., 1919), pp. 155-171 (jstor:1967865)

Review:

• John Baez, The Octonions, Bull. Amer. Math. Soc. 39 (2002), 145-205. (web, pdf doi:10.1090/S0273-0979-01-00934-X)

Textbook accounts:

• Tonny Springer, Ferdinand Veldkamp, Octonions, Jordan Algebras, and Exceptional Groups, Springer Monographs in Mathematics, 2000 (doi:10.1007/978-3-662-12622-6)

• Tevian Dray, Corinne Manogue, The Geomety of Octonions, World Scientific 2015 (doi:10.1142/8456)

The concept of “special triples” or (“basic triples”) used above seems to go back to

• George Whitehead, appendix A in Homotopy Theory, MIT press 1971

Relation to the Leech lattice:

• Robert A. Wilson, Octonions and the Leech lattice, Journal of Algebra

  Volume 322, Issue 6, 15 September 2009, Pages 2186-2190, (pdf, slides)

Relation to 10d/11d spin geometry

Application of octonion-algebra to analysis of spin representations and spin geometry specifically in 11d (for general discussion in other dimensions see at supersymmetry and division algebras):

• John Huerta, Hisham Sati, Urs Schreiber, Real ADE-equivariant (co)homotopy and Super M-branes, Comm. Math. Phys. 371: 425. (2019) (arXiv:1805.05987)

• Hisham Sati, Urs Schreiber, Super-exceptional M5-brane model – Emergence of $SU(2)$-flavor sector, Journal of Geometry and Physics 170 (2021) 104349 [arXiv:2006.00012, doi:10.1016/j.geomphys.2021.104349]