nLab large cardinal

Idea

A large cardinal is a cardinal number that is larger than can be proven to exist in the ambient set theory, usually ZF or ZFC. Large cardinals arrange themselves naturally into a more or less linear order of size and consistency strength, and provide a convenient yardstick to measure the consistency strength of various other assertions that are unprovable from ZFC.

Set theorists often adopt the existence of certain large cardinals as axioms in the foundation of mathematics.

List of large cardinal conditions

• axiom of infinity– a large cardinal axiom relative to finitist theories, but not relative to ZF
• regular cardinal - a large cardinal in strongly predicative mathematics where function sets and power sets do not exist.
• beth fixed point? - a large cardinal in ETCS but small in ZF.
• axiom of replacement, an axiom schemata that states that certain families of sets or diagrams in the category of sets, which usually can be proven (for example, in Zermelo set theory or in a well-pointed topos) to be large or proper classes, are instead small. This implies that certain cardinals which previously were large are now small. Implies the existence of beth fixed points.
• inaccessible cardinal– the smallest sort of large cardinal in ZF, equivalent to the existence of a Grothendieck universe.
• Mahlo cardinal
• weakly compact cardinal?
• measurable cardinal– the boundary between “small” large cardinals and “large” large cardinals
• real-valued-measurable cardinal, a “solution” to the Banach–Ulam problem.
• strongly compact cardinal, whose existence controls properties images of accessible functors
• elementary embedding– a tool used in the study of large large cardinals
• supercompact cardinal
• extendible cardinal
• C(n)-extendible cardinal
• Vopěnka's principle– a large cardinal axiom with important implications for the behavior of locally presentable categories and accessible categories.

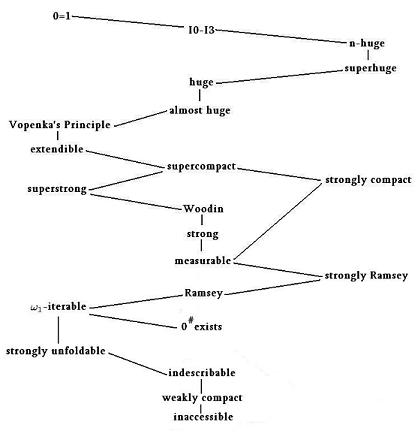
Here is a diagram showing the relation between these:

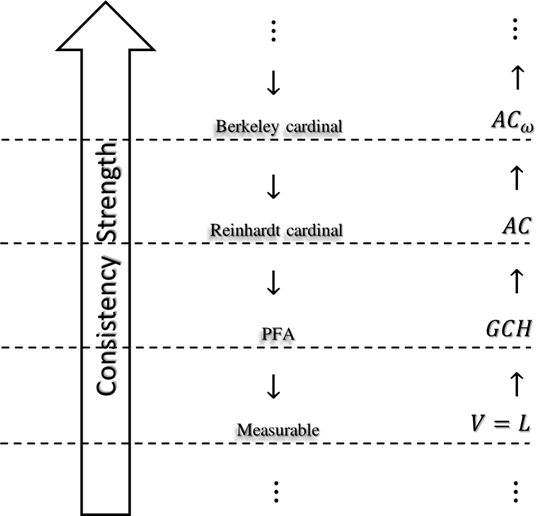
In the context of ZFC, certain axioms are inconsistent with large cardinal axioms:

References

• Wikipedia has a list of large cardinal properties.

A general axiomatic framework for large cardinal axioms is proposed in

• Arthur Apter, Carlos Diprisco, James Henle, William Swicker, Filter spaces: towards a unified theory of large cardinal and embedding axioms, Annals of Pure and Applied Logic Volume 41, Issue 2, 6 February 1989, Pages 93–106

• Arthur Apter, Carlos Diprisco, James Henle, William Swicker, Filter spaces. II. Limit ultraproducts and iterated embeddings, Acta Cient. Venezolana 40 (1989), no. 5-6, 311–318.