nLab
axiom of choice

Statement

In its modern category-theoretic form, the axiom of choice for a given category $C$ is the following statement:

• Every epimorphism in $C$ splits.

This means: for every epimorphism $f:A\to B$ there is a morphism $\sigma :B\to A$ (a section), such that

$$(B\stackrel{\sigma }{\to }A\stackrel{f}{\to }B)=(B\stackrel{{\mathrm{Id}}_B}{\to }B).$$(B \stackrel{\sigma}{\to} A \stackrel{f}{\to} B) = (B \stackrel{Id_B}{\to} B) \,.

Variations

• If $C$ is not balanced, such as a regular or coherent category which is not a pretopos, it may be more appropriate to replace in this statement “epimorphism” by regular epimorphism (or extremal epimorphism, effective epimorphism, etc.)

• More generally still, if $C$ is a site, then the axiom of choice for $C$ may be taken to say that any cover $U\to X$ admits a section. Obviously this refers only to singleton covers, but if $C$ is superextensive then any covering family $(p_i:U_i\to X{)}_i$ can be replaced by a singleton cover ${\coprod }_u{U}_i\to X$.

• When working in a category that has an internal logic, we may want to “internalize” the axiom of choice by asserting, not that every epimorphism has a section, but that the statement “every epimorphism has a section” is true in the internal logic. This is a weaker statement, but often it is the more relevant one.

Remarks

• If $C=$ Set then this reproduces the axiom of choice in its traditional form: an epimorphism $A\to B$ of sets can be regarded as a $B$-indexed family of sets. The existence of a section is equivalent to a choice of one element in each set of this family.

• Formulated in terms of sections, the axiom of choice may look less mysterious than in its original formulation. For instance, it is clear that it fails in contexts such as $C=$ Top and $C=$Diff, due to the existence of nontrivial topological and smooth fiber bundles.

• When the full axiom of choice fails, it may still be valid for some restricted class of objects $A$ and/or $B$. An object $B$ such that any epimorphism $A\to B$ splits is called projective; this means that one can make choices ‘indexed by’ $B$. Dually, an object $A$ such that one can make choices ‘with values in’ $A$ is called a choice object (this is not quite equivalent to every epimorphism $A\to B$ splitting).

• In the context of constructive mathematics, the full axiom of choice in $\mathrm{Set}$ implies the principle of excluded middle and so is rejected. However, weaker forms of choice, such as (in order of increasing strength) countable choice, dependent choice, and COSHEP, are often (if not usually) accepted by constructivists.

Equivalents

The following statements are all equivalent to the axiom of choice in $\mathrm{Set}$ (although sometimes the proof in one direction requires excluded middle). This is a very short list; much longer lists can be found elsewhere, such as at Wikipedia. Some of the statements on this list, though, may be of interest to nLabbers but are not commonly mentioned as equivalents of choice.

• The well-ordering theorem (that any set can be well-ordered),
• Zorn's lemma,
• That ($L=$ monomorphisms, $R=$ epimorphisms) is a weak factorization system on Set.
• That Set is equivalent to its own free exact completion.
• That there exists a group structure on every inhabited set (see this MO answer).

Variants

There are a number of weaker axioms which are implied by the full axiom of choice. Some of these are valid or accepted more generally than the full AC, and/or suffice for some of the usual applications of choice.

• Many applications of choice in logic, topology, and algebra require only the ultrafilter principle (UF), or equivalently the Boolean prime ideal theorem.

• From the perspective of constructive mathematics, the principle of excluded middle (EM) may be seen as a form of the axiom of choice; EM is equivalent to the statement that every Kuratowski-finite set is projective.

• The axioms of countable choice (CC) and dependent choice (DC) suffice for many of the usual applications of choice in the analysis of separable spaces. CC states that the set $\mathbb{N}$ of natural numbers is projective. DC strenghtens CC by allowing the set of possible choices for $n+1$ to depend on the choice made for $n$.

• The axiom COSHEP, also called the “presentation axiom,” says that any set admits a surjection from a projective one (whereas full AC says that all sets are projective). This implies CC and DC, and is moreover sufficient for the existence of projective resolutions and cofibrant replacements, as well as the usual theorems in algebra that (for example) Mod has enough projectives. For example, see the canonical model structure on Cat.

• The axiom of small violations of choice (SVC) asserts there is a set $S$ such that every set is a subquotient of $C\times S$ for some choice set $C$. Intuitively, this says that the failure of AC is parametrized by a single set. It can be regarded as a “dual” of COSHEP, since it deals with choice sets rather than projective ones, it implies the existence of (at least some) injective resolutions, and together with COSHEP and EM it implies full AC.

• The axiom of multiple choice is a different way of saying that choice is violated in only a small way, which is more “local” than SVC. It apparently follows from SVC, at least in ZF.

• The small cardinality selection axiom is another similar axiom. It asserts that there is a class function selecting for every set an isomorphic set (its “cardinality”) such that among each isomorphism class of sets, the collection of all “cardinalities” forms only a set.

• A still weaker axiom along the lines of “AC fails in only a small way,” which is implied by AMC, is WISC, i.e. that for any set $X$, the full subcategory of $\mathrm{Set}/X$ consisting of the surjections has a weakly initial set (under COSHEP it has a single weakly initial object, namely a projective cover of $X$). Two similar assertions are that the free exact completion ${\mathrm{Set}}_{\mathrm{ex}/\mathrm{lex}}$ of $\mathrm{Set}$ is a topos (i.e. that $\mathrm{Set}$ has a generic proof), and that ${\mathrm{Set}}_{\mathrm{ex}/\mathrm{lex}}$ is well-powered; both of these imply WISC.

The axiom of choice can also be strengthened in a few ways.

• While the ordinary axiom of choice says that any surjection of sets is split, the axiom of global choice says that this is also true for any surjection of proper classes. (Making this precise requires a bit of work.) It is equivalent to the existence of a well-ordering of the class of all sets.

• One can also postulate a choice operator, which gives a specified way to choose an element from any nonempty set. This implies global choice, and conversely a choice operator can be defined from any well-ordering of the class of all sets.

Finally, one can instead adopt the negation of the axiom of choice, or a strengthened version of this negation:

• The assumption that every subset of the real line has the Baire property (BP) is consistent with DC but not AC; the same holds for the assumption that every subset of the real line is measurable (LM) if at least one Grothendieck universe exists. These assumptions leads to a very nice setting for analysis called dream mathematics.

• The axiom of determinacy? is a natural statement in game theory that is consistent with dependent choice; in fact, it implies dependent choices in certain models, such as in the constructible (in the sense of Goedel) closure of the set of reals. However, determinacy contradicts full AC (for example, it implies LM and BP, as in the previous entry).

• Any of the varieties of constructive mathematics that contradict excluded middle necessarily contradict choice, but they are usually (if not always) consistent with DC (and even COSHEP).

In higher category theory

In 2-category theory one can consider the axiom of 2-choice.

Related concepts

• anafunctor;

• foundations.

References

• Eric Schechter's analysis book surveys several variants of AC and its negation with a view to applications of analysis, including this nice picture:

  

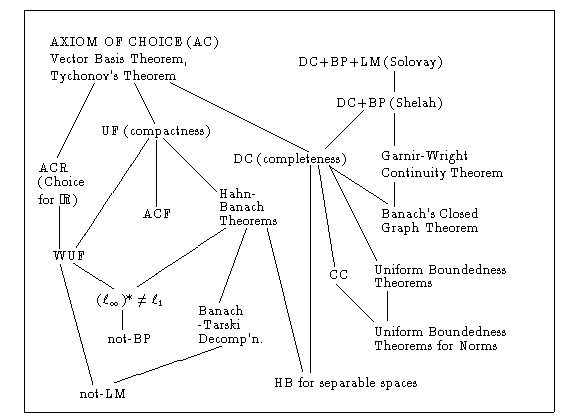
  (Here, UF, DC, CC, BP, and LM are as defined above.)

• Gonçalo Gutierres da Conceição, The Axiom of Countable Choice in Topology, pdf

  Despite the title, this covers more than countable choice, but the focus is on sequential aspects (metric spaces, first- and second-countable spaces, etc).

category: foundational axiom