nLab pillowcase orbifold

Definition

The pillowcase orbifold is the 2-dimensional flat (complex) orbifold which is the global quotient of the 2-torus by the reflection involution $z \mapsto -z$ on its canonical coordinates:

$$Pillow \;\coloneqq \; \mathbb{T}^2 \sslash_{refl} \mathbb{Z}_2 \;\coloneqq\; (\mathbb{R}^2/\mathbb{Z}^2) \sslash_{refl} \mathbb{Z}_2 \,.$$

(graphics from Dragomir 2011 Fig 2.6)

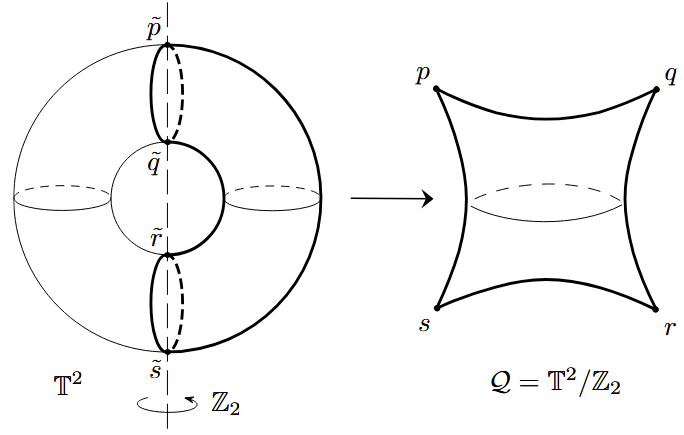
Properties

Coarse underlying space

The Weierstrass elliptic function $\wp$, regarded as a holomorphic function with values in the Riemann sphere $\mathbb{C}P^1$, exhibits the coarse underlying topological space of the pillowcase orbifold as the 2-sphere:

$$\wp \;\colon\; \mathbb{C}/\mathbb{Z}[i] \longrightarrow (\mathbb{C}/\mathbb{Z}[i])/_{refl} \mathbb{Z}_2 \overset{homeo}{\longrightarrow} \mathbb{C}P^1$$

(e.g Mukase 2004, end of §1.4, Eskin & Okounkov 2005, p. 1, Goujard & Moeller 2018, §2.3)

Related entries

• spindle orbifold

References

General

• Alex Eskin, Andrei Okounkov, Pillowcases and quasimodular forms, In: Ginzburg V. (ed.) Algebraic Geometry and Number Theory, Progress in Mathematics 253 Birkhäuser (2006) [arXiv:math/0505545, doi:10.1007/978-0-8176-4532-8_1]

• Elise Goujard, Martin Moeller, Pillowcase covers: Counting Feynman-like graphs associated with quadratic differentials [arXiv:1809.05016]

See also:

• George Dragomir: Closed Geodesics on compact developable orbifold, PhD thesis, McMaster University (2011) [pdf, pdf]

In string theory

On fluxed KK-compactification of D=6 supergravity on pillowcase orbifold fibers:

• Christoph Ludeling, 6D supergravity: Warped solution and gravity mediated supersymmetry breaking, PhD thesis, Hamburg (2006) [doi:10.3204/DESY-THESIS-2006-020]

• Gero von Gersdorff, Anomalies on Six Dimensional Orbifolds, JHEP 0703:083 (2007) [arXiv:hep-th/0612212]

• Markus Dierigl, Aspects of Six-Dimensional Flux Compactifications, PhD thesis, Hamburg (2017) [doi:10.3204/PUBDB-2017-09253]

and in the broader context of non-supersymmetric flat orbifolds of supergravity theories:

• Anamaria Font, Alexis Hernandez, Non-Supersymmetric Orbifolds, Nucl. Phys. B 634 (2002) 51-70 [arXiv:hep-th/0202057, doi:10.1016/S0550-3213(02)00336-X]