nLab universal Vassiliev invariant
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
A universal Vassiliev invariant is a Vassiliev knot invariant with coefficients in formal power series of Jacobi diagrams in Planck's constant whose leading term in on a given singular knot is its chord diagram.
By evaluating (framed) weight systems on the Jacobi diagram coefficients of a universal Vassiliev invariant it defines a function from framed weight systems on Jacobi diagrams, equivalently on round chord diagrams to actual (ground field-valued) Vassiliev knot invariants.
This construction in particular yields the proof that weight systems are the associated graded objects of Vassiliev invariants.
In principle there is a vector space of universal Vassiliev invariants, but all that appear in the literature tend to agree (BNGRT 97) and are identified (AF 96) with the un-traced Wilson loop observable of perturbative Chern-Simons theory:
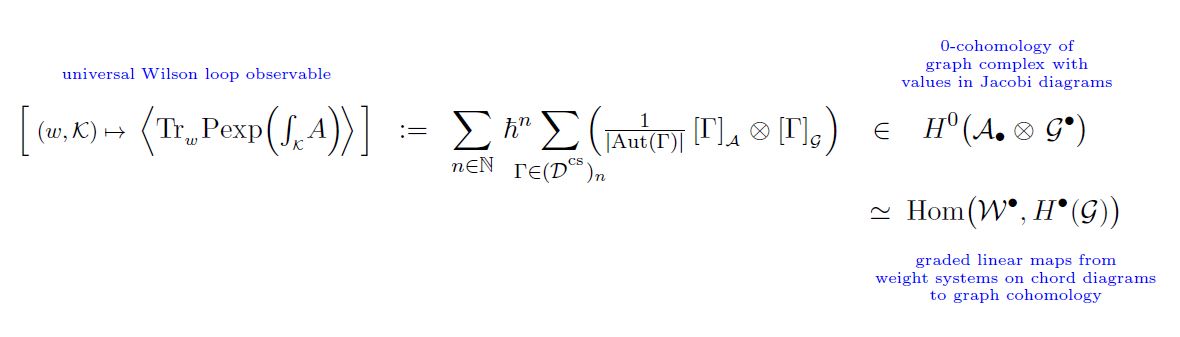

from Sati-Schreiber 19c
The main other known universal Vassiliev iunvariant is the Kontsevich integral (see Lescop 02 for the comparison).
Ingredients
Write
for the graded set of isomorphism classes of trivalent framed knot graphs – Feynman diagrams for Chern-Simons theory in the presence of Wilson loops, called “Wilson graphs” AF 96, Section 1, slightly differing from the un-framed knot graphs in CCRL 02.
By definition, a graph must have even number of vertices, and its degree is half that number (AF 96, (2.9))
For any write
for its automorphism group, a finite group whose order we denote by
Write
for the framed knot graph complex and
for the sub-vector space of its cohomology spanned by cocycles made of trivalent graphs.
Write
for the graded vector space of Jacobi diagrams modulo the STU-relations.
Also write
for the functions that send a graph to the defining basis vector that it represents in these vector spaces, respectively.
The space is the graded linear dual of the space of weight systems
Hence if we regard
as a cochain complex in non-positive degree with vanishing differential, then its tensor product of cochain complexes with the knot graph complex is the cochain complex whose closed elements are the graded linear maps from to the cochain cohomology of the knot graph complex:
Statement
Proposition
The element
(hence the sum over Feynman diagrams (1) of the tensor product of their images (5) in Jacobi diagrams modulo the STU-relations (4) and in the knot graph complex (3), respectively, weighted by the inverse order of their automorphism group (2) )
is closed
This is AF 96, Theorem 1.
Hence (7) defines a cochain cohomology-class
and hence, by (6), it defines a graded linear function
from weight systems on Jacobi diagrams (equivalently on round chord diagrams) to the cochain cohomology of the framed knot graph complex spanned by trivalent graphs.
According to CCRL 02, Prop. 7.6 this map is a bijection.
To see this, use 1) AF 96, Theorem 5, Condition U2 to find that the map is an injection, and 2) the fact that weight systems are associated graded of Vassiliev invariants.
Related concepts
References
General
Textbook account
- Christine Lescop, Invariants of links and 3-manifolds from graph configurations (arXiv:2001.09929)
Original articles:
-
Theorem 2.3 of: Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Le Tu Quoc Thang, Jun Murakami, The universal Vassiliev-Kontsevich invariant for framed oriented links, Compositio Math. 102 (1996), 42–64 (arXiv:hep-th/9401016)
-
Dror Bar-Natan, 4.4.2 of: On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)
-
Le Tu Quoc Thang, Jun Murakami, Representation of the category of tangles by Kontsevich’s iterated integral, Comm. Math. Phys., Volume 168, Number 3 (1995), 535-562. (euclid.cmp/1104272488)
-
Daniel Altschuler, Laurent Freidel, On Universal Vassiliev Invariants, Commun. Math. Phys. 170 (1995) 41-62 [arXivhep-th/9403053, doi:10.1007/BF02099438]
-
Daniel Altschuler, Laurent Freidel, Theorem 5 of: Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187* (1997) 261-287 [arXiv:q-alg/9603010, doi:10.1007/s002200050136]
-
Le Tu Quoc Thang, Jun Murakami, Tomotada Ohtsuki, On a universal perturbative invariant of 3-manifolds, Topology 37 3 (1998) 539-574 [doi:10.1016/S0040-9383(97)00035-9]
Review:
-
Dror Bar-Natan, Alexander Stoimenow, The Fundamental Theorem of Vassiliev Invariants (arXiv:q-alg/9702009)
-
Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Section 8.8 of: Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)
-
David Jackson, Iain Moffat, Section 18 of: An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)
Comparison
Comparison between the two main universal Vassiliev invariants: the Kontsevich integral and the Wilson loop observable of perturbatively quantized Chern-Simons theory:
- Christine Lescop, On configuration space integrals for links, Geom. Topol. Monogr. 4 (2002) 183-199 (arXiv:math/0211062)
Special values
Computation of the perturbative Chern-Simons Wilson loop observable (universal Vassiliev invariant) of the unknot (“Wheels theorem”):
- Dror Bar-Natan, Le Tu Quoc Thang, Dylan Thurston, Two applications of elementary knot theory to Lie algebras and Vassiliev invariants, Geom. Topol. Volume 7, Number 1 (2003), 1-31 (euclid.gt/1513883092)
following
- Dror Bar-Natan, Stavros Garoufalidis, Lev Rozansky, Dylan Thurston, Wheels, wheeling, and the Kontsevich integral of the unknot (q-alg/9703025)
Last revised on July 17, 2024 at 16:27:18. See the history of this page for a list of all contributions to it.