nLab weight systems are cohomology of knot graph complex
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
The cochain cohomology of the framed knot graph complex (sometimes called the “Wilson graph complex”) spanned by trivalent graphs coincides with the space of framed weight systems on Jacobi diagrams, equivalently on round chord diagrams:
This statement is made explicit as CCRL 02, Prop. 7.6, where it is noticed that this is implicit in statement and proof of AF 96, Theorem 1 (where in turn the argument is attributed to Kohno 94!)
Moreover:
If is a weight system and is a Jacobi diagram such that , then its image under the above isomorphism contains a non-vanishing multiple of as a summand.
This is made explicit as CCRL 02, Remark 7.7 and again this is implicit in the statement of AF 96, Theorem 1.
What AF 96 explicitly construct is a universal Vassiliev invariant, which they identify with the un-traced Wilson loop observable
of perturbative Chern-Simons theory.
Ingredients
Write
for the graded set of isomorphism classes of trivalent framed knot graphs – Feynman diagrams for Chern-Simons theory in the presence of Wilson loops, called “Wilson graphs” AF 96, Section 1, slightly differing from the un-framed knot graphs in CCRL 02.
By definition, a graph must have even number of vertices, and its degree is half that number (AF 96, (2.9))
For any write
for its automorphism group, a finite group whose order we denote by
Write
for the framed knot graph complex and
for the sub-vector space of its cohomology spanned by cocycles made of trivalent graphs.
Write
for the graded vector space of Jacobi diagrams modulo the STU-relations.
Also write
for the functions that send a graph to the defining basis vector that it represents in these vector spaces, respectively.
The space is the graded linear dual of the space of weight systems
Hence if we regard
as a cochain complex in non-positive degree with vanishing differential, then its tensor product of cochain complexes with the knot graph complex is the cochain complex whose closed elements are the graded linear maps from to the cochain cohomology of the knot graph complex:
Statement
Proposition
The element
(hence the sum over Feynman diagrams (1) of the tensor product of their images (5) in Jacobi diagrams modulo the STU-relations (4) and in the knot graph complex (3), respectively, weighted by the inverse order of their automorphism group (2) )
is closed
This is AF 96, Theorem 1.
Hence (7) defines a cochain cohomology-class
and hence, by (6), it defines a graded linear function
from weight systems on Jacobi diagrams (equivalently on round chord diagrams) to the cochain cohomology of the framed knot graph complex spanned by trivalent graphs.
According to CCRL 02, Prop. 7.6 this map is a bijection.
To see this, use 1) AF 96, Theorem 5, Condition U2 to find that the map is an injection, and 2) the fact that weight systems are associated graded of Vassiliev invariants.
In summary we have the following situation:
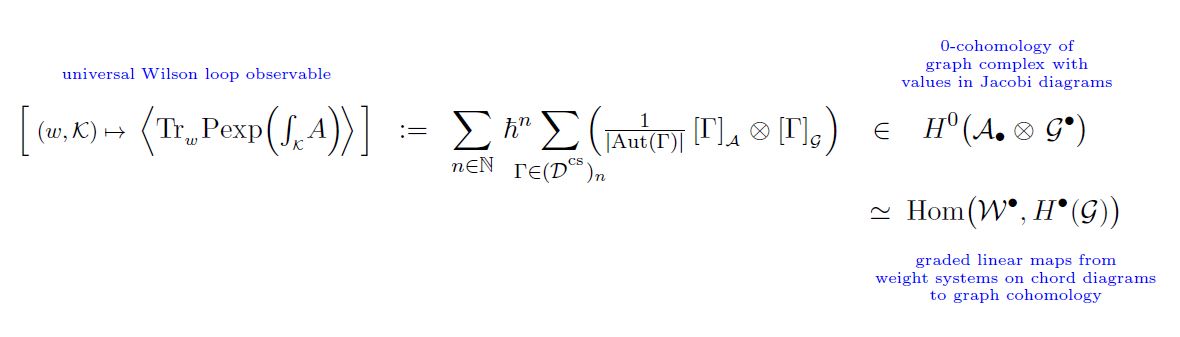

graphics from Sati-Schreiber 19c
Related theorems
Facts about chord diagrams and their weight systems:
References
-
Toshitake Kohno, Vassiliev invariants and de Rham complex on the space of knots,
In: Yoshiaki Maeda, Hideki Omori, Alan Weinstein (eds.), Symplectic Geometry and Quantization, Contemporary Mathematics 179 (1994): 123-123 (doi:10.1090/conm/179)
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arXiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
Computation of the perturbative Wilson loop observable (universal Vassiliev invariant) of the unknot (“Wheels theorem”):
- Dror Bar-Natan, Thang T Q Le, Dylan Thurston, Two applications of elementary knot theory to Lie algebras and Vassiliev invariants, Geom. Topol. Volume 7, Number 1 (2003), 1-31 (euclid.gt/1513883092)
following
- Dror Bar-Natan, Stavros Garoufalidis, Lev Rozansky, Dylan Thurston, Wheels, wheeling, and the Kontsevich integral of the unknot (q-alg/9703025)
Last revised on April 25, 2021 at 07:19:05. See the history of this page for a list of all contributions to it.