Schreiber Categories and Toposes
This page is to record the lecture series:
-
Categories and Toposes – Differential cohesive higher Toposes
lecture series at
Modern Mathematics Methods in Physics:
Diffeology, Categories and Toposes and Non-commutative Geometry Summer SchoolNesin Mathematics Village — Şirince, Izmir, Turkey
(June 18-29, 2018)
from basics of category theory and topos theory, to higher supergeometry organized via differential cohesion, with indication of applications to perturbative quantum field theory and fundamental super p-branes.

Introduction
The geometry of fundamental physics is higher differential supergeometry.
| physics | mathematics |
|---|---|
| gauge principle | higher geometry (geometric homotopy theory) |
| Pauli exclusion principle | supergeometry |
Here:
-
Supergeometry is geometry whose spaces may have algebras of functions that are -graded-commutative algebras. This is the mathematical reflection of the Pauli exclusion principle, which says that a fermionic wave function on a phase space of a physical system with fermions has to have vanishing square. By linearity this implies that
and hence that fermionic wave functions anti-commute, and hence are the odd-graded elements in a commutative superalgebra (a slightly noncommutative algebra!)
Ever since the existence of fermionic particles was experimentally established, around the time of the Stern-Gerlach experiment in the 1920s, it is thus an experimental fact that fundamental physics is described by supergeometry. (This is not necessarily super-symmetric, though of course there is a close relation.)
-
Higher structures is short for higher homotopy theoretic structures and reflects the gauge principle of physics: This says that, generally, it does not make invariant sense to ask if any two things , (e.g. field histories) are equal, instead one must ask for a gauge transformation between them, mathematically a homotopy:
This principle applies also to gauge transformations themselves, and thus leads to gauge-of-gauge transformations
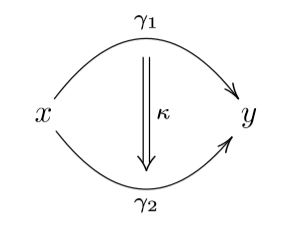
and so on to ever higher gauge transformations:
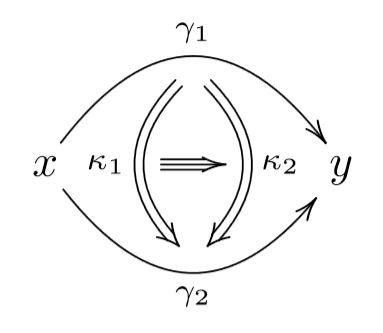
mathematically reflected by higher homotopies in higher homotopy types.
Ever since the existence of gauge fields was understood in the 1920s, it is thus an experimental fact that fundamental physics is described by higher geometry.
A striking consequence is that, both in higher geometry as well as in supergeometry and therefore in the geometry of fundamental physics, spaces generally are not sets of points, as in the traditional definition of topological spaces or differentiable manifolds.
What, then, is the geometry of fundamental physics?
The right framework to answer questions like this has been urged by Alexander Grothendieck already in Grothendieck 73 (see Lawvere 03) and has been much expanded on by William Lawvere (e.g. Lawvere 97, Lawvere 91) and has an evident lift to higher geometry (Lurie 09, S. 13), but has remained somewhat of a “public secret”:
The answer is known, alternatively, as (higher) functorial geometry (Grothendieck) or synthetic differential geometry in gros toposes (Lawvere), or variants thereof.
In this lecture series we try to give a quick but self-contained introduction to higher differential supergeometry this way, following Schreiber 13. We begin at the beginning, with introducing relevant basics of category theory and topos theory and will provide brief indication of real-world applications to perturbative quantum field theory and fundamental super p-branes.
The outline of the lecture follows these four chapters of the larger set of lectures geometry of physics:
and will variously point for further reading on applications to these chapters:
The higher differential geometry which we lay out subsumes various special cases that are discussed separately in the literature. Notably the diffeological spaces discussed by Patrick Iglesias-Zemmour in a parallel lecture (pdf) find home and company here: We explain how these are equivalently the concrete objects among the the bosonic smooth h-sets:
and we discuss how, even if one is initially interested only in ordinary smooth manifolds or only in diffeological spaces, it is useful to work with more general super differential homotopy types.

graphics taken from Higher Prequantum Geometry
Last revised on May 1, 2025 at 10:24:55. See the history of this page for a list of all contributions to it.