nLab geometry of physics -- supergeometry
this entry is one section of “geometry of physics – supergeometry and superphysics”
which is one chapter of “geometry of physics”
previous sections: superalgebra, categories and toposes, smooth sets
following sections: geometry of physics – supersymmetry, geometry of physics – smooth homotopy types
Supergeometry is the generalization of differential geometry (or algebraic geometry) to the situation where algebras of functions are generalized from commutative algebras to supercommutative superalgebras.
In geometry of physics – superalgebra we discussed why it is mathematically compelling to pass to supercommutative superalgebra and how this implies a dual concept of superspace in terms of affine superschemes. Here we discuss how to build a fully-fledged theory of geometry on these affine superspaces – supergeometry – in parallel to the discussion of ordinary differential geometry in geometry of physics – smooth sets.
Apart from the abstract mathematical motivation for supergeometry, it is also an experimental fact that the observable universe is fundamentally described by supergeometry. Namely the Pauli exclusion principle, in its refined form of the spin-statistics theorem, implies that the phase space of a field theory (already of a classical field theory) with fermion fields (such as that of electrons and quarks) is a superspace whose even-graded coordinates are the configurations of the boson fields, while the odd-graded coordinates correspond to the configurations of the fermion fields. It is impossible to have an action functional for fermion fields as a function on a non-super (infinite-dimensional)-manifold.
This is an old insight: The experimental detection of the special properties of fermions that show their super-geometric nature goes back all the way to the Stern-Gerlach experiment in 1922, which revealed that electrons are spinors. The Pauli exclusion principle (Pauli 1925) – deduced from the nature of energy levels of electrons in atoms – says that no two such spinors may occupy the exact same quantum state. Technically this says that the spinor field variable has to satisfy
A little later it was realized that the axioms of local field theory imply that all spinor fields need to be fermions in that for any two classical spinor field variables , the Grassmann sign rule holds (Grassmann 1844):
(which of course immediately implies the Pauli exclusion principle). This is the celebrated spin-statistics theorem, whose formulation goes back to Fierz in 1939 and Pauli in 1940. And that sign rule is of course precisely the sign rule in a supercommutative superalgebra, for the fermion field observables being odd-graded functions on a supergeometric phase space.
Notice that this phenomenon is not a negligible subtlety: the Pauli exclusion principle is what implies stability of matter by forcing electrons in an atom to fill up “orbitals” consecutively as opposed to all falling into the ground state, as a bosonic condensate would do. There would be no solid state physics without supergeometry of phase spaces, no solid matter. (In addition, the Pauli degeneracy pressure controls more exotic phenomena, for instance the stability of neutron stars against their gravitational collapse.)
As a slogan:
The geometry of phase spaces for fermions,
hence for matter fields admitting solid states,
is supergeometry.
Nevertheless, few textbooks make the supergeometric aspect in the physics of fermions explicit. Some discuss it only after quantization (and some will even claim that fermion fields do not exist classically); some only discuss it in the context of spacetime supersymmetry. But notice that supergeometry is a subject in itself even without presence or mentioning of spacetime supersymmetry (which is super Poincaré group symmetry), just as differential geometry is a subject in itself even without the presence or mentioning of Poincaré group symmetry. Hence this we discuss independently in geometry of physics – supersymmetry.
Texts which do make the super-geometric nature of fermion fields explicit include
This we discuss elsewhere.
Context
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Supergeometry
In the section geometry of physics – superalgebra we had discussed the category of affine super schemes (in this definition)
Here we use these as local model spaces to develop geometry locally modeled on affine superschemes. Since we are interested in physics, and since spacetimes and phase spaces in physics are objects in differential geometry, not in algebraic geometry (even if sometimes they may come from there), we consider the full subcategory of super Cartesian spaces (this example)
whose algebras of functions by definition are tensor products (over the real numbers ) of -algebras of smooth functions with Grassmann algebras
These serve as our “abstract super-coordinate systems” that define supergeometry in direct analogy to how ordinary Cartesian spaces serve as the abstract coordinate systems that define differential geometry as found at geometry of physics – coordinate systems and_geometry of physics – smooth sets.
Then a general superspace is modeled as a sheaf on the category of super Cartesian spaces, possibly satisfying some suitable properties. see remark below for explanation of this perspective.
This means that we follow the perspective of “functorial geometry” due to Grothendieck 65, where a scheme is regarded as a sheaf over the category of affine schemes (its “functor of points”) satisfying the condition that it is covered by (representables of) affines via formally étale morphism. We explain all this below.
Beware that – despite the urging in Grothendieck 73 that the definition of schemes as locally ringed spaces should be abandoned in favour of the perspective of functorial geometry – most textbooks on supergeometry do stick with the point of view of locally ringed spaces. (One might argue that in smooth supergeometry this is a particularly heavy violation of Grothendieck’s urging, since, in contrast to algebraic schemes, every supermanifold is already affine.)
An exception is the approach propagated in Schwarz 84, Molotkov 84, Konechny-Schwarz 97 of which a clean account is given in Sachse 08. These authors consider (pre-)sheaves on the category of superpoints. This gives the “super” in “super-geometry” a functorial interpretation, but the (smooth) “geometry” still needs to be added in by hand. Hence this approach satisfies Grothendieck’s urging half-way.
The full application of the perspective of functorial geometry to supergeometry is known as synthetic differential supergeometry, where one considers sheaves over the full category of formal super Cartesian spaces (Yetter 88, section 3). This is essentially the perspective which we adopt here. We do however not refer to the (super-)Kock-Lawvere axioms for synthetic differential geometry but instead use the axiomatics of “differential cohesion” (Schreiber 13). This we explain below.
Super Cartesian spaces
For reference, recall:
Definition
For , the real Grassmann algebra
is the -algebra freely generated from generators (now regarded as being in odd degree), subject to the relations
for all . In particular
for all (since has characteristic zero and in particular ).
For , the super-Cartesian space is the formal dual of the supercommutative superalgebra written or whose underlying -graded vector space is
with the product given by the relations
where is the ordinary pointwise product of smooth functions:
Write
for the full subcategory of the opposite category of commutative superalgebras on those of this form. We write for the formal dual of .
Moreover, we write
for the full subcategory on ordinary Cartesian spaces with smooth functions between them. These are the “abstract coordinate charts” from the discussion at geometry of physics – smooth sets, and so we are evidently entitled to think of the objects in as abstract super coordinate systems and to develop a geometry induced from these.
Recall the three magic algebraic properties of smooth functions that make the above algebraic description of differential geometry work:
Proposition
(first two magic properties of algebras of smooth functions)
-
(embedding of smooth manifolds into formal duals of R-algebras)
The functor that assigns algebras of smooth functions to smooth manifolds
is fully faithful (this Def.).
-
The functor that assigns smooth sections of smooth vector bundles of finite rank
is fully faithful (its essential image being the finitely generated projective modules over the -algebra of smooth functions).
Moreover, the modules over the -algebra of smooth functions on which arise this way as sections of smooth vector bundles over a Cartesian space are precisely the finitely generated free modules over .
There is a third such magic algebraic property of smooth functions, which plays a role now:
Proposition
(derivations of smooth functions are vector fields)
Let be a smooth manifold. Write
for the function that sends a smooth vector field to the derivation of the algebra of smooth functions on given by forming derivatives: . This is a derivation by the chain rule.
Then this function is a bijection, hence every derivation of comes from differentiation along some smooth vector field, which is uniquely defined thereby.
Proof
By the existence of partitions of unity we may restrict to the situation where is a Cartesian space. By the Hadamard lemma every smooth function may be written as
for smooth functions with . Since any derivation by definition satisfies the Leibniz rule, it follows that
Similarly, by translation, at all other points. Therefore is already fixed by its action of the coordinate functions . Let be the vector field
then it follows that is the derivation coming from under .
Recall further from geometry of physics – superalgebra that the category of supercommutative superalgebras is related to that of ordinary commutative algebras over by an adjoint cylinder (this prop.):
Proposition
(adjoint modality of even fermionic and bosonic in superalgebras)
The canonical inclusion of commutative algebras into supercommutative superalgebras is part of an fully faithful adjoint triple (this Def.) of the form
(Here and in the following we display pairs of adjoint functors (this Def.) such that the left adjoint is on top and the right adjoint is on the bottom.)
The formal dual (this Def.) of this statement is that affine superschemes are related to ordinary affine schemes over by an adjoint modality of this form
Beware that
-
is the formal dual of ,
-
is the formal dual of .
That they change position in the diagrams is because we always draw left adjoints on top of right adjoints and the handedness of adjoints changes as we pass to opposite categories.
Example
The algebra of functions on is
where in the last line we renamed to .
This algebra is known as the algebra of dual numbers over . It is to be thought of as the algebra of functions on a bosonic but infinitesimally thickened point, an infinitesimal neighbourhood of a point inside the real line which is “so very small” that the canonical coordinate function on it takes values “so tiny” that its square, which is bound to be even tinier, is actually indistinguishable from zero.
We will write
for the space formally dual to this algebra of dual numbers and think of it as the 1-dimensional first order infinitesimal disk.
In generalization of this we make the following definitions:
Definition
Write
for the full subcategory (this Example) of the opposite category (this Example) of commutative algebras over on formal duals of commutative algebras over the real numbers of the form
with a nilpotent ideal of finite-dimension over (the direct sum on the right is that of underlying vector spaces, not of algebras).
We call this the category of infinitesimally thickened points.
Alternative terminology:
-
In synthetic differential geometry these algebras are called Weil algebras,
-
in algebraic geometry they are known as local real Artin algebras.
Write moreover
for the full subcategory on formal duals of those algebras which are tensor products of commutative -algebras of the form
of algebras of smooth functions with algebras corresponding to infinitesimally thickened points as above.
Remark
(formal schemes and synthetic differential geometry)
This kind of construction in Def. is traditionally more familiar from the theory of formal schemes, but the same kind of general abstract theory goes through in the context of differential geometry, a point of view known as synthetic differential geometry (Lawvere 97), preconfigured already in the prespective of functorial geometry of Grothendieck 65.
The crucial property of infinitesimally thickened points (def. ) is that they co-represent tangent vectors and jets:
Example
(morphisms out of infinitesimally thickened point are tangent vectors)
Write for the formal dual of the algebra of dual numbers (example ). Then morphisms in (def. ) of the form
which are the identity after restriction along , are in natural bijection with smooth vector fields on .
Moreover, morphisms of the form
are equivalently single tangent vectors, hence for every there is a natural bijection
between the hom-set from the formal dual of the ring of dual numbers and the set of tangent vectors.
Proof
By definition, morphisms
which are the identity after restriction along , are equivalently algebra homomorphisms of the form
which are the identity modulo . Such a morphism has to take any function to
for some smooth function . The condition that this assignment makes an algebra homomorphism is equivalent to the statement that for all
Multiplying this out and using that this in turn is equivalent to
This means equivalently that is a derivation. But derivations of smooth functions are vector fields (prop. ).
We now explore further the relations between Cartesian spaces, formal Cartesian spaces, and super formal Cartesian spaces.
Proposition
(co-reflection of Cartesian spaces inside formal Cartesian spaces)
The canonical inclusion of the category of ordinary Cartesian spaces into that of formal Cartesian spaces has a left adjoint (this Def.) (“reduction”)
given by
Hence exhibits as a coreflective subcategory (this Def.) of
We say that is the reduced scheme of .
Proof
We check the natural isomorphism on hom-sets that characterizes a pair of adjoint functors (here):
By definition, a morphism of the form
is equivalently a homomorphism of commutative algebras of the form
where all elements are nilpotent, in that there exists such that . Every algebra homomorphism needs to preserve this equation, and hence needs to send nilpotent elements to nilpotent elements. But the only nilpotent element in the ordinary function algebra is the zero-function, and so it follows that the above homomorphism has to vanish on all of , hence has to factor (necessarily uniquely) through a homomorphism of the form
This is dually a morphism of the form
in . This establishes a natural bijection .
The above discussion following prop. means that in passing to commutative superalgebras there are two stages of generalizations of plain differential geometry involved:
-
Cartesian spaces are generalized to formal Cartesian spaces;
-
formalCartesian spaces are further generalized to super formal Cartesian spaces.
In order to make this explicit, it is convenient to introduce the following slight generalization of super Cartesian spaces (def. ), which are simply Cartesian products of ordinary Cartesian spaces with an infinitesimally thickened point that may have both even and odd graded elements in its algebra of functions.
Definition
(super formal Cartesian spaces)
Write
for the full subcategory (this Example) of that of the opposite category of supercommutative superalgebras on those which are tensor products of commutative algebras of
-
the algebra of smooth functions on a Cartesian space,
-
a Grassmann algebra (Def. ),
-
a Weil algebra (Def. )
One place in the literature where such super formal Cartesian spaces are made explicit is in Konechny-Schwarz 97.
Just as formal Cartesian spaces may be thought of as local model spaces for synthetic differential geometry, super formal Cartesian spaces may be thought of as a model for synthetic differential supergeometry. This we come to below.
For completeness it is useful to compare the coreflection of prop. to the following simple reflection.
Write
for the category with a single object and a single morphism (the identity) on that object. We will think of this as the category containing just the point space, which we want to think of as the local model space for discrete geometry.
Proposition
There is a pair of adjoint functors
into the category of Cartesian spaces, where the bottom functor sends the unique object to the point , and where its left adjoint on top is, necessarily, the unique functor constant on the unique object on the left.
Proof
The natural isomorphism between hom sets characterizing this pair of adjoint functors simply expresses the fact that is the terminal object in , hence that for any Cartesian space, then there is a unique smooth function of the form .
In conclusion, the various extra structures on local model spaces (abstract coordinate systems) which we considered are organized in the following diagram:
Proposition
(progression of (co-)reflective site-inclusions)
The coreflective subcategory inclusion of Cartesian spaces into formal Cartesian spaces from prop. and the coreflective as well as reflective subcategory inclusion of affine schemes into affine superschemes from prop. and the terminal inclusion of prop. combine to give the following system of adjoint functors on our local model spaces
Super smooth sets
Above we discussed (formal) super Cartesian spaces. What we are after is geometry of generalized space which is “locally modeled” on these, in the sense explained in the chapter on categories and toposes . In order to do so we
-
consider generalized superspaces whose collection forms a “good category” (the sheaf topos over super Cartesian space) in that lots of universal constructions on general superspaces (limits, colimits) still yield general superspaces;
-
use special properties of this nice category (differential cohesion) in order to characterize and construct the good, tame superspaces, such as actual supermanifolds.
The construction proceeds in direct anology to the non-super version discussed in the chapters on smooth sets and on manifolds and orbifolds. For reference we first briefly recall this bosonic situation.
The following simple definitions and are key to the whole theory. They embody the perspective of functorial geometry (Grothendieck 65). See remark below for exegesis and illustration.
Definition
(CartSp)
Write CartSp for the category of Cartesian space for with smooth functions between them. Say that a collection of morphisms in is covering if this is a good open cover in that every finite non-empty intersection of the charts is diffeomorphic to a Cartesian space. This defines a coverage on CartSp and hence makes it a site.
Definition
We say a smooth set (this Def.ets#CategoryOfSmoothSets)) is, equivalently, a sheaf on CartSp (Def. ), according to this Prop.ets#SmoothSetsAreSheavesOnCartSp). We write
for the sheaf topos (this Def.) of smooth set.
Remark
The useful way to think of def. in the present context is as defining a kind of generalized smooth space which is defined by which smooth functions from Cartesian spaces it receives (see also at motivation for sheaves, cohomology and higher stacks for more exposition of this point).
Namely a smooth set in the sense of def. is first of all a rule
which assigns a set to each Cartesian space. We are to think of this set as the set of smooth functions {“”}, only that there is no pre-defined concept of smoothness of functions into , instead it is defined by that very rule. Moreover, for every smooth function between Cartesian spaces, there is to be a corresponding function between these sets, going in the opposite direction
which we are to think of as being the precomposition operation
This is required to satisfy the evident conditions that composition and identity is respected, in that and . Together these conditions say that is a presheaf on the category of test spaces – the “functor of points” (Grothendieck 65).
In addition, the requirement that be a sheaf on the site of Cartesian spaces from def. means that the assignment knows that one coordinate system may be covered by other coordinate systems. Namely let be an open cover by open balls (each of which may be identified with itself, by a diffeomorphism) then the condition is that the function
is a bijection from to the subset of the Cartesian product of those tuples of functions which coincide on all intersections: (“matching families”).
For example every Cartesian space defines a smooth set by the rule
which says that the set of would-be smooth functions into is the actual set of smooth functions into . One also says that represents a sheaf on ,
This defines a full subcategory inclusion of Cartesian spaces into smooth sets
called the Yoneda embedding.
The same construction works for any smooth manifold: it is regarded as a smooth set defined by the rule
which assigns actual sets of smooth functions.
Notice that since Cartesian spaces (and smooth manifolds) themselves are understood as special cases of smooth sets, there now appears an actual concept of smooth functions of the form , for every smooth set , without quotation marks: namely this is a morphism in the category of smooth sets.
Now there might be a worry: given any smooth set and any Cartesian space , we seem to have two different concepts of what the set of smooth functions from to is: the set of “smooth functions by fiat” (maps with quotation marks) and the actual hom-set (maps without quotation mark).
That these two sets are in fact in natural bijection, hence that the interpretation of a sheaf as a generalized smooth space is consistent, is the statement of the Yoneda lemma:
Hence the Yoneda lemma says that we may remove the quotation marks:
Remark
The strategy is now to work in the nice category of generalized smooth spaces (a topos), and find in there full subcategories of more specific types of smooth spaces having extra properties which one may need in given applications. There is a long list of such subcategories of relevance, some of these we briefly discuss now:
Cartesian spaces smooth manifolds Hilbert manifolds Banach manifolds Fréchet manifolds diffeological spaces smooth sets formal smooth sets super formal smooth sets
and similarly for their supergeometric version (which we turn to below, def. )
Cartesian spaces super Cartesian spaces supermanifolds super smooth sets .
By the strategy of remark we now pass to generalized spaces which are locally modeled not just on plain Cartesian spaces, but also on formal Cartesian spaces and super formal Cartesian spaces
Definition
Define a coverage on the categories (def. ) and on (def. ) by declaring the covering families of any object (hence for with any infinitesimally thickened superpoint) to be those of the form
for
a good open cover as in def. .
In analogy with def. we say that
- a sheaf on is a formal smooth set or formal smooth 0-type and we write
for the sheaf topos of all of these;
- a sheaf on is a super formal smooth set or super formal smooth 0-type and we write
for the sheaf topos of all of these;
The category of formal smooth sets from def. is often known as the Cahiers topos. It was introduced in (Dubuc 79) as a well-adapted model for the Kock-Lawvere axioms for synthetic differential geometry. The category of super formal smooth sets from def. was considered in Yetter 88, called the super Dubuc topos there.
We have now defined four sites and considered the corresponding categories of sheaves (noticing that Set)
Moreover, by prop. these four sites form a filtration of the site by consecutively smaller subsites, where each inclusion is either reflective or coreflective or both. The following states that this filtration of sites extends to their categories of sheaves.
Proposition
(progression of (co-)reflective subcategories of SuperFormalSmoothSet)
The sheaf topos SuperFormalSmoothSet (Def. ) is a solid topos over FormalSmoothSet, in that:
There exists an essentially unique system of functors between the categories of sets, smooth sets (def. ), formal smooth sets and super formal smooth sets (def. ) as shown in the second and third row of the following diagram, such that
-
every pair of consecutive functors is an adjoint pair (this Def.), with the functor above being left adjoint and the functor below being right adjoint
-
on representables the top two functors on the left, the top two functors in the middle, and the top three functors on the right coincide with the corresponding functors between sites shown in the first row (from prop. ):
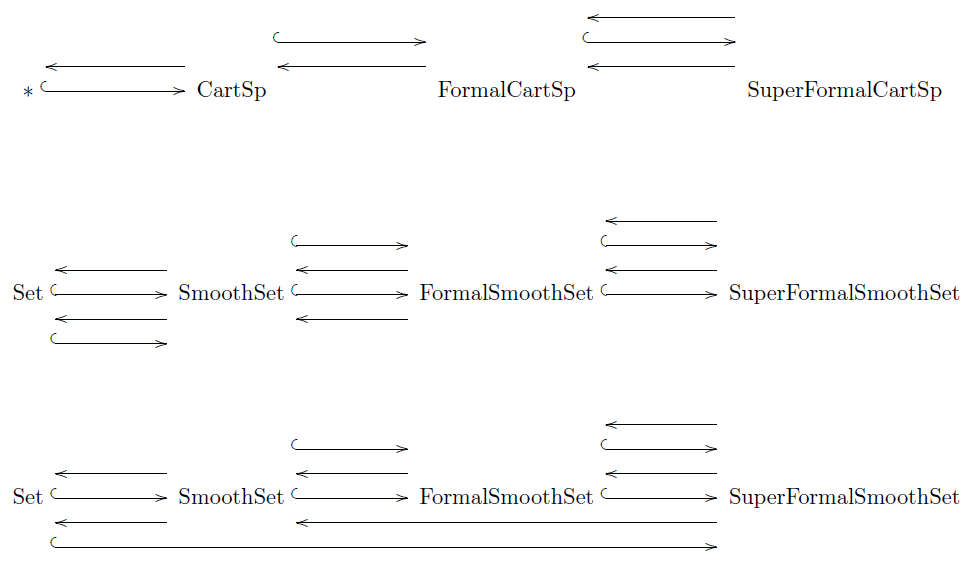
In such a situation we also say that in the third row
-
the bottom four functors exhibit SuperFormalSmoothSet as a cohesive topos (this Def.)
-
the middle four functors exhibit SuperFormalSmoothSet as differentially cohesive topos (elastic topos) relative to SmoothSet (this Def.);
-
the top four functors exhibit as solid topos relative to FormalSmoothSet (this Def.)
Proof
The system of functors between sites in Prop.
induces the claimed adjoint quadruples between presheaf toposes in the second row, by Kan extension (this Example in the chapter on categories and toposes).
That the adjoint quadruple on the left (co-)restricts to sheaves, exhibiting SmoothSet as a cohesive topos, is this Prop. in the chapter on smooth sets.
For the other two adjoint quadruples the (co-)restricts to sheaves is trivial, since this concerns only the coverages along the infinitsimal directions in FormalCartSp and SuperFormalCartSp, which are trivial (this Example), by definition.
This establishes the system of adjoint quadruples between sheaf toposes in the second row.
The diagram in the third row states that two extra adjoints to composites of the functors appear. Here
-
the right adjoint functor
exists as part of the adjoint quadruple which is induced (this Example) from the composite coreflective inclusion
and using that composites of adjoints are adjoint, and that adjoints are unique, when they exist (this prop.)
-
Notice that also SuperFormalCartSp is a cohesive site: since the coverage along the infinitesimal directions is trivial, while that along the finite directions is the same as that on CartSp, this follows with the same proof as for CartSp (this Prop.).
Moreover, the composite
from the second row above equals the functor
which is part of the adjoint quadruple of the cohesion of (via that Prop.)): This is because all these inclusion functors are right adjoints, and hence preserve the terminal object (this Prop.), but also left adjoints, and hence preserved limit coproducts (this Prop.). This implies the claim because every set is a coproduct of the singleton, which is the terminal object in Set.
This implies, again by uniqueness of adjoints (this Prop.) that the composite functor from the previous item is in fact the functor from the cohesive topos-structure on SuperFormalSmoothSet and hence, finally, that there is the bottom right adjoint
as claimed.
Finally, that every second functor is a full subcategory inclusion (a fully faithful functor) as shown follows because
-
left Kan extension along fully faithful functors is itself fully faithful (this prop.);
-
in an adjoint triple the leftmost adjoint is fully faithful precisely if the rightmost adjoint is (this prop.).
Proposition says that the basic operations on local model spaces, such as
-
forming the underlying bosonic space,
-
forming the underlying formal bosonic space of bi-fermions,
-
forming the underlying reduced space
extend from local model spaces to the generalized spaces modeled on them, while retaining their relation to each other and to the respective inclusions, and such that yet further operations accompanying them are induced.
To record what all these operations are, it is useful to compose the functors above in pairs, with one functor projecting down to the left, and the next one including back with either a left or right adjoint of the projection.
For example given a generalized superspace, then applying the top-most functor in prop. to it yields its underlying bi-fermionic formal smooth space, regarded as an object in FormalSmoothSet. But if we work in supergeometry, then we want this result to be understood as a superspace again, one that just so happens to have no odd directions, so we re-include it by the inclusion right adjoint to the top projection. This composite operation of projection and re-embedding defines a modal operator (this Def.), on SuperFormalSmoothSet, which we denote by
Similarly, composing the projection which is the left Kan extension of the underlying bosonic space operation with the canonical re-embedding yields an endofunctor that has the interpretation of sending any generalized superspace to its underlying generalized bosonic space
In fact, since these two endofunctors are obtained from the two possible composites in an adjoint triple whose middle functor is fully faithful – corresponding to an adjoint modality (this Def.) – it is immediate to see that:
-
has the structure of a comodal operator
-
has the structure of an modal operator
-
together they form an adjoint modality .
Moreover, by prop. , this adjoint triple between and extends to an adjoint quadruple, there is yet one more endofunctor which is a further right adjoint idempotent comonad. Later we will see that this further opration is related to the concept of “rheonomy” in supergravity, and therefore we denote it by
But prop. says that there are yet further adjoints, however these no longer go between and , but between the former and or even just between the former and . For instance there is the composite projection
which first forms the bosonic underlying space, and then forms the reduced underlying space of what remains. The total result of this operation is just plain reduction, removing all infinitesimal directions, whether odd graded or even graded. Therefore, the result of composing this operation with its right adjoint canonical re-embedding yields an endofunctor which we should call
and think of as the operation of reduction on generalized super formal smooth sets.
Notice that reflective subcategory embeddings
are localizations, in that first including an object and then projecting it back to the subcategory is the identity operation ; and analogously for a coreflection (this prop.).
In our situation this first of all means that all of the endofunctors above are idempotent, as already mentioned. But next it implies that first applying a “deep” projection in the diagram in prop. , and then applying a “more shallow” projection with functors at the same vertical stage in the diagram does not change the result further. For example there is a natural isomorphism
saying that if a space is reduced, then it has no infinitesimal directions whatsoever, in particular no odd-graded ones, hence it is already bosonic.
We will denote this situation by an inclusion sign
to be read “reduced implies bosonic”. This is an example of the preorder on modalities (this Def.)
We may proceed this way with all the remaining functors in prop. , consecutively turning them into endofunctors on which are all related to each other by adjunctions or by this inclusion relation of projection operators.
The result is a system of 9 endofunctors, or 12 if we inclue the bottom adjoint modality and the top adjoint modality (this Example):
| shape modality | flat modality | sharp modality |
|---|---|---|
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
Proposition
(progression of adjoint modalities on SuperFormalSmoothSet)
We have a system of adjoint modalities (this Def.) and their preordering (this Def.) on SuperFormalSmoothSet (Def. ) that is induced (via this Prop.) by the system of adjoint functors in Prop. , as follows:
Moreover, the progression exhibits Aufhebung (this Def., this Remark) at each stage, as indicated.
Finally, the rheonomy modality is homotopy localization at (the superpoint) in the sense of this Def.:
Proof
The progression of modalities follows with Prop. by this Prop..
The right Aufhebung at the first stage says that , which means equivalently that for each SuperFormalCartSp we have
But by the adjunction hom-isomorphism (here) and the fact that (by the proof of this Prop.) and that we have indeed
The left Aufhebung at the third stage says that
This means equivalenty that for each and we have
Again by the adjunction isomorphisms we verify:
Here we used that on representables
which holds by direct inspection: it says that the odd-graded elements in a supercommutative superalgebra are all nilpotent.
Finally for the equivalence
the proof is directly analogous to that of the analogous statement in the chapter on smooth sets, this Prop:
As in that proof, the -local objects among all super formal smooth sets are equivalently those which are local objects with respect to the following small set of morphisms:
By induction over , these are equivalently the objects which are local with respect to the following small set:
But these are manifestly the objects which are in the image of :
Sometimes it is illuminating to re-arrange the diagram in Prop. equivalently as follows. Here we label each projection operator by the property of superspaces that it “projects out”.
Below we use these operations to identify within all generalized superspaces those that are supermanifolds. But first we consider now some general important constructions of super formal smooth sets, such as mapping spaces.
Super mapping spaces
We now discuss mapping spaces in supergeometry. These are interesting in two ways:
-
for the theory – mapping spaces nicely exhibit the usage and the power of the functor of points perspective (remark );
-
for applications – in physics a superfield is really a generalized element of a mapping space, and hence the phase spaces of interest in physics are mapping spaces (in the generality of spaces of spaces of sections, namely of a field bundle).
The key idea is that sets of functions between sets have the following universal property:
Example
Let Set be two sets, then the set
of functions from to is characterized by the fact that for any further set, there is a natural bijection
between functions of two variables into and functions of one variable into . This is given by sending any function of two variables to the function which sends any to the function . Hence this simply reinterprets “taking two arguments at once” by “taking two arguments consecutively”.
It is immediate how to generalize example :
Definition
Let be a category with Cartesian products of its objects, hence a cartesian monoidal category. Then an internal hom-functor for is, if it exists, a functor of the form
such that there is a natural bijection between hom sets of the form
for all objects .
The class of examples that we are interested in is the following:
Proposition
Let be a category of sheaves over some site .
Then the Cartesian product between any two sheaves exists and is given objectwise by the Cartesian product of sets:
for .
Moreover, an internal hom-functor according to def. exists (“generalized mapping space”). It sends any two sheaves to the sheaf
given by
where is the Yoneda embedding.
For the proof see at closed monoidal structure on presheaves.
Notice how prop. expresses an intuitively most obvious statement: Applied to geometric sheaf toposes such as SmoothSet or SuperFormalSmoothSet (def. ) it says that a -parameterized smooth family of points in a mapping space is a smooth map of the form , hence a family of smooth functions which is smoothly parameterized by .
The following shows formally that the concept of internal homs in the topos of generalized smooth spaces does generalize the traditional concept of smooth mapping spaces:
Example
Let be a compact smooth manifold and let be any smooth manifold. Then the set of smooth functions carries the structure of an infinite dimensional (in general) Fréchet manifold . Under the embedding of prop. this coincides with internal hom formed in according to prop. :
In particular for instance the smooth loop space of a smooth manifold is simply the internal hom .
A proof is given in Waldorf 09, lemma A.1.7.
But in the topos SuperFormalSmoothSet (def. ) we have also mapping spaces much more general than the traditional ones of example . We now look at some examples of these.
Example
Let
be the formal dual of the ring of dual numbers (example ). Observe that there is a unique morphism of the form , picking the base point.
Then for
a smooth manifold, regarded as a super formal smooth set (this Prop.ets#InclusionOfSmoothManifoldsIntoSmoothSets)), the internal hom out of with this basepoint is the smooth tangent bundle of (again under the embedding of this Prop.ets#InclusionOfSmoothManifoldsIntoSmoothSets)):
Proof
By prop. the rule for the smooth set is
By prop. , the set on the right is naturally identified with the set of of smoothly -parameterized families of tangent vectors in . But this is the set that , regarded as a smooth set, assigns to .
Moreover, looking at the proof of prop. it is immediate that composing a morphism
representing some tangent vector in with the global point inclusion of yields the point in
at which this tangent vector is based. This shows that the vertical map in the above claim is indeed the projection from the tangent bundle to the base manifold.
Example is a key observation that motivated the development of synthetic differential geometry (Lawvere 97).
The following is the supergeometric analog of this situation:
Example
(odd tangent bundle as mapping space)
Let be any smooth manifold. Then the internal hom in out of the superpoint into , according to prop. , is the odd tangent bundle from def. :
Proof
Let be a bosonic Cartesian space. By prop. the set of plots of the smooth set on this test space is
But since is bosonic (an ordinary smooth manifold), this is equivalently just
which shows that the bosonic super smooth set underlying is just itself.
But then consider probes parameterized by the superpoint :
where we used the adjunction from prop. , Prop. , then example and finally example .
Notice the curious difference between the bosonic and the odd-graded version of the synthetic tangent bundle as seen by its algebra of functions
In the first case the, smooth functions on the tangent bundle do not know about the linear structure on fibers. But in the second case, they do: the differential forms in the second case appear as the sub-space of that of all smooth functions on those which are graded polynomials (over the algebra of smooth functions on ) in fiber-wise linear functions.
More generally, this is the concept if superfields as used in the physics literature:
Example
Let be a supermanifold (for instance a super spacetime) and consider the super-mapping space (def. ) (or ) of real (or complex) valued functions on (“scalar fields”). We may understand the generalized elements of this superspace via its functor of points which, via prop. , is given by the assignment
Here in the first line on the right we have the set of maps of supermanifolds of the form , which, by the Yoneda lemma, is equivalently just the even subalgebra of the super-algebra of functions on , which finally is equivalently the even elements in the tensor product of the super-algebra of functions on with the Grassmann algebra on odd generators .
Now an element in this tensor product is of the form
for any and .
(Notice that here if is of superdimension , then this expansion becomes redundant for : The functor of points provides an arbitrary supply of auxiliary Grassmann coordinates , only some of which will typically be of non-redundant use for any given superspace.)
In physics, such a linear combination of even and odd component functions multipled with Grassmann algebra elements to yield a homogeneously graded sum is called a superfield.
In order to make sense of this, some physics textbooks (e.g. de Witt 92) posit a single “infinite dimensional Grassmann algebra” from which to draw the elements . This approach has its pitfalls Sachse 08, section 5.2. The functorial geometry perspective (remark ) fixes this: the “arbitrary supply” of Grassmann variables is encoded by saying that
-
for each finite dimensional Grassmann algebra superfields have an expansion in terms of the generators ;
-
these expressions are covariant with respect to change of Grassmann coordinates .
There are of course the evident generalizations of the scalar valued superfields along the same lines. In general there is a (super-)fiber bundle over (super) spacetime called the (super)-field bundle such that a field on is a section of the field bundle (see also at fiber bundles in physics). The super-space of sections of is the following fiber product of the mapping space
i.e. the super-space with the universal property that it makes the follwing square commute:
Then a superfield with values in is a generalized element of . By the functorial geometrythis means that field is over every superpoint a homomorphism such that
In a typical example is an ordinary smooth manifold with spin structure and is the odd version (according to example ) of a spinor bundle on .
Then an element of is
-
over no information;
-
over an element with an ordinary section of the spinor bundle (hence a spinor field).
and so on.
This may be combined: For example if is the direct sum of vector bundles of the trivial complex line bundle with an odd spinor bundle, then a generalized element of is over of the form
where is a complex-vaued scalar field and again a section of the spinor bundle.
This way bosonic fields and fermionic fields may be combined into a singe superfield (see also at super multiplet).
Supermanifolds
We now define and then discuss the analog of smooth manifolds in supergeometry – supermanifolds. In the spirit of the entire presentation, we do so by applying a general abstract definition of “V-manifold” or “-scheme” locally modeled on any given kind of model spaces to the special case where the local model spaces are super Cartesian spaces as discussed above. This general method is also discussed at geometry of physics – manifolds and orbifolds, but we recall the relevant points below.
Recall the adjoint pair of endofunctors
from Prop. . By prop. and prop. we know that sends a (formal) super Cartesian space to its underlying reduced ordinary Cartesian space. For instance
and generally
for any infinitesimally thickened superpoint.
This is enough to find what its right adjoint operation is doing:
Proposition
For (def. ), then is the super formal smooth set whose functor of points is given by
where and for any infinitesimally thickened superpoint.
Proof
By applying the Yoneda lemma, the natural bijection between hom-sets that characterizes the adjoint pair and using the characterization of we get the following sequence of natural isomorphisms:
Proposition means that for for instance an ordinary smooth manifold (regarded as a super formal smooth set via prop. ) then is a rather exotic kind of generalized smooth space: it has the same finite smooth curves and other finite smooth shapes as does, but every infinitesimal curve or shape inside it is necessarily constant. A good way to think about this (which is also the precise way to think about it, if we speak in the internal language of the sheaf topos) is that is the result obtained from by identifying all infinitesimally close points with each other. In algebraic geometry this construction is often known as forming the de Rham shape of (Simpson 96). Here we will say infinitesimal shape.
Another useful perspective on is the following:
Definition
For (def. ) then we say that its infinitesimal disk bundle is the left vertical morphism in the following pullback diagram
Moreover, for any global point of , then we say that the formal disk in at is the fiber of the infinitesimal disk bundle over that point
Definition
Given then a morphism is called a formally étale morphism if its naturality square of the infinitesimal shape modality (prop. )
is a pullback square.
We often indicate that a morphism satisfies this condition by labeling it “et” , hence
We unwind definition a little:
Remark
Let be an infinitesimally thickened point. This means that its reduction is the actual point, . By the adjunction from Prop. it follows that the image of the naturality square in def. under forming the internal hom (def. ) out of is
Since the internal hom preserves limits in its second argument (being right adjoint to ) this is a pullback square if is a formally étale morphism according to def. . In this form the condition appears in Yetter 88, def. 3.3.1.
If here we specify to be the formal dual of the ring of dual numbers, then , are the respective tangent bundles by example . Hence in this case the condition that is a formally étale morphism according to def. implies that the square
is a pullback square. For ordinary smooth manifolds via prop. , this condition is the traditional definition that be a local diffeomorphism.
Proposition
For two ordinary smooth manifolds via prop. , then a morphism between them is a formally étale morphism according to def. precisely if it is a local diffeomorphism in the traditional sense.
Proof
By remark the condition of def. on morphisms between smooth manifolds is equivalent to the traditional condition of being locally diffeo already when seen just under the internal hom out of .
But, as the name suggests, a local diffeomorphism of smooth manifolds is in particular also a local homeomorphism. This means that around each point of there is actually an open neighbourhood such that restricts to a diffeomorphism on that neighbourhood. This implies that the full condition in def. holds, by an argument as in example .
Example
For be given (def. ) and for any set, then the canonical morphism out of the coproduct (disjoint union) of copies of to itself is a local diffeomorphism according to def. :
Proof
Since is a left adjoint by prop. , Prop. , it preserves all colimits and hence in particular coproducts, hence the image of the morphism under is
Moreover, in any sheaf topos colimits are universal, which means that maps out of colimits are preserved under pullback. Moreover, the pullback of an isomorphism is an isomorphism, and so we deduce that we have a pullback diagram of the form
But, again because preserves colimits, this is manifestly the -naturality square of the original morphism.
Definition
Let be given (def. ), equipped with the structure of a group object.
A V-manifold is an such that there exists a -atlas, namely a correspondence of the form
with both morphisms being local diffeomorphisms, def. , and the right one in addition being an epimorphism.
By prop. this means that is in particular a V-manifold if there exists a set and a morphism out of the coproduct of copies of to which is a locally diffeomorphic epimorphism:
Specifically if be a super Cartesian space regarded as a group object under a translation supergroup action. Then we say that is a supermanifold of dimension if there exists
Remark
There are in general several translation supergroup structures carried by a super Cartesian space. For instance in the discussion at geometry of physics – supersymmetry we will consider super Minkowski supergroup structure which exists for special pairs . Just the existence of a supermanifold structure in def. does not depend on the choice of group structure on (and could be ignored for much of the present purpose). But later on the choice affects for instance the concept of torsion of a G-structure on the V-manifold.
Example
Let be a smooth manifold of dimension and a smooth vector bundle over of rank . Then there is a supermanifold (def. ) of dimension , denoted , as follows.
Write
for the supercommutative superalgebra which is the exterior algebra over of the -module of smooth sections (as in the smooth Serre-Swan theorem, Prop. ) of the dual vector bundle .
The underlying functor of points of (remark )
is the one that is represented by this algebra:
For instance if is the tangent bundle of , so that the dual bundle is the cotangent bundle, then
is the superalgebra of smooth differential forms on with respect to the wedge product, with any -form regarded as being in degree .
This is often called the odd tangent bundle.
Notice that generally we may think of as being the superspace which is obtained from the base manifold by adding an (odd-graded) infinitesimal thickening where an “infinitesimal step” away from some point is a vector in the fiber . This is particularly suggestive in the case that is the tangent bundle, because tangent vectors precisely want to be thought of as the infinitesimal paths in .
Below we see that this is not a coincidence, and discuss the formal proof that is the superspace of (odd-graded) infinitesimal paths in .
Proposition
(bosonic modality preserves formally étale morphisms)
If is a formally étale morphism, def. , then so is its image under the bosonic modality.
Proof
The first of these equivalences is the “left Aufhebung” which is explicit in Prop. . The second equivalence is under the Yoneda embedding, equivalent to the “adjunct equivalence”
which follows from the progression in Prop. since and have the same full subcategory of modal objects , and since , by (1).
Moreover, since preserves pullbacks (being a right adjoint, by this Prop.). Hence hitting a pullback diagram which exhibits a formally étale morphism (Def. )
with yields a pullback diagram
that witnesses as being formally étale morphisms formally étale.
Corollary
The bosonic space underlying a V-manifold , def. , is a -manifold.
Super differential forms
We discuss the super-geometric analog of differential forms on supermanifolds, first with coefficients in , then with coefficients in a super Lie algebra.
A super Cartesian space is the formal dual of the commutative superalgebra
in that a smooth function is equivalently (by definition!) a superalgebra homomorphism
Notice then that from knowledge of an algebra of functions one obtains the corresponding de Rham complex by the idea of Kähler differentials. As discussed there, this statement requires a little care in the smooth context, but the result is still immediate:
For a Cartesian space, then its de Rham complex is the -graded commutative dg-algebra whose underlying -graded vector space is
and whose differential is defined in degree-0 by
and extended from there to all degrees by the graded Leibniz rule.
It is immediate to generalize this to supergeometry, one just needs to be sure to apply the sign rule throughout.
Definition
(de Rham complex of super differential forms)
The de Rham complex of super differential forms on a super Cartesian space is the -bigraded commutative algebra
whose differential is defined in degree-0 by
and extended from there to all degree by the graded Leibniz rule.
Remark
We may write
for elements in this bigrading group.
In this notation the grading of the elements in is all induced by the fact that the de Rham differential itself is a derivation of degree .
| generator | bi-degree |
|---|---|
| (0,even) | |
| (0,odd) | |
| (1,even) |
Here the last line means that we have
| generator | bi-degree |
|---|---|
| (0,even) | |
| (0,odd) | |
| (1,even) | |
| (1,odd) |
The formula for the “cohomologically- and super-graded commutativity” in is
for all of homogeneous -degree. Hence there are two contributions to the sign picked up when exchanging two super-differential forms in the wedge product:
-
there is a “cohomological sign” which for commuting a -forms past an -form is ;
-
in addition there is a “super-grading” which for commuting a -graded coordinate function past a -graded coordinate function (possibly under the de Rham differential) is .
Example
See at signs in supergeometry for further discussion, for literature, and for mentioning of another popular sign convention, which is different but in the end yields the same cohomology.
We want to discuss the generalization of the concept of Lie algebra valued differential forms from ordinary differential geometry to supergeometry. To that end, we first recall the following neat formulation of ordinary Lie algebra valued differential forms due to Cartan. This will lend itself in fact not only to the generalization to super Lie algebras but further to super L-∞ algebras, which is what is needed for the description of higher dimensional supergravity.
Definition
The Chevalley-Eilenberg algebra of a finite dimensional Lie algebra is the semifree graded-commutative dg-algebra whose underlying graded algebra is the Grassmann algebra
(with the th skew-symmetrized power in degree )
and whose differential (of degree +1) is on the dual of the Lie bracket
extended uniquely as a graded derivation on .
That this differential indeed squares to 0, , is precisely the fact that the Lie bracket satisfies the Jacobi identity.
Remark
If in the situation of prop. we choose a dual basis of and let be the structure constants of the Lie bracket in that basis, then the action of the differential on the basis generators is
where here and in the following a sum over repeated indices is implicit.
Proposition
The construction of Chevalley-Eilenberg algebras in def. yields a fully faithful functor
embedding Lie algebras into formal duals of differential graded algebras. Its image consists of precisely of the semifree dg-algebras, those whose underlying graded algebra (forgetting the differential) is a Grassmann algebra generated on a vector space.
Definition
Given a Lie algebra , its Weil algebra is the semi-free dga whose underlying graded-commutative algebra is the exterior algebra
on and a shifted copy of , and whose differential is the sum
of two graded derivations of degree +1 defined by
-
acts by degree shift on elements in and by 0 on elements of ;
-
acts on unshifted elements in as the differential of the Chevalley-Eilenberg algebra of and is extended uniquely to shifted generators by graded-commutattivity
with :
for all .
Proposition
Given a Lie algebra , then a Lie algebra valued differential form on, say, a Cartesian space , is equivalently a dg-algebra homomorphims
hence there is a natural bijection
The form is flat in that its curvature differential 2-form vanishes, precisely if this morphism factors through the CE-algebra.
Remark
With a choice of basis as in remark , then the content of prop. is seen in components as follows:
a dg-algebra homomorphism is first of all a homomorphism of graded algebras, and since the domain is free as a graded algebra, such is entirely determined by what it does to the generators
But being a dg-algebra homomorphism, this assignment needs to respect the differentials on both sides. For the original generators this gives
With this satisfied, then, by the very nature of the Weil algebra, the differential is automatically respected also on the shifted generators. This statement is the Bianchi identity.
Now to pass this to superalgebra.
Definition
For a super vector space, then its Grassmann algebra is the free -bigraded commutative algebra subject to
In the spirit of prop. we may then simply say that:
Definition
A super Lie algebra structure on a super vector space is the formal dual of a -bigraded commutative differential algebra
(with differential of degree (1,even)) such that the underlying graded algebra is the super Grassmann algebra via def. .
We call this again the Chevalley-Eilenberg algebra of the super Lie algebra dually defined thereby.
Similarly, the Weil algebra is obtained from this by adding a generator in degree for each previous generator in degree and extending the differential as in def. .
Unwinding what this means, one finds that it is equivalent to the following more traditional definition:
Proposition
A super Lie algebra is equivalently
-
equipped with a bilinear bracket
which is graded skew-symmetric: for two elements of homogeneous degree , , respectively, then
-
that satisfies the -graded Jacobi identity in that for any three elements of homogeneous super-degree then
But with def. we immediately known, in view of prop. , what super Lie algebra valued super differential forms should be:
Definition
Given a super Lie algebra , def. , prop. , then a -valued super-differential form on the super Cartesian space is a -graded dg-algebra homomorphism
from the Weil algebra according to def. , to the super de Rham complex of def. .
Accordingly we write
Example
Let be the ordinary abelian line Lie algebra. Then
is the set of super-differential forms in degree .
Similarly with the odd line regarded as an abelian super Lie algebra, then
So generally for an ordinary Lie algebra regarded as a super Lie algebra, then is bigger than .
This is an issue to be dealt with when describing supergravity in terms of Cartan fields on supermanifolds , because the actual spacetime manifold one cares about is just the bosonic part . This issue is dealt with by the concept of rheonomy.
References
General theory
Some historically influential remarks on supergeometry are due to
- Yuri Manin, New Dimensions in Geometry, talk at Arbeitstagung, Bonn 1984
Introductory lecture notes include
-
Yuri Manin, chapter 4 of Gauge Field Theory and Complex Geometry, Grundlehren der Mathematischen Wissenschaften 289, Springer 1988
-
Gennadi Sardanashvily, Lectures on supergeometry (arXiv:0910.0092)
Many texts discuss supergeometry only in the context of supersymmetry, but notice that the former exists and is relevant even if the latter does not or is not.
-
L. Caston, R. Fioresi, Mathematical Foundations of Supersymmetry (arXiv:0710.5742)
For classical field theories with fermions
The experimental observation that phase spaces of classical field theories with fermions (such as electrons or quarks) are superspaces goes back to
-
Wolfgang Pauli, Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren, Zeitschrift für Physik, February 1925, Volume 31, Issue 1, pp 765-783
-
Markus Fierz, Über die relativistische Theorie kräftefreier Teilchen mit beliebigem Spin. Helvetica Physica Acta. 12 (1): 3–37. (1939) doi:10.5169/seals-110930
-
Wolfgang Pauli, The connection between spin and statistics, Phys. Rev. 58, 716–722 (1940)
Discussion of classical field theory with fermions as taking place on supermanifolds (supergometric field bundles and phase space) includes the following references:
-
Pierre Deligne, Daniel Freed, Classical field theory (1999) (pdf)
this is a chapter in
P. Deligne, P. Etingof, D.S. Freed, L. Jeffrey, D. Kazhdan, J. Morgan, D.R. Morrison, E. Witten (eds.) Quantum Fields and Strings, A course for mathematicians, 2 vols. Amer. Math. Soc. Providence 1999. (web version)
-
Daniel Freed, Classical field theory and Supersymmetry, IAS/Park City Mathematics Series Volume 11 (2001) (pdf)
-
Giovanni Giachetta, Luigi Mangiarotti, Gennadi Sardanashvily, chapter 3 of Advanced classical field theory, World Scientific (2009)
-
Gennadi Sardanashvily, Grassmann-graded Lagrangian theory of even and odd variables (arXiv:1206.2508)
-
Gennadi Sardanashvily, Noether’s Theorems: Applications in Mechanics and Field Theory, Studies in Variational Geometry, 2016
In the topos over superpoints
The observation that the study of super-structures in mathematics is usefully regarded as taking place over the base topos on the site of super points has been made around 1984 in
-
Albert Schwarz, On the definition of superspace, Teoret. Mat. Fiz. (1984) Volume 60, Number 1, Pages 37–42, (russian original pdf)
-
Alexander Voronov, Maps of supermanifolds , Teoret. Mat. Fiz. (1984) Volume 60, Number 1, Pages 43–48
and in
- V. Molotkov., Infinite-dimensional -supermanifolds , ICTP preprints, IC/84/183, 1984.
A summary/review is in the appendix of
-
Anatoly Konechny and Albert Schwarz,
On -dimensional supermanifolds in Julius Wess, V. Akulov (eds.) Supersymmetry and Quantum Field Theory (D. Volkov memorial volume) Springer-Verlag, 1998, Lecture Notes in Physics, 509 , (arXiv:hep-th/9706003)
Theory of -dimensional supermanifolds Sel. math., New ser. 6 (2000) 471 - 486
-
Albert Schwarz, I- Shapiro, Supergeometry and Arithmetic Geometry (arXiv:hep-th/0605119)
A review of all this as geometry in the topos over the category of superpoints is in
- Christoph Sachse, A Categorical Formulation of Superalgebra and Supergeometry (arXiv:0802.4067)
In the topos over super Cartesian spaces
The above perspective of supergeometry in the topos over superpoints is a restriction of the perspective in the topos over super Cartesian spaces which we use here. This in turn is essentially just the specification to supercommutative superalgebra of Alexander Grothendieck‘s concept of “functorial geometry” as laid out in
- Alexander Grothendieck, Introduction au langage fonctoriel, course in Algiers in November 1965, lecture notes by Max Karoubi, pdf scan.
Grothendieck amplified that this functorial perspective is superior to the perspective on schemes as locally ringed spaces in the lecture
- Alexander Grothendieck, Introduction to functorial algebraic geometry, part 1: affine algebraic geometry, summer school in Buffalo, 1973, lecture notes by Federico Gaeta (pdf scan)
Further amplification of Grothendieck’s amplification may be found in the short text
- William Lawvere, Grothendieck’s 1973 Buffalo Colloquium, posting to the mailing list categories@mta.ca, March 2003 (gmane archive)
The application of this perspective to supergeometry is sometimes known as synthetic differential supergeometry:
- David Yetter, Models for synthetic supergeometry, Cahiers, 29, 2 (1988) (NUMDAM)
The formulation via the axioms of differential cohesion that we use here follows
-
Hisham Sati, Urs Schreiber, Sec. 3.1.3 of: Proper Orbifold Cohomology (arXiv:2008.01101)
-
Igor Khavkine, Urs Schreiber, Synthetic geometry of differential equations Part I – Jets and comonad structure (arXiv:1701.06238)
-
Felix Wellen, Formalizing Cartan Geometry in Modal Homotopy Type Theory, 2017 (arXiv:1806.05966, pdf)
Last revised on October 12, 2023 at 14:10:45. See the history of this page for a list of all contributions to it.
