Schreiber Cyclification of Orbifolds
An article that we have written:
-
Cyclification of Orbifolds
Comm. Math. Phys. 405 67 (2024)
doi:10.1007/s00220-023-04929-w
download:
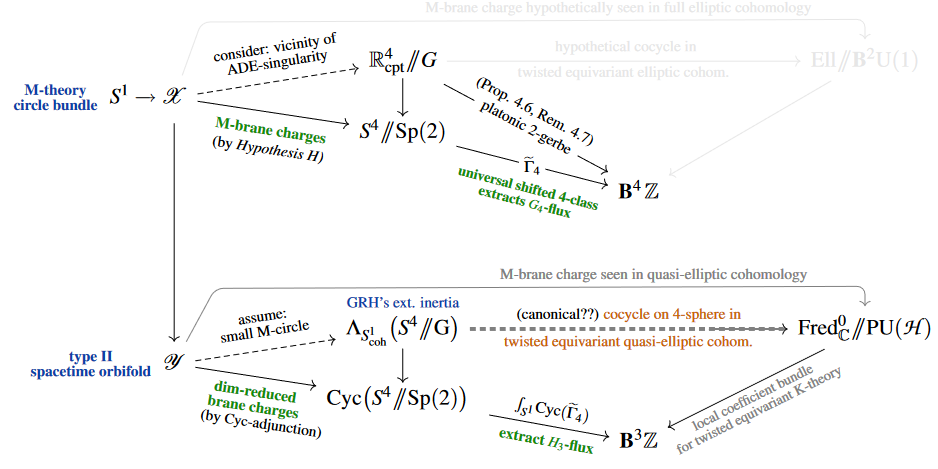
Abstract. Inertia orbifolds homotopy-quotiented by rotation of geometric loops play a fundamental role not only in ordinary cyclic cohomology, but more recently in constructions of equivariant quasi-elliptic cohomology and generally of transchromatic characters on generalized cohomology theories. Nevertheless, existing discussion of such cyclified stacks has been relying on ad-hoc component presentations with intransparent and unverified stacky homotopy type.
Following our previous formulation of transgression of cohomological charges (“double dimensional reduction”), we explain how cyclification of -stacks is a fundamental and elementary base change construction over moduli stacks in cohesive higher topos theory (cohesive homotopy type theory). We prove that Ganter-Huan's extended inertia groupoid used to define equivariant quasi-elliptic cohomology is indeed a model for this intrinsically defined cyclification of orbifolds, and we show that cyclification implements transgression in group cohomology in general, and hence in particular the transgression of degree-4 twists of equivariant quasi-elliptic cohomology to degree-3 twists of orbifold K-theory on the cyclified orbifold.
As an application, we show that the universal shifted integral 4-class of equivariant 4-Cohomotopy theory on ADE-orbifolds induces the Platonic 4-twist of ADE-equivariant quasi-elliptic cohomology; and we close by explaining how this should relate to elliptic genera of the M5-brane, under our previously formulated Hypothesis H.
Related articles:
-
T-Duality from super Lie n-algebra cocycles for super p-branes
-
Gauge enhancement of super M-branes via parametrized stable homotopy theory
Related talks:
-
Cyclic loop spaces via higher topos theory in high energy physics,
talk at: Loop spaces and Higher categories,
HUST & SCUT (2-3 Dec 2022)
-
Introduction to Higher Supergeometry
at Higher Structures in M-Theory 2018
Durham, Aug 2018
-
at Conf. on Duality in Homotopy theory
Regensburg, April 2017
-
Super Lie -algebra of Super -branes
at Fields, Strings, and Geometry Seminar
Surrey, Dec 2016
Last revised on February 27, 2024 at 06:58:42. See the history of this page for a list of all contributions to it.