Schreiber Gauge enhancement of Super M-Branes
An article that we have written:
-
Vincent Braunack-Mayer, Hisham Sati, Urs Schreiber:
Gauge enhancement of Super M-Branes
via rational parameterized stable homotopy theoryCommunications in Mathematical Physics
371 (2019) 197–265
download article at:
doi:10.1007/s00220-019-03441-4
download exposition at:
Abstract:
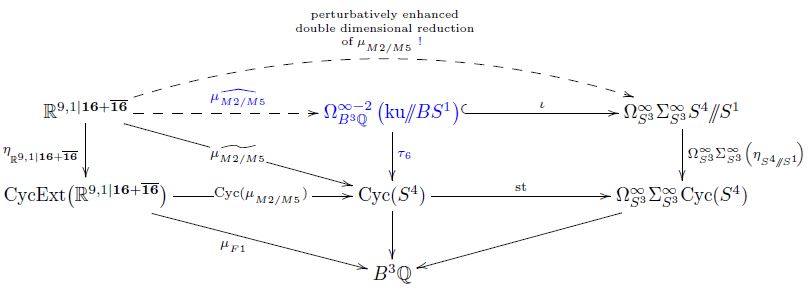
A key open problem in M-theory is the mechanism of “gauge enhancement”, which supposedly makes M-branes exhibit the nonabelian gauge degrees of freedom that are seen perturbatively in the limit of 10d string theory. In fact, since only the twisted K-theory classes represented by nonabelian Chan-Paton gauge fields on D-branes have invariant meaning, the problem is really the lift to M-theory of the twisted K-theory classification of D-brane charges.
Here we show how this problem has a solution by universal constructions in super homotopy theory, at least rationally. We recall how double dimensional reduction of super M-brane charges is described by the cyclification adjunction applied to the 4-sphere, and how M-theory degrees of freedom hidden at ADE-singularities are induced by the suspended Hopf action on the 4-sphere. Combining these, we demonstrate, at the level of rational homotopy theory, that gauge enhancement in M-theory is exhibited by lifting against the fiberwise stabilization of the unit of this cyclification adjunction on the A-type orbispace of the 4-sphere.
Related talks:
-
talk at StringMath2017 (download: pdf)
-
presentation at Strings2019 (download: pdf)
Based on:
-
Rational parameterized stable homotopy theory
thesis, Zurich 2018
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
The rational higher structure of M-theory
Proceedings of the LMS-EPSRC Durham Symposium:
Higher Structures in M-Theory, August 2018
Fortschritte der Physik, 2019
summarizing:
Followups:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber:
-
Equivariant Cohomotopy implies orientifold tadpole cancellation
Last revised on December 9, 2023 at 19:28:53. See the history of this page for a list of all contributions to it.