nLab AdS-CFT correspondence
Context
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Quantum field theory
Contents
- Idea
- Polyakov gauge/string duality
- Checks
- Examples
- – Horizon limit of D3-branes
- – Horizon limit of M5-branes
- –Horizon limit of M2-branes
- – Horizon limit of D-D() brane bound states
- Non-conformal duals
- Further gauge theories induced by compactification and twisting
- Formalizations
- Related concepts
- References
- Polyakov gauge/string duality
- Microscopic AdS/CFT via -brane sigma-models
- The origin of modern AdS/CFT duality
- Introductions and surveys
- Lattice gauge theory computations
- On single trace operators
- SYK-model in
- Random matrix theory in
- BFSS matrix model in
- Flat space limit
- D1-D3 brane intersections in
- Chord diagrams and weight systems in Physics
- In Chern-Simons theory
- For single trace operators in AdS/CFT duality
- In , JT-gravity/SYK-model
- In D/D-brane intersections
- As codes for holographic entanglement entropy
- For Dyson-Schwinger equations
- Other
- On
- On
- On
- On
- Generalization beyond exact AdS / exact CFT
- pp-Waves as Penrose limits of spacetimes
- Applications to physics
- To gravity
- To the quark-gluon plasma
- To particle physics
- To fluid dynamics
- To condensed matter physics
- Applications in mathematics
- Philosophy of AdS/CFT
Idea
General idea
The AdS-CFT correspondence at its heart is the observation (Witten 98, Section 2.4) that the classical action functionals for various fields coupled to Einstein gravity on anti de Sitter spacetime are, when expressed as functions of the asymptotic boundary-values of the fields, of the form of generating functions for correlators/n-point functions of a conformal field theory on that asymptotic boundary, in a large N limit.
This is traditionally interpreted as a concrete realization of a vague “holographic principle” according to which quantum gravity in bulk spacetimes is controlled, in one way or other, by “boundary field theories” on effective spacetime boundaries, such as event horizons. The original and main motivation for the holographic principle itself was the fact that the apparent black hole entropy in Einstein gravity scales with the area of the event horizon instead of the black hole’s bulk volume (which is not even well-defined), suggesting that gravity encodes or is encoded by some boundary field theory associated with horizons; an idea that, in turn, seems to find a concrete realization in open/closed string duality in the vicinity of, more generally, black branes. The original intuition about holographic black hole entropy has meanwhile found remarkably detailed reflection in the (mathematically fairly rigorous) analysis of holographic entanglement entropy, specifically via holographic tensor networks, which turn out to embody key principles of the AdS/CFT correspondence in the guise of quantum information theory, with concrete applications such as to quantum error correcting codes.
The AdS/CFT correspondence itself crucially involves the exceptional isomorphism between the isometry group of anti de Sitter spacetime (the anti de Sitter group) and the conformal group of Minkowski spacetime of dimension : the connected component of both is the special orthogonal group . But the AdS/CFT correspondence is deeper and more subtle than this group theory underlying it, in particular in how it puts fields and states on the gravity side in correspondence with sources and correlators on the field theory side, respectively.
In extrapolation of these elementary computations, the AdS/CFT correspondence conjecturally extends to a more general identification of states of gravity (quantum gravity) on asymptotically anti de Sitter spacetimes of dimension with correlators/n-point functions of conformal field theories on the asymptotic boundary of dimension (Gubser-Klebanov-Polyakov 98 (12), Witten 98, (2.11)), such that perturbation theory on one side of the correspondence relates to non-perturbation on the other side.
While this works to some extent quite generally (see e.g. Natsuume 15 for review), allowing applications such as AdS/CFT in condensed matter physics and AdS/CFT in quantum chromodynamics, the tightest form of the correspondence relates the 1/N expansion of superconformal field theories (super Yang-Mills theories) on the asymptotic boundaries of near-horizon limits of coincident black M2-branes/D3-branes/M5-branes to corresponding sectors of the string theory/M-theory quantum gravity in the bulk spacetime away from the brane.
Before the proposal for the actual matching rule of ADS/CFT (Gubser-Klebanov-Polyakov 98 (12), Witten 98, (2.11)) it was by matching of BPS-states in these situations that the existence of an AdS/CFT correspondence was proposed in Maldacena 97a, Maldacena 97b; these articles are now widely regarded as the origin of the idea of the AdS/CFT correspondence.
A quick way to see that the supersymmetric-cases of AdS/CFT for near horizon geometries of M2-branes, D3-branes and M5-branes must be special is to observe that these are the only dimensions in which there are super anti-de Sitter spacetime-enhancements of anti de Sitter spacetime, matching the classification of simple superconformal symmetries, see there:
(Shnider 88, also Nahm 78, see Minwalla 98, section 4.2)
It had already been observed by Bergshoeff, Duff, Pope & Sezgin and Duff & Sutton 1988 (see also Duff 1998, Duff 1999) that the field theory of small perturbation of a Green-Schwarz sigma-model for a fundamental brane stretched over the asymptotic boundary of the AdS near horizon geometry of its own black brane-incarnation is, after diffeomorphism gauge fixing, a conformal field theory. This was further developed in Claus, Kallosh & Proeyen 1997, DGGGTT 98, Claus-Kallosh, Kumar & Townsend 1998, Pasti, Sorokin & Tonin 1999. See also at super p-brane – As part of the AdS-CFT correspondence
More recently, for the archetypical case of AdS/CFT relating N=4 D=4 super Yang-Mills theory to type IIB string theory on super anti-de Sitter spacetime , fine detailed checks of the correspondence have been performed (Beisert et al. 10, Escobedo 12), see the section Checks below.
Thus regarded as a duality in string theory, the AdS/CFT correspondence is an incarnation of open/closed string duality, reflecting the fact that the physics on D-branes has two equivalent descriptions:
1) as a Yang-Mills-gauge theory coming from open strings attached to the brane
2) as a gravity theory coming from closed strings emitted/absorbed by the brane.
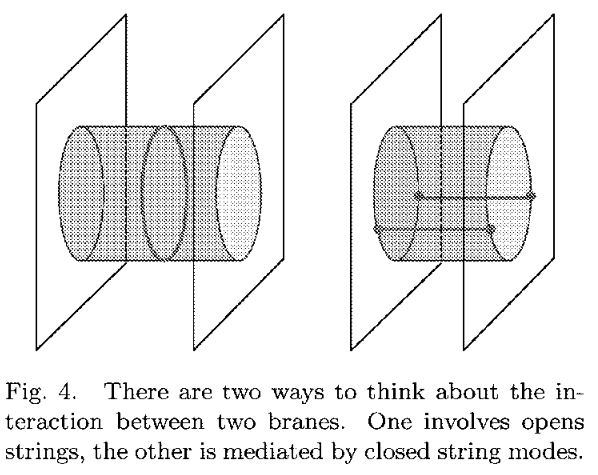
graphics grabbed from Schomerus 07, Figure 4, see also e.g. Peschanskia 09, Figure 1
This gives a vivid intuitive picture of the mechanism underlying the correspondence: An excitation of the gauge field on the brane goes along with an excitation of the field of gravity around the brane, and either is faithfully reflected in the other; at least in the suitable limits.
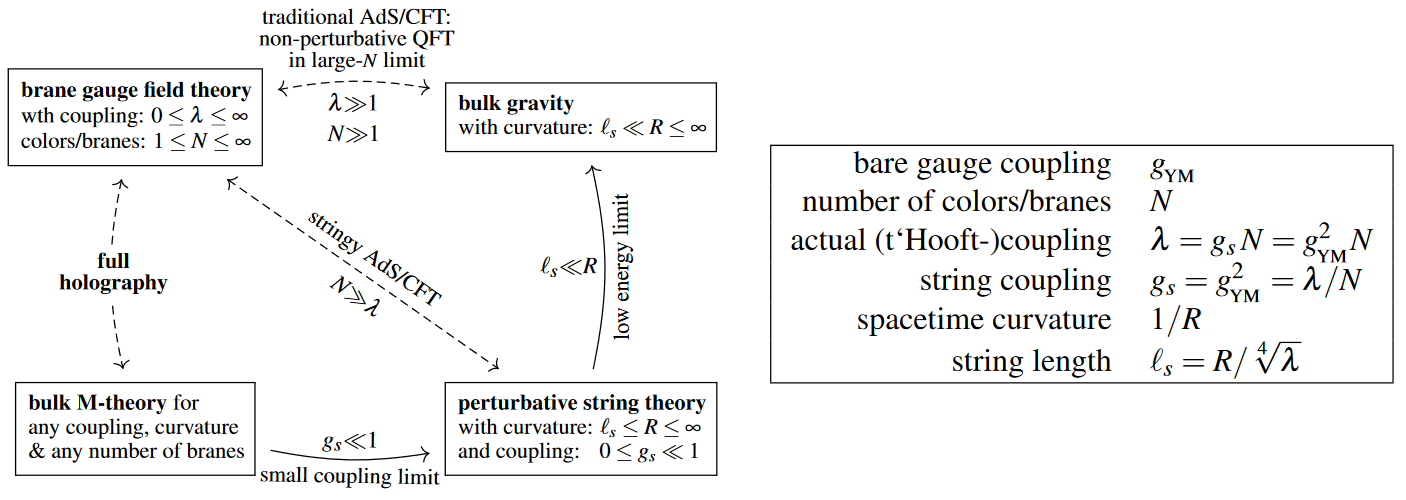
Small- corrections
The AdS/CFT correspondence has been widely discussed and is mostly understood by default only in the large limit and for large 't Hooft coupling, where the given gauge theory is dual to plain classical supergravity, which stands out as being particularly tractable and well-understood.
But it is expected (cf. AGMOO99 p. 60, Chester 2018, Chester & Perlmutter 2018 p. 2) that the duality still applies in the opposite large 1/N limit, now involving on the gravity-side corrections
-
from perturbative string theory (for small 't Hooft coupling, there are some checks of such stringy corrections) and
-
from putative M-theory (for the full non-perturbative large 1/N limit, which remains largely unexplored):
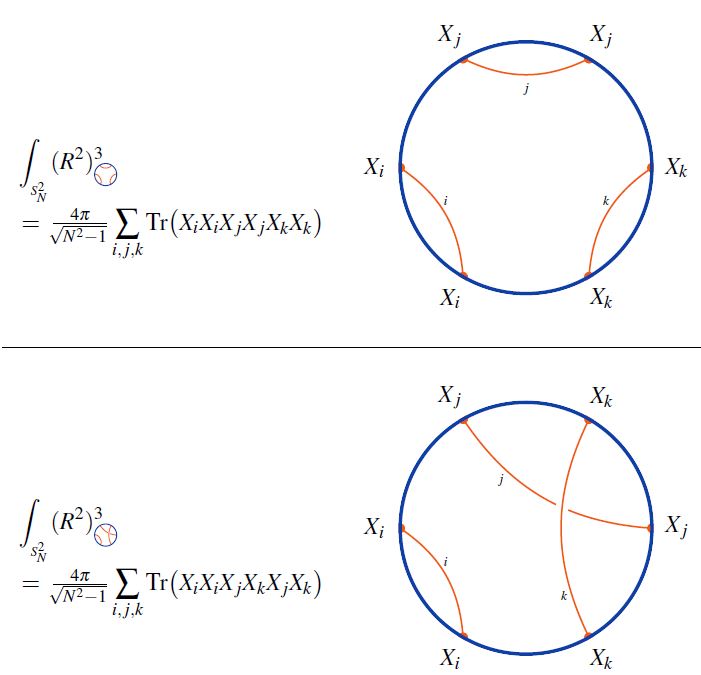
(graphics adapted from SS22)
Notice that for real-world applications such as to the confinement/mass gap-problem of quantum chromodynamics, the value of typically is indeed small (the number of colors in quantum chromodynamics is ) so that the string theory/M-theory-corrections to the AdS/QCD correspondence are going to be crucial for the full discussion of these applications:
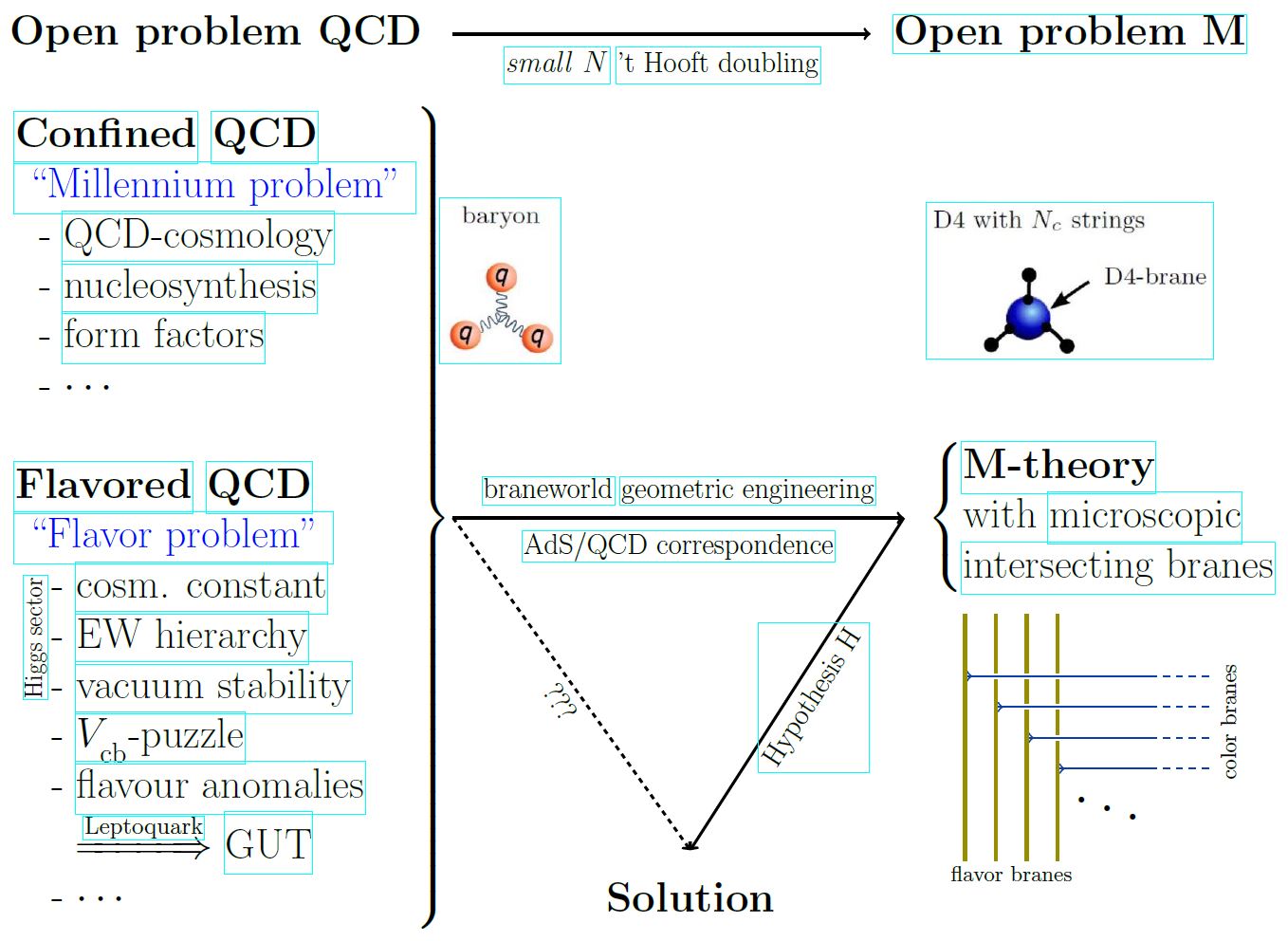
In lack of a full formulation of M-theory (see M-theory – The open problem) approximate forms of the AdS/CFT correspondence away from the case of conformal invariance, supersymmetry, large N limit and/or exact anti de Sitter geometry are being argued to be of use for understanding quantum chromodynamics (for instance the quark-gluon plasma (Policastro-Son-Starinets 01, but most notably confined hadron-spectra – the AdS/QCD correspondence) and for various models in solid state physics (the AdS-CFT in condensed matter physics, see e.g. Hartnoll-Lucas-Sachdev 16).
More in detail, since the near horizon geometry of BPS black branes is conformal to the Cartesian product of anti de Sitter spaces with the unit -sphere around the brane, the cosmology of intersecting D-brane models realizes the observable universe on the asymptotic boundary of an approximately anti de Sitter spacetime (see for instance Kaloper 04, Flachi-Minamitsuji 09). The basic structure is hence that of Randall-Sundrum models, but details differ, such as notably in warped throat geometries, see Uranga 05, section 18.
These warped throat models go back to Klebanov-Strassler 00 which discusses aspects of confinement in Yang-Mills theory on conincident ordinary and fractional D3-branes at the singularity of a warped conifold. See also Klebanov-Witten 98
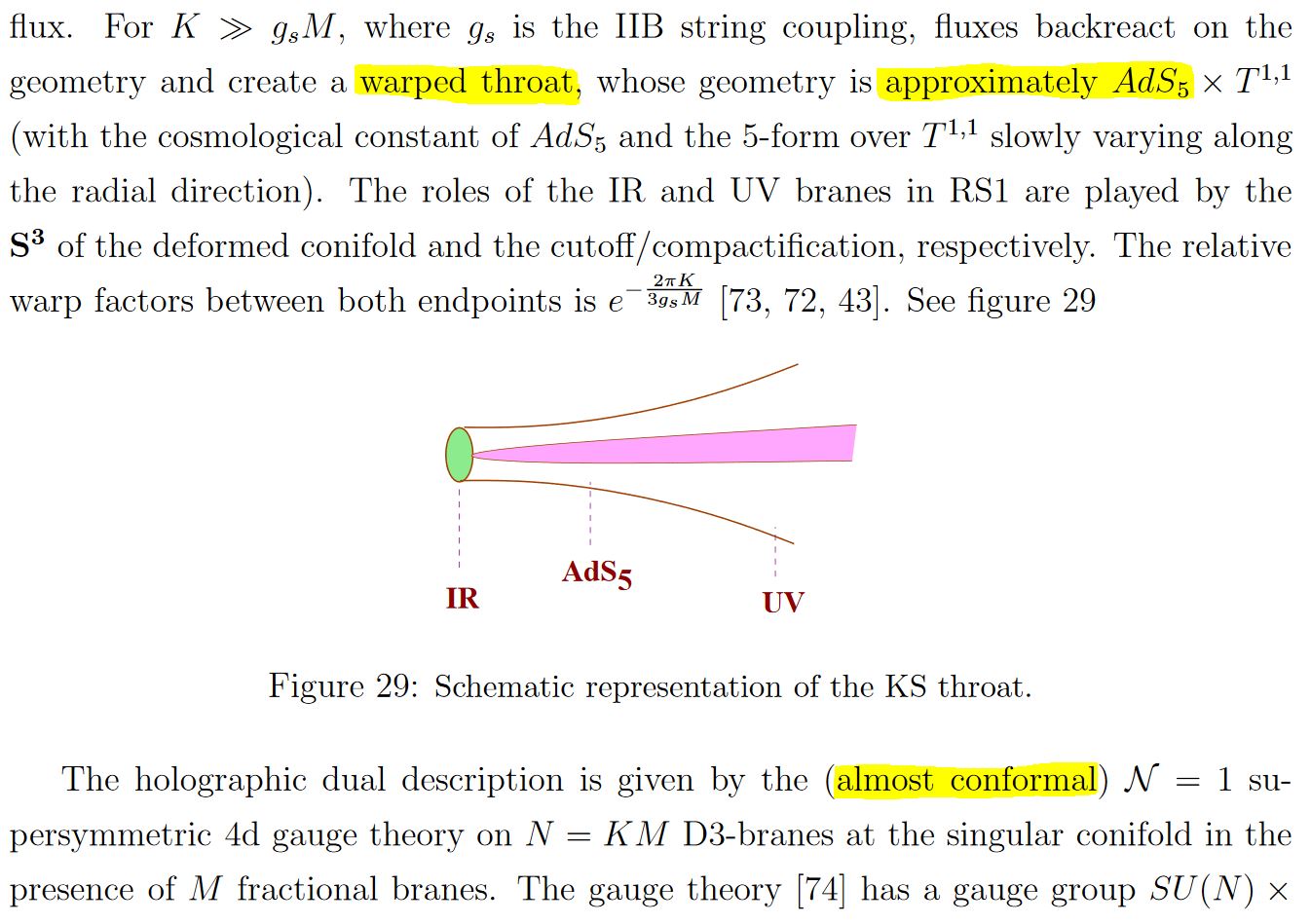
snippet grabbed from Uranga 05, section 18
here: “RS”=Randall-Sundrum model; “KS”=Klebanov-Strassler 00
In particular this means that AdS-CFT duality applies in some approximation to intersecting D-brane models (e.g. Soda 10, GHMO 16), thus allowing to compute, to some approximation, non-perturbative effects in the Yang-Mills theory on the intersecting branes in terms of gravity on the ambient warped throat AdS (Klebanov-Strassler 00, section 6)
Matching single trace observables to string excitation
The single trace operators/observables in conformal field theories such as super Yang-Mills theories play a special role in the AdS-CFT correspondence: They correspond to single string excitations on the AdS-supergravity side of the correspondence, where, curiously, the “string of characters/letters” in the argument of the trace gets literally mapped to a superstring in spacetime (see the references below).
From Polyakov 02, referring to gauge fields and their single trace operators as letter and words, respectively:
The picture which slowly arises from the above considerations is that of the space-time gradually disappearing in the regions of large curvature. The natural description in this case is provided by a gauge theory in which the basic objects are the texts formed from the gauge-invariant words. The theory provides us with the expectation values assigned to the various texts, words and sentences.
These expectation values can be calculated either from the gauge theory or from the strongly coupled 2d sigma model. The coupling in this model is proportional to the target space curvature. This target space can be interpreted as a usual continuous space-time only when the curvature is small. As we increase the coupling, this interpretation becomes more and more fuzzy and finally completely meaningless.
From Berenstein-Maldacena-Nastase 02, who write for the elementary field observables (“letters”) above:
In summary, the “string of s” becomes the physical string and that each carries one unit of which is one unit of . Locality along the worldsheet of the string comes from the fact that planar diagrams allow only contractions of neighboring operators. So the Yang Mills theory gives a string bit model where each bit is a operator.
On the CFT side these BMN operators of fixed length (of “letters”) are usefully identified as spin chains which, with the dilatation operator regarded as their Hamiltonian, are integrable systems (Minahan-Zarembo 02, Beisert-Staudacher 03).
This integrability allows a detailed matching between
-
single trace operators/BMN operators in D=4 N=4 super Yang-Mills theory
-
the classical Green-Schwarz superstring on AdS5 S5
under AdS/CFT duality (Beisert-Frolov-Staudacher-Tseytlin 03, …). For review see BBGK 04, Beisert et al. 10.
(…)
Polyakov gauge/string duality
Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical reminiscences in Polyakov (2008)) under the name gauge/string duality, in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings.
The logic here proceeds in the following steps (cf. Polyakov (2007), §1 and see the commentary below):
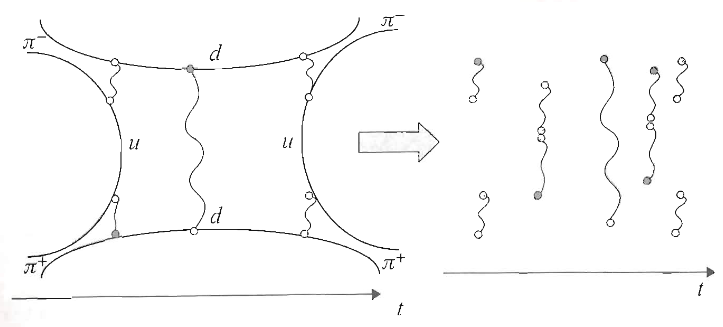
-
flux tubes confine as dynamical strings
The starting point is the hypothesis that the strong coupling of particles (such as quarks) by a (non-abelian) gauge field (such as the strong nuclear force) is embodied by the formation of “flux tubes” (“Wilson lines”) between pairs of such particles, which in themselves behave like strings with a given tension.
Kogut & Susskind (1974), (1975); Wilson (1974); Polyakov (1979), (1980), (1987); Makeenko & Migdal (1981), following Nambu (1970), Gotō (1971)
Under this assumption it would be:
-
the flux tube/string‘s tension which keeps the particles at theirs endpoints confined,
-
the excitation of these flux tubes/strings which follow Regge trajectories (such as of hadrons);
-
the scattering of these flux tubes/strings which explains the observed Veneziano amplitudes,
which are the main qualitative features to be explained.
-
-
quantum flux tubes probe effective higher dimensions
But if so, famous quantum effects make such flux tubes/strings behave like propagating in an effective/emergent higher-dimensional spacetime:
- either because one regards the string as a priori propagating in non-critical spacetime-dimension , in which case the dilaton field/Liouville field appears to cancel the quantum anomaly and acts like a warped 5th dimension:
this was the point of view published in Polyakov (1981) but later claimed, in Polyakov (2008), to have originated already “by the end of ‘77”;
- or because one regards the string as propagating in critical dimension (10 for the superstring) right away,
which is the point of view adopted later in AdS-CFT duality, starting with Maldacena (1997)
with only the endpoints of the flux tube/string constrained to lie in the original lower dimensional spacetime
which now appears (in modern language that Polyakov did not originally use) as a “brane” inside a higher dimensional bulk spacetime.
Notice that in this picture the observable physics that we set out to describe takes place on the brane (underlying which is typically flat Minkowski spacetime!) at the asymptotic boundary of a higher-dimensional bulk spacetime, while the (potentially large) extra dimensions of a possibly AdS-bulk remain primarily unobservable. In fact, in Polyakov’s original picture the extra 5th dimension is not so much a spacetime dimension but a parameter for the thickness of the flux tube, which becomes non-vanishing due to quantum effects cf. Polyakov (2008), p. 3.
-
large/small confined gauge theory is holographic string theory/M-theory
Thus the description of strongly coupled matter via flux tubes/strings now reveals a holographic situation where strongly-coupled quantum fields on intersecting branes are equivalently described by a theory of quantum gravity mediated by strings propagating in a higher dimensional bulk spacetime.
In relation to gauge string duality this is due to Gubser, Klebanov & Polyakov (1998), which is now understood as part of AdS/CFT duality, but it is actually meant to be more general, cf. Polyakov & Rychkov (2000).
While this dual bulk string theory is itself strongly-coupled unless the “number of coincident branes” is humongous (the “large-N limit”) and thus unrealistic after all, the difference is that recognizing the branes as physical objects reveals a web of concrete hints as to the string’s strongly-coupled (non-perturbative) completion, going under the working title M-theory, cf. at AdS-CFT – Small corrections.
In summary, the plausible approach of understanding strongly-coupled quantum gauge theories by regarding their flux tubes as dynamical strings seems to recast the Millennium Problem of understanding strongly-coupled matter into the problem of formulating M-theory: Given M-theory, it ought to be possible to find intersecting brane models of single (or a small number of coincident) M-branes (such as the Witten-Sakai-Sugimoto model M5-brane system) on whose worldvolume the desired strongly-coupled field theory is realized (such as QCD).
Notice the decisive early insight of Alexander Polyakov here: While the idea that strings somehow describe hadronic bound states was the very origin of string theory in the early 1970s (“dual resonance models”), the mainstream abandoned this perspective in the later 1970s when the critical dimension and the full spectrum of the string became fully understood (cf. Goddard-Thorn no-ghost theorem) and declared that instead string should be understood as a grand unified theory of everything including quantum gravity (see e.g. the historical review of Veneziano (2012), esp. pp. 30-31 which still clings to this perspective). From here it was only through the long detour of first discovering, inside this grander theory: D-branes (and M5-branes) in the 1990s, then their near-horizon AdS-CFT duality just before the 2000s and then another decade of exploring intersecting D-brane models that the community in the 2010s came back full circle to Polyakov’s holographic perspective on QCD, now dubbed holographic QCD, in which strings are flux tubes that propagate not (alone) in the observable 4 spacetime dimensions but in a primarily unobservable (meanwhile known as Randall-Sundrum-like) higher-dimensional bulk spacetime – a holographic description of reality that Polyakov (1999) referred to as the wall of the cave, in allusion to Plato (cf. also Polyakov (2008), p. 6).
Our whereabouts in this remarkable picture are still often misunderstood today: If string theory is a theory of nature, then, it seems, we see the wall but not the cave: we live on a Minkowskian brane intersection at the (asympotic) boundary of a primarily unobserved anti de Sitter bulk – which may better be thought of not as physical space but as a configuration space of quantum flux.
Checks
At the heart of the duality is the observation that the classical action functionals for various fields coupled to Einstein gravity on anti de Sitter spacetime are, when expressed as functions of the asymptotic boundary values of the fields, equal to the generating functions for the correlators/n-point functions of a conformal field theory on that asymptotic boundary.
These computations were laid out in Witten 98, section 2.4 “Some sample computation”. These follow from elementary manipulation in differential geometry (involving neither supersymmetry nor string theory). A good exposition is in Hartnoll-Lucas-Sachdev 16, Section 1.6
For the more ambitious matching of the spectrum of the dilatation operator of N=4 D=4 super Yang-Mills theory to the corresponding spectrum of the Green-Schwarz superstring on the super anti de Sitter spacetime detailed checks are summarized in Beisert et al. 10, Escobedo 12
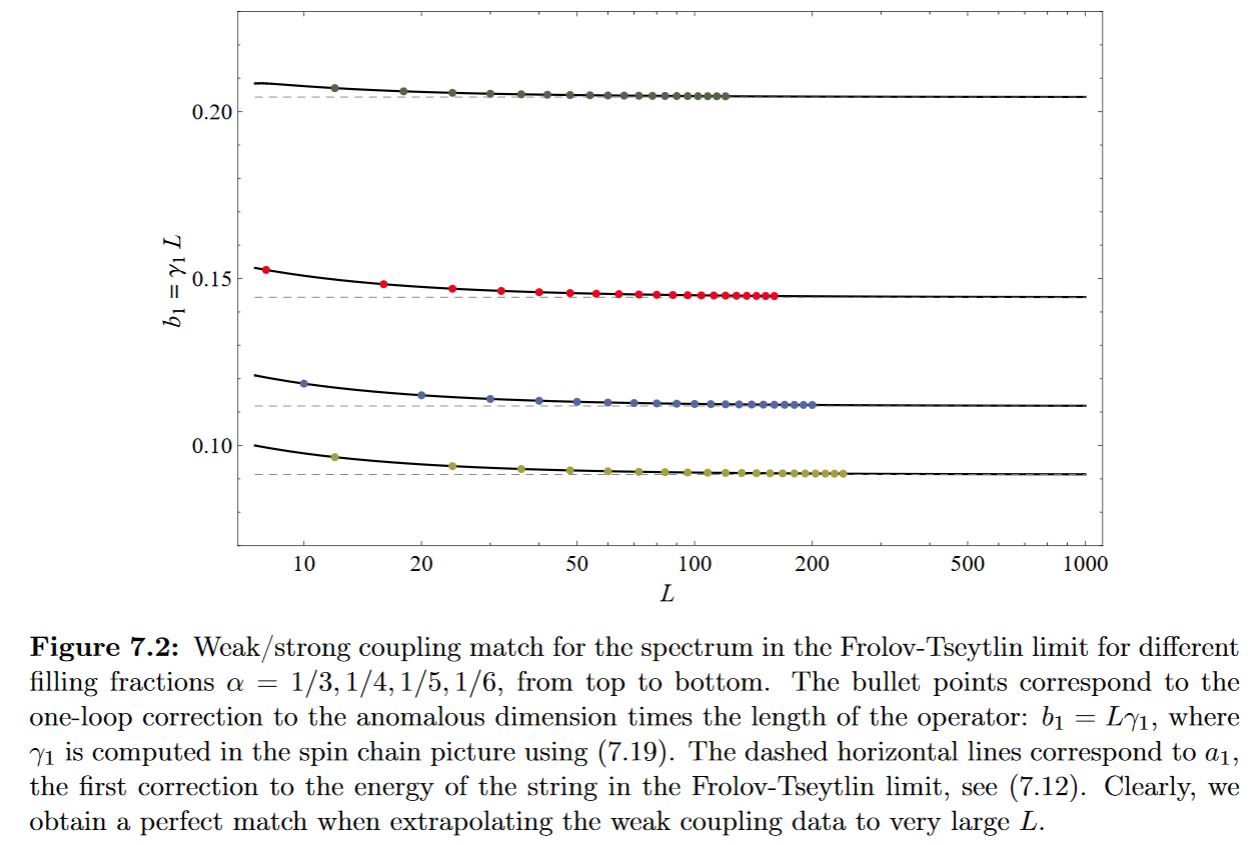
graphics grabbed from Escobedo 12
Comparison to string scattering amplitudes beyond the planar SCFT limit: ABP 18.
Numerical checks using lattice gauge theory are reviewed in Joseph 15.
Exact duality checks pertaining to the full stringy regime for : Eberhardt-Gaberdiel 19a, Eberhardt-Gaberdiel 19b, Eberhardt-Gaberdiel-Gopakumar 19. For more see the references there.
See also
- Umut Gursoy, Guim Planella Planas, Worldsheet from worldline [arXiv:2311.10142]
Examples
The solutions to supergravity that preserve the maximum of 32 supersymmetries are (e.g. HEGKS 08 (1.1))
as well as their Minkowski spacetime and plane wave limits. These are the main KK-compactifications for the following examples-
– Horizon limit of D3-branes
type II string theory on 5d anti de Sitter spacetime (times a 5-sphere) is dual to N=4 D=4 super Yang-Mills theory on the worldvolume of a D3-brane at the asymptotic boundary
(Aharony-Gubser-Maldacena-Ooguri-Oz 99, section 3 and 4)
– Horizon limit of M5-branes
We list some of the conjectured statements and their evidence concerning the case of -duality.
The hypothesis of Maldacena 1997, section 3.1 (for review see (Aharony, Gubser, Maldacena, Ooguri & Oz 1999, section 6.1.1) is that
- the 6d (2,0)-superconformal QFT on the worldvolume of coincident M5-branes
is holographically related to
- 11-dimensional supergravityreduced on the 4-sphere with units of flux of the supergravity C-field to 7d supergravity on an asymptotically anti de Sitter spacetime.
In
- Edward Witten, Five-Brane Effective Action In M-Theory J. Geom. Phys.22:103-133,1997 (arXiv:hep-th/9610234)
effectively this relation was already used to computed the 5-brane partition function in the abelian case from the states of abelian 7d Chern-Simons theory. (The quadratic refinement of the supergravity C-field necessary to make this come out right is what led to Hopkins-Singer 02 and hence to the further mathematical development of differential cohomology and its application in physics.)
In (Witten 98, section 4) this construction is argued for from within the framework of AdS/CFT, explicitly identifying the 7d Chern-Simons theory here with the compactification of the 11-dimensional Chern-Simons term of the supergravity C-field in 11-dimensional supergravity, which locally is
But in fact the quantum anomaly cancellation (GS-type mechanism) for 11d sugra introduces a quantum correction to this Chern-Simons term (DLM, equation (3.14)), making it locally become
where now is the local 1-form representative of a spin connection and where is a Chern-Simons form for the second Pontryagin class and for the first.
That therefore not an abelian, but this nonabelian higher dimensional Chern-Simons theory should be dual to the nonabelian 6d (2,0)-superconformal QFT was maybe first said explicitly in (LuWang 2010).
Its gauge field is hence locally and ignoring the flux quantization subtleties a pair consisting of the abelian 3-form field and a Spin group -valued connection (see supergravity C-field for global descriptions of such pairs). Or maybe rather to account for the constraint that the configurations are to be asymptotic anti de Sitter spacetimes (in analogy to the well-understood situation in 3d quantum gravity, see there for more details).
Indeed, in Sezgin &Sundell 2002, section 7 more detailed arguments are given that the 7-dimensional dual to the free 6d theory is a higher spin gauge theory for a higher spin gauge group extending the (super) conformal group .
A non-perturbative description of this nonabelian 7d Chern-Simons theory as a local prequantum field theory (hence defined non-perturbatively on the global moduli stack of fields (twisted differential string structures, in fact)) was discussed in (FSS 12a, FSS 12b).
General discussion of boundary local prequantum field theories relating higher Chern-Simons-type and higher WZW-type theories is in (dcct 13, section 3.9.14). Specifically, a characterization along these lines of the Green-Schwarz action functional of the M5-brane as a holographic higher WZW-type boundary theory of a 7d Chern-Simons theory is found in (FSS 13).
Analogous discussion of the 6d theory as a higher WZW analog of a 7d Chern-Simons theory phrased in terms of extended quantum field theory is (Freed 12).
–Horizon limit of M2-branes
11d supergravity/M-theory on the asymptotic
spacetime of an M2-brane.
(Maldacena 97, section 3.2, Aharony-Gubser-Maldacena-Ooguri-Oz 99, section 6.1.2, Klebanov-Torri 10)
– Horizon limit of D-D() brane bound states
(for more see at AdS3-CFT2 and CS-WZW correspondence)
D1-D5 brane system in type IIB string theory
(Aharony-Gubser-Maldacena-Ooguri-Oz 99, section 5)
D6-D8 brane bound state with D2-D4 brane bound state defects in massive type IIA string theory
(Dibitetto-Petri 17, …)
D4-D8 brane bound state with D2-D6 brane bound state defects in massive type IIA string theory
(Dibitetto-Petri 18, …)
see at nearly AdS2/CFT1
Non-conformal duals
Horizon limit of -branes for arbitrary
(Aharony-Gubser-Maldacena-Ooguri-Oz 99, section 6.1.3)
Horizon limit of NS5-brane
(Aharony-Gubser-Maldacena-Ooguri-Oz 99, section 6.1.4)
QCD models
While all of the above horizon limits product super Yang-Mills theory, one can consider certain limits of these in which they look like plain QCD, at least in certain sectors. This leads to a discussion of holographic description of QCD properties that are actually experimentally observed.
(Aharony-Gubser-Maldacena-Ooguri-Oz 99, section 6.2)
See the References – Applications – In condensed matter physics.
Further gauge theories induced by compactification and twisting
gauge theory induced via AdS-CFT correspondence
| M-theory perspective via AdS7-CFT6 | F-theory perspective |
|---|---|
| 11d supergravity/M-theory | |
| Kaluza-Klein compactification on | compactificationon elliptic fibration followed by T-duality |
| 7-dimensional supergravity | |
| topological sector | |
| 7-dimensional Chern-Simons theory | |
| AdS7-CFT6 holographic duality | |
| 6d (2,0)-superconformal QFT on the M5-brane with conformal invariance | M5-brane worldvolume theory |
| KK-compactification on Riemann surface | double dimensional reduction on M-theory/F-theory elliptic fibration |
| N=2 D=4 super Yang-Mills theory with Montonen-Olive S-duality invariance; AGT correspondence | D3-brane worldvolume theory with type IIB S-duality |
| topological twist | |
| topologically twisted N=2 D=4 super Yang-Mills theory | |
| KK-compactification on Riemann surface | |
| A-model on , Donaldson theory |
Formalizations
The full formalization of AdS/CFT is still very much out of reach, but maybe mostly for lack of trying.
But see Anderson 04.
One proposal for a formalization of a toy version in the context of AQFT is Rehren duality. However, it does not seem that this actually formalizes AdS-CFT, but something else.
Related concepts
-
dS/CFT correspondence?
Table of branes appearing in supergravity/string theory (for classification see at brane scan).
References
Long before the modern formulation of the AdS/CFT correspondence, referenced below at
there were developments that must be regarded at least as precursors, referenced at
Polyakov gauge/string duality
Key ideas underlying what is now known as holographic duality in string theory and specifically as holographic QCD (see notably also at holographic light front QCD) were preconceived by Alexander Polyakov (cf. historical remarks in Polyakov (2008)) under the name gauge/string duality (cf. historical review in Polyakov (2008)), in efforts to understand confined QCD (the mass gap problem) by regarding color-flux tubes (Wilson lines) between quarks as dynamical strings:
Early suggestion that confined QCD is described by regarding the color-flux tubes as string-like dynamical degrees of freedoms:
-
John Kogut, Leonard Susskind, Vacuum polarization and the absence of free quarks in four dimensions, Phys. Rev. D 9 (1974) 3501-3512 [doi:10.1103/PhysRevD.9.3501]
-
Kenneth G. Wilson, Confinement of quarks, Phys. Rev. D 10 (1974) 2445 [doi:10.1103/PhysRevD.10.2445]
(argument in lattice gauge theory)
-
John Kogut, Leonard Susskind, Hamiltonian formulation of Wilson’s lattice gauge theories, Phys. Rev. D 11 (1975) 395 [doi:10.1103/PhysRevD.11.395]
“The gauge-invariant configuration space consists of a collection of strings with quarks at their ends. The strings are lines of non-Abelian electric flux. In the strong coupling limit the dynamics is best described in terms of these strings. Quark confinement is a result of the inability to break a string without producing a pair. […]”
“The confining mechanism is the appearance of one dimensional electric flux tubes which must link separated quarks. The appropriate description of the strongly coupled limit consists of a theory of interacting, propagating strings. […]”
“This picture of the strongly coupled Yang-Mills theory in terms of a collection of stringlike flux lines is the central result of our analysis. It should be compared with the phenomenological use of stringlike degrees of freedom which has been widely used in describing hadrons.”
-
Alexander Polyakov, String representations and hidden symmetries for gauge fields, Physics Letters B 82 2 (1979) 247-250 [doi:10.1016/0370-2693(79)90747-0]
-
Alexander Polyakov, Gauge fields as rings of glue, Nuclear Physics B 164 (1980) 171-188 [doi:10.1016/0550-3213(80)90507-6]
“The basic idea is that gauge fields can be considered as chiral fields, defined on the space of all possible contours (the loop space). The origin of the idea lies in the expectation that, in the confining phase of a gauge theory, closed strings should play the role of elementary excitations.”
-
Yuri Makeenko, Alexander A. Migdal, Quantum chromodynamics as dynamics of loops, Nuclear Physics B 188 2 (1981) 269-316 [doi:10.1016/0550-3213(81)90258-3]
“So the world sheet of string should be interpreted as the color magnetic dipole sheet. The string itself should be interpreted as the electric flux tube in the monopole plasma.”
-
Alexander Polyakov, Gauge Fields and Strings, Routledge, Taylor and Francis (1987, 2021) [doi:10.1201/9780203755082, oapen:20.500.12657/50871]
old personal page]: “My main interests this year [1993?] were directed towards string theory of quark confinement. The problem is to find the string Lagrangian for the Faraday’s ”lines of force“,which would reproduce perturbative corrections from the Yang-Mills theory to the Coulomb law at small distances and would give permanent confinement of quarks at large distances.”
Cf. also
-
M. Lüscher: Symmetry-breaking aspects of the roughening transition in gauge theories, Nuclear Physics B 180 2 (1981) 317-329 [doi:10.1016/0550-3213(81)90423-5]
-
Alexei Morozov, p. 6 of: String theory: what is it?, Sov. Phys. Usp. 35 (1992) 671-714 [doi:10.1070/PU1992v035n08ABEH002255]
Early suggestion, due to the Liouville field seen in the quantization of the bosonic string via the Polyakov action,
- Alexander Polyakov, Quantum geometry of bosonic strings, Phys. Lett. B 103 (1981) 207-210 [doi:10.1016/0370-2693(81)90743-7, pdf]
that such flux tubes regarded as confining strings are to be thought of a probing higher dimensional spacetime, exhibiting a holographic principle in which actual spacetime appears as a brane:
-
Alexander Polyakov, String Theory and Quark Confinement, talk at Strings’97, Nucl. Phys. Proc. Suppl. 68 (1998) 1-8 [doi:10.1016/S0920-5632(98)00135-2, arXiv:hep-th/9711002]
“In other words the open string flies in the -space keeping its feet (its ends) on the ground .”
-
Alexander Polyakov, The wall of the cave, Int. J. Mod. Phys. A 14 (1999) 645-658 arXiv:hep-th/9809057, doi:10.1142/S0217751X99000324
“We add new arguments that the Yang-Mills theories must be described by the non-critical strings in the five dimensional curved space. The physical meaning of the fifth dimension is that of the renormalization scale represented by the Liouville field.”
eventually culminating in the formulation of the dictionary for the AdS-CFT correspondence:
- Steven Gubser, Igor Klebanov, Alexander Polyakov, Gauge theory correlators from non-critical string theory, Physics Letters B 428 105-114 (1998) [doi:10.1016/S0370-2693(98)00377-3, hep-th/9802109]
“Relations between gauge fields and strings present an old, fascinating and unanswered question. The full answer to this question is of great importance for theoretical physics. It will provide us with a theory of quark confinement by explaining the dynamics of color-electric fluxes.”
- Alexander Polyakov, Vyacheslav Rychkov Gauge fields-strings duality and the loop equation, Nucl. Phys. B 581 (2000) 116-134 [doi:10.1016/S0550-3213(00)00183-8, arXiv:hep-th/0002106]
and the suggestion of finding the string-QCD correspondence:
- Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A 17 S1 (2002) 119-136 [doi:10.1142/S0217751X02013071, arXiv:hep-th/0110196]
“in the strong coupling limit of a lattice gauge theory the elementary excitations are represented by closed strings formed by the color-electric fluxes. In the presence of quarks these strings open up and end on the quarks, thus guaranteeing quark confinement. Moreover, in the gauge theory the strings interaction is weak at large . This fact makes it reasonable to expect that also in the physically interesting continuous limit (not accessible by the strong coupling approximation) the best description of the theory should involve the flux lines (strings) and not fields, thus returning us from Maxwell to Faraday. In other words it is natural to expect an exact duality between gauge fields and strings. The challenge is to build a precise theory on the string side of this duality.”
Historical reminiscences:
- Alexander Polyakov, Confinement and Liberation, in Gerardus ’t Hooft (ed.) 50 Years of Yang-Mills Theory (2005) 311-329 [arXiv:hep-th/0407209, doi:10.1142/9789812567147_0013, doi:10.1142/5601]
“Already in 1974, in his famous large paper, ‘t Hooft already tried to find the string-gauge connections. His idea was that the lines of Feynman’s diagrams become dense in a certain sense and could be described as a 2d surface. This is, however, very different from the picture of strings as flux lines. Interestingly, even now people often don’t distinguish between these approaches. In fact, for the usual amplitudes Feynman’s diagrams don’t become dense and the flux lines picture is an appropriate one. However there are cases in which t’Hooft’s mechanism is really working.”
-
Alexander M. Polyakov, §1 in: Beyond Space-Time, in The Quantum Structure of Space and Time, Proceedings of the 23rd Solvay Conference on Physics, World Scientific (2007) [arXiv:hep-th/0602011, pdf]
-
Alexander M. Polyakov, From Quarks to Strings [arXiv:0812.0183]
published as Quarks, strings and beyond, section 44 in: Paolo Di Vecchia et al. (ed.), The Birth of String Theory, Cambridge University Press (2012) 544-551 [doi:10.1017/CBO9780511977725.048]
“By the end of ’77 it was clear to me that I needed a new strategy for understanding confinement and I became convinced that the way to go was the gauge/string duality. […]” “Classically the string is infinitely thin and has only transverse oscillations. But when I quantized it there was a surprise – an extra, longitudinal mode, which appears due to the quantum ”thickening“ of the string. This new field is called the Liouville mode. […]”
“I kept thinking about gauge/strings dualities. Soon after the Liouville mode was discovered it became clear to many people including myself that its natural interpretation is that random surfaces in 4d are described by the strings flying in 5d with the Liouville field playing the role of the fifth dimension. The precise meaning of this statement is that the wave function of the general string state depends on the four center of mass coordinates and also on the fifth, the Liouville one. In the case of minimal models this extra dimension is related to the matrix eigenvalues and the resulting space is flat.”
“Since this 5d space must contain the flat 4d subspace in which the gauge theory resides, the natural ansatz for the metric is just the Friedman universe with a certain warp factor. This factor must be determined from the conditions of conformal symmetry on the world sheet. Its dependence on the Liouville mode must be related to the renormalization group flow. As a result we arrive at a fascinating picture – our 4d world is a projection of a more fundamental 5d string theory. […]”
“At this point I was certain that I have found the right language for the gauge/string duality. I attended various conferences, telling people that it is possible to describe gauge theories by solving Einstein-like equations (coming from the conformal symmetry on the world sheet) in five dimensions. The impact of my talks was close to zero. That was not unusual and didn’t bother me much. What really caused me to delay the publication (Polyakov 1998) for a couple of years was my inability to derive the asymptotic freedom from my equations. At this point I should have noticed the paper of Klebanov 1997 in which he related D3 branes described by the supersymmetric Yang Mills theory to the same object described by supergravity. Unfortunately I wrongly thought that the paper is related to matrix theory and I was skeptical about this subject. As a result I have missed this paper which would provide me with a nice special case of my program. This special case was presented little later in full generality by Juan Maldacena (Maldacena 1997) and his work opened the flood gates.”
A detailed monograph:
-
N. D. Hari Dass, Strings to Strings – Yang-Mills Flux Tubes, QCD Strings and Effective String Theories, Lecture Notes in Physics 1018, Springer (2024) [doi:10.1007/978-3-031-35358-1]
Ch. 23:
Effective String Theories (EST) of Yang-Mills Flux Tubes [doi:10.1007/978-3-031-35358-1_22, arXiv:2312.10629]
Discussion of corrections of flux tube-dynamics beyond the Nambu-Goto action:
-
Michele Caselle, Nicodemo Magnoli, Alessandro Nada, Marco Panero, Dario Panfalone, Lorenzo Verzichelli: Confining strings in three-dimensional gauge theories beyond the Nambu–Gotō approximation, J. High Energ. Phys. 2024 198 (2024) [doi:10.1007/JHEP08(2024)198, arXiv:2407.10678]
-
Michele Caselle, Nicodemo Magnoli, Alessandro Nada, Marco Panero, Dario Panfalone, Lorenzo Verzichelli: Effective String Theory of three-dimensional gauge theories beyond the Nambu–Gotō approximation [arXiv:2412.14204]
Microscopic AdS/CFT via -brane sigma-models
Over a decade before the modern formulation of the AdS-CFT correspondence, a candicate “microscopic” explanation was observed:

Immersing the worldvolume of a sigma-model super -brane (hence a “light” brane without backreaction) along the near horizon geometry (an AdS supergravity solution) of its own black brane incarnation (hence the “heavy” incarnation of the same brane, causing backreaction), its worldvolume fluctuations (after super-diffeomorphism gauge fixing) are described by the corresponding superconformal field theory (exhibited by superconformal multiplets such as “supersingletons”) [graphics from GSS24].
The original observation for the M2-brane:
-
Eric Bergshoeff, Michael Duff, Christopher Pope, Ergin Sezgin: Supersymmetric Supermembrane Vacua and Singletons, Phys. Lett. B 199 (1987) 69-74 [doi:10.1016/0370-2693(87)91465-1, InSpire:250244]
-
Miles P. Blencowe, Mike Duff, Supersingletons, Physics letters B, 203 3 (1988) 229-236 [doi:10.1016/0370-2693(88)90544-8, cds:184143]
-
Gianguido Dall'Agata, Davide Fabbri, Christophe Fraser, Pietro Fré, Piet Termonia, Mario Trigiante, The singleton action from the supermembrane, Nucl. Phys. B 542 (1999) 157-194 [doi:10.1016/S0550-3213(98)00765-2, arXiv:hep-th/9807115]
with popular exposition in:
- Mike Duff, Christine Sutton: The Membrane at the End of the Universe, New Scientist 118 (1988) 67-71 [inspire:268230, ISSN:0028-6664]
Further discussion including also M5-branes and D-branes:
-
Piet Claus, Renata Kallosh, Antoine Van Proeyen, M 5-brane and superconformal tensor multiplet in 6 dimensions, Nucl. Phys. B 518 (1998) 117-150 [doi:10.1016/S0550-3213(98)00137-0, arXiv:hep-th/9711161]
-
Piet Claus, Renata Kallosh, J. Kumar, Paul K. Townsend, Antoine Van Proeyen, Conformal Theory of M2, D3, M5 and “D1+D5” Branes, JHEP 9806 (1998) 004 [doi:10.1088/1126-6708/1998/06/004, arXiv:hep-th/9801206]
-
Paolo Pasti, Dmitri Sorokin, Mario Tonin, Branes in Super-AdS Backgrounds and Superconformal Theories, Proceedings, International Workshop on Supersymmetries and Quantum Symmetries (SQS’99), Moscow (July 27-31, 1999) [arXiv:hep-th/9912076, inspire:511348]
-
C. Grojean, J. Mourad, Super fivebranes near the boundary of , Nuclear Physics B 567 1–2 (2000) 133-150 [doi:10.1016/S0550-3213(99)00335-1, arXiv:hep-th/9903164]
-
Alexei Nurmagambetov, I. Y. Park On the M5 and the correspondence, Physics Letters B
524 1–2 (2002) 185-191 [doi:10.1016/S0370-2693(01)01375-2, arXiv:hep-th/0110192]
Review:
-
Mike Duff, Anti-de Sitter space, branes, singletons, superconformal field theories and all that, Int. J. Mod. Phys. A 14 (1999) 815-844 [doi:10.1142/S0217751X99000403, arXiv:hep-th/9808100]
-
Mike Duff, TASI Lectures on Branes, Black Holes and Anti-de Sitter Space, lectures at 9th CRM Summer School: Theoretical Physics at the End of the 20th Century at TASI 99 (1999) [arXiv:hep-th/9912164, inspire:511822]
The resulting super-conformal brane scan:
-
Michael Duff, Near-horizon brane-scan revived, Nucl. Phys. B 810 (2009) 193-209 [doi:10.1016/j.nuclphysb.2008.11.001, arXiv:0804.3675]
-
Michael Duff, The conformal brane-scan: an update, J. High Energ. Phys. 2022 54 (2022) [doi:10.1007/JHEP06(2022)054, arXiv:2112.13784]
Related:
- Hironori Mori, Satoshi Yamaguchi, §3 in: M5-branes and Wilson Surfaces in AdS7/CFT6 Correspondence, Phys. Rev. D 90 (2014) 026005 [doi:10.1103/PhysRevD.90.026005, arXiv:1404.0930]
Analogous discussion for embeddings with less supersymmetry, corresponding to defects
-
Nadav Drukker, Simone Giombi, Arkady A. Tseytlin, Xinan Zhou, Defect CFT in the 6d theory from M2 brane dynamics in , J. High Energ. Phys. 2020 101 (2020) [doi:10.1007/JHEP07(2020)101, arXiv:2004.04562]
-
Varun Gupta, Holographic M5 branes in , J. High Energ. Phys. 2021 32 (2021) [doi:10.1007/JHEP12(2021)032, arXiv:2109.08551]
-
Varun Gupta, More Holographic M5 branes in , Phys. Lett. B 853 (2024) 138650 [doi:10.1016/j.physletb.2024.138650, arXiv:2301.02528]
The origin of modern AdS/CFT duality
The modern guise of AdS/CFT duality as a conjectured duality between string/M-theory near black branes and superconformal field theories on the worldvolume of these branes, at least in a suitable large-N limit, is due to:
-
Juan Maldacena, The Large limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys. 2 (1998) 231 [hep-th/9711200, doi:10.4310/ATMP.1998.v2.n2.a1, inspire:451647]
-
Juan Maldacena, Wilson loops in Large field theories, Phys. Rev. Lett. 80 (1998) 4859 [hep-th/9803002, doi:10.1103/PhysRevLett.80.4859]
An actual rule for matching, under this duality, bulk states to generating functions for boundary correlators/n-point functions was then given by
-
Steven Gubser, Igor Klebanov, Alexander Polyakov, around (12) of: Gauge theory correlators from non-critical string theory, Physics Letters B 428 105-114 (1998) [hep-th/9802109, doi:10.1016/S0370-2693(98)00377-3]
-
Edward Witten, around (2.11) of Anti-de Sitter space and holography, Advances in Theoretical and Mathematical Physics 2 (1998) 253-291 [hep-th/9802150, doi:10.4310/ATMP.1998.v2.n2.a2, spire:467400]
now often called “the holographic disctionary” or just “the dictionary” (e.g. Taylor 2023).
See also:
-
Wikipedia, AdS/CFT correspondence
-
Tom Banks, Michael Douglas, Gary Horowitz, Emil Martinec, AdS Dynamics from Conformal Field Theory (arXiv:hep-th/9808016, spire:474214)
-
Carlos Andrés Cardona Giraldo, Correlation functions in AdS/CFT correspondence, 2012 (spire:1652794, pdf)
Sketch of a derivation of AdS/CFT:
-
Horatiu Nastase, Towards deriving the AdS/CFT correspondence (arXiv:1812.10347)
-
Ofer Aharony, Shai Chester, Erez Urbach, A Derivation of AdS/CFT for Vector Models (arXiv:2011.06328)
See also:
-
Edward Witten, Three-dimensional gravity revisited, arxiv/0706.3359
-
C. R. Graham, Edward Witten, Conformal anomaly of submanifold observables in AdS/CFT correspondence, hepth/9901021.
-
Edward Witten, AdS/CFT Correspondence And Topological Field Theory (arXiv:hep-th/9812012)
- Oscar Varela: Super-Chern-Simons spectra from Exceptional Field Theory, J. High Energ. Phys. 2021 283 (2021) [arXiv:2010.09743, doi:10.1007/JHEP04(2021)283]
Introductions and surveys
-
Edward Witten, Baryons and Branes in Anti de Sitter Space talk at String98 (1998) [web]
(by the title, apparently originally intended to touch on AdS-QCD, but de facto ending with focus on the problem of flat space holography)
-
Alexander Polyakov, The wall of the cave, Int. J. Mod. Phys. A 14 (1999) 645-658 [arXiv:hep-th/9809057, doi:10.1142/S0217751X99000324]
(early account with focus on AdS-QCD duality)
-
John Schwarz, Introduction to M Theory and AdS/CFT Duality, in: Quantum Aspects of Gauge Theories, Supersymmetry and Unification Lecture Notes in Physics 525, Springer (1999) [arXiv:hep-th/9812037, doi:10.1007/BFb0104239]
(early review with an eye towards M-theory)
-
Jens L. Petersen, Introduction to the Maldacena Conjecture on AdS/CFT, Int. J. Mod. Phys. A 14 (1999) 3597-3672 [hep-th/9902131, doi:10.1142/S0217751X99001676]
-
Ofer Aharony, Steven Gubser, Juan Maldacena, Hirosi Ooguri, Yaron Oz, Large Field Theories, String Theory and Gravity, Phys. Rept. 323 183-386 (2000) [doi:10.1016/S0370-1573(99)00083-6, arXiv:hep-th/9905111]
-
Jan de Boer, Introduction to AdS/CFT correspondence, talk at SUSY02 (2002) [pdf, pdf]
-
Michael T. Anderson, Geometric aspects of the AdS/CFT correspondence [arXiv:hep-th/0403087]
-
Christopher P. Herzog, Igor R. Klebanov: AdS/CFT Correspondence, Encyclopedia of Mathematical Physics, Academic Press (2006) 174-183 [doi:10.1016/B0-12-512666-2/00245-5, pdf]
-
Horatiu Nastase, Introduction to AdS-CFT [arXiv:0712.0689]
-
Horatiu Nastase, Introduction to AdS/CFT correspondence, Cambridge University Press (2015) [cds:1984145, doi:10.1017/CBO9781316090954]
-
Gary Horowitz, Joseph Polchinski, Gauge/gravity duality [gr-qc/0602037]
-
Alberto Zaffaroni, Introduction to the AdS/CFT correspondence, LACES lectures (2009) [pdf, pdf]
-
Hans Günter Dosch, A Practical Guide to AdS/CFT, lecture notes (2009) [pdf, pdf]
(with aspects of holographic QCD)
-
Joseph Polchinski, Introduction to Gauge/Gravity Duality (arXiv:1010.6134)
-
Christopher Herzog, AdS/CFT, lecture notes (2015) [pdf, pdf]
-
Makoto Natsuume, AdS/CFT Duality User Guide, Lecture Notes in Physics 903, Springer (2015) [arXiv:1409.3575, doi:10.1007/978-4-431-55441-7, webpage]
-
Sebastian De Haro, Daniel R. Mayerson, Jeremy Butterfield, Conceptual Aspects of Gauge/Gravity Duality, Foundations of Physics 46 11 (2016) 1381-1425 [arXiv:1509.09231, doi:10.1007/s10701-016-0037-4]
-
Johanna Erdmenger, Introduction to Gauge/Gravity Duality, PoS TASI2017 (2018) 001 [arXiv:1807.09872, doi:10.22323/1.305.0001]
(focus on holographic entanglement entropy and AdS/CMT duality)
-
Matteo Baggioli: Applied Holography – A Practical Mini-Course, Springer Briefs in Physics, Springer (2019) [doi:10.1007/978-3-030-35184-7]
-
Nirmalya Kajuri, ST4 Lectures on Bulk Reconstruction [arXiv:2003.00587]
-
Francesco Benini: Brief Introduction to AdS/CFT SISSA lecture (2022) [pdf, pdf]
-
Marika Taylor, Introduction to AdS/CFT and Holography – The holographic dictionary, lecture at pre-SUSY school 2023 [cern:1214657, slides: pdf, video: session 1, sessions 2, 3]
Review of Yangian symmetry:
- Alessandro Torrielli, Yangians, S-matrices and AdS/CFT, J. Phys. A 44 263001 (2011) [arXiv:1104.2474]
Lattice gauge theory computations
Review of lattice gauge theory-numerics for the AdS-CFT correspondence:
- Anosh Joseph, Review of Lattice Supersymmetry and Gauge-Gravity Duality (arXiv:1509.01440)
Using the KK-compactification of D=4 N=4 super Yang-Mills theory to the BMN matrix model for lattice gauge theory-computations in D=4 N=4 SYM and for numerical checks of the AdS-CFT correspondence:
- Masazumi Honda, Goro Ishiki, Sang-Woo Kim, Jun Nishimura, Asato Tsuchiya, Direct test of the AdS/CFT correspondence by Monte Carlo studies of N=4 super Yang-Mills theory, JHEP 1311 (2013) 200 (arXiv:1308.3525)
On single trace operators
The correspondence of single trace operators to superstring excitations under the AdS-CFT correspondence originates with these articles:
-
Alexander Polyakov, Gauge Fields and Space-Time, Int. J. Mod. Phys. A17S1 (2002) 119-136 [arXiv:hep-th/0110196, doi:10.1142/S0217751X02013071]
-
David Berenstein, Juan Maldacena, Horatiu Nastase, Strings in flat space and pp waves from Super Yang Mills, JHEP 0204 (2002) 013 (arXiv:hep-th/0202021)
(whence “BMN operators”)
-
Steven Gubser, Igor Klebanov, Alexander Polyakov, A semi-classical limit of the gauge/string correspondence, Nucl. Phys. B 636 (2002) 99-114 [arXiv:hep-th/0204051, doi:10.1016/S0550-3213(02)00373-5]
-
Martin Kruczenski, Spiky strings and single trace operators in gauge theories, JHEP 0508:014, 2005 (arXiv:hep-th/0410226)
The identification of the relevant single trace operators with integrable spin chains is due to
-
J. A. Minahan, Konstantin Zarembo, The Bethe-Ansatz for Super Yang-Mills, JHEP 0303 (2003) 013 (arXiv:hep-th/0212208)
-
Niklas Beisert, Matthias Staudacher, The SYM Integrable Super Spin Chain,
Nucl. Phys. B670:439-463, 2003 (arXiv:hep-th/0307042)
which led to more detailed matching of single trace operators to rotating string excitations in
- Niklas Beisert, Sergey Frolov, Matthias Staudacher, Arkady Tseytlin, Precision Spectroscopy of AdS/CFT, JHEP 0310:037, 2003 (arXiv:hep-th/0308117)
Review includes
-
A. V. Belitsky, Volker Braun, A. S. Gorsky, G. P. Korchemsky, Integrability in QCD and beyond, Int. J. Mod. Phys. A19:4715-4788, 2004 (arXiv:hep-th/0407232)
-
Niklas Beisert, Luis Alday, Radu Roiban, Sakura Schafer-Nameki, Matthias Staudacher, Alessandro Torrielli, Arkady Tseytlin, et. al., Review of AdS/CFT Integrability: An Overview, Lett. Math. Phys. 99, 3 (2012) (arXiv:1012.3982)
SYK-model in
Discussion of the SYK-model as the AdS/CFT dual of JT-gravity in nearly AdS2/CFT1 and AdS-CFT in condensed matter physics:
Original articles:
-
Juan Maldacena, Douglas Stanford, Comments on the Sachdev-Ye-Kitaev model, Phys. Rev. D 94, 106002 (2016)(arXiv:1604.07818)
-
Subir Sachdev, Holographic metals and the fractionalized Fermi liquid, Phys. Rev. Lett. 105:151602, 2010 (arXiv:1006.3794)
Review:
-
Gábor Sárosi, holography and the SYK model, Proceedings of Science 323 (arXiv:1711.08482, doi:10.22323/1.323.0001)
-
Juan Maldacena, Toy models for black holes II, talk at PiTP 2018 From QBits to spacetime (recording)
-
Dmitrii A. Trunin, Pedagogical introduction to SYK model and 2D Dilaton Gravity (arXiv:2002.12187)
Relation to black holes in terms of Majorana dimer states:
- Ioanna Kourkoulou, Juan Maldacena, Pure states in the SYK model and nearly- gravity (arXiv:1707.02325)
Relation to black holes in string theory and random matrix theory:
-
Jordan S. Cotler, Guy Gur-Ari, Masanori Hanada, Joseph Polchinski, Phil Saad, Stephen Shenker, Douglas Stanford, Alexandre Streicher, Masaki Tezuka, Black Holes and Random Matrices, JHEP 1705:118, 2017 (arXiv:1611.04650)
-
Tomoki Nosaka, Tokiro Numasawa, Quantum Chaos, Thermodynamics and Black Hole Microstates in the mass deformed SYK model (arXiv:1912.12302)
On non-perturbative effects and resurgence:
- Paolo Gregori, Ricardo Schiappa, From Minimal Strings towards Jackiw-Teitelboim Gravity: On their Resurgence, Resonance, and Black Holes (arXiv:2108.11409)
See also
-
Yuri D. Lensky, Xiao-Liang Qi, Pengfei Zhang, Size of bulk fermions in the SYK model (arXiv:2002.01961)
-
Xiao-Liang Qi, Pengfei Zhang, The Coupled SYK model at Finite Temperature (arXiv:2003.03916)
-
Akash Goel, Herman Verlinde, Towards a String Dual of SYK (arXiv:2103.03187)
-
Tarek Anous, Felix M. Haehl, The quantum -spin glass model: A user manual for holographers (arXiv:2106.03838)
Discussion of small N corrections via a lattice QFT-Ansatz on the AdS side:
- Richard C. Brower, Cameron V. Cogburn, A. Liam Fitzpatrick, Dean Howarth, Chung-I Tan, Lattice Setup for Quantum Field Theory in (arXiv:1912.07606)
See also:
- Gregory J. Galloway, Melanie Graf, Eric Ling, A conformal infinity approach to asymptotically spacetimes (arXiv:2003.00093)
Random matrix theory in
On Jackiw-Teitelboim gravity dual to random matrix theory (via AdS2/CFT1 and topological recursion):
-
Ahmed Almheiri, Joseph Polchinski, Models of Backreaction and Holography, J. High Energ. Phys. 2015 14 (2015) [arXiv:1402.6334]
-
Phil Saad, Stephen Shenker, Douglas Stanford, JT gravity as a matrix integral (arXiv:1903.11115)
-
Douglas Stanford, Edward Witten, JT Gravity and the Ensembles of Random Matrix Theory (arXiv:1907.03363)
-
Ping Gao, Daniel L. Jafferis, David K. Kolchmeyer, An effective matrix model for dynamical end of the world branes in Jackiw-Teitelboim gravity, J. High Energ. Phys. 2022 38 (2022) [doi:10.1007/JHEP01(2022)038, arXiv:2104.01184]
BFSS matrix model in
On AdS2/CFT1 with the BFSS matrix model on the CFT side and black hole-like solutions in type IIA supergravity on the AdS side:
- Juan Maldacena, Alexey Milekhin, To gauge or not to gauge?, JHEP 04 (2018) 084 (arxiv:1802.00428)
and on its analog of holographic entanglement entropy:
- Tarek Anous, Joanna L. Karczmarek, Eric Mintun, Mark Van Raamsdonk, Benson Way, Areas and entropies in BFSS/gravity duality (arXiv:1911.11145)
See also
- Takeshi Morita, Hiroki Yoshida, A Critical Dimension in One-dimensional Large-N Reduced Models (arXiv:2001.02109)
Flat space limit
The SYK model in flat space holography:
- Hamid Afshar, Hernan Gonzalez, Daniel Grumiller, Dmitri Vassilevich, Flat space holography and complex SYK, Phys. Rev. D 101, 086024 (arXiv:1911.05739, doi:10.1103/PhysRevD.101.086024)
D1-D3 brane intersections in
On D1-D3 brane intersections in AdS2/CFT1:
- Giuseppe Dibitetto, Yolanda Lozano, Nicolò Petri, Anayeli Ramirez, Holographic Description of M-branes via (arXiv:1912.09932)
Via T-duality from D6-D8 brane intersections:
- Yolanda Lozano, Carlos Nunez, Anayeli Ramirez, Stefano Speziali, New backgrounds and Conformal Quantum Mechanics (arXiv:2011.00005)
Chord diagrams and weight systems in Physics
The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:
-
In quantum many body models for for holographic brane/bulk correspondence:
For a unifying perspective (via Hypothesis H) and further pointers, see:
-
Hisham Sati, Urs Schreiber, Differential Cohomotopy implies intersecting brane observables, Adv. Theor. Math. Phys. 26 4 (2022) [doi:10.4310/ATMP.2022.v26.n4.a4arXiv:1912.10425]
-
David Corfield, Hisham Sati, Urs Schreiber: Fundamental weight systems are quantum states Lett. Math. Phys. 113 112 (2023) [arXiv:2105.02871, doi:10.1007/s11005-023-01725-4]
-
Carlo Collari, A note on weight systems which are quantum states, Can. Math. Bull. 66 4 (2023) [doi:10.4153/S0008439523000206, arXiv:2210.05399]
Review:
- Carlo Collari, Weight systems which are quantum states, talk at QFT and Cobordism, CQTS (Mar 2023) web, pdf
In Chern-Simons theory
Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.
Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.
-
Dror Bar-Natan, Perturbative aspects of the Chern-Simons topological quantum field theory, thesis 1991 (spire:323500, proquest:303979053, BarNatanPerturbativeCS91.pdf)
-
Maxim Kontsevich, Vassiliev’s knot invariants, Advances in Soviet Mathematics, Volume 16, Part 2, 1993 (pdf)
-
Daniel Altschuler, Laurent Freidel, Vassiliev knot invariants and Chern-Simons perturbation theory to all orders, Commun. Math. Phys. 187 (1997) 261-287 (arxiv:q-alg/9603010)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Configuration spaces and Vassiliev classes in any dimension, Algebr. Geom. Topol. 2 (2002) 949-1000 (arXiv:math/9910139)
-
Alberto Cattaneo, Paolo Cotta-Ramusino, Riccardo Longoni, Algebraic structures on graph cohomology, Journal of Knot Theory and Its Ramifications, Vol. 14, No. 5 (2005) 627-640 (arXiv:math/0307218)
Reviewed in:
- Ismar Volić, Section 4 of: Configuration space integrals and the topology of knot and link spaces, Morfismos, Vol 17, no 2, 2013 (arxiv:1310.7224)
Applied to Gopakumar-Vafa duality:
- Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)
See also
-
Marcos Mariño, Chern-Simons theory, matrix integrals, and perturbative three-manifold invariants, Commun. Math. Phys. 253 (2004) 25-49 (arXiv:hep-th/0207096)
-
Stavros Garoufalidis, Marcos Mariño, On Chern-Simons matrix models (pdf, pdf)
For single trace operators in AdS/CFT duality
Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics
- Micha Berkooz, Prithvi Narayan, Joan Simón, Section 2.1 of Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
In , JT-gravity/SYK-model
Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:
-
Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order , JHEP 04 (2018) 146 (arXiv:1801.02696)
-
Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)
-
Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)
following:
- László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)
which in turn follows
- Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)

With emphasis on the holographic content:
-
Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)
-
Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large Double-Scaled SYK, 2019 (pdf)
-
Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative , and chords in the double-scaled SYK model [arXiv:2212.13668]
-
Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]
-
Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]
and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)
-
Andreas Blommaert, Thomas Mertens, Henri Verschelde, Fine Structure of Jackiw-Teitelboim Quantum Gravity, JHEP 1909 (2019) 066 (arXiv:1812.00918)
-
Henry W. Lin, The bulk Hilbert space of double scaled SYK, J. High Energ. Phys. 2022 60 (2022) arXiv:2208.07032, doi:10.1007/JHEP11(2022)060
-
Henry W. Lin, Douglas Stanford, A symmetry algebra in double-scaled SYK arXiv:2307.15725
-
Micha Berkooz, Ohad Mamroud: A Cordial Introduction to Double Scaled SYK [arXiv:2407.09396]
-
Adel A. Rahman, Leonard Susskind: -Chords, Wee-Chords, and de Sitter Space [arXiv:2407.12988]
In D/D-brane intersections
Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):
-
Sanyaje Ramgoolam, Bill Spence, S. Thomas, Section 3.2 of: Resolving brane collapse with corrections in non-Abelian DBI, Nucl. Phys. B703 (2004) 236-276 (arxiv:hep-th/0405256)
-
Simon McNamara, Constantinos Papageorgakis, Sanyaje Ramgoolam, Bill Spence, Appendix A of: Finite effects on the collapse of fuzzy spheres, JHEP 0605:060, 2006 (arxiv:hep-th/0512145)
-
Simon McNamara, Section 4 of: Twistor Inspired Methods in Perturbative FieldTheory and Fuzzy Funnels, 2006 (spire:1351861, pdf, pdf)
-
Constantinos Papageorgakis, p. 161-162 of: On matrix D-brane dynamics and fuzzy spheres, 2006 (pdf)
As codes for holographic entanglement entropy
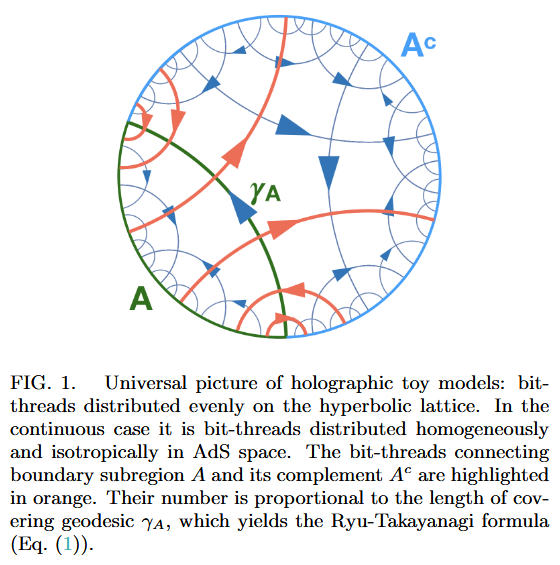
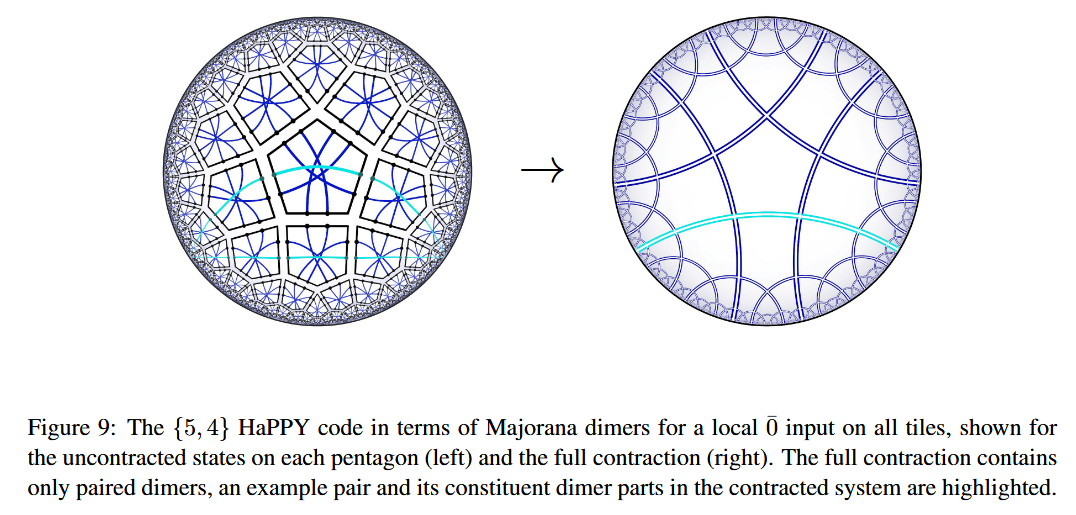
Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:
-
Alexander Jahn, Marek Gluza, Fernando Pastawski, Jens Eisert, Majorana dimers and holographic quantum error-correcting code, Phys. Rev. Research 1, 033079 (2019) (arXiv:1905.03268)
-
Han Yan, Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models, Phys. Rev. B 102, 161119 (2020) (arXiv:1911.01007)
For Dyson-Schwinger equations
Discussion of round chord diagrams organizing Dyson-Schwinger equations:
-
Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)
-
Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)
-
Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]
Review in:
- Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)
Other
Appearance of horizontal chord diagrams in discussion of neutrino interactions in supernovae:
- Duff Neill, Hanqing Liu, Joshua Martin, Alessandro Roggero: Scattering Neutrinos, Spin Models, and Permutations [arXiv:2406.18677]
On
(For more see the references at AdS3/CFT2.)
An exact correspondence of the symmetric orbifold CFT of Liouville theory with a string theory on is claimed in:
-
Lorenz Eberhardt, Matthias Gaberdiel, String theory on and the symmetric orbifold of Liouville theory (arXiv:1903.00421)
-
Lorenz Eberhardt, Matthias Gaberdiel, Strings on (arXiv:1904.01585)
-
Lorenz Eberhardt, Matthias Gaberdiel, Rajesh Gopakumar, Deriving the Correspondence (arXiv:1911.00378)
-
Andrea Dei, Lorenz Eberhardt, Correlators of the symmetric product orbifold (arXiv:1911.08485)
based on
- Shouvik Datta, Lorenz Eberhardt, Matthias Gaberdiel, Stringy holography for JHEP 1801 (2018) 146 (arXiv:1709.06393)
See also
-
Stefano Speziali, Spin 2 fluctuations in 1/4 BPS AdS3/CFT2 (arxiv:1910.14390)
-
Lorenz Eberhardt, at higher genus (arXiv:2002.11729)
-
Lorenz Eberhardt, Summing over Geometries in String Theory (arXiv:2102.12355)
On blackD6-D8-brane bound states in massive type IIA string theory, with defect D2-D4-brane bound states inside them realizing AdS3-CFT2 “inside” AdS7-CFT6:
-
Giuseppe Dibitetto, Nicolò Petri, 6d surface defects from massive type IIA, JHEP 01 (2018) 039 (arxiv:1707.06154)
-
Nicolò Petri, section 6.5 of: Supersymmetric objects in gauged supergravities (arxiv:1802.04733)
-
Nicolò Petri, Surface defects in massive IIA, talk at Recent Trends in String Theory and Related Topics 2018 (pdf)
-
Giuseppe Dibitetto, Nicolò Petri, vacua and surface defects in massive IIA (arxiv:1904.02455)
-
Yolanda Lozano, Niall T. Macpherson, Carlos Nunez, Anayeli Ramirez, BPS (arxiv:1909.09636)
-
Yolanda Lozano, Niall T. Macpherson, Carlos Nunez, Anayeli Ramirez, Two dimensional quivers dual to solutions in massive IIA (arxiv:1909.10510)
-
Yolanda Lozano, Niall T. Macpherson, Carlos Nunez, Anayeli Ramirez, solutions in massive IIA, defect CFTs and T-duality (arxiv:1909.11669)
-
Kostas Filippas, Non-integrability on supergravity (arxiv:1910.12981)
On blackD4-D8-brane bound states in massive type IIA string theory, with defect D2-D6-brane bound states inside them realizing AdS3-CFT2 “inside” AdS7-CFT6:
-
Giuseppe Dibitetto, Nicolò Petri, Surface defects in the D4 − D8 brane system, JHEP 01 (2019) 193 (arxiv:1807.07768)
-
Giuseppe Dibitetto, Nicolò Petri, vacua and surface defects in massive IIA (arxiv:1904.02455)
On
-
Igor Klebanov, Giuseppe Torri, M2-branes and AdS/CFT, Int.J.Mod.Phys.A25:332-350,2010 (arXiv:0909.1580)
-
Kazuo Hosomichi, M2-branes and AdS/CFT: A Review (arXiv:2003.13914)
-
Silvia Penati, Exact Results in AdS4/CFT3 (arXiv:2004.00841)
-
Manikantt Mummalaneni: AdS4/CFT3: ABJM Theory, Brane Geometry, Correlators and Mellin Space [arXiv:2408.11835]
On
-
Jorge Escobedo, Integrability in AdS/CFT: Exact Results for Correlation Functions, 2012 (spire:1264432)
Computing dual string scattering amplitudes by AdS/CFT beyond the planar limit:
- Luis Alday, Agnese Bissi, Eric Perlmutter, Genus-One String Amplitudes from Conformal Field Theory, JHEP06(2019) 010 (arXiv:1809.10670)
On
We list references specific to .
In
-
Edward Witten, Five-Brane Effective Action In M-Theory J. Geom. Phys.22:103-133,1997 (arXiv:hep-th/9610234)
-
Edward Witten, AdS/CFT Correspondence And Topological Field Theory JHEP 9812:012,1998 (arXiv:hep-th/9812012)
it is argued that the conformal blocks of the 6d (2,0)-superconformal QFT are entirely controled just by the effective 7d Chern-Simons theory inside 11-dimensional supergravity, but only the abelian piece is discussed explicitly.
The fact that this Chern-Simons term is in fact a nonabelian higher dimensional Chern-Simons theory in , due the quantum anomaly cancellation, is clear from the original source, equation (3.14) of
- Michael Duff, James Liu, Ruben Minasian, Eleven Dimensional Origin of String/String Duality: A One Loop Test (arXiv:hep-th/9506126)
but seems not to be noted explicitly in the context of before the references
-
H. Lü, Yi Pang, Seven-Dimensional Gravity with Topological Terms Phys.Rev.D81:085016 (2010) (arXiv:1001.0042)
-
H. Lu, Zhao-Long Wang, On M-Theory Embedding of Topologically Massive Gravity Int.J.Mod.Phys.D19:1197 (2010) (arXiv:1001.2349)
More on the relation between the M5-brane and supergravity on and arguments for the R-symmetry group on the 6d theory from the 7d theory are given in
- Alexei Nurmagambetov, I. Y. Park, On the M5 and the AdS7/CFT6 Correspondence, Phys. Lett. B524 (2002) 185-191 (arXiv:hep-th/0110192)
See also
- M. Nishimura, Y. Tanii, Local Symmetries in the Correspondence, Mod. Phys. Lett. A14 (1999) 2709-2720 (arXiv:hep-th/9910192)
Discussion of the in via conformal bootstrap:
-
Shai Chester, Bootstrapping M-theory, PhD thesis, Princeton (2018) [pdf, ark:88435/dsp01kw52jb833]
-
Nathan B. Agmon, Shai Chester, Silviu S. Pufu: Solving M-theory with the Conformal Bootstrap, J. High Energ. Phys. 2018 159 (2018). [arXiv:1711.07343, doi:10.1007/JHEP06(2018)159]
-
Shai Chester, Eric Perlmutter: M-Theory Reconstruction from CFT and the Chiral Algebra Conjecture, J. High Energ. Phys. 2018 116 (2018) [arXiv:1805.00892, doi:10.1007/JHEP08(2018)116]
-
Luis Alday, Shai Chester, Himanshu Raj, 6d and M-theory at 1-loop (arXiv:2005.07175)
In
- Ergin Sezgin, P. Sundell, Massless Higher Spins and Holography (hep-th/0205131)
arguments are given that the 7d theory is a higher spin gauge theory extension of .
Generalization beyond exact AdS / exact CFT
Discussion for cosmology of intersecting D-brane models (ambient anti de Sitter spacetimes with the conformal intersecting branes at the asymptotic boundary) includes the following (see also at Randall-Sundrum model):
-
Igor Klebanov, Matthew Strassler, Supergravity and a Confining Gauge Theory: Duality Cascades and -Resolution of Naked Singularities, JHEP 0008:052, 2000 (arXiv:hep-th/0007191)
-
Igor Klebanov, Edward Witten, Superconformal Field Theory on Threebranes at a Calabi-Yau Singularity, Nucl.Phys.B536:199-218, 1998 (arXiv:hep-th/9807080)
-
Nemanja Kaloper, Origami World, JHEP 0405 (2004) 061 (arXiv:hep-th/0403208)
-
Angel Uranga, section 18 of TASI lectures on String Compactification, Model Building, and Fluxes, 2005 (pdf)
-
Antonino Flachi, Masato Minamitsuji, Field localization on a brane intersection in anti-de Sitter spacetime, Phys.Rev.D79:104021, 2009 (arXiv:0903.0133)
-
Jiro Soda, AdS/CFT on the brane, Lect.Notes Phys.828:235-270, 2011 (arXiv:1001.1011)
-
Shunsuke Teraguchi, around slide 21 String theory and its relation to particle physics, 2007 (pdf)
-
Gianluca Grignani, Troels Harmark, Andrea Marini, Marta Orselli, The Born-Infeld/Gravity Correspondence, Phys. Rev. D 94, 066009 (2016) (arXiv:1602.01640)
pp-Waves as Penrose limits of spacetimes
Dedicated discussion of pp-wave spacetimes as Penrose limits (Inönü-Wigner contractions) of AdSp x S^q spacetimes and of the corresponding limit of AdS-CFT duality:
-
David Berenstein, Juan Maldacena, Horatiu Nastase, Section 2 of: Strings in flat space and pp waves from Super Yang Mills, JHEP 0204 (2002) 013 (arXiv:hep-th/0202021)
-
N. Itzhaki, Igor Klebanov, Sunil Mukhi, PP Wave Limit and Enhanced Supersymmetry in Gauge Theories, JHEP 0203 (2002) 048 (arXiv:hep-th/0202153)
-
Nakwoo Kim, Ari Pankiewicz, Soo-Jong Rey, Stefan Theisen, Superstring on PP-Wave Orbifold from Large-N Quiver Gauge Theory, Eur. Phys. J. C25:327-332, 2002 (arXiv:hep-th/0203080)
-
E. Floratos, Alex Kehagias, Penrose Limits of Orbifolds and Orientifolds, JHEP 0207 (2002) 031 (arXiv:hep-th/0203134)
-
E. M. Sahraoui, E. H. Saidi, Metric Building of pp Wave Orbifold Geometries, Phys.Lett. B558 (2003) 221-228 (arXiv:hep-th/0210168)
Review:
-
Darius Sadri, Mohammad Sheikh-Jabbari, The Plane-Wave/Super Yang-Mills Duality, Rev. Mod. Phys. 76:853, 2004 (arXiv:hep-th/0310119)
-
Badis Ydri, Section 3.1.10 of: Review of M(atrix)-Theory, Type IIB Matrix Model and Matrix String Theory (arXiv:1708.00734), published as: Matrix Models of String Theory, IOP 2018 (ISBN:978-0-7503-1726-9)
See also:
- Michael Gutperle, Nicholas Klein, A Penrose limit for type IIB solutions (arXiv:2105.10824)
Applications to physics
To gravity
Discussion of event horizons of black holes in terms of AdS/CFT (the “firewall problem”) is in
- Kyriakos Papadodimas, Suvrat Raju, An Infalling Observer in AdS/CFT (arXiv:1211.6767)
To black hole interiors:
- Juan Maldacena, Toy models for black holes II, talk at PiTP 2018 From QBits to spacetime (recording)
The SYK model gives us a glimpse into the interior of an extremal black hole…That’s the feature of SYK that I find most interesting…It is a feature this model has, that I think no other model has
To symmetries in gravity:
- Daniel Harlow, Hirosi Ooguri, Constraints on symmetry from holography, Phys. Rev. Lett. 122, 191601, 2019 (arXiv:1810.05337, doi:10.1103/PhysRevLett.122.191601)
To the quark-gluon plasma
Applications of AdS-CFT to the quark-gluon plasma of QCD:
Expositions and reviews:
-
Pavel Kovtun, Quark-Gluon Plasma and String Theory, RHIC news (2009) (blog entry)
-
Makoto Natsuume, String theory and quark-gluon plasma (arXiv:hep-ph/0701201)
-
Steven Gubser, Using string theory to study the quark-gluon plasma: progress and perils (arXiv:0907.4808)
-
Francesco Biagazzi, A. l. Cotrone, Holography and the quark-gluon plasma, AIP Conference Proceedings 1492, 307 (2012) (doi:10.1063/1.4763537, slides pdf)
-
Brambilla et al., section 9.2.2 of QCD and strongly coupled gauge theories - challenges and perspectives, Eur Phys J C Part Fields. 2014; 74(10): 2981 (arXiv:1404.3723, doi:10.1140/epjc/s10052-014-2981-5)
Holographic discussion of the shear viscosity of the quark-gluon plasema goes back to
- Giuseppe Policastro, D.T. Son, A.O. Starinets, Shear viscosity of strongly coupled N=4 supersymmetric Yang-Mills plasma, Phys. Rev. Lett.87:081601, 2001 (arXiv:hep-th/0104066)
Other original articles include:
-
Hovhannes R. Grigoryan, Paul M. Hohler, Mikhail A. Stephanov, Towards the Gravity Dual of Quarkonium in the Strongly Coupled QCD Plasma (arXiv:1003.1138)
-
Brett McInnes, Holography of the Quark Matter Triple Point (arXiv:0910.4456)
To particle physics
- Joseph Polchinski, Matthew Strassler, Hard Scattering and Gauge/String Duality, Phys. Rev. Lett. 88:031601, 2002, (arXiv:hep-th/0109174)
For more see at AdS/QCD correspondence.
To fluid dynamics
Application to fluid dynamics – see also at fluid/gravity correspondence:
- Sayantani Bhattacharyya, Veronika Hubeny, Shiraz Minwalla, Mukund Rangamani, Nonlinear Fluid Dynamics from Gravity, JHEP 0802:045, 2008 (arXiv:0712.2456)
To condensed matter physics
On AdS-CFT in condensed matter physics:
Textbook account
- Sean Hartnoll, Andrew Lucas, Subir Sachdev, Holographic quantum matter, MIT Press 2018 (arXiv:1612.07324, publisher)
Further reviews include the following:
-
A S T Pires, Ads/CFT correspondence in condensed matter (arXiv:1006.5838)
-
Subir Sachdev, Condensed matter and AdS/CFT (arXiv:1002.2947)
-
Yuri V. Kovchegov, AdS/CFT applications to relativistic heavy ion collisions: a brief review (arXiv:1112.5403)
-
Alberto Salvio, Superconductivity, Superfluidity and Holography (arXiv:1301.0201)
-
Holography and Extreme Chromodynamics, Santiago de Compostela, July 2018
On holographic superconductors via AdS4/CFT3 duality (hence with the bulk theory being 11d supergravity aka M-theory):
The original article (according to ZLSS15, p. ix), regarding AdS4/CFT3-duality (hence with the bulk theory being 11d supergravity, whence “M-theory”) as a tool for understanding strongly coupled condensed matter physics (specifically superconductivity):
- Christopher P. Herzog, Pavel Kovtun, Subir Sachdev, Dam Thanh Son, Quantum critical transport, duality, and M-theory, Phys. Rev. D 75 (2007) 085020 [arXiv:hep-th/0701036, doi:10.1103/PhysRevD.75.085020]
and further discussion:
-
Jerome P. Gauntlett, Julian Sonner, Toby Wiseman: Holographic superconductivity in M-Theory, Phys. Rev. Lett. 103 (2009) 151601 [arXiv:0907.3796, doi:10.1103/PhysRevLett.103.151601]
-
Steven S. Gubser, Silviu S. Pufu, Fabio D. Rocha: Quantum critical superconductors in string theory and M-theory, Phys. Lett. B 683 (2010) 201-204 [arXiv:0908.0011, doi:10.1016/j.physletb.2009.12.017]
-
Jerome Gauntlett, Julian Sonner, Toby Wiseman: Quantum Criticality and Holographic Superconductors in M-theory, J. High Energ. Phys. 2010 60 (2010) [arXiv:0912.0512, doi:10.1007/JHEP02(2010)060]
-
Aristomenis Donos, Jerome P. Gauntlett, Julian Sonner, Benjamin Withers: Competing orders in M-theory: superfluids, stripes and metamagnetism, J. High Energ. Phys. 2013 108 (2013) [arXiv:1212.0871, doi:10.1007/JHEP03(2013)108]
-
Aristomenis Donos, Jerome P. Gauntlett, Christiana Pantelidou: Semi-local quantum criticality in string/M-theory, J. High Energ. Phys. 2013 103 (2013) [doi:10.1007/JHEP03(2013)103, arXiv:1212.1462]
-
Yu-Sen An, Li Li, Fu-Guo Yang, Run-Qiu Yang: Interior Structure and Complexity Growth Rate of Holographic Superconductor from M-Theory, J. High Energ. Phys. 2022 133 (2022) [arXiv:2205.02442, doi:10.1007/JHEP08(2022)133]
Applications in mathematics
To the volume conjecture
Suggestion that the statement of the volume conjecture is really AdS-CFT duality combined with the 3d-3d correspondence for M5-branes wrapped on hyperbolic 3-manifolds:
-
Dongmin Gang, Nakwoo Kim, Sangmin Lee, Section 3.2_Holography of 3d-3d correspondence at Large , JHEP04(2015) 091 (arXiv:1409.6206)
-
Dongmin Gang, Nakwoo Kim, around (21) of: Large twisted partition functions in 3d-3d correspondence and Holography, Phys. Rev. D 99, 021901 (2019) (arXiv:1808.02797)
To deep learning in neural networks
On the deep learning algorithm on neural networks as analogous to the AdS/CFT correspondence:
-
Yi-Zhuang You, Zhao Yang, Xiao-Liang Qi, Machine Learning Spatial Geometry from Entanglement Features, Phys. Rev. B 97, 045153 (2018) (arxiv:1709.01223)
-
W. C. Gan and F. W. Shu, Holography as deep learning, Int. J. Mod. Phys. D 26, no. 12, 1743020 (2017) (arXiv:1705.05750)
-
J. W. Lee, Quantum fields as deep learning (arXiv:1708.07408)
-
Koji Hashimoto, Sotaro Sugishita, Akinori Tanaka, Akio Tomiya, Deep Learning and AdS/CFT, Phys. Rev. D 98, 046019 (2018) (arxiv:1802.08313)
Philosophy of AdS/CFT
- Radin Dardashti, Richard Dawid, Sean Gryb, Karim Thébault (2020). On the Empirical Consequences of the AdS/CFT Duality. In Nick Huggett, Keizo Matsubara, and Christian Wüthrich (Eds.), Beyond Spacetime: The Foundations of Quantum Gravity (pp. 284-303). Cambridge: Cambridge University Press. (doi:10.1017/9781108655705.016, arXiv:1810.00949)
Last revised on March 8, 2025 at 15:19:16. See the history of this page for a list of all contributions to it.