nLab
Kan extension

Idea

The Kan extension of a functor $F:C\to D$ with respect to a functor

$$\begin{array}{c}C\\ {\downarrow }^p\\ C\prime \end{array}$$\array{ C \\ \downarrow^p \\ C' }

is, if it exists, a kind of best approximation to the problem of finding a functor $C\prime \to D$ such that

$$\begin{array}{ccc}C& \stackrel{F}{\to }& D\\ {\downarrow }^p& \nearrow \\ C\prime \end{array},$$\array{ C &\stackrel{F}{\to}& D \\ \downarrow^p & \nearrow \\ C' } \,,

hence to extending the domain of $F$ through $p$ from $C$ to $C\prime$.

More generally, this makes sense not only in Cat but in any 2-category.

Similarly, a Kan lift is the best approximation to lifting a morphism $F:C\to D$ through a morphism

$$\begin{array}{c}D\prime \\ \downarrow \\ D\end{array}$$\array{ D' \\ \downarrow \\ D }

to a morphism $\hat{F}$

$$\begin{array}{ccc}& & D\prime \\ & {}^{\hat{F}}\nearrow & \downarrow \\ C& \stackrel{F}{\to }& D\end{array}.$$\array{ && D' \\ & {}^{\hat F}\nearrow & \downarrow \\ C &\stackrel{F}{\to}& D } \,.

Kan extensions are ubiquitous. See the discussion at Examples below.

Definitions

There are various slight variants of the definition of Kan extension . In good cases they all exist and all coincide, but in some cases only some of these will actually exist.

We (have to) distinguish the following cases:

1. “ordinary” or “weak” Kan extensions

   These define the extension of an entire functor, by an adjointness relation.

   Here we (have to) distinguish further between

   1. global Kan extensions,

      which define extensions of all possible functors of given domain and codomain (if all of them indeed exist);

   2. local Kan extensions,

      which define extensions of single functors only, which may exist even if not every functor has an extension.

2. “pointwise” or “strong” Kan extensions

   These define the value of an extended functor on each object (each “point”) by a weighted (co)limit.

   Furthermore, a pointwise Kan extension can be “absolute”.

If the pointwise version exists, then it coincides with the “ordinary” or “weak” version, but the former may exist without the pointwise version existing. See below for more.

Some authors (such as Kelly) assert that only pointwise Kan extensions deserve the name “Kan extension,” and use the term as “weak Kan extension” for a functor equipped with a universal natural transformation. It is certainly true that most Kan extensions which arise in practice are pointwise. This distinction is even more important in enriched category theory.

Ordinary or weak Kan extensions

Global Kan extensions

Let

$$p:C\to C\prime$$p : C \to C'

be a functor. For $D$ any other category, write

$$p^{*}:[C\prime ,D]\to [C,D]$$p^* : [C',D] \to [C,D]

for the induced functor on the functor categories: this sends a functor $h:C\prime \to D$ to the composite functor $p^{*}h:C\stackrel{p}{\to }C\prime \stackrel{h}{\to }D$.

Definition

If $p^{*}$ has a left adjoint, typically denoted

$$p_{!}:[C,D]\to [C\prime ,D]$$p_! : [C,D] \to [C',D]

or

$${\mathrm{Lan}}_p:[C,D]\to [C\prime ,D]$$Lan_p : [C,D] \to [C',D]

then this left adjoint is called the ( ordinary or weak ) left Kan extension operation along $p$. For $h\in [C,D]$ we call $p_{!}h$ the left Kan extension of $h$ along $p$.

Similarly, if $p^{*}$ has a right adjoint, this right adjoint is called the right Kan extension operation along $p$. It is typically denoted

$$p_{*}:[C,D]\to [C\prime ,D]$$p_* : [C,D] \to [C',D]

or

$$\mathrm{Ran}={\mathrm{Ran}}_p:[C,D]\to [C\prime ,D].$$Ran = Ran_p: [C,D] \to [C',D] \,.

The analogous definition clearly makes sense as stated in other contexts, such as in enriched category theory.

Observation

If $C\prime =*$ is the terminal category, then

• the left Kan extension operation forms the colimit of a functor;

• the right Kan extension operation forms the limit of a functor.

Proof

The functor $p^{*}$ in this case sends objects $d$ of $D$ to the constant functor ${\Delta }_d$ on $d$. Notice that for $F\in [C,D]$ any functor,

• a natural transformation ${\Delta }_d\to F$ is the same as a cone over $F$;

• a natural transformation $F\to {\Delta }_d$ is the same as a cocone under $F$.

Therefore the natural hom-isomorphisms of the adjoint functors $(p_{!}⊣p^{*})$ and $(p^{*}⊣p_{*})$

$$D(d,p_{*}F)\simeq \mathrm{Func}({\Delta }_d,F)$$D(d, p_* F) \simeq Func(\Delta_d, F)

and

$$D(p_{!}F,d)\simeq \mathrm{Func}(F,{\Delta }_d)$$D(p_! F, d) \simeq Func(F, \Delta_d)

assert that

• $p_{*}F$ corepresents the cones over $F$: this means by definition that $p_{*}F={\lim }_{\leftarrow }F$ is the limit over $F$;

• $p_{!}F$ represents the cocones under $F$: this means by definition that $p_{!}F={\lim }_{\to }F$ is the colimit of $F$.

Local Kan extension

There is also a local definition of “the Kan extension of a given functor $F$ along $p$” which can exist even if the entire functor defined above does not. This is a generalization of the fact that a particular diagram of shape $C$ can have a limit even if not every such diagram does. It is also a special case of the fact discussed at adjoint functor that an adjoint functor can fail to exist completely, but may still be partially defined. If the local Kan extension of every single functor exists for some given $p:C\to C\prime$ and $D$, then these local Kan extensions fit together to define a functor which is the global Kan extension.

Thus, by the general notion of “partial adjoints”; we say

Definition

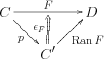
The local left Kan extension of a functor $F\in [C,D]$ along $p:C\to C\prime$* is, if it exists, a functor

$${\mathrm{Lan}}_{p}F:C\prime \to D$$Lan_p\,F : C'\to D

equipped with a natural isomorphism

$${\mathrm{Hom}}_{[C,D]}(F,p^{*}(-))\cong {\mathrm{Hom}}_{[C\prime ,D]}({\mathrm{Lan}}_{p}F,-),$$Hom_{[C,D]}(F,p^*(-))\cong Hom_{[C',D]}(Lan_p\,F,-) \,,

hence a (co)representation of the functor ${\mathrm{Hom}}_{[C,D]}(F,p^{*}(-))$.

The local definition of right Kan extensions along $p$ is dual.

As for adjoints and limits, by the usual logic of representable functors this can equivalently be rephrased in terms of universal morphisms:

Definition

The left Kan extension $\mathrm{Lan}F={\mathrm{Lan}}_{p}F$ of $F:C\to D$ along $p:C\to C\prime$ is a functor $\mathrm{Lan}F:C\prime \to D$ equipped with a natural transformation ${\eta }_F:F\Rightarrow p^{*}\mathrm{Lan}F$.

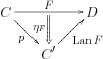
with the property that every other natural transformation $F\Rightarrow p^{*}G$ factors uniquely through ${\eta }_F$ as

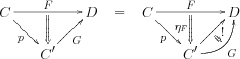
Similarly for the right Kan extension, with the direction of the natural transformations reversed:

By the usual reasoning (see e.g. Categories Work, chapter IV, theorem 2), if these representations exist for every $F$ then they can be organised into a left (right) adjoint ${\mathrm{Lan}}_p$ (${\mathrm{Ran}}_p$) to $p^{*}$.

Remark

The definition in this form makes sense not just in Cat but in every 2-category. In slightly different terminology, the left Kan extension of a 1-cell $F:C\to D$ along a 1-cell $p\in K(C,C\prime )$ in a 2-category $K$ is a pair $({\mathrm{Lan}}_{p}F,\alpha )$ where $\alpha :F\to {\mathrm{Lan}}_{p}F\circ p$ is a 2-cell which reflects the object $F\in K(C,D)$ along the functor $p^{*}=K(p,D):K(C\prime ,D)\to K(C,D)$. Equivalently, it is such a pair such that for every $G:C\prime \to D$, the function

$$K(C\prime ,D)({\mathrm{Lan}}_{p}F,G)\stackrel{-\cdot \alpha }{\to }K(C,D)(F,G\circ p)$$K(C',D)(Lan_p F, G) \xrightarrow{- \cdot \alpha} K(C,D)(F, G \circ p)

is a bijection.

In this form, the definition generalizes easily to any n-category for any $n\ge 2$. If $K$ is an $n$-category, we say that the left Kan extension of a 1-morphism $F:C\to D$ along a 1-morphism $p\in K(C,C\prime )$ is a pair $({\mathrm{Lan}}_{p}F,\alpha )$, where ${\mathrm{Lan}}_{p}F:C\prime \to D$ is a 1-morphism and $\alpha :F\to {\mathrm{Lan}}_{p}F\circ p$ is a 2-morphism, with the property that for any 1-morphism $G:C\prime \to D$, the induced functor

$$K(C\prime ,D)({\mathrm{Lan}}_{p}F,G)\stackrel{-\cdot \alpha }{\to }K(C,D)(F,G\circ p)$$K(C',D)(Lan_p F, G) \xrightarrow{- \cdot \alpha} K(C,D)(F, G \circ p)

is an equivalence of $(n-2)$-categories.

Preservation of Kan extensions

We say that a Kan extension ${\mathrm{Lan}}_{p}F$ is preserved by a functor $G$ if the composite $G\circ {\mathrm{Lan}}_{p}F$ is a Kan extension of $GF$ along $p$, and moreover the universal natural transformation $GF\to G({\mathrm{Lan}}_{p}F)p$ is the composite of $G$ with the universal transformation $F\to ({\mathrm{Lan}}_{p}F)f$.

Pointwise or strong Kan extensions

If the codomain category $D$ admits certain (co)limits, then left and right Kan extensions can be constructed, over each object (“point”) of the domain category $C\prime$ out of these: Kan extensions that admit this form are called pointwise .

The notion of pointwise Kan extensions deserves to be discussed in the general context of enriched category theory, which we do below. The reader may want to skip ahead to the section

• pointwise Kan extensions by conical (co)limits

which discusses the situation in ordinary (Set-enriched) category theory in terms of ordinary limits (“conical” limits, defined in terms of cones, to be distinguished from the more general weighted limits). While the formulas in that case are classical and fundamentally useful in practice, they do rely heavily on special properties of the enriching category Set.

The general formulation of pointwise Kan extensions in general enriched contexts is

• in terms of weighted (co)limits.

In the case that the codomain category is (co)tensored these may be expressed equivalently

• in terms of (co)ends.

First, here is a characterization that doesn’t rely on any computational framework:

Definition

A Kan extension, def. 2, is called pointwise if and only if it is preserved by all representable functors.

(Categories Work, theorem X.5.3)

in terms of weighted (co)limits

Suppose given $F:C\to D$ and $p:C\to C\prime$ such that for every $c\prime \in C\prime$, the weighted limit

$$({\mathrm{Ran}}_{p}F)(c\prime )≔{\lim }^{C\prime (c\prime ,p(-))}F.$$(Ran_p F)(c') \coloneqq lim^{C'(c',p(-))} F \,.

exists. Then these objects fit together into a functor ${\mathrm{Ran}}_{p}F$ which is a right Kan extension of $F$ along $p$. Dually, if the weighted colimit

$$({\mathrm{Lan}}_{p}F)(c\prime )≔{\mathrm{colim}}^{C\prime (p(-),c\prime )}F.$$(Lan_p F)(c') \coloneqq colim^{C'(p(-),c')} F \,.

exists for all $c\prime$, then they fit together into a left Kan extension ${\mathrm{Lan}}_{p}F$. These definitions evidently make sense in the generality of $V$-enriched category theory for $V$ a closed symmetric monoidal category. (In fact, they can be modified slightly to make sense in the full generality of a 2-category equipped with proarrows.)

In particular, this means that if $C$ is small and $D$ is complete (resp. cocomplete), then all right (resp. left) Kan extensions of functors $F:C\to D$ exist along any functor $p:C\to C\prime$.

One can prove that any Kan extension constructed in this way must be pointwise, in the sense of being preserved by all representables as above. Moreover, conversely, if a Kan extension ${\mathrm{Lan}}_{p}F$ is pointwise, then one can prove that $({\mathrm{Lan}}_{p}F)(c\prime )$ must be in fact a $C\prime (p(-),c\prime )$-weighted colimit of $F$, and dually; thus the two notions are equivalent.

in terms of (co)ends

If the $V$-enriched category $D$ is powered over $V$, then the above weighted limit may be re-expressed in terms of an end as

$$({\mathrm{Ran}}_{p}F)(c\prime )\simeq {\int }_{c\in C}C\prime (c\prime ,p(c))⋔F(c).$$(Ran_p F)(c') \simeq \int_{c \in C} C'(c',p(c))\pitchfork F(c) \,.

So in particular when $D=V$ this is

$$({\mathrm{Ran}}_{p}F)(c\prime )\simeq {\int }_{c\in C}[C\prime (c\prime ,p(c)),F(c)].$$(Ran_p F)(c') \simeq \int_{c \in C} [C'(c',p(c)),F(c)] \,.

Similarly, if $D$ is tensored over $V$, then the left Kan extension is given by a coend.

$$({\mathrm{Lan}}_{p}F)(c\prime )\simeq {\int }^{c\in C}C\prime (p(c),c\prime )\otimes F(c).$$(Lan_p F)(c') \simeq \int^{c \in C} C'(p(c),c')\otimes F(c) \,.

in terms of conical (co)limits

In the case of functors between ordinary locally small categories, hence in the special case of $V$-enriched category theory for $V=$ Set, there is an expression of a weighted (co)limit and hence a pointwise Kan extension as an ordinary (“conical”, meaning: in terms of cones) (co)limit over a comma category:

Proposition

Let

• $C$ be a small category;

• $D$ have all small limits.

Then the right Kan extension of a functor $F:C\to D$ of locally small categories along a functor $p:C\to C\prime$ exists and its value on an object $c\prime \in C\prime$ is given by the limit

$$({\mathrm{Ran}}_{p}F)(c\prime )\simeq \underleftarrow{\lim }(({\Delta }_{c\prime }/p)\to C\stackrel{F}{\to }D),$$(Ran_p F)(c') \simeq \lim_\leftarrow \left((\Delta_{c'}/p) \to C \stackrel{F}{\to} D\right) \,,

where

• ${\Delta }_{c\prime }/p$ is the comma category;

• ${\Delta }_{c\prime }/p\to C$ is the canonical forgetful functor.

Likewise, if $D$ admits small colimits, the left Kan extension of a functor exists and is pointwise given by the colimit

$$({\mathrm{Lan}}_{p}F)(c\prime )\simeq \underrightarrow{\lim }((p/{\Delta }_{c\prime })\to C\stackrel{F}{\to }D).$$(Lan_p F)(c') \simeq \lim_\to \left((p/\Delta_{c'}) \to C \stackrel{F}{\to} D\right) \,.

This appears for instance as (Borceux, I, thm 3.7.2). Discussion in the context of enriched category theory is in (Kelly, section 3.4).

A cartoon picture of the forgetful functor out of the comma category $p/{\Delta }_{c\prime }\to C$, useful to keep in mind, is

$$\left(\begin{array}{ccccc}p(c_1)& & \stackrel{p(\varphi )}{\to }& & p(c_2)\\ & \searrow & & \swarrow \\ & & c\prime \end{array}\right)\mapsto \left(c_1\stackrel{\varphi }{\to }{c}_2\right).$$\left( \array{ p(c_1) &&\stackrel{p(\phi)}{\to}&& p(c_2) \\ & \searrow && \swarrow \\ && c' } \right) \;\; \mapsto \;\; \left( c_1 \stackrel{\phi}{\to} c_2 \right) \,.

The comma category here is equivalently the category of elements of the functor $C\prime (p(-),c\prime ):C^{\mathrm{op}}\to \mathrm{Set}$

$$(p/{\Delta }_{c\prime })\simeq \mathrm{el}(C\prime (p(-),c\prime )).$$(p/\Delta_{c'}) \simeq el( C'(p(-), c') ) \,.

Proof

Consider the case of the left Kan extension, the other case works analogously, but dually.

First notice that the above pointwise definition of values of a functor canonically extends to an actual functor:

for $\varphi :c{\prime }_1\to c{\prime }_2$ any morphism in $C\prime$ we get a functor

$${\varphi }_{*}:p/{\Delta }_{c{\prime }_1}\to p/{\Delta }_{c{\prime }_2}$$\phi_* : p/\Delta_{c'_1} \to p/\Delta_{c'_2}

of comma categories, by postcomposition. This morphism of diagrams induces canonically a corresponding morphism of colimits

$$({\mathrm{Lan}}_{p}F)(c{\prime }_1)\to ({\mathrm{Lan}}_{p}F)(c{\prime }_2).$$(Lan_p F)(c'_1) \to (Lan_p F)(c'_2) \,.

Now for the universal property of the functor ${\mathrm{Lan}}_{p}F$ defined this way. For $c\prime \in C\prime$ denote the components of the colimiting cocone $({\mathrm{Lan}}_{p}F)(c\prime ):={\lim }_{\to }(p/{\Delta }_{c\prime }\to C\stackrel{F}{\to }D)$ by $s_{(-)}$, as in

$$\begin{array}{ccccc}(p(c_1)\stackrel{\varphi }{\to }c\prime )& & \stackrel{p(h)}{\to }& & (p(c_2)\stackrel{\lambda }{\to }c\prime )\\ \\ \\ F(c_1)& & \stackrel{F(h)}{\to }& & F(c_2)\\ & {}_{s_{\varphi }}\searrow & & {\swarrow }_{s_{\lambda }}\\ & & ({\mathrm{Lan}}_{p}F)(c\prime )\end{array}.$$\array{ (p(c_1)\stackrel{\phi}{\to} c') &&\stackrel{p(h)}{\to}&& (p(c_2)\stackrel{\lambda}{\to} c') \\ \\ \\ F(c_1) &&\stackrel{F(h)}{\to}&& F(c_2) \\ & {}_{\mathllap{s_\phi}}\searrow && \swarrow_{\mathrlap{s_{\lambda}}} \\ && (Lan_p F)(c') } \,.

We now construct in components a natural transformation

$${\eta }_F:F\to p^{*}{\mathrm{Lan}}_{p}F$$\eta_F : F \to p^* Lan_p F

for ${\mathrm{Lan}}_{p}F$ defined as above, and show that it satisfies the required universal property. The components of ${\eta }_F$ over $c\in C$ are morphisms

$${\eta }_F(c):F(c)\to ({\mathrm{Lan}}_{p}F)(p(c)).$$\eta_F(c) : F(c) \to (Lan_p F)(p (c)) \,.

Take these to be given by

$${\eta }_F(c):=s_{{\mathrm{Id}}_{p(c)}}$$\eta_F(c) := s_{Id_{p(c)}}

(this is similar to what happens in the proof of the Yoneda lemma, all of these arguments are variants of the argument for the Yoneda lemma, and vice versa). It is straightforward, if somewhat tedious, to check that these are natural, and that the natural transformation defined this way has the required universal property.

Comparing the definitions

We have seen that if $D$ has enough limits or colimits, then a pointwise Kan extension can be defined in terms of these limits, and will necessarily satisfy the universal property described first. However, not all Kan extensions are pointwise: that is, having a universal transformation $F\to ({\mathrm{Lan}}_{p}F)p$ does not necessarily imply that the individual values of ${\mathrm{Lan}}_{p}F$ are limits or colimits in its codomain. Non-pointwise Kan extensions can exist even when $D$ does not admit very many limits.

It should be noted, though, that pointwise Kan extensions can still exist, and hence the particular requisite limits/colimits exist, even if $D$ is not (co)complete. For instance, the Kan extensions that arise in the study of derived functors are pointwise, and in fact absolute (preserved by all functors), even though their codomains are homotopy categories which generally do not admit all limits and colimits.

Non-pointwise Kan extensions seem to be very rare in practice. However, the abstract notion of Kan extension (sometimes called simply “extension”) in a 2-category, and its dual notion of lifting, can be useful in 2-category theory. For instance, bicategories such as Prof admit all right extensions and right liftings; a bicategory with this property may be considered a horizontal categorification of a closed monoidal category.

Absolute Kan extensions

Am absolute Kan extension ${\mathrm{Lan}}_{p}F$ is one which is preserved by all functors $G$ out of the codomain of $f$:

(1)$$G({\mathrm{Lan}}_{p}F)\simeq {\mathrm{Lan}}_p(GF)$$G (Lan_p F) \simeq Lan_p(G F)

(same for right Kan extensions).

The most prominent example of absolute Kan extensions is given by adjoint functors; in fact they can be defined as certain absolute Kan extensions. See there for the precise statement.

absolute vs pointwise

Absolute Kan extensions are always pointwise, as the later can be defined as those preserved by representables; there are (lots of) examples of pointwise Kan extensions which are not absolute.

Note that in a general 2-category, absolute Kan extensions make perfect sense, while for defining pointwise ones more structure is needed: comma objects and/or some structure which would let us work with (co)limits inside that 2-category (such as a (co)Yoneda structure? or a proarrow equipment).

Of $(\mathrm{\infty },1)$-functors

The global definition of Kan extensions for functors in terms of left/right adjoints to pullbacks may be interpreted essentially verbatim in the context of (∞,1)-categories

See at (∞,1)-Kan extension.

In a general 2-category

The Kan extension of a functor may be regarded more abstractly as an extension-problem in the 2-category Cat of categories. The same extension problem can be stated verbatim in any 2-category and hence there is a corresponding more general notion of Kan extensions of 1-morphisms in 2-categories.

This is discussed in (Lack 09, section 2.2).

Properties

Left Kan extension on representables / fully faithfulness

Let $𝒱$ be a suitable enriching category (a cosmos). Notably $𝒱$ may be Set.

Proposition

For $F:C\to D$ a $𝒱$-enriched functor between small $𝒱$-enriched categories we have

1. the left Kan extension along $F$ takes representable presheaves $C(c,-):C\to 𝒱$ to their image under $F$:

   $${\mathrm{Lan}}_{F}C(c,-)\simeq D(F(c),-)$$Lan_F C(c, -) \simeq D(F(c), -)

   for all $c\in C$.

2. if $F$ is a full and faithful functor then $F^{*}({\mathrm{Lan}}_{F}H)\simeq H$ and in fact the $({\mathrm{Lan}}_F⊣F^{*})$-unit of an adjunction is a natural isomorphism

   $$\mathrm{Id}\stackrel{\simeq }{\to }{F}^{*}\circ {\mathrm{Lan}}_F$$Id \stackrel{\simeq}{\to} F^* \circ Lan_{F}

   whence it follows (see the basic properties of adjoint functors) that ${\mathrm{Lan}}_F:[C,𝒱]\to [D,𝒱]$ is itself a full and faithful functor.

The second statement appears for instance as (Kelly, prop. 4.23).

Proof

For the first statement, using the coend formula for the left Kan extension we have naturally in $d\prime \in D$ the expression

$$\begin{array}{rl}{\mathrm{Lan}}_{F}C(c,-):d\prime \mapsto & {\int }^{c\prime \in C}D(F(c\prime ),d\prime )\cdot C(c,-)(c\prime )\\ & \simeq {\int }^{c\prime \in C}D(F(c\prime ),d\prime )\cdot C(c,c\prime )\\ & \simeq D(F(c),d\prime )\end{array}.$$\begin{aligned} Lan_F C(c,-) : d' \mapsto & \int^{c' \in C} D(F(c'), d') \cdot C(c,-)(c') \\ & \simeq \int^{c' \in C} D(F(c'), d') \cdot C(c,c') \\ & \simeq D(F(c), d') \end{aligned} \,.

Here the last step is called sometimes the co-Yoneda lemma. It follows for instance by observing that ${\int }^{c\prime \in C}D(F(c\prime ),d\prime )\cdot C(c,c\prime )$ is equivalently dually the expression for the left Kan extension of the non-representable $D(F(-),d\prime ):C^{\mathrm{op}}\to 𝒱$ along the identity functor.

Similarly for the second, if $H:D\to E$ is any $𝒱$-enriched functor with $E$ tensored over $𝒱$, then its left Kan extension evaluated on the image of $F$ is

$$\begin{array}{rl}{\mathrm{Lan}}_{F}H:F(d)\mapsto & {\int }^{c\in C}D(F(c),F(d))\cdot H(c)\\ & \simeq {\int }^{c\in C}C(c,d)\cdot H(c)\\ & \simeq H(d)\end{array}.$$\begin{aligned} Lan_F H : F(d) \mapsto & \int^{c \in C} D(F(c), F(d)) \cdot H(c) \\ & \simeq \int^{c \in C} C(c, d) \cdot H(c) \\ & \simeq H(d) \end{aligned} \,.

Left Kan extensions preserving certain limits

See

(Borceux-Day)

(Karazeris-Protsonis).

Kan extension along (op)fibration

Proposition

Let $f:C\to D$ be a small opfibration of categories, and let $𝒞$ be a category with all small colimits. Then for each $d\in D$ the inclusion

$$f^{-1}(d)\to f/d$$f^{-1}(d) \to f/d

of the fiber over $d$ into the comma category given by

$$c\mapsto (c,{\mathrm{Id}}_d={\mathrm{Id}}_{f(c)})$$c \mapsto (c, Id_{d} = Id_{f(c)})

has a left adjoint, given by

$$(c,f(c)\to d)\mapsto c.$$(c, f(c) \to d) \mapsto c \,.

Therefore (by the discussion here) it is a cofinal functor. Accordingly, the local formula for the left Kan extension

$$f_{!}:[C,𝒟]\to [D,𝒟]$$f_! : [C, \mathcal{D}] \to [D, \mathcal{D}]

is equivalently given by taking the colimit over the fiber:

$$f_{!}X:d\mapsto \underset{\underset{f^{-1}(d)}{\to }}{\lim }X.$$f_! X : d \mapsto \lim_{\underset{f^{-1}(d)}{\to}} X \,.

Examples

The central point about examples of Kan extensions is:

Kan extensions are ubiquitous .

To a fair extent, category theory is all about Kan extensions and the other universal constructions: limits, adjoint functors, representable functors, which are all special cases of Kan extensions – and Kan extensions are special cases of these.

Listing examples of Kan extensions in category theory is much like listing examples of integrals in analysis: one can and does fill books with these. (In fact, that analogy has more to it than meets the casual eye: see coend for more).

Keeping that in mind, we do list some special cases and special classes of examples that are useful to know. But any list is necessarily wildly incomplete.

General

• For $C\prime =$ the point, the right Kan extension of $F$ is the limit of $F$, $\mathrm{Ran}F\simeq \lim F$ and the left Kan extension is the colimit $\mathrm{Lan}F\simeq \mathrm{colim}F$.

• For $f:X\to Y$ a morphism of sites coming from a functor $f^t:S_Y\to S_X$ of the underlying categories, the left Kan extension of functors along $f^t$ is the inverse image operation $f^{-1}:\mathrm{PSh}(Y)\to \mathrm{PSh}(X)$.

• see also examples of Kan extensions

Non-pointwise Kan extensions

We discuss examples of Kan extensions that are not point-wise

• Borceux, Handbook of Categorical Algebra I exercise 3.9.7

Restriction and extension of sheaves

For more on the following see also

• restriction and extension of sheaves

The basic example for left Kan extensions using the above pointwise formula, is in the construction of the pullback of sheaves along a morphism of topological spaces. Let $f:X\to Y$ be a continuous map and $F$ a presheaf over $X$. Then the formula $(f_{*}F)(U)=F(f^{-1}(U))$ clearly defines a presheaf $f_{*}F$ on $Y$, which is in fact a sheaf if $F$ is. On the other hand, given a presheaf $G$ over $Y$ we can not define pullback presheaf $(f^{-1}G)(V)=G(f(V))$ because $f(V)$ might not be open in general (unless $f$ is an open map). For Grothendieck sites such $f(V)$ would not make even sense. But one can consider approximating from above by $G(W)$ for all $W\supset f(V)$ which are open and take a colimit of this diagram of inclusions (all $W$ are bigger, so getting down to the lower bound means going reverse to the direction of inclusions). But inclusion $f(V)\subset W$ implies $V\subset f^{-1}(f(V))\subset f^{-1}(W)$. The latter identity $V\subset f^{-1}(W)$ involves only open sets. Thus we take a colimit over the comma category $(V\downarrow f^{-1})$ of $G$. If $G$ is a sheaf, the colimit $G(V)$ understood as a rule $V\mapsto G(V)$ is still not a sheaf, we need to sheafify. The result is sheaf-theoretic pullback

$$f^{-1}G=\mathrm{sheafify}(V\mapsto {\mathrm{colim}}_{V\hookrightarrow f^{-1}W}G(W))=\mathrm{sheafify}(V\mapsto {\mathrm{colim}}_{(V\downarrow f^{-1})}G)$$f^{-1}G = \mathrm{sheafify}(V\mapsto\mathrm{colim}_{V\hookrightarrow f^{-1}W} G(W)) = \mathrm{sheafify}(V\mapsto\mathrm{colim}_{(V\downarrow f^{-1})} G)

which is a sheaf, and one can analyze this construction to show that $f^{-1}$ is a left adjoint to $f_{*}$. This usage of left Kan extension persists in the more general case of Grothendieck topologies.

Remark on terminology: pushforward vs. pullback

Generally, for $p:C\to C\prime$ a functor, the induced “precomposition” functor on functor categories

$$[C\prime ,D]\stackrel{-\circ p}{\to }[C,D]$$[C', D] \stackrel{- \circ p}{\to} [C,D]

is spoken of as pulling back a functor on $C\prime$ to a functor on $C$, as this operation goes in the direction opposite to that of $p$ itself. For this reason, we have above denoted this functor by $p^{*}$. Likewise, one might call the (left or right) Kan extensions along $p$ a push forward of functors from $C$ to functors on $C\prime$.

This notation also coincides with that for geometric morphisms in one case: any functor $p:C\to C\prime$ between small categories induces a geometric morphism $[C,\mathrm{Set}]\to [C\prime ,\mathrm{Set}]$ of presheaf toposes, whose inverse image is the above $p^{*}$ and whose direct image $p_{*}$ is the right Kan extension functor. Note that $p^{*}$ preserves (finite) limits, as required of an inverse image functor, since it has a left adjoint, namely left Kan extension.

On the other hand, if $p$ is additionally a flat functor, then the above precomposition functor is also the direct image of a geometric morphism, whose inverse image is given by left Kan extension (which preserves finite limits when $p$ is flat). More generally, if $C^{\mathrm{op}}$ and $(C\prime {)}^{\mathrm{op}}$ are sites and $p^{\mathrm{op}}:C^{\mathrm{op}}\to (C\prime {)}^{\mathrm{op}}$ is flat and preserves covering families (i.e. it is a morphism of sites), then precomposition is the direct image of a geometric morphism $\mathrm{Sh}(C^{\mathrm{op}})\to \mathrm{Sh}((C\prime {)}^{\mathrm{op}})$ between sheaf toposes.

For example, $C^{\mathrm{op}}$ and $(C\prime {)}^{\mathrm{op}}$ might be the posets $\mathrm{Open}(X)$ and $\mathrm{Open}(X\prime )$ of open subsets of topological spaces (or locales) $X$ and $X\prime$ and inclusions, in which case

$$\mathrm{Open}(X{)}^{\mathrm{op}}\to \mathrm{Open}(X\prime {)}^{\mathrm{op}}$$Open(X)^{op} \to Open(X')^{op}

come from continuous maps of topological spaces going the other way

$$X\leftarrow X\prime :f,$$X \leftarrow X' : f \,,

via the usual inverse image $f^{-1}:O(X{)}^{\mathrm{op}}\to O(X\prime {)}^{\mathrm{op}}$ of open subsets.

Thus, in such cases, the functor $p^{*}$, which looks like a pullback of functors along $p=f^{-1}$, corresponds geometrically to a push-forward of (pre)sheaves along $f$. Therefore, in presheaf literature (such as Categories and Sheaves) the precomposition functor induced by $p$ is usually denoted $p_{*}$ and not $p^{*}$.

It is however noteworthy that also the opposite perspective does occur in geometrically motivated examples. For instance

• if $C$ is the discrete category on smooth space and $D=U(1)$ is the discrete category on the smooth space $X$ underlying the Lie group $U(1)$, then smooth functors (i.e. functors internal to smooth spaces) $F:C\to D$ can be identified with smooth $U(1)$-valued functions on $X$, and the functor on these functor categories induced by a smooth functor $p:C\to C\prime$ does correspond to the familiar notion of pullback of functions;

• and similar in higher degrees: if $C=P_1(X)$ is the smooth path groupoid of a smooth space and $D=BU(1)$ the smooth group $U(1)$ regarded as a one-object Lie groupoid, then smooth functors $C\to D$ correspond to smooth 1-forms $\in {\Omega }^1(X)$ on $X$, and precomposition with a smooth functor $p:P_1(X)\to P_1(X\prime )$ corresponds to the familiar notion of pullback of 1-forms.

This means that whether or not Kan extension corresponds geometrically to pushforward or to pullback depends on the way (covariant or contravariant) in which the domain categories $C$, $C\prime$ are identified with geometric entities.

Related concepts

• Kan extension, (∞,1)-Kan extension

• base change

  • dependent sum, dependent product

  • dependent sum type, dependent product type

References

Textbook sources include

section 3.7 of

• Francis Borceux, Handbook of Categorical Algebra I

section 2.3 in

• Kashiwara and Shapira, Categories and Sheaves

The book

• Saunders MacLane, Categories for the working mathematician

has a famous treatment of Kan extensions with a statement: “The notion of Kan extensions subsumes all the other fundamental concepts in category theory”. Of course, many other fundamental concepts of category theory can also be regarded as subsuming all the others.

For Kan extensions in the context of enriched category theory see

• Eduardo Dubuc, Kan extensions in enriched category theory, Lecture Notes in Mathematics, Vol. 145 Springer-Verlag, Berlin-New York 1970 xvi+173 pp.

and chapter 4 of

• Max Kelly, Basic Concepts of Enriched Category Theory, Cambridge University Press, Lecture Notes in Mathematics 64, 1982, Republished in: Reprints in Theory and Applications of Categories, No. 10 (2005) pp. 1-136 (pdf)

The (∞,1)-category theory notion is discussed in section 4.3 of

• Jacob Lurie, Higher Topos Theory

For uses of Kan extension in the study of algebras over an algebraic theory see

• Paul-André Melliès and Nicholas Tabareau, Free models of T-algebraic theories computed as Kan extensions (web)

Preservation of certain limits by left Kan extended functors is discussed in

• Francis Borceux, and Brian Day, On product-preserving Kan extension, Bulletin of the Australian Mathematical Society, Vol 17 (1977), 247-255 (pdf)

• Panagis Karazeris, and Grigoris Protsonis, Left Kan extensions preserving finite products (pdf)

The general notion of extensions of 1-morphisms in 2-categories is discussed in

• Steve Lack, A 2-categories companion, in John Baez, Peter May, Towards Higher Categories, Springer, (2009) (arXiv:math/0702535)