nLab Dirac field
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Spin geometry
spin geometry, string geometry, fivebrane geometry …
Ingredients
Spin geometry
rotation groups in low dimensions:
see also
String geometry
Fivebrane geometry
Ninebrane geometry
Contents
Idea
In physics, specifically in field theory, a Dirac field is an electromagentially charged and possibly massive a fermionic spinor field.
This includes fermions in the standard model of particle physics, such as electrons, quarks, neutrinos and muons, after the Higgs mechanism has equipped them with mass.
Mathematically, the Dirac field is the field whose field bundle is a spinor bundle with typical fiber a Dirac representation in odd super-degree and whose equation of motion is a Dirac equation.
Notice that there are other spinor fields which would not be called “Dirac fields”, such as those transforming in a Majorana representation or a Weyl representation, or for example the gravitino field which would be called a Rarita-Schwinger field.
Properties
Free Dirac field in Couloumb background
In solid state physics, the electrons described by the Dirac equation are encountered in the electromagnetic background field that is sourced by atomic nuclei such as those on the lattice sites of a crystal.
In a common approximation used in condensed matter theory for computing ground state-properties of crystals, the nuclei are typically treated as motionless (due to their large mass compared to that of the electrons), hence sourcing a static Coulomb background field, while the electromagnetic interaction of the electrons with each other is neglected. In this approximation one is dealing with a “free Dirac field in a static Coulomb background”.
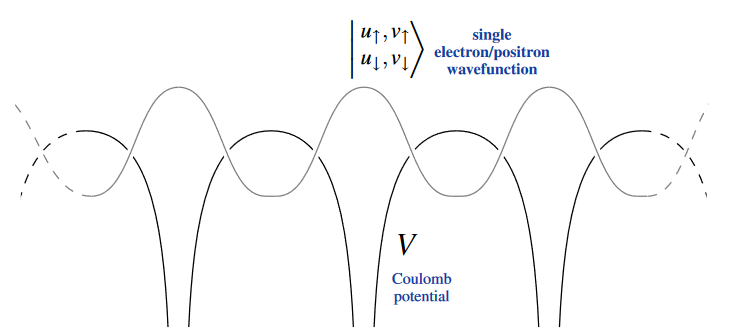
(graphics from SS22, cf. Rößler 2004, Fig. 2.1)
The vacua/ground state of the free Dirac field in such a “classical Coulomb background” (review in Thaller 92, Sec. 10) have been computed in Klaus & Scharf 77 and found to be characterized by Fredholm operators (amplified in Carey, Hurst & O’Brien 82) whose kernel/cokernel are the Hilbert spaces of single electron/positron quantum states which are occupied in the charged vacuum, hence whose Fredholm index is the total charge in this vacuum.

Related concepts
Reference
General
A concise collection of the Dirac field over Minkowski spacetime is in
- Radovan Dermisek, qft I-9, 2009 (pdf, pdf)
with background on spinor fields in
- Radovan Dermisek, qft I-8, 2009 (pdf, pdf)
A textbook account of the interacting Dirac field in the context of causal perturbation theory:
-
Günter Scharf, section 2.2 of Finite Quantum Electrodynamics – The Causal Approach, Berlin: Springer-Verlag, 1995, 2nd edition
-
Günter Scharf, section 1.8 of Quantum Gauge Theories – A True Ghost Story, Wiley 2001
Textbook account of the free Dirac field but possiblyin an electromagnetic background field:
- Bernd Thaller, Section 10 of: The Dirac Equation, Texts and Monographs in Physics, Springer (1992) (doi:10.1007/978-3-662-02753-0)
Free Dirac field in Coulomb background
Discussion of the charged vacua/ground states of the free Dirac field in a strong Coulomb background field (such as that sourced by atomic nuclei on a crystal lattice):
Identification of the vacua/ground states of the free Dirac field in a Coulomb background field:
- Martin Klaus, Günter Scharf, The regular external field problem in quantum electrodynamics, Helv. Phys. Acta 50 (1977) [doi:10.5169/seals-114890, hpa-001:1977:50::1019]
and the observation that these vacua are characterized by Fredholm operators whose index is the total charge in the vacuum:
- Alan Carey, Charles Angas Hurst, Denis O'Brien, Automorphisms of the canonical anticommutation relations and index theory, Journal of Functional Analysis 48 3 (1982) 360-393 [doi:10.1016/0022-1236(82)90092-1]
This curious observation seems not to have been followed up on much, but some related references are listed in Thaller 92, p. 319.
Last revised on September 7, 2023 at 06:59:04. See the history of this page for a list of all contributions to it.