nLab Fukaya category
Context
Symplectic geometry
Background
Basic concepts
Classical mechanics and quantization
-Category theory
Background
Basic concepts
-
equivalences in/of -categories
Universal constructions
Local presentation
Theorems
Extra stuff, structure, properties
Models
Stable Homotopy theory
Ingredients
Contents
Contents
Idea
The Fukaya category (named after Fukaya 1993) of a symplectic manifold is an A-∞ category having Lagrangian submanifolds of as objects.
When two Lagrangian submanifolds and of meet transversally, their hom-space in the Fukaya category is roughly defined as the vector space spanned by the intersection points .
One of the main difficulties in giving a rigorous definition of the Fukaya category in general relies precisely in the problem of correctly defining the hom-spaces for nontransversal intersections. As one could expect, the same difficulty carries on to the definition of the multilinear operations in the Fukaya category: when Lagrangians intersect transversally one has a clear geometric intuition of the multiplication
in terms of counting pseudo-holomorphic disks into whose boundaries lie on the given Lagrangian submanifolds, but when intersections are nontransverse, the definition of becomes more elusive.
When defined, the Fukaya category is an -category which consitutes one side of the duality of homological mirror symmetry.
In string theory
A-Model topological string
In string theory, the Fukaya category of a symplectic manifold represents the category of D-branes in the A-model – the A-branes – with target space . For Landau-Ginzburg models, the category of A-branes is described by Fukaya-Seidel categories.
The assignment that sends a symplectic manifold to its Fukaya category extends to a functor on a variant of the symplectic category with Lagrangian correspondences as morphisms. This is supposed to be the FQFT incarnation of Donaldson theory. See at Lagrangian correspondences and category-valued TFT for more on this and see at homological mirror symmetry.
Yukawa couplings in intersecting D-brane models
In intersecting D-brane models Yukawa couplings are encoded by worldsheet instantons of open strings stretching between the intersecting D-branes (see Marchesano 03, Section 7.5). Mathematically this is encoded by derived hom-spaces in a Fukaya category (see Marchesano 03, Section 7.5).
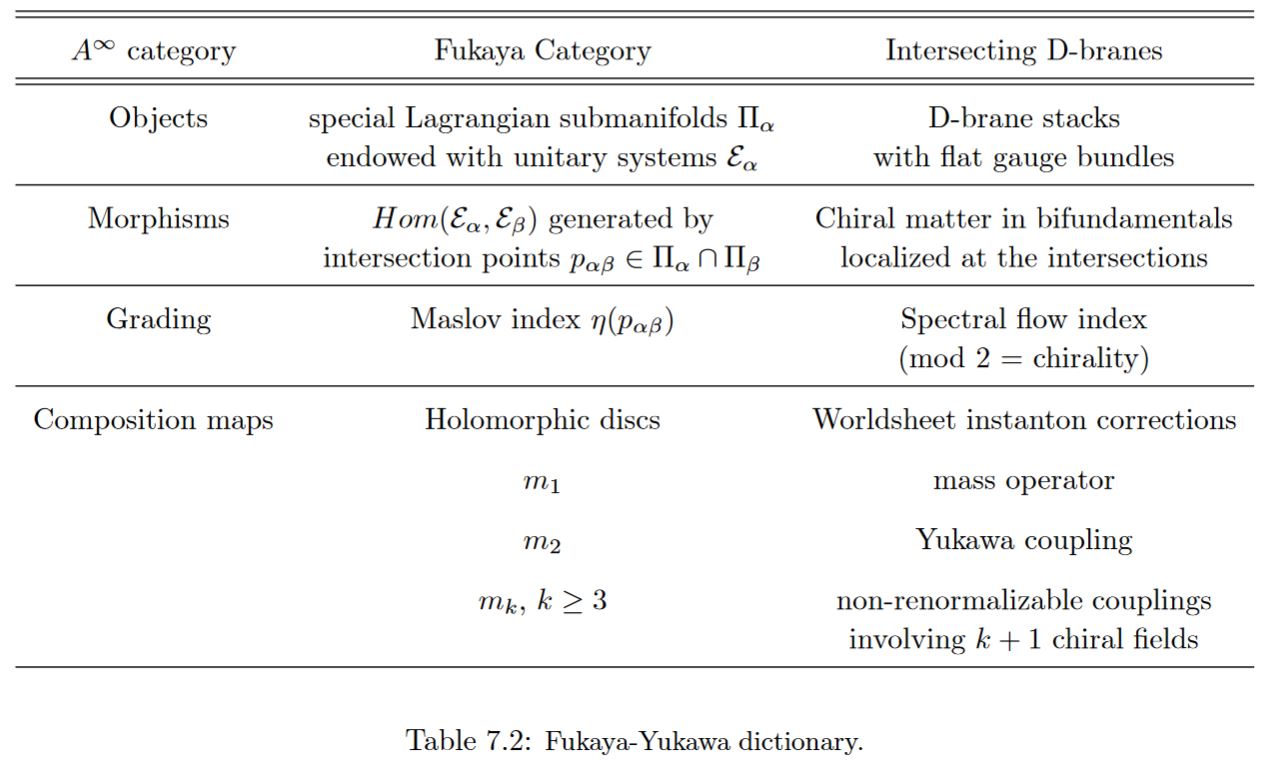
table grabbed from Marchesano 03
Related concepts
References
Fukaya categories are named after:
- Kenji Fukaya, Morse homotopy, -category, and Floer homologies, Proceedings of GARC Workshop on Geometry and Topology ‘93 (Seoul, 1993) [pdf]
Monographs:
-
Kenji Fukaya, Yong-Geun Oh, Hiroshi Ohta, Karo Ono, Lagrangian intersection Floer theory - anomaly and obstruction, Studies in Advanced Mathematocs 46, AMS (2009) [ISBN:978-0-8218-5253-8]
-
Paul Seidel, Fukaya categories and Picard-Lefschetz theory, EMS (2008) [doi:10.4171/063]
Introduction:
- Denis Auroux, A beginner’s introduction to Fukaya categories, lectures at Summer School on Contact and Symplectic Topology, Université de Nantes (June 2011) [arXiv:1301.7056]
and with an eye towards mirror symmetry:
On the relation to Lagrangian cobordism:
- David Nadler, Hiro Tannaka, A stable infinity-category of Lagrangian cobordisms (arXiv:1109.4835)
Relation to Yukawa couplings in intersecting D-brane models:
- Fernando Marchesano, section 7.5 of Intersecting D-brane Models [arXiv:hep-th/0307252]
Towards a higher generalization:
- James Pascaleff, Nicolò Sibilla. Speculations on higher Fukaya categories (2025). (arXiv:2503.20906).
Last revised on March 28, 2025 at 08:49:02. See the history of this page for a list of all contributions to it.