nLab Kleisli category of a comonad
Context
2-Category theory
Definitions
Transfors between 2-categories
Morphisms in 2-categories
Structures in 2-categories
Limits in 2-categories
Structures on 2-categories
Higher algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Contents
Idea
Formally dually to how a monad has a Kleisli category so also a comonad has a Kleisli category: its objects are the objects of , a morphism in the Kleisli category is a morphism
in , and the composition of two such in the Kleisli category is represented by the morphism in given by
Sometimes the term co-Kleisli category is encountered, but this is redundant, since there is only one notion of Kleisli category for a comonad.
Examples
General
Example
For an idempotent comonad the Kleisli category is the coreflective subcategory of its modal types.
Example
In typed functional programming, the Kleisli category of a comonad can be used to model call-by-name? programming languages. Dually, the Kleisli category of a monad may be used to model call-by-value?-programming, see there.
Generally, see at monad (in computer science) for more on this.
Specific
Example
(matrix multiplication as Kleisli composition)
For
-
a field
-
be a finite set
consider the base change adjoint triple of -indexed sets of -vector spaces (-vector bundles over ):
By the assumption that is finite and since Vect has biproducts, the colimit/coproduct
agree (we have an ambidextrous adjunction) and are both equivalent to the direct sum:
Accordingly, the underlying endofunctors of the induced monad and comonad on
agree, to make a self-adjoint functor
which carries the structure both of a monad and of a comonad.
We claim that
-
the categories of
-
co-free -coalgebras
are both equivalent to the category of -vector spaces,
-
where:
-
the Kleisli category of exhibits such linear maps as -tuples of columns of -block matrices;
-
the coKleisli category of exhibits such linear maps as -tuples of rows of -block matrices
-
with (co)Kleisli composition expressing the operation of block-matrix multiplication.
In particular, on the (co)free algebras of the form this statement holds in the sense of actual -matrices with entries in (as opposed to block matrices).
Since every linear map admits some -block matrix representation, the second statement implies the first by the Kleisli theorem (see here).
Moreover, the second statement follows by direct inspection of the Kleisli morphisms (and dually for the coKleisli morphisms):
For this, identify a coKleisli morphism (where our notation now borrows from dependent linear type theory in order to express morphisms between -indexed sets of vector spaces)
with the -tuple of “block ” matrices that it evidently encodes.
Observe that the comultiplication on the -comonad is given by the diagonal map into the biproduct, coming from the “randomness unit” (terminology from modal quantum logic, following CQTS (2022)):
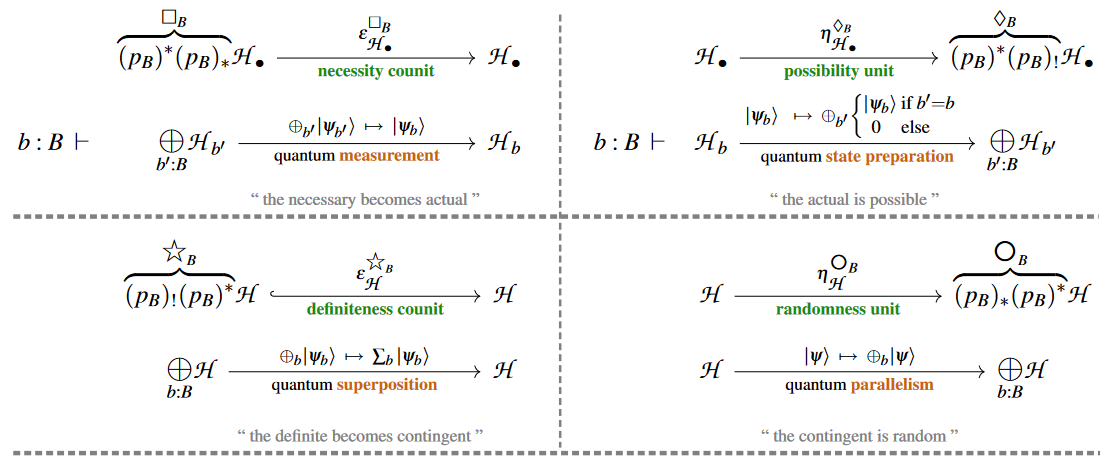
Using this, one readily sees that the Kleisli construction indeed sends such -tuples of block-matrix rows to the linear map which is given by the corresponding full matrix, and that the Kleisli composite with any other
is indeed the row-decomposition of the corresponding matrix product:
The formally dual argument (now using the “definiteness counit”) shows the analogous statement for Kleisli morphisms and column-decomposition of block matrices:
Example
For a jet comonad, then morphisms in its coKleisli category are differential operators (see there).
Related concepts
References
The equivalence of categories between the Kleisli category over a given comonad with the Kleisli category of an adjoint monad (if it exists):
- Mark Kleiner, Adjoint monads and an isomorphism of the Kleisli categories, Journal of Algebra
Volume 133 1 (1990) 79-82 [doi:10.1016/0021-8693(90)90069-Z]
Some introductory material on comonads, coalgebras and co-Kleisli morphisms:
- Paolo Perrone, Notes on Category Theory with examples from basic mathematics, Chapter 5. (arXiv)
Last revised on April 12, 2023 at 11:46:05. See the history of this page for a list of all contributions to it.