nLab necessity and possibility
Context
Modalities, Closure and Reflection
Contents
Idea
In the context of modal logic and specifically in epistemic modal logic, two key modalities that one wants to consider are those of necessity and possibility.
The idea is to consider for any proposition
-
a proposition labeled expressing the idea that “ is necessarily true”;
-
a proposition labeled expressing the idea that “ is possibly true”.
Via S4 modal logic
A common formalization of necessity/possibility is via S4 or S5 modal logic, whose axioms are motivated as follows:
For every comonadic modality like necessity , one typically demands that it preserves implication, in the sense that
This preservation of implication is called the axiom K. In traditional non-categorical modal logic this is often all that is considered (“K modal logic), because the operators are considered de Morgan dual:
In an intuitionistic modal logic, one would also demand that preserves implication in a suitable sense, such as
One may also ask for a further compatibility such as , as Simpson does.
Similarly, the axiom implies that preserves logical conjunction, i.e. . The nullary version follows from the “necessitation rule” which says that if is provable in the empty context, then so is . (This is an additional rule assumed in modal logics.) From duality (1) it follows that preserves logical disjunction (both binary and nullary), while intuitionistically one may want to ask for this separately (Simpson does, but Biermann & de Paiva 2000 don’t).
A minimum further requirement on a formalization of and to have the interpretation of “necessity” and “possibility” is arguably that there are implications
-
;
-
,
expressing that if something is necessarily true, then that should mean that it is true in all instances, and that if something is true in one instance, then it is evidently possible for it to be true. With these additions to the above K modal logic, one speaks of T modal logic.
By similar plausibility arguments one often demands that
which may be read as expressing that iterating the previous reasoning does not yield any new insight. This additional enhancement to T modal logic yields S4 modal logic.
In terms of categorical logic interpreting propositional logic into a Heyting algebra, the S4 axioms just say (Bierman & de Paiva 1996, 2000) that:
-
is a (necessarily idempotent) comonad which is monoidal, hence product-preserving; and
-
is a (necessarily idempotent) monad which is a “-strong functor”, and (perhaps) preserves coproducts.
As usual, we can also replace the Heyting algebra by a cartesian closed category, thereby obtaining a “proof-relevant” system; in this case monoidality of does not imply directly that it preserves products, although one might reasonably ask that it does (see strong monads in computer science). Note that if one moves from Heyting algebras to cartesian closed categories the (co)monads are not necessarily idempotent (and there are good proof-theoretical reasons why they should not be so).
The above reasoning makes plausible that any operators expressing “necessity” and “possibility” should at least satisfy these (co)monad axioms. However, not every (co)monad is sensibly interpreted this way.
For example, there is
-
the (idempotent) comonad which sends every proposition to false (the non-being-modality);
-
the (idempotent) monad which sends every proposition to true (the being-modality).
These satisfy all of the above axioms (as well as more axioms that are being considered, such as those called S5 modal logic) but they are not a very good interpretation of the informal concepts of “possibility” and “necessity”. Under this interpretation nothing is necessarily true, and everything is possibly true. While this is not nonsensical, it is not very interesting and doesn’t correspond well to our intuitive meanings of “necessary” and “possible”.
This issue becomes more pronounced as one generalizes from the small realm of propositional logic to include both or either of:
-
types more general than propositions (in modal type theory);
-
first-order logic with quantifiers, hence hyperdoctrines/dependent types.
There are many modal operators in such contexts which are all modeled by (idempotent) (co)monads but which do not have the interpretation of expressing the modes of “necessity” or “possibility”. See at modal operator for some examples.
Therefore it makes sense to ask which additional axioms on a modal operator make it an accurate formalization of the informal concepts of necessity and possibility. The answer to this may depend on context and intention (after all one is trying to find a precise formulation of an a priori informal idea).
Possible worlds via dependent types
One common philosophical interpretation of “necessarily” and “possibly” is (Kripke semantics) in terms of a collection of “possible worlds” that are similar to the “real world”, but not the same. Under this interpretation, a proposition is necessarily true if it is true in all possible worlds, and possibly true if it is true in some possible world.
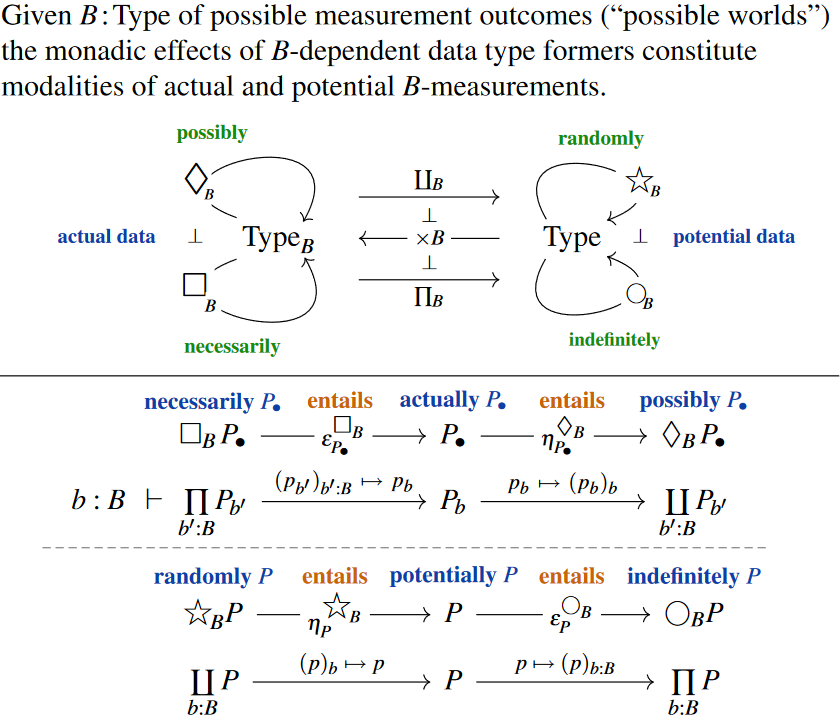
Now the idea of a proposition being true “necessarily in all possible cases” or “possibly at least in one case” is formally very well established in predicate logic: it is just the interpretation of the universal quantifier “for all” and of the existential quantifier “there exists” . In categorical logic, these quantifiers (see there for details) are part of adjoint triple whose middle piece is context extension, and as such they naturally induce a comonad and a monad. Thus, if we interpret “necessarily” and “possibly” according to S5 modal logic in terms of possible worlds, we can model them by this base change adjoint triple (cf. Awodey 2006, p. 279):
Globally
In more detail, let be the context type of variables/terms on which the propositions depend, i.e. the collection “of all possible worlds” (in fact a Kripke frame for S5 modal logic, see there). Any specific choice of may be taken as specifying what is to be understood as a “possible world”.
Writing for the category of all context-free types under consideration and writing for the category of types in context “”, then in categorical logic (for instance might be a hyperdoctrine over a category of contexts containing objects and ) the quantifiers and participate in a base change adjoint triple
In a context of pure logic this would be called
existential quantifier context extension universal quantifier
whereas in a context of dependent type theory this would be called
dependent sum context extension dependent product.
In either case, under the suitable version of propositions as types (and using bracket types etc. if desired), the operations and have the usual interpretation of “for all” and “there exists”.
Note, however, that these operations change the context from to . In other words, if a proposition depends on , so that it may be true in some worlds and false in others, then and no longer depend on . The idea of a necessity and a possibility modality is to send a proposition in some context to a proposition in the same context, so that we can for instance say that and so on. Thus we need to make and into propositions that again depend on — even if they now depend trivially on , being extended back from the absolute context to .
This is just what is accomplished by passing from the above adjoint triple to the induced adjoint pair on by forming composites with the context extension operation
With this, if is a proposition about terms of (a -dependent type) then
-
is true/inhabited precisely if is true/inhabited, hence (that is the standard interpretation of the quantifier) if it is possible for to be true for some ;
-
is true/inhabited precisely if is true/inhabited, hence (that is again the standard interpretation of the quantifier) if necessarily holds for all .
Thus, this gives one syntactic formalization of the informal meaning of “necessity” and “possibility”. The natural semantics for these base change operations is a generalization of the simple traditional possible worlds semantics of propositional necessity and possibility modalities. (There are, however, more complicated possible worlds semantics.)
Moreover, with this formalization, the modal operator is left adjoint to and hence both form an adjoint modality. As discussed there, this is a formalization of opposite concepts, which reflects well the opposition of necessity and possibility in their informal meaning.
Observe how the corresponding unit and counit maps properly reflect the intended logic of necessity, actuality and possibility:

Some technical remarks:
-
In general, and as defined above are, while being a monad and comonad, respectively, not an idempotent monad and idempotent comonad if generalized from first-order hyperdoctrines to more general dependent type theories. But this just reflects the usual issues with propositions as types, see there for more discussion.
-
While base change-adjunctions are essentially unique and not free to choose, there is a genuine choice in the above given by the choice of context . This is reflected in the subscripts of and above. It is the choice of this that gives different kinds of possibility and necessity. More generally there is in fact not just a choice of a context, but of a morphism of contexts, reflecting what is often called “accessibility of possible worlds”. This we come to below.
Relation to Potentiality
There is also an adjoint pair on the other side, , of the base change maps, in which the left adjoint is given by context extension back to followed by , and dually the right adjoint is given by followed by . The former is the coreader comonad, whereas the latter is the reader monad (aka function monad):
If we think of the types in the given context – now called “” – as actual types (3) then the types down in the base context should be thought of as potential types that fail to be actual in that they are missing information about their -dependency (see also at nondeterministic computation, here):
The definiteness-counit witnesses their inhabitation as following from that of a definite type after forgetting which definite world was used to inhabit it.
More in detail, since is a conservative functor, the monadicity theorem (see this example) says
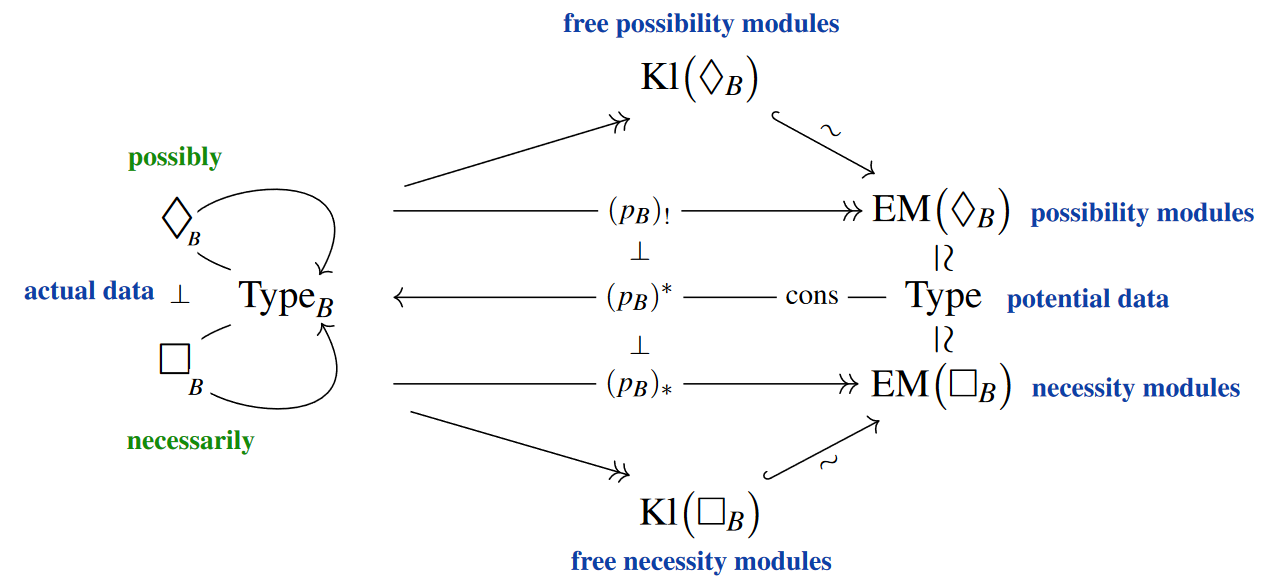
that the types are equivalently
-
those actual types which carry a possibility-monad action
-
those actual types which carry a necessity-co-monad co-action
(The same conclusion in known in the theory of lenses in computer science, see there.)
Hence:

This formalization compares reasonably well with Aristotle‘s discussion, who wrote (in the translation from Ferroni & Gili (2016), §44) first that:
of non-existent things some exist potentially
which is our
and then:
if they exist … it is not possible that it is true to say that: this is possible but will not be the case.
hence (unwinding the double negation)
if potential things exist … and are possible then they will be the case (ie: will be actual)
which is our
Relative version
With this axiomatization via base change, it is immediate to consider the more general relative case where instead of base change to a unit type one considers base change
along any morphism
and sets
If here is an effective epimorphism (a 1-epimorphism) then it exibits an equivalence relation on , where is given by . In traditional possible worlds semantics such equivalence relation in a Kripke frame is called an “accessibility relation between possible worlds” for the case of S5 modal logic. Now
-
is true/inhabited at iff it is true/inhabited at at least one in the same equivalence class of ;
-
is true/inhabited at iff it is true/inhabited at all in the same equivalence classes of .
For more on this see at S5 modal logic – via dependent types.
Examples
Historical examples
Historically, one informal example whose formalization in modal logic has been controversially discussed (see for instance IEP “Rudolf Carnap: Modal Logic”) is the pair of informal assertions
-
“9 is necessarily greater than 7.”
-
“The number of planets in the solar system is 9.”
(Remark. It maybe adds to the joy of modal logic to notice that the second sentence, which was regarded as true in our world at the time the above example was brought up, actually no longer is. Of course this only highlights that indeed this statement is not to be expected to be “necessarily true” in any sense.)
The issue with this example is that if one does not fix a decent formalization of these statements, then naively they seem to imply as correct the statement “The number of planets in the solar system is necessarily greater than 7.”, which however sounds like it ought to be wrong.
We now formalize and then analyze this example with the above prescription.
So let be any type, to be thought of as the type of possible worlds. Write
for the -dependent type that is constant on the ordinary type of natural numbers, i.e. for all .
The terms of , i.e. the natural numbers, canonically extend to -dependent terms of this dependent type
namely to the constant terms, which take the same value (here: 9) for all .
In contrast to this, assume now that is such there is at least one non-constant function . In fact, in the spirit of the informal problem at hand, we require a surjective function. This gives a non-constant term of the constantly -dependent type of natural numbers, which we may just as well call
That is the formalization of the above example we consider, and it should be evident enough. Now we may step back and see what the above formalization produce from this.
So consider the -dependent identity type
By the assumption that is not constant in it follows that the dependent product over of that dependent identity type is the empty type, and so the same is true for applied to it:
- is false.
However, if we assume that there is one for which indeed takes the value 9, then the dependent sum over the dependent identity type contains that coincidence as a term, and so of our dependent identity type is inhabited. Hence
- is true.
In English words, these formal consequences are to be pronounced as:
-
“It is false that it is necessary that the number of planets in the solar system is 9.”
-
“It is true that it is possible that the number of planets in the solar system is 9.”
Which is just as it should be.
Similarly, the -dependent type
is only going to be inhabited if indeed the value is greater than 7 for all . With our formalization assumption above this is not the case, and so one finds that
- is false.
hence
- “It is false that it is necessary that the number of planets in the solar system is greater than 7.”
Quantum modal logic
under construction
We discuss1 the modal logic induced from base change of dependent types, as above, now applied to dependent linear types over finite sets (family of finite types) — to find a natural modal quantum logic (and in fact a natural quantum programming language for quantum circuits, see at quantum circuits via dependent linear types for more on this).
Given a base type (which we take to be finite)
write for the -dependent linear types
The intended categorical semantics is obtained by interpreting as a -indexed set of complex vector spaces (or rather: Hermitian inner product spaces) which the reader may want to think of as being finite dimensional (hence: as Hilbert spaces if positive definite), though this finite-dimensionality condition of is not used in the following (as opposed to the finiteness condition on , which is used).
We assume that our dependent linear type theory realizes base change of linear types along maps of non-linear base types in the form of Wirthmüller-type yoga of six operations:
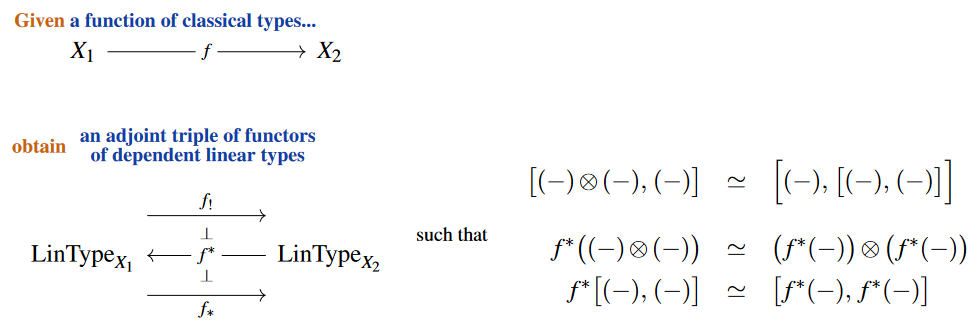
Moreover, we assume that along maps with finite-fibers, such as the terminal map , the left base change agrees with the right base change (“ambidexterity”, so that both give the dependent biproduct over ):
Curiously, in terms of modal logic, this is the Gell-Mann principle of quantum physics, in that it means:
Both these assumptions are verified in the linear homotopy type theory of Riley (2022), §2.4, which should have categorical semantics in (a type-theoretic model category presenting) the -topos of parameterized -module spectra, among which complex vector spaces embed as their Eilenberg-MacLane module spectra .
Recalling from above the quadruple of (co-)monadic modalities associated with any base change one finds that its quantum analog for dependent linear types (along finite fibers (5))
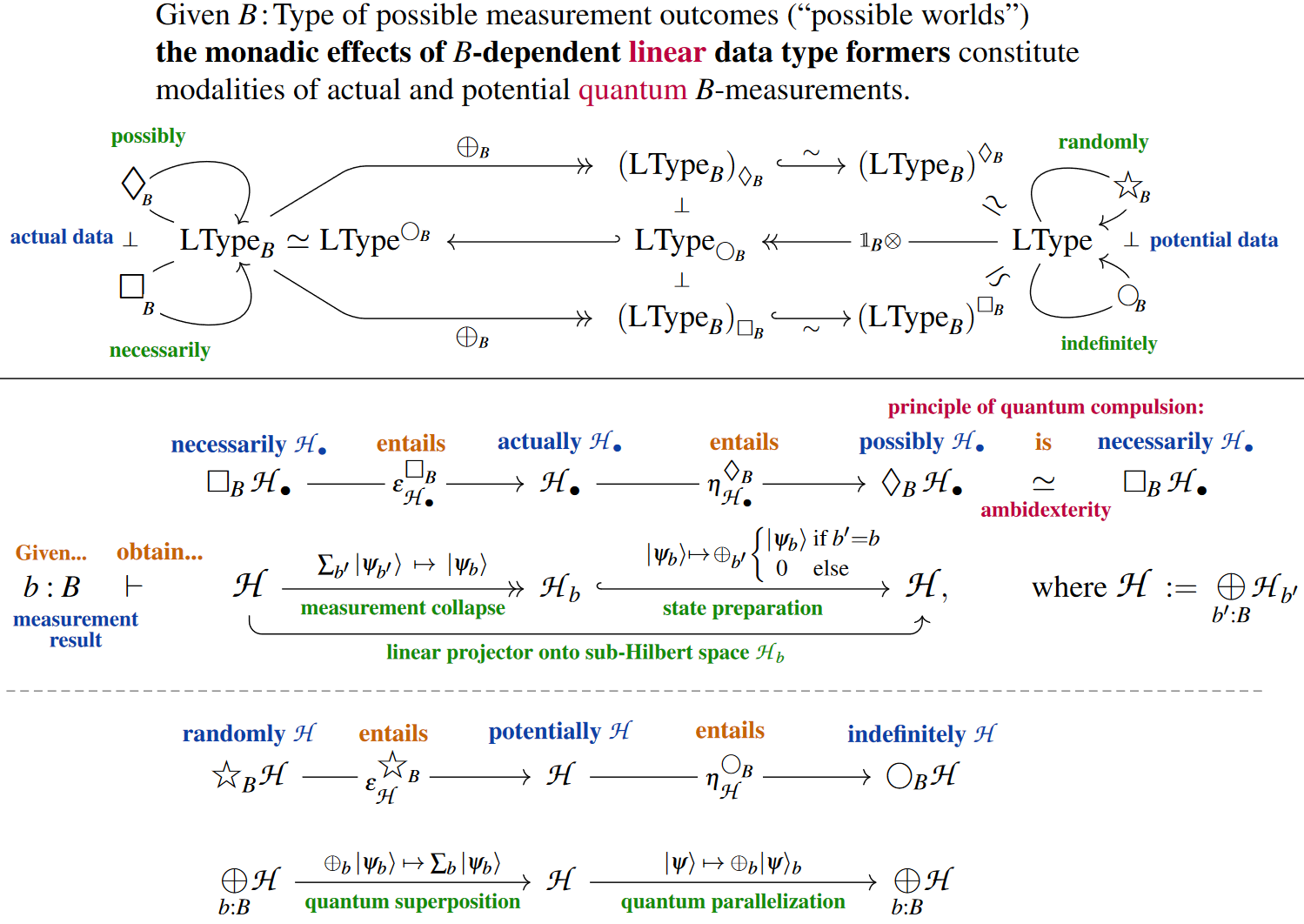
where the interpretation of the modal (co-)units is as follows:
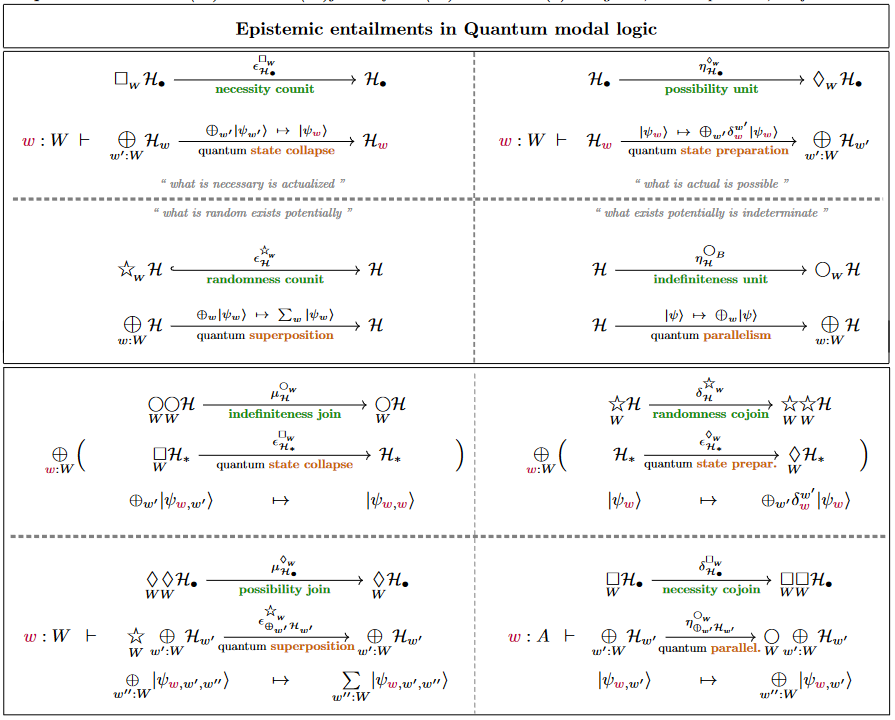
In the context of linear types not just is monadic, but also / (for details see the quantum reader monad), so that the factorization above enhances to the following situation:
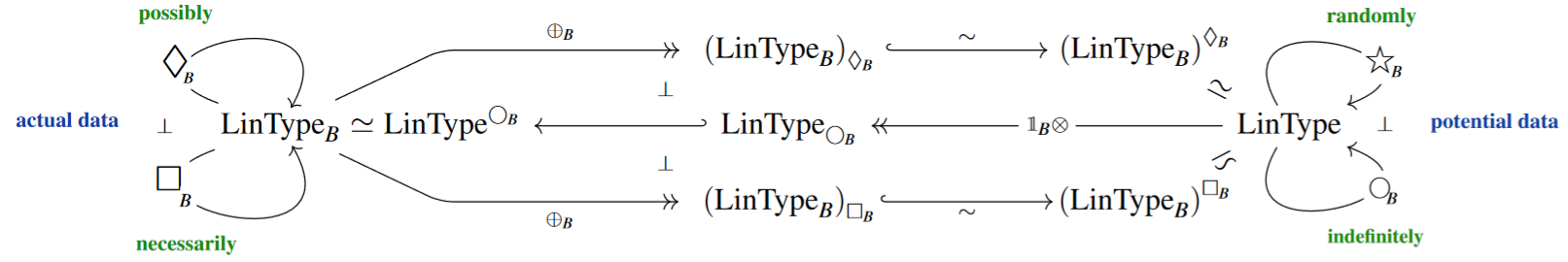
-
abbreviate
-
notationally suppress any outer application of ;
Thereby, the definiteness/randomness modalities in relation to necessity and possibility of classical modal logic (above) may be expressed in quantum modal logic by:
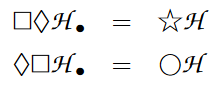
Considering the basic dependent linear type
(which is the tensor unit in ) we may understand
as the Hilbert space which is spanned by a measurement basis .
From all this we find, first of all, that
-
the necessity-counit exhibits the collapse of quantum states under a quantum measurement in the -basis
-
the possibility-unit exhibits the condition quantum state preparation in this basis:

Remark
The collapse-principle of quantum measurement accurately expressed by the above linear necessityactualitypossibility map was maybe first highlighted and made explicit in von Neumann (1932), §III.3, at least for the special case that (in our notation here) (cf. Lüders (1951)).
Remark
We see that the base type (5) of quantum measurement outcomes plays the role of both
(…)
Related concepts
References
Discussion of modal logic of necessity and possibility goes back to Aristotle, as nicely reviewed in
- E. John Lemmon with Dana Scott, pp 1-12 of: An Introduction to Modal Logic – The “Lemmon Notes”, B. Blackwell (1977) [ark:/13960/t3gz25k3h]
In
- Kant, Critique of pure reason 1781
is discussion of modality as one of the categories of pure thought, with sub-categories necessity, possibility and actuality (Wirklichkeit).
In
- Georg Hegel, book 2, section 3, especially book 2, section 3, chapter 2 in Science of Logic (1812)
this is picked up and claimed to be refined to a dialectic system of unities of opposites.
Early discussion in the context of alethic modal logic:
- Georg H. von Wright, An Essay in Modal Logic, North-Holland Publishing (1951)
See also:
-
Saul Kripke, Naming and Necessity (1980)
-
Stanford Encyclopedia of Philosophy, Modal Logic
Making explicit the necessity modal operator as a comonad:
-
Gavin M. Bierman, Valeria de Paiva, Intuitionistic necessity revisited, School of Computer Science research reports-University of Birmingham CSR (1996) [researchgate, pdf]
-
Gavin M. Bierman, Valeria de Paiva, On an Intuitionistic Modal Logic, Studia Logica 65 (2000) 383–416 [doi:10.1023/A:1005291931660, pdf]
-
Satoshi Kobayashi, Monad as modality, Theoretical Computer Science 175 1 (1997) 29-74 [doi:10.1016/S0304-3975(96)00169-7]
-
Natasha Alechina, Michael Mendler, Valeria de Paiva, Eike Ritter: Categorical and Kripke Semantics for Constructive S4 Modal Logic, in Computer Science Logic. CSL 2001 Lecture Notes in Computer Science 2142, Springer (2001) 292 [doi:10.1007/3-540-44802-0_21]
The understanding of Kripke semantics for S5 modal logic as base change is indicated in:
-
Steve Awodey, p. 279 in: Category theory, Oxford University Press (2006, 2010) [doi:10.1093/acprof:oso/9780198568612.001.0001, ISBN:9780199237180, pdf]
-
David Corfield, Chap. 4 of: Modal Homotopy Type Theory: The Prospect of a New Logic for Philosophy (2020)
See also:
-
Jake Chandler, Modality: Necessity and Possibility, lecture notes (pdf)
-
Alex Simpson, The Proof Theory and Semantics of Intuitionistic Modal Logic, Ph.D. Thesis, University of Edinburgh, 1994, web.
-
Internet Encyclopedia of Philosophy, Rudolf Carnap: Modal Logic
-
Following discussion at Topological Quantum Programming in Linear Homotopy Type Theory ↩
Last revised on April 3, 2025 at 11:50:03. See the history of this page for a list of all contributions to it.