nLab monad (in computer science)
This entry is about monads as known from categorical algebra but in their application to computer science. See also at monad (disambiguation).
Context
Computation
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Categorical algebra
internalization and categorical algebra
-
algebra object (associative, Lie, …)
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Contents
- Idea
- Basic idea: Monadic effects
- Refined idea: Strong monads
- Further idea: Monad modules
- Dual idea: Comonadic contexts
- Syntactic idea: Do-notation
- Examples
- Definable monads
- State monad and Random access memory
- Maybe monad and Controlled failure
- Exception monad and Exception handling
- Continuation monad and Continuation-passing
- Axiomatic monads
- Related concepts
- References
Idea
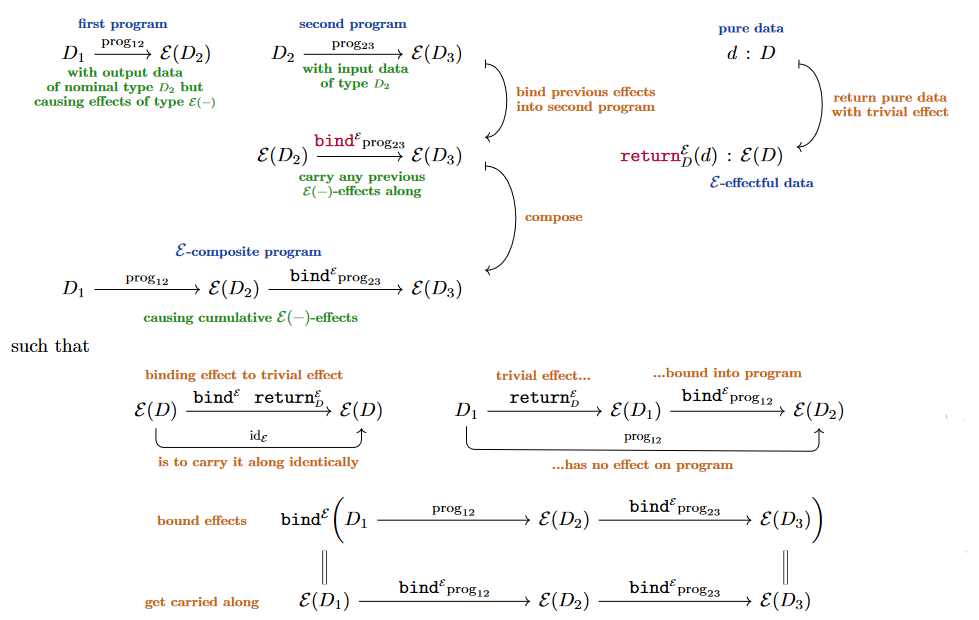
In computer science, a (co-)monad (or (co-)Kleisli triple, or (co-)extension system) is a kind of data type-structure which describes “notions of computations” [Moggi (1989), Moggi (1991)] that may “have external effects or be subject to external contexts/causes” — such as involving random access memory, input/output, exception handling, writing to or reading from global variables, etc. — as familiar from imperative programming but cast as “pure functions” with deterministic and verifiable behaviour, in the style of functional programming.
In short, a (“extension system-style” [Manes (1976), Ex. 3.12] or “Kleisli triple-style” [Moggi (1991), Def. 1.2]) monad in a given programming language consists of assignments (but see below):
-
to any data type of a new data type of “-data with -effects”,
-
to any pair of -effectful functions (programs) of the form and of an effective-composite function (their binding or Kleisli composition),
-
to any data type of a function assigning “trivial -effects”,
such that the binding is associative and also unital with respect to the return operation, hence such that data types with -effectful programs between them constitute a category (the Kleisli category of the given effect/monad ).
We now explain in more detail what this means and what it is good for.
Basic idea: Monadic effects
In programming it frequently happens that a program with “nominal” output data type de facto outputs data of some modified type which accounts for “external effects” caused by the program, where
is some general operation sending data types to new data types .
For example, if alongside the computation of its nominal output data a program also writes a log message String, then its actual output data is the pair of product type .
Or, dually, if the program may fail and instead “throw an exception message” String, then its actual output data is either or , hence is of coproduct type .
Given such an -effectful program and given a subsequent program accepting nominal input data of type and itself possibly involved in further effects of type , then the naïve composition of the two programs makes no sense (unless is actually the trivial sort of effect), but their evident intended composition is, clearly, obtained by:
-
first adjusting via a given prescription
(2)such that :
-
does accept data of type and
-
“acts as while carrying any previous -effects along” (this intuition becomes a formal fact below in (9));
-
-
then forming the naive composition
as follows:
(Beware that we are denoting by “” what in programming languages like Haskell is denoted by “
(-) >>= prog” aka “fish notation”, eg. Milewski 2019 p. 321, and which some authors denote by an upper-star, “”, e.g. Moggi (1991); Uustalu (2021), lecture 1, p. 12.)
Depending on the intended behaviour of these programs, it remains to specify how exactly “carries -effects along”, hence what the “bind” operation (2) does concretely.
For instance, in the above example of a logging-effect, where , the evident way is to use the concatenation and set:
In the other example above, where the effect is the possible throwing of an exception message, the evident way to carry this kind of effect along is to use the codiagonal , which amounts to keep forwarding the exception that has already been thrown, if any:
Whatever design choice one makes for how to “carry along effects”, it must be consistent in that applying the method to a triple of -effectful programs which are nominally composable, then their effectful composition should be unambiguously defined in that it is associative, satisfying the following equation – here called the the first “monad law”:
Finally, for such a notion of effectful programs to be usefully connected to “pure” programs without effects, it ought to be the case that for any program that happens to have no -effects, we have a prescription for how to regard it as an -effectful program in a trivial way. For that purpose there should be defined an operation
which does nothing but “return” data of type , but re-regarded as effectful -data in a trivial way; so that we may construct the trivially effectful program .
For instance, in the above example of log-message effects this would be the operation which assigns the empty string .
In the other example above, of exception handling, the trivial effect is just not to throw an exception, which is just (the right coprojection into the coproduct).
The final consistency condition (i.e. the remaining “monad law”) then is that “carrying along trivial effects is indeed the trivial operation”, i.e. that
Notice that the associativity condition (3) and the unitality condition (5) are jointly equivalent to saying that data types with hom-sets of -effectful programs between them, in the above sense, form a category. In category theory this is known as the Kleisli category of a monad on the category of data types with programs between them:
Traditionally in category theory, the axioms on monads are presented in a somewhat different way, invoking a monad “product” natural transformation instead of the “binding” operation. One readily checks that these two axiomatic presentations of monads are in fact equal – see (7) below –, but the above “Kleisli triple/extension system”-presentation is typically more relevant in the practice of functional programming.
In summary, a choice of assignments (but see below) to data types of
-
,
namely of types of -effectful data of nominal type (1);
-
,
namely of how to execute a prog while carrying along any previous effects (2);
-
,
namely of how to regard plain -data as trivially effectful (4)
subject to:
-
the associativity condition (3)
is called a monad in computer science (also: “Kleisli triple” in functional programming) and serves to encode the notion that all programs may be subject to certain external effects of a kind that is specified by the above choices of monad operations.
Here, for the time being (but see below), we write for the set of programs/functions taking data of type to data of (the hom set in the plain category of types).
The first running example above is known as the writer monad, since it encodes the situation where programs may have the additional effect of writing a message string into a given buffer.
The other running example above is naturally called the exception monad.
Relation to other familiar axioms for monads. The above Kleisli/extension-structure, making a Kleisli-style monad in computer science, may and often is encoded in different equivalent ways:
Alternatively postulating operations
-
(as before)
such that
-
is functorial on data types,
-
is associative and unital (with respect to ) as a natural transformation,
yields the definition of monad more traditionally used in category theory (namely as a monoid object in endofunctors, here on the plain category of data types).
Direct inspection shows that one may bijectively transmute such - and -operators into each other by expressing them as the following composites (using category theory-notation, for instance “ev” denotes the evaluation map):
Refined idea: Strong monads
But in fact, in functional programming-languages one typically considers an enhanced version of the above situation:
In these higher-order languages one has, besides the (hom-)set of programs/functions also the actual data type of functions, namely the function type , which in terms of categorical semantics is the internal hom-object in the cartesian closed category of data types. Therefore, in such languages (like Haskell) the type of the binding operation for given data types , is actually taken to be the function type/internal hom
(where we used the hom-isomorphism of the productinternal hom-adjunction to re-identify the types on the right)
which (beware) is traditionally written without many of the parenthesis, as follows:
In general (except in the base topos of Sets), such an iterated function type/internal hom is richer than (certainly different from) the corresponding plain hom set, and accordingly a “Kleisli triple” defined as above but with the binding operation typed in this internal way is richer or stronger structure than that of a plain monad on the underlying category of types: namely it is an enriched monad or equivalently a strong monad with respect to the self-enrichment of the symmetric monoidal closed category of types (Moggi 1991 §3, cf. Goubault-Larrecq, Lasota & Nowak 2002, McDermott & Uustalu (2022)).
On such an enriched/strong monad, the bind operation is defined as the following composite:
In particular, monads as used in functional programming languages like Haskell are really strong/enriched monads, in this way.
In this case – and in most discussions by default – the symmetric monoidal closed category of types is assumed to be cartesian closed (“classical types”) but in contexts of linear type theory (such as quantum computation) it may be non-cartesian (or both: cf. doubly closed monoidal category).
Yet more structure on effect-monads is available in dependent type theories with type universes, where one may demand that the monad operation is not just an endofunction on the set of types, but an endomorphism of the type universe. At least for idempotent monads this case is further discussed at reflective subuniverse and modal type theory and maybe elsewhere.
Further idea: Monad modules
Further in the practice of programming: if programs may cause external effects, as above, then one will often want to have some of them handle these effects.
This is particularly evident in the above running examples of exceptions whose whole design purpose typically is to be handled when they arise.
Since a “handling” of -effects should mean that these be done with and turned into pure data of some actual type , an -effect handler on(to) a data type should primarily consist of a program of the form
that handles effects produced by -effectful programs , turning them into pure computations .
But in addition, such a handler needs to handle effects that have been “carried along” (2) from previous computations, even along otherwise in-effectful computations ; therefore all these need to be assigned handlers:
Of such choice of effect handling, consistency demands that:
-
first handling all previous effects carried along (2) and then the newly produced effects by a given has the same result as letting take care of carrying along previous effects by passing to and then handling the resulting accumulation at once:
-
handling the trivial effect ought to be no extra operation:
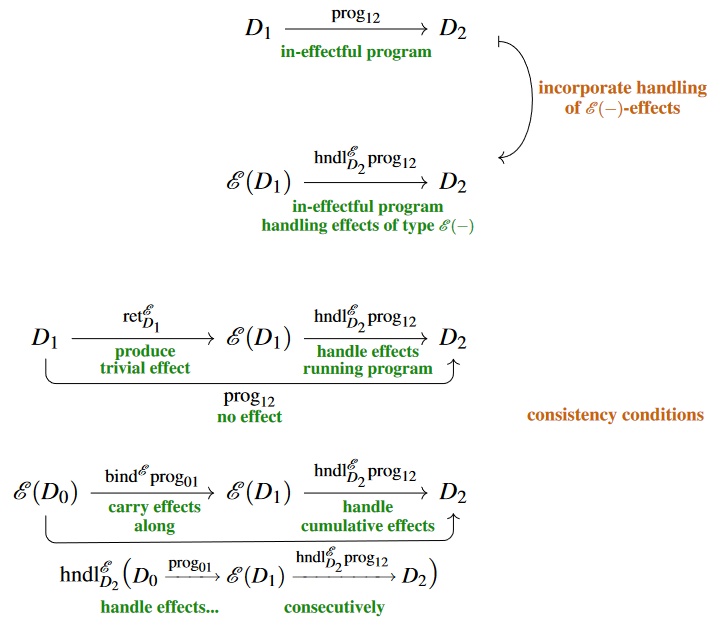
A data structure consisting of such assignments subject to these “laws” is known as an Kleisli triple algebra (e.g. Uustalu (2021), Lec. 2) or algebra over an extension system (see here) for and is bijectively the same as what in traditional category theory is known as an algebra over or -algebra or, maybe best: an -module or -modal type.
Given a pair of such -modal types , , a function is a homomorphism between them if the result of handling -effects before or after applying is the same, hence if for all functions the following diagram commutes:

Free -effect handlers. Notice that above we motivated already the binding operation (2) as a kind of -effect handling: namely as the “carrying along” of previous -effects. This intuition now becomes a precise statement:
For any we may tautologically handle (8) -effects by absorbing them into the data type , with the effect-handler simply being the effect-binding operation (2):
The -effect-handlers (8) arising this way are called free.
The full subcategory of free -effect handlers among all -modal types is known as the Kleisli category. By the Kleisli equivalence, this is equivalent to the (plain) category (6) of -effectful programs that we started with. Here this means that:
- Plain data types with -effectful programs betweem them are equivalently data types freely equipped with the structure of -effect handlers.
which makes a lot of sense.
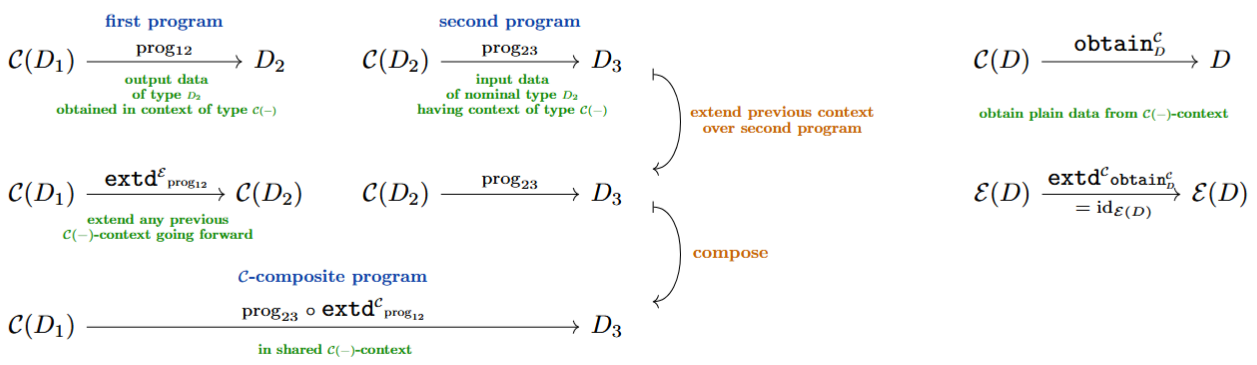
Dual idea: Comonadic contexts

By formal duality, all of the above discussion has a dual version, where now (e.g. Uustalu & Vene (2008), POM13, GKOBU16, KRU20):
-
comonads encode computational contexts (co-effects),
-
their coproduct operation is the duplication (co-join) of contexts which serves to extend (co-bind) contexts over consecutive programs,
-
comodules over comonads are data structures that provide (co-handle) such context.
In more detail:
-
Above we had that:
-
A Kleisli map for a monad is a program
causing an external -effect.
-
A Kleisli-module for a monad is a prescription
for handling such -effects.
-
-
Now dually:
-
A co-Kleisli map for a comonad is a program
subject to an external -“context” (Uustalu & Vene (2008), POM13)
(a -cause).
-
A co-Kleisli co-module for a comonad is a program
producing or providing such -contexts.
(cf. [Uustalu (2021), Lect. 3, slide 9])
-
Syntactic idea: Do-notation
Finally, to turn all this into an efficient programming language one just has to declare a convenient syntax for denoting Kleisli composition.
One such syntax is known as “do notation” (introduced with “{...}” instead of “do” by Launchbury 1993 §3.3, then promoted by Mark Jones in the 1990s [HHPW07, p. 25] and adopted by Haskell in version 1.3, for review see Benton, Hughes & Moggi 2002 p. 70, Milewski 2019 §20.3), which aims to jointly express:
-
successive Kleisli composition in words like “do this, do that, and return the result”,
-
any intermediate bind-operation as “extracting” a -datum out of an -datum with notation
d <- E
Syntactically, do-notation is the following syntactic sugar for combined Kleisli composition and variable binding:
-
do progprog -
do prog1 prog2prog1 bind (\_ -> prog2) -
do (x <- prog1) prog2prog1 bind (\x -> prog2)
This is, first of all, a suggestive notation (in fact a “domain specific embedded programming language”, see there) for expressing effect-binding:
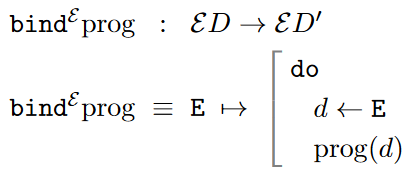
but thereby it furthermore provides a convenient means of expressing successive Kleisli-composition simply by successivley “calling” the separate procedures, much in the style of imperative programming (which thereby is emulated/encapsulated by pure functional programming):

but the notation becomes more suggestive with the rule that the “<-”-symbols may notationally be suppressed for functions with trivial in- or out-put (ie. of unit type ) besides their -effect, as in this example:

This case brings out clearly how the ambient “do…return”-syntax block expresses the (Kleisli-)composition of any number of -effectful procedures.
On top of that the “<-”-syntax is meant to be suggestive of reading out a value. This is accurate imagery for the state monad (and its abstraction to the IO-monad), where from the two pasic operations of reading/writng a global variable
any -stateful program, such as the simple example
may be constucted in do-notation, such as:

For a similar effect monad such as the list monad the analogous do-code for incrementing all entries in a list of numbers looks as follows:

Here The do-notation on the right evokes the idea that in each step a number is “read out” from MyList and then its increment returned — but leaves linguistically implicit the idea that this operation is to be performed for all elements of the list and all results re-compiled into an output list.
Indeed, in general it is misleading to think of Kleisli composition as being about “reading out” data. What Kleisli composition is really about is acting on data that has generators and defining a program by what it does on generators, hence for a given generating datum:
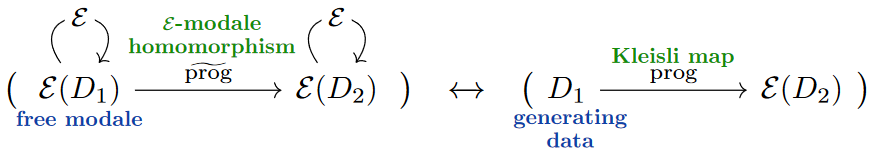
Therefore the conceptually more accurate (if maybe less concise) program-linguistic reflection of the monadic effect-binding operation would be a “for…do”-block:
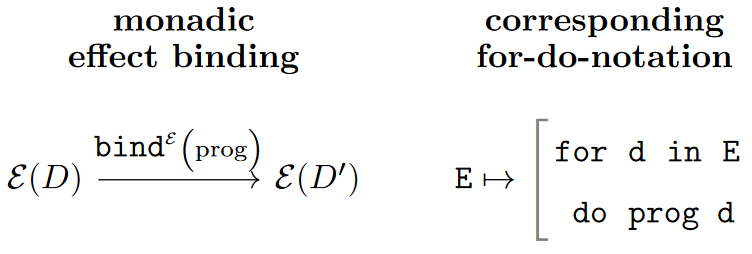
In terms of such for-do-notation, the generic case that we started with above has the following syntactic rendering:

This syntax may be notationally less concise but it evokes rather closely what is actually going on in programming with monadic effects.
For example, the above operation of icrementing all numbers in a given list reads in for…do-notation as follows:

neatly indicative of how the operation is applied for every number found in the list.
(NB.: There is no clash with for…do-notation as used for loops in imperative programming, since functionally these are instead expressed by recursion.)
The appropriateness of rendering effect binding as a for…do-expression becomes yet more pronounced in contexts of substructural typing contexts such as in linear type theory, where the idea of “reading out” of monadic types via “<-”-notation becomes yet more dubious.
For example, consider the relative monad (this example) which sends sets to the vector spaces that are their linear spans:
with
In this case the traditional do-notation would suggest that given a vector one may “read out” a basis element from it – which does not make conceptual sense.
Instead, what’s really happening is that to define a linear map on a vector space equipped with a linear basis (literally: a set of free generators) it is sufficient to define this map for each basis-vector — and this is just what the for…do-notation for the -monad expresses:
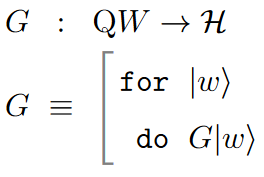
Examples
Definable monads
Various monads are definable in terms of standard type-forming operations (such as product types, function types, etc.). These include the following (cf. Moggi 1991, Exp. 1.1):
-
The maybe monad encodes possible controlled failure of a program to execute.
-
An exception monad, more generally, encodes possible controlled failure together with the output of an error “message” in the general form of data of some type.
-
The reader monad and coreader comonad both encode reading out a global parameter.
-
The writer monad and cowriter comonad both encode writing consecutively into a global resource, such as for a stream.
-
The state monad encodes the possibility of consecutive reading and re-setting a global parameter – this provides a notion of random access memory.
-
The costate comonad encodes a way (a “lens”) to read and write fields in databases.
-
The continuation monad encodes continuation-passing style of program execution.
-
The selection monad encodes selecting a value of a type depending on the values of some function on it.
State monad and Random access memory
A functional program with input of type , output of type and mutable state is a function (morphism) of type – also called a Mealy machine (see there).
Under the (Cartesian product internal hom)-adjunction (currying) this is equivalently given by its adjunct, which is a function of type . Here the operation is the monad induced by the above adjunction and this latter function is naturally regarded as a morphism in the Kleisli category of this monad. This monad is called the state monad for mutable states of type :

Maybe monad and Controlled failure
The maybe monad is the operation . The idea here is that a function in its Kleisli category is in the original category a function of the form so either returns indeed a value in or else returns the unique element of the unit type/terminal object . This is then naturally interpreted as “no value returned”, hence as indicating a “failure in computation”.
Exception monad and Exception handling
(…) exception monad (…)
Continuation monad and Continuation-passing
The continuation monad on a given type acts by .
(…)
Axiomatic monads
Other monads may be supplied “axiomatically” by the programming language, meaning that they are data structures typed as monads, but whose actual type formation, binding- and return-operations are special purpose operations provided by the programming environment.
This includes:
-
the completion monad, as in constructive analysis, used for dealing for instance with real numbers.
In this vein:
- Equipping homotopy type theory (say implemented as a programming language concretely in Coq or Agda) with two axiomatic idempotent monads, denoted and , with some additional data and relations, turns it into cohesive homotopy type theory. See also at Agda flat and at modal type theory.
Related concepts
-
relation between type theory and category theory, categorical semantics, categorical logic
-
Examples of (co)monads in (homotopy) type theory involve in particular modal operators as they appear in
See also:
-
For an approach to composing monads, see
-
Another approach to modelling side effects in functional programming languages are
-
Free monads in computer science appear in the concepts of
-
Other generalizations are:
-
There is also: monad (in linguistics)
References
General
The extension system-style presentation of monads as used in computer science is briefly mentioned in:
- Ernest G. Manes, Sec 3, Ex. 12 (p. 32) of: Algebraic Theories, Springer (1976) [doi:10.1007/978-1-4612-9860-1]
and expanded on in
- Francisco Marmolejo, Richard J. Wood, Monads as extension systems – no iteration is necessary, TAC 24 4 (2010) 84-113 [tac:24-04]
but not related there to computation.
The original observation of monads as “notions of computation” is:
-
Eugenio Moggi, Computational lambda-calculus and monads, in: Proceedings of the Fourth Annual Symposium on Logic in Computer Science (1989) 14-23 [doi:10.1109/LICS.1989.39155]
-
Eugenio Moggi, An abstract View of Programming Languages, LFCS report ECS-LFCS-90-113 (1989) [web, pdf]
(considers also transformations of monads in Def. 4.0.8)
-
Philip Wadler, Comprehending Monads, in Conference on Lisp and functional programming, ACM Press (1990) [pdf, doi:10.1145/91556.91592]
-
Eugenio Moggi, Notions of computation and monads, Information and Computation, 93 1 (1991) [doi:10.1016/0890-5401(91)90052-4, pdf]
-
Philip Wadler, The essence of functional programming, POPL ‘92: Principles of programming languages (1992) 1-14 [doi:10.1145/143165.143169, pdf]
Further discussion:
- Gordon Plotkin, John Power, Notions of Computation Determine Monads, in: Foundations of Software Science and Computation Structures FoSSaCS 2002, Lecture Notes in Computer Science 2303, Springer (2002) [doi:10.1007/3-540-45931-6_24, era:1842/196]
On the impact of Moggi (1991):
- Martin Hyland, John Power, §6 of: The Category Theoretic Understanding of Universal Algebra: Lawvere Theories and Monads, Electronic Notes in Theor. Comp. Sci. 172 (2007) 437-458 [doi:10.1016/j.entcs.2007.02.019, preprint]
Origin of the do-notation for Kleisli composition of effectful programs:
- John Launchbury, §3.3 in: Lazy imperative programming, Proceedings of ACM Sigplan Workshop on State in Programming Languages, Copenhagen (1993) [pdf, pdf]
Introducing the notion of monad transformers:
-
David A. Espinosa, §3.2 in: Building Interpreters by Transforming Stratified Monads (1994) [pdf, pdf]
-
David A. Espinosa, §2.6 in: Semantic Lego, PhD thesis, Columbia University (1995) [pdf, pdf, slides:pdf, pdf]
-
Sheng Liang, Paul Hudak, Mark Jones, Monad transformers and modular interpreters, POPL ‘95 (1995) 333–343 [doi:10.1145/199448.199528]
More (early) literature is listed here:
In the generality of relative monads:
- Thorsten Altenkirch, James Chapman, Tarmo Uustalu, Section 2 of: Monads need not be endofunctors, Logical Methods in Computer Science 11 1:3 (2015) 1–40 [arXiv:1412.7148, pdf, doi:10.2168/LMCS-11(1:3)2015]
The dual notion of comonads in computer science as modelling contexts:
-
Tarmo Uustalu, Varmo Vene, Comonadic Notions of Computation, Electronic Notes in Theoretical Computer Science 203 5 (2008) 263-284 [doi:10.1016/j.entcs.2008.05.029]
-
Tomas Petricek, Dominic Orchard, Alan Mycroft, Coeffects: Unified Static Analysis of Context-Dependence, in: Automata, Languages, and Programming. ICALP 2013, Lecture Notes in Computer Science 7966 Springer (2013) [doi:10.1007/978-3-642-39212-2_35]
-
David Overton, Comonads in Haskell (2014) [web, pdf]
(in Haskell)
on codo-notation for comonadic contexts:
- Dominic Orchard, Alan Mycroft, A Notation for Comonads, in: Implementation and Application of Functional Languages. IFL 2012, Lecture Notes in Computer Science 8241 [doi:10.1007/978-3-642-41582-1_1]
and emphasis on the combination of monads, comonads and graded modalities:
-
Marco Gaboardi, Shin-ya Katsumata, Dominic Orchard, Flavien Breuvart, Tarmo Uustalu, Combining effects and coeffects via grading, ICFP 2016: Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming (2016) 476–489 [doi:10.1145/2951913.2951939, talk abstract, video rec]
-
Shin-ya Katsumata, Exequiel Rivas, Tarmo Uustalu, LICS (2020) 604-618 Interaction laws of monads and comonads [arXiv:1912.13477, doi:10.1145/3373718.3394808]
The identification of (co)effect handling with (co)modales over the given (co)monad:
-
Gordon D. Plotkin, Matija Pretnar, Handling Algebraic Effects, Logical Methods in Computer Science, 9 4 (2013) lmcs:705 [arXiv:1312.1399, doi:10.2168/LMCS-9(4:23)2013]
-
Ohad Kammar, Sam Lindley, Nicolas Oury, Handlers in action, ACM SIGPLAN Notices 48 9 (2013) 145–158 [doi:10.1145/2544174.2500590]
Discussion in actual programming languages such as Haskell:
-
Nick Benton, John Hughes, Eugenio Moggi, Monads and Effects, in: Applied Semantics, Lecture Notes in Computer Science 2395, Springer (2002) 42-122 [doi:10.1007/3-540-45699-6_2]
-
Bartosz Milewski (compiled by Igal Tabachnik), “Monads: Programmer’s Definition”, §20 in: Category Theory for Programmers, Blurb (2019) [pdf, github, webpage, ISBN:9780464243878]
-
Bartosz Milewski, §14 in: The Dao of Functional Programming (2023) [pdf, github]
and Scala:
- Sergei Winitzki, Section 10 of: The Science of Functional Programming – A tutorial, with examples in Scala (2022) [leanpub:sofp, github:sofp]
Further discussion/exposition of the notion and application of (co)monads in computer science:
-
Stephen Brookes, Shai Geva, Computational Comonads and Intensional Semantics, CMU-CS-91-190 (1991) [pdf]
-
Philip Wadler, Monads for functional programming, in M. Broy (eds.) Program Design Calculi NATO ASI Series, 118 Springer (1992) [doi;10.1007/978-3-662-02880-3_8, pdf]
-
Philip S. Mulry: Monads in semantics, Electronic Notes in Theoretical Computer Science 14 (1998) 275-286 [doi:10.1016/S1571-0661(05)80241-5]
-
Stephen Brookes, Kathryn Van Stone, Monads and Comonads in Intensional Semantics (1993) [dtic:ADA266522, pdf, pdf]
(with distributive law of comonad over monad)
-
John Hughes, section 2 of: Generalising Monads to Arrows, Science of Computer Programming (Elsevier) 37 (1-3): 67–111. (2000) (pdf)
-
Robert Harper, Of course ML Has Monads! (2011) (web)
-
Nick Benton, Categorical Monads and Computer Programming, in: Impact150: stories of the impact of mathematics. London Mathematical Society (2015) [pdf, pdf, doi:10.1112/i150lms/t.0002]
-
Emily Riehl, A categorical view of computational effects, talk at CmpseConference (2017) [pdf, pdf]
-
Rob Norris, Functional Programming with Effects, talk at Scala Days 2018 [video: YT]
-
Tarmo Uustalu, lecture notes for MGS 2021 (2021):
Monads and Interaction Lecture 1 [pdf, pdf]
Monads and Interaction Lecture 2 [pdf, pdf]
-
Christina Kohl, Christina Schwaiger, Monads in Computer Science (2021) [pdf, pdf]
See also:
-
Wikipedia, Monad (functional programming)
-
Wikipedia, Side_effect_(computer_science)
The specification of monads in Haskell is at:
and an exposition of category theory and monads in terms of Haskell is in
- WikiBooks, Haskell/Category
Further on the issue of the CS-style monads really being strong monads:
-
Jean Goubault-Larrecq, Slawomir Lasota, David Nowak, Logical Relations for Monadic Types, Mathematical Structures in Computer Science, 18 6 (2008) 1169-1217 [arXiv:cs/0511006, doi:10.1017/S0960129508007172]
-
Dylan McDermott, Tarmo Uustalu, What Makes a Strong Monad?, EPTCS 360 (2022) 113-133 [arXiv:2207.00851, doi:10.4204/EPTCS.360.6]
A comparison of monads with applicative functors (also known as idioms) and with arrows (in computer science) is in
- Exequiel Rivas, Relating Idioms, Arrows and Monads from Monoidal Adjunctions, (arXiv:1807.04084)
In quantum computation
Discussion of aspects of quantum computing in terms of monads:
-
J. K. Vizzotto, Thorsten Altenkirch, A. Sabry, Structuring quantum effects: superoperators as arrows, Mathematical Structures in Computer Science 16 3 (2006) 453-468 [arXiv:quant-ph/0501151, doi:10.1017/S0960129506005287]
The quantum IO monad:
- Thorsten Altenkirch, Alexander Green, The quantum IO monad, Ch. 5 of: Simon Gay, Ian Mackie (eds.): Semantic Techniques in Quantum Computation (2010) 173-205 [pdf, talk slides, doi:10.1017/CBO9781139193313.006]
Exposition:
- Alexander Green, The Quantum IO Monad, Nottingham (2007) [pdf, pdf ]
Implementation in Haskell:
Much of the text and the diagrams in the entry above follow
Last revised on December 27, 2024 at 21:34:58. See the history of this page for a list of all contributions to it.