nLab quantum circuits via dependent linear types

under construction

Introduction

We follow SS23-QM.

The problem

In the context of quantum computation, a pure quantum circuit diagram (originally: “quantum computational network”, Deutsch 1989) is a kind of string diagram (Abramsky & Coecke 2004) in finite-dimensional Hilbert spaces, typically used to express a sequence of low-level quantum gates mapping between spaces of pure quantum states.

A generic pure quantum circuit might look as follows:

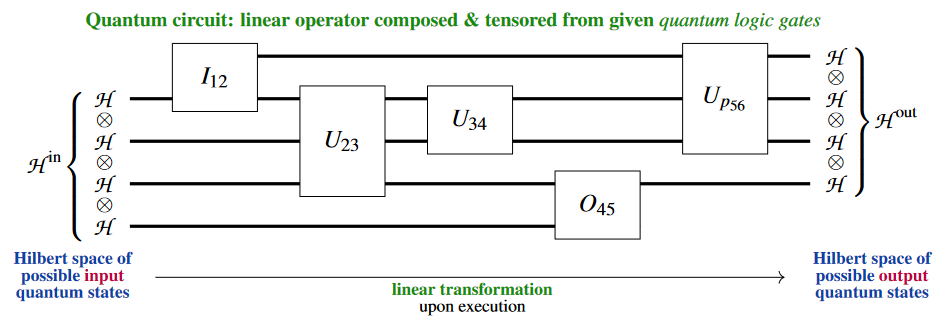
Here, for instance, the “quantum gate” $U_{34}$ is a linear operator on the tensor product Hilbert space $\mathscr{H} \oplus \mathscr{H}$.

Notice that the quantum circuit is understood to be the actual string diagram, up to the usual admissible topological deformations, not just the composite linear transformation which it encodes: The compositeness of the diagram encodes how (e.g. in which order) available quantum gate-operations would be operated on an actual quantum computer, and the composite linear map only encodes the inpute-to-output-specification of the resulting quantum computation. In this sense, quantum circuits constitute a quantum programming language and one also speaks of the “quantum circuit model of quantum computation” (e.g. Nielsen & Chuang 2000, §II.4.6; Miszczak 2011, §3, 2012, §4.3; Beneti & Casati 2018, §3.2).

Often the basic Hilbert space building block here is taken to be complex 2-dimensional, $\mathscr{H} \,\coloneqq\, \mathbb{C}^2$, in which case one speaks of a quantum circuit on q-bits.

Typically all quantum gates involved, and hence also the resulting composite linear maps, are assumed to be invertible, as befits reversible computation by unitary quantum state evolution in quantum mechanics.

But more generally and certainly in the broader context of quantum information theory (such as in formulating the quantum teleportation protocol and similar), quantum circuits are admitted to cross the quantum-classical divide?, in that they may involve:

1. quantum measurement,

2. quantum state preparation,

3. classically controlled quantum gates.

All three of these appear already in basic examples such as the quantum teleportation protocol:

Yet more generally — notably for any plausible implementation of quantum error correction — one needs to allow for quantum measurement-results to be fed back during runtime (“dynamic lifting”) into algorithms running on a universal classical computer which schedule further quantum circuit-execution, and so forth:

SQRAM model adapted from Nagarajan, Papanikolaou Williams 2007, Fig 1

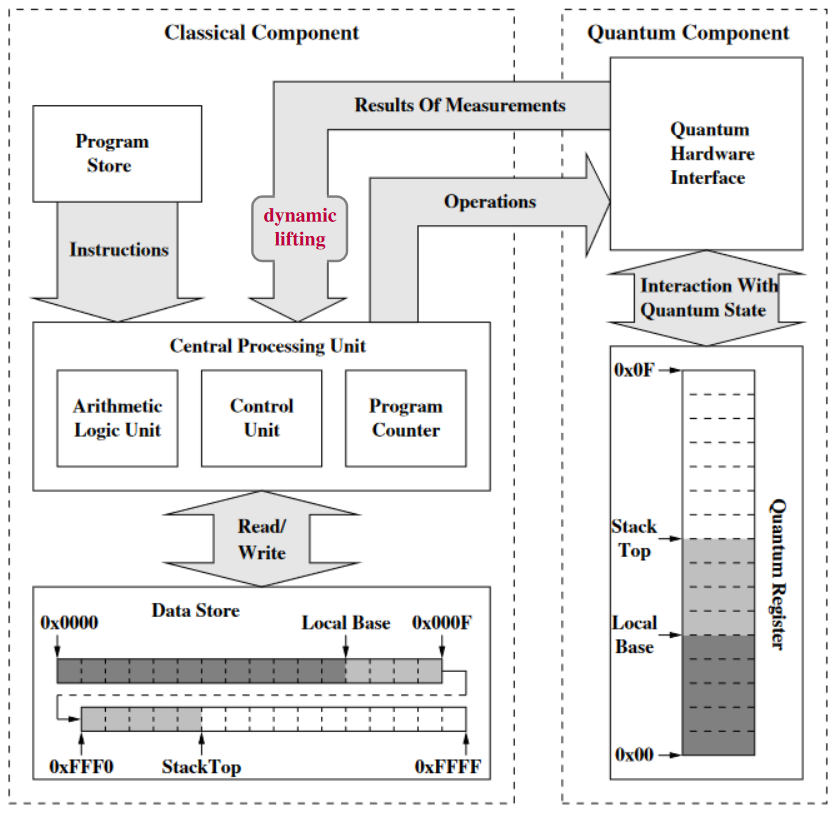
The conceptual subtlety with fully formalizing these common ideas is that quantum measurement, in particular, is not only non-reversible (due to the quantum state collapse involved) but also non-deterministic, meaning that it is not immediately represented by a fixed linear map at all – at least not between the original Hilbert spaces.

Concretely, the “projection postulate” of quantum physics asserts (von Neumann 1932; Lüders 1951) that:

1. measurement of quantum states is with respect to a choice of orthonormal linear basis $\big\{\vert \psi_b \rangle \big\}_{b : B}$ of the given Hilbert space $\mathscr{H}$ of pure quantum states;

2. the result of measurement on pure quantum states $\vert \psi \rangle \;\in\; \mathscr{H}$ is

   1. a random value $b \in B$;

   2. the “collapse” of the quantum state being measured by orthogonal projection to the the linear span of the $b$th basis state.

      $$\array{ P_b &\colon& \mathscr{H} &\xrightarrow{\phantom{---}}& \mathscr{H}_B \hookrightarrow \mathscr{H} \\ && \vert \psi \rangle &\mapsto& P_b \vert \psi \rangle \mathrlap{ = \vert \psi_b \rangle \langle \psi_b \vert \psi \rangle } }$$

There are different ways to type the quantum measurement, taking into account the non-deterministic nature of its outcome:

1. Regarding the direct sum $\bigoplus_{b \colon B} \mathscr{H}$ of Hilbert spaces as the logical disjunction (“or”) of quantum logic, one may regard measurement as being the linear map into the direct sum whose $b$th component is $P_b$.

   This choice of typing appears (briefly) in Selinger 2004, p. 39, in a precursor discussion that led to the formulation of the quantum programming language Quipper.

2. Regarding the measurement outcome $b \in B$ as the observed context of the actual quantum collapse, one may regard the collapse projection as dependently typed.

   Getting from previous option back to this one is known in the the Quipper-community as dynamic lifting (namely “of the measured bits back into the context”)

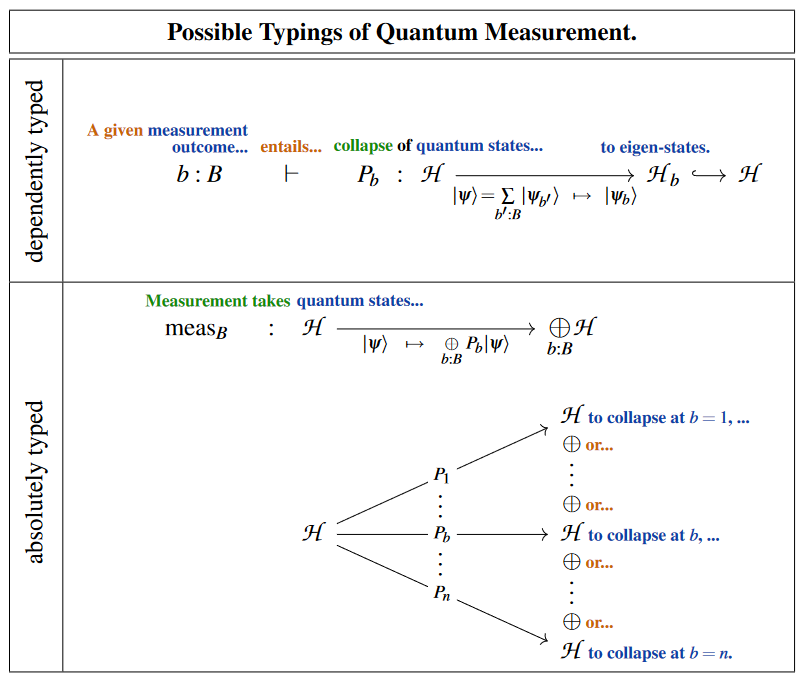
Both of these options naturally emerge and are naturally unified in the “Quantum Modal Logic” inherent to dependent linear type theory: This is what we now discuss.

A solution

The following discussion hupf indicates how a natural quantum programming language for quantum information-processing protocols — hence for quantum circuits consisting of general quantum gates with classical control, including de-coherent quantum measurement-gates and subsequent coherent quantum gates depending on these — is elegantly subsumed within any dependent linearly typed programming language which expresses the “yoga of six operations”, such as is the case in the linear homotopy type theory of Riley 2022.

This works by regarding classically controlled quantum states as having linear data types dependent on classical control parameters and on measurement results, and then making the following key observations on modal quantum logic with dependent linear types:

1. The “necessity” modality $\Box_C \coloneqq (p_C)^\ast (p_C)_\ast$ on linear types dependent on a given classical context $C$ (which includes classical control parameters as well as eventual quantum measurement-outcomes on the same footing) knows all about controlled quantum gates: These are identified just with the morphisms of the $\Box_C$-co-Kleisli category, where the $\Box_C$-counit (taking a linear type “out of the comonad”) reflects the quantum state collapse of quantum measurement, and where the $\Box_C$-comultiplication encodes the superposition-principle.

2. The external tensor product of dependent linear types gives the compilation of quantum gates into quantum circuits, essentially as familiar from the quantum string diagram-calculus of Abramsky & Coecke 2004 with respect to the plain tensor product, but now taking into account dependency on classical control and potential measurement outcomes.

All constructions and proofs here flow readily from just the six operation yoga and (co-)Kleisli theory. One key point is (?) that the necessity modality respects the external tensor product – so that these classically controlled quantum circuits are unambiguously defined –, under the assumption that it coincides with the dual possibility modality $\lozenge_C \mathscr{H}_C$ on the quantum data types $\mathcal{H}_\bullet$ involved – hence (in full generality) when the linear types are dualizable in the sense of ambidexterity and specifically (in the traditional models) when quantum state spaces are finite dimensional, as is the case in quantum information theory.

Aspects of the following have a resemblance to some variants and categorical interpretations of the quantum programming language “Quipper” (see the references there), but avoids (see below) Quipper’s problem of needing “dynamic lifting” (see there) of “measurement bits back into the context”: The linear necessity-modality knows right away that measurement outcomes are recorded in the context.

Idea: Modal quantum logic via linear homotopy types

We assume a dependent linear type theory which functorially obtains (as anticipated in Schreiber 2014, §3.2 and established in Riley 2022, §2.4):

1. from a classical (“intuitionistic”) type $X : Type$ a (large) type $LinType_X$ of linear types dependent on $X$ (cf. quantum sets), equipped with symmetric closed monoidal structure $(-) \otimes (-)$ (tensor product) and $[-,\,-]$ (internal hom);

2. from a function $f : X_1 \xrightarrow{\;} X_2$ between classical types a yoga of six operations (specifically: a “Wirthmüller context”) between their types of dependent linear types, hence a contravariant substitution/pullback operation $f^\ast$ which is strong monoidal, strong closed and extends to a base change adjoint triple (with left adjoint $f_!$ a version of dependent sum and right adjoint a version of dependent product):

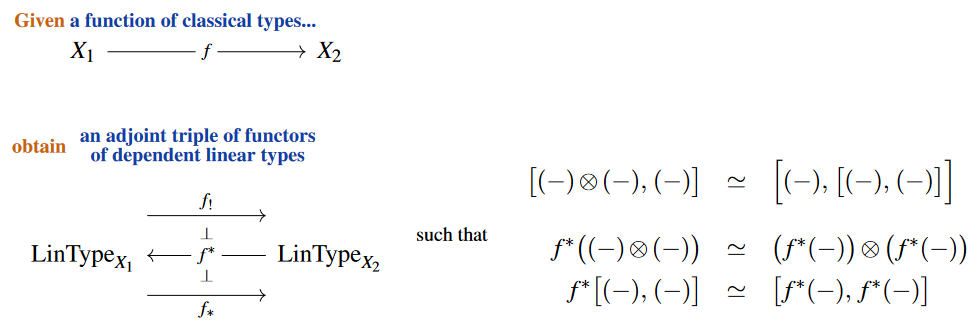
Classical modal logic

First observe that (without imposing a further condition) also classical (“non-linear”) dependent type theory provides an example of this yoga of six operations (actually five distinct operations, in the present case of Wirthmüller contexts), with:

1. tensor product given by product types,

2. internal hom given by function types,

3. $f^\ast$ given by context extension,

4. $f_!$ given by dependent coproduct,

5. $f_\ast$ given by dependent product.

In this classical situation, the (co-)monad adjoint pair $\lozenge_C \dashv \Box_C$ induced by the adjoint triple is readily found (see here) to reflect the necessity-modality and the possibility-modality of a kind of modal logic which regards the potential measurement outcomes $c : C$ as “possible worlds”:

In fact there is (see here) a quadruple of (co-)monadic modalities associated with any base change:

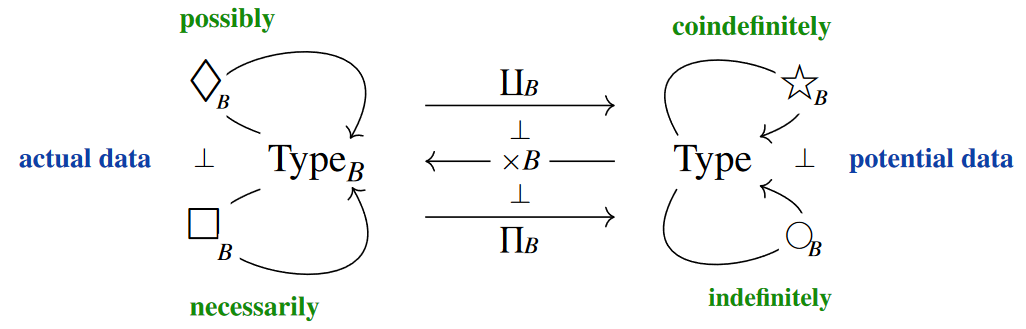
Here

1. the definiteness-modality $\star$ is also known as the writer comonad;

2. the randomness-modality $\bigcirc$ is also known as the reader monad.

We recover the meaning of these expressions in terms of quantum measurement and quantum state preparation, below.

(In general there may be richer dependency on classical contexts. In the next simplest case the base change is along the projection map out of a Cartesian product of classical types, which makes one of them label potential upcoming measurement results as before, while the other encodes further dependency on classical parameters, such as on previous measurement results:

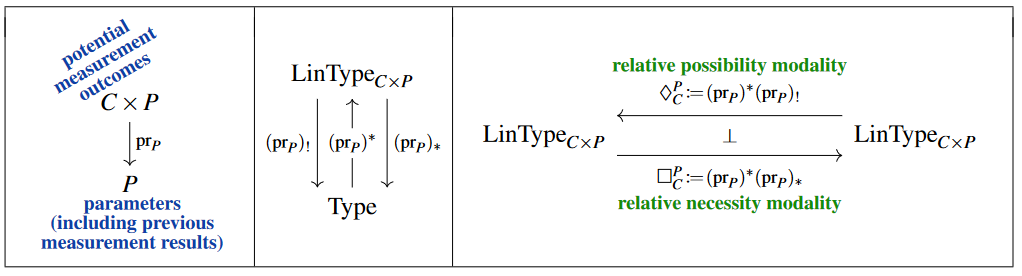
This plays a role for classically-controlled quantum gates, below).

Quantum modal logic

This general modal logic of possible worlds found inside dependent type theory becomes subject to one curious further rule as we pass to genuinely linear types, such as in the sense of stable homotopy types in linear homotopy type theory:

Namely, assuming that the potential measurement outcomes $c \colon C$ form a finite set — which is the case of relevance in quantum information theory —, the linearity or stability axiom implies that the base change down from the context $C$ becomes ambidextrous, in that on dependent linear types $\mathscr{H}_\bullet$ the coproduct computed by the possibility-modality and the product computed by the necessity-modality agree (the situation of a “biproduct”):

$$BC : FinSet ,\;\; \mathscr{H}_\bullet \,\colon\, LinType_B \;\;\;\;\; \vdash \;\;\;\;\; \lozenge \mathscr{H}_\bullet \;\simeq\; \Box \mathscr{H}_\bullet \,.$$

Curiously, in terms of modal logic, this is the Gell-Mann principle of quantum physics:

$$\array{ \llap{\text{The}}\; \text{possible} & \text{is} & \text{necessary} & \text{and hence} & \text{actualized} \\ \lozenge \mathcal{H}_\bullet & \simeq & \Box \mathcal{H}_\bullet & \xrightarrow{\phantom{--} \epsilon \phantom{--}} & \mathcal{H}_{ \bullet \; \mathrlap{\text{with some probability}} } }$$

Concretely, the linear homotopy type theory of Riley 2022 should have categorical semantics in the $\infty$-topos of parameterized $H\mathbb{C}$-module spectra (S. 2014, Ex. 3.11) and complex vector spaces embed into this stable homotopy theory under passage to their Eilenberg-MacLane spectra (see the stable Dold-Kan correspondence).

(1)$$\text{It is convenient and meaningful to declare the notational conventions to:} \phantom{--------------------}$$

1. abbreviate $\mathscr{H} \,\coloneqq\, p_! \mathscr{H}_\bullet \,\simeq\, p_\ast \mathscr{H}_\bullet$

2. notationally suppress any outer application of $(p_B)^\ast \colon LinType \to LinType_B$;

Thereby, the definiteness/randomness modalities in relation to necessity and possibility of classical modal logic (above) may be expressed in quantum modal logic by:

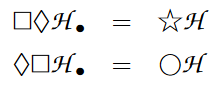
This way, the default categorical semantics for modal quantum logic is that of bundles of finite dimensional vector spaces (finite-dimensional complex Hilbert spaces) over finite sets: In this case both $(p_C)_!$ as well as $(p_C)_\ast$ yield the ordinary direct sum of the fibers (a biproduct). Since this is the categorical semantics under which the following type theory describes the traditional quantum circuits, we will adopt our notation to this case and denote the generic dependent linear type by $\mathcal{H}_\bullet : LinType_C$ and its generic term by the usual notation for quantum states:

$$c : C \;\;\; \vdash \;\;\; \vert \psi_c \rangle \;\colon\; \mathcal{H}_c \,.$$

one finds for the base change adjoint triple of dependent linear types along finite fibers (?) that the interpretation of their (co-)units is as follows:

By the assumption that $B$ is finite and since Vect has biproducts, the colimit/coproduct

$$(p_B)_! \mathscr{V}_\bullet \;=\; \coprod_{b : B} \mathscr{V}_b$$

and the limit/product

$$(p_B)_\ast \mathscr{V}_\bullet \;=\; \prod_{b : B} \mathscr{V}_b$$

agree (we have an ambidextrous adjunction) and are both equivalent to the direct sum:

$$(p_B)_! \mathscr{V}_\bullet \;\simeq\; (p_B)_\ast \mathscr{V}_\bullet \;=\; \underset{b \colon B}{\bigoplus} \mathcal{V}_b \,.$$

Accordingly, the underlying endofunctors of the induced monad and comonad on $k Vec_B$

$$\Box_B \;\coloneqq\; (p_B)^\ast (p_B)_\ast \;\;\vdash\;\; \lozenge_B \;\coloneqq\; (p_B)^\ast (p_B)_! \;\;\colon\;\; k Vec_B \longrightarrow k Vec_B$$

agree, to make a self-adjoint functor

$$(p_B)^\ast \bigotimes_B \;\;\vdash\;\; (p_B)^\ast \bigotimes_B \;\;\;\colon\;\;\; k Vec \longrightarrow k Vec$$

which carries the structure both of a monad and of a comonad.

This way, one finds that the four (co)unit operations of quantum modal logic are given as follows:

(2)

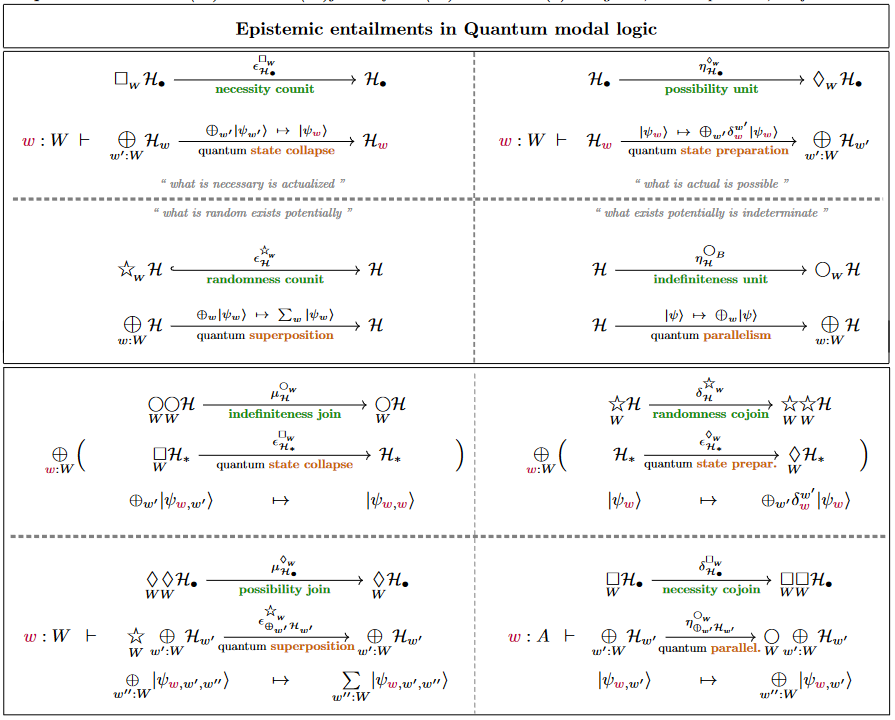
Quantum modality

In addition to the above schemata of (co)monads acting on the (dependent) linear type systems, we invoke the relative monad

$$\array{ \mathrm{Q} &\colon& Type &\longrightarrow& LType \\ && B &\mapsto& \underset{B}{\bigoplus} \mathbb{1} }$$

which sends a finite type (in particular) to the direct sum that it spans (a detailed description of this relative monad is here).

This is in fact idempotent, in that the actual monad on the full dependent linear type system that this relative monad is induced by is the idempotent monad which witnesses a reflective subcategory-inclusion of the linear types into dependent linear types:

$$\mathrm{Q} \;\colon\; Type \xrightarrow{ (-) \times \mathbb{1} } DLType \twoheadrightarrow LType \xhookrightarrow{ \phantom{---} } DLType \,.$$

This implies that whenever $D \;\colon\; LType$, we may describe morphisms of the form $\mathrm{Q}B \to LType$ by Kleisli morphisms for $\mathrm{Q}$.

For example for $B = Bit$ the type of classical bits, we have that

$$\mathrm{Q}(Bit) \;=\; QBit$$

is the usual type of q-bits.

Quantum gates

With the above modal quantum logic, we may naturally type (controlled) quantum gates as follows:

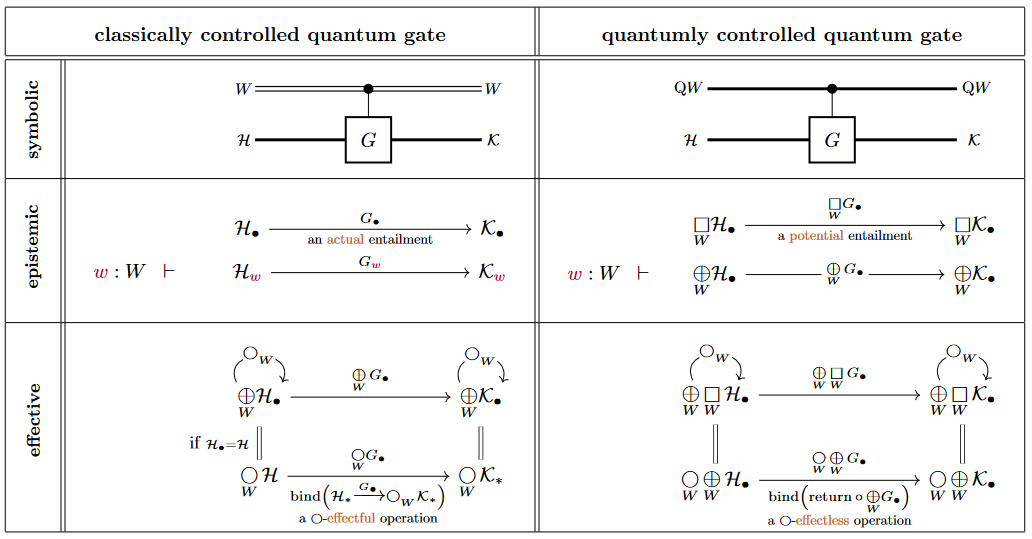
As indicated at the bottom, we may understand classically controlled quantum gates as $\bigcirc$-effectful programs (in the sense of monads in computer science).

(In the bottom left we assume that the state spaces themselves are independent of $w \colon W$, hence $\mathscr{H}_\bullet \,=\, \mathscr{H}$, which is typically the case in application.)

Next we see that the $\bigcirc$-effect handling, in this sense, is nothing but quantum measurement:

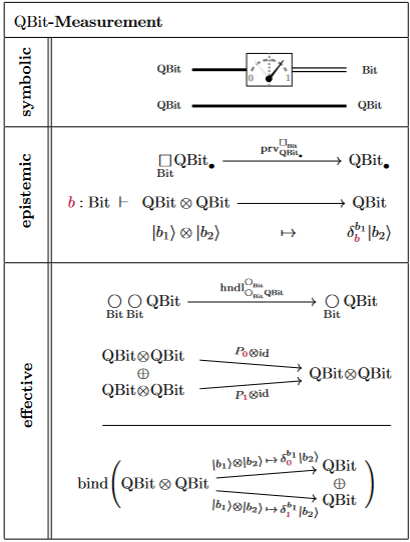
Quantum measurement

Specifically, $\Box_C$-actualization is the measurement process – in that the $\Box_C$-counit implements exactly the rule for wavefunction collapse (due to Lüders 1951, following von Neumann 1932, §III.3 and §VI) with regards to quantum measurements in the $C$-indexed basis of the total Hilbert space $\mathcal{H} \coloneqq \Box_C \mathcal{H}_\bullet$ which is encoded by its direct sum decomposition $\mathcal{H}_\bullet$:

Hence we may type quantum measurement gates as follows:

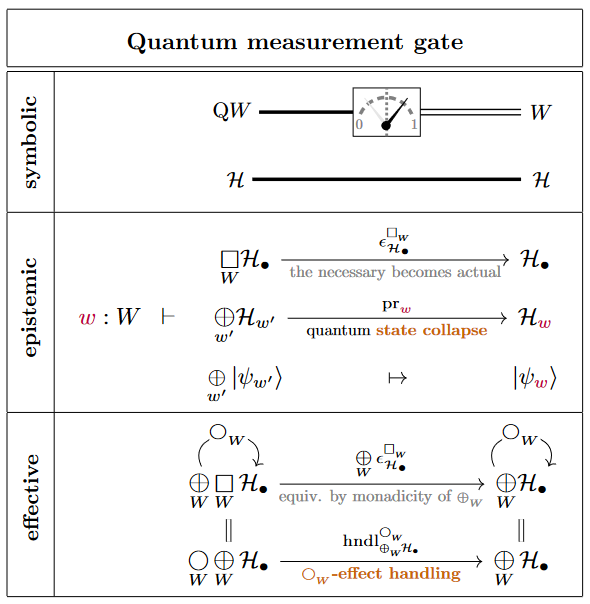
As indicated at the bottom, we may understand quantum measurement in this form as the effect handling (in the sense of monads in computer science) of indefiniteness effects (in the sense of potentiality modal logic):

Notice that this process may be understood as the “dynamic lifting” of quantum measurement-results into the context (here: $B =$ Bool) of the ambient dependent linear type theory.

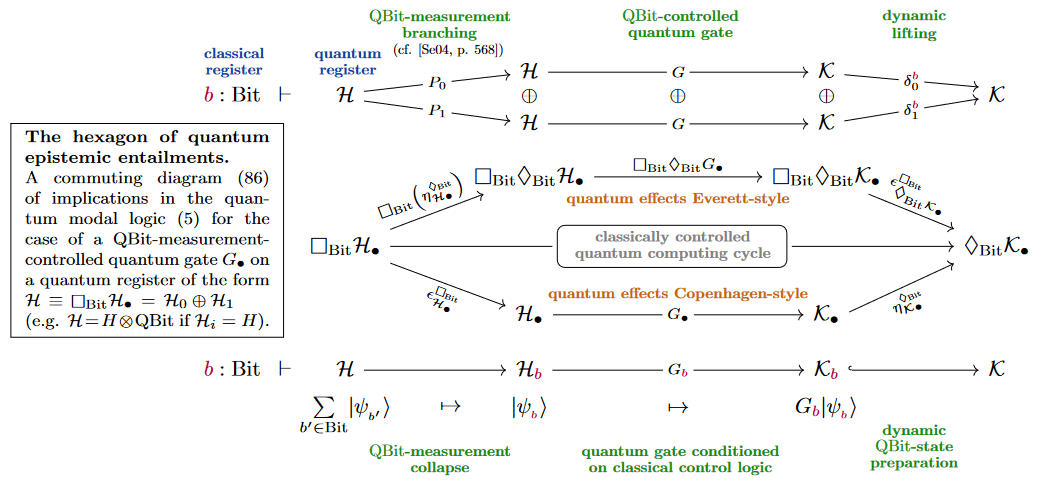
There is another possible typing of quantum measurement, where a measurement lands in the random reader monad:

These two are related by the following commuting diagram (being the naturality square of the necessity-counit on the possibility-unit, see at S5 modal logic, this remark):

(3)

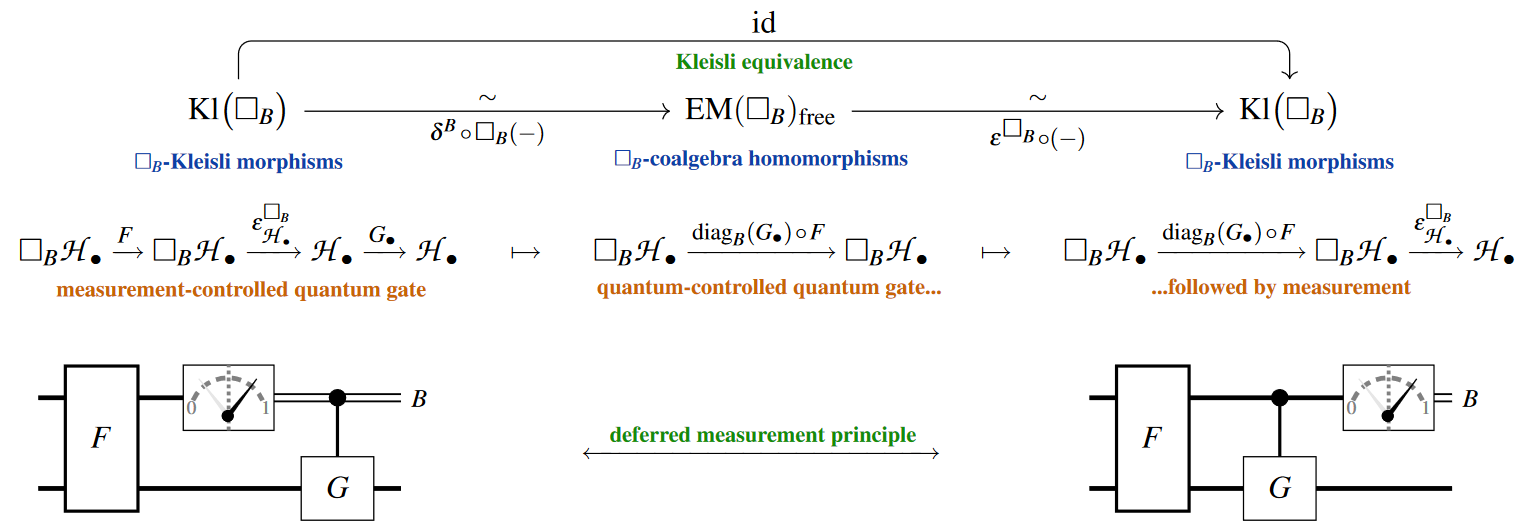
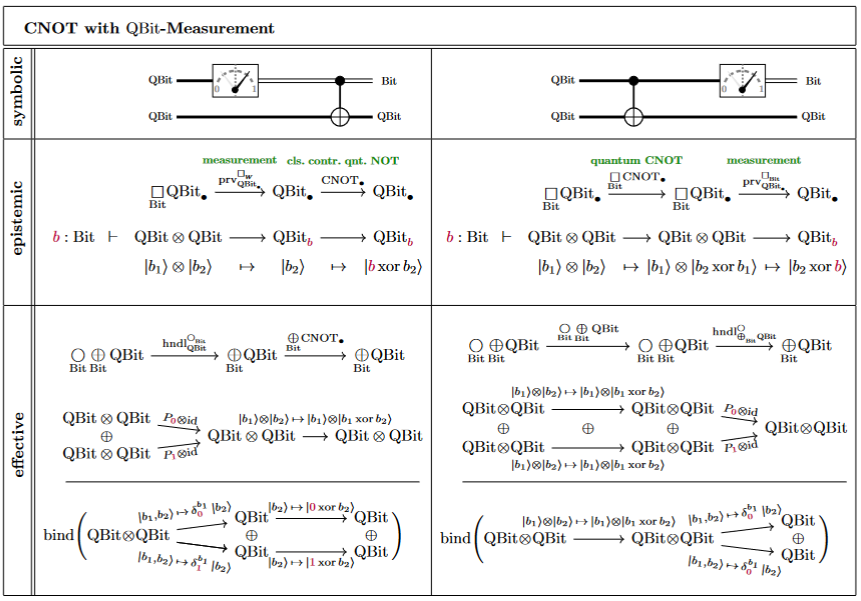
Given all this, the Kleisli equivalence for the necessity comonad $\Box_B$ is the deferred measurement principle for quantum circuits:

Example: Modal typing of basic QBit gates

We spell out in terms of the above modal quantum logic found inside dependent linear type theory the traditional zoo of quantum gates and basic quantum circuits acting on tensor products of qbits. On the one hand this serves to show how all the expected constructions are naturally recovered, on the other hand it enhances these standard concepts by what is de-facto a quantum programming language for their classically-controlled versions (as such somewhat akin to parts of Quipper)

The typing of the CNOT gate in its two incarnations as a classically or a quantumly controlled quantum gate:

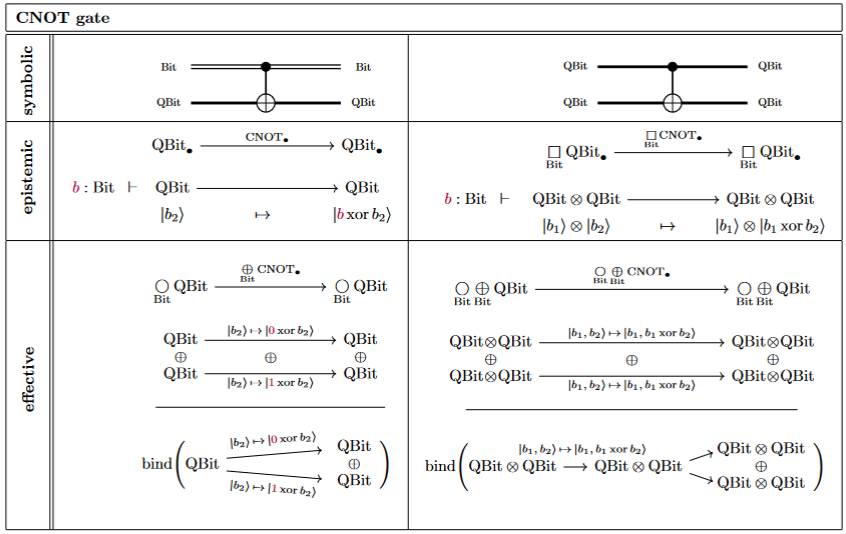
Here the quantum measurement on one $QBit$:

and their combination, in accord with the deferred measurement principle:

Quantum Programming Language

With all elements of quantum circuits formulated via (co)monads constructed inside a language of dependent linear types as above, we obtain an embedded quantum programming language for quantum circuits with classical control and effects.

Quantum/classical types and modalities

We use the following notation for the type system and the quantum/classical modalities on these.

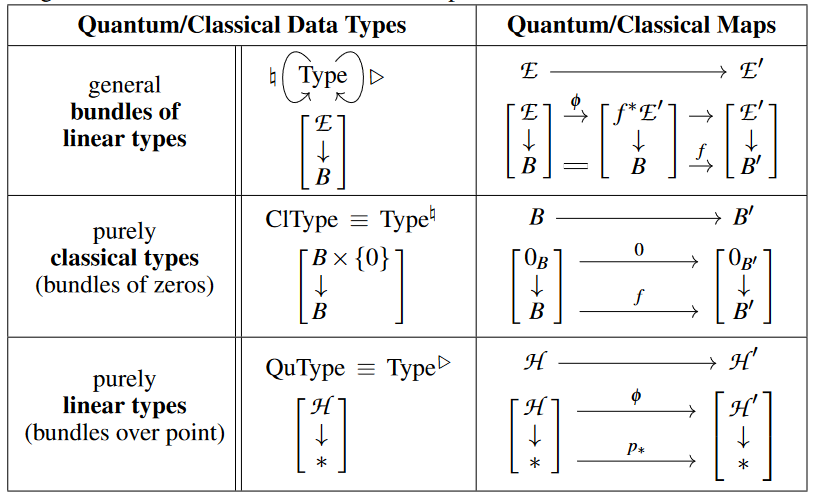
Here the expressions in square brackets may be thought of as the corresponding categorical semantics as bundles of linear types (for instance semantics in the category VectBund of complex vector bundles over Sets, or more generally, in the $\infty$-category of parametrized $H\mathbb{C}$-module spectra).

The classical modality $\natural$ and the quantum modality $\mathrm{Q}$ send a bundle type to its base and to its “linearized total space”, respectively:

(The quantum monad $\mathrm{Q}$ is a relative monad; its categorical semantics in VectBund is discussed there.)

The classical internal hom and its quantum version relative to the (“external”) linear tensor product (for more on this see the discussion here at VectBund):

Notice that all these types are bundles “in themselves”, in that we did not invoke (yet) any dependent types (semantically we speak about a total tangent $\infty$-topos, not its system of slice $\infty$-categories).

Instead, the actual $B$-dependent types that we need to reflect (“dynamic lifting” of) quantum measurement will all be viewed, indirectly, through the lens of $\bigcirc_B$-modales on the non-dependent types (view the comparison functor which here is an equivalence).

The only explicit context that we do need to consider is – besides the trivial dependency on the classical unit type $\ast$, its quantum analog namely: – dependency on the tensor unit $\mathbb{1}$. This only exception to the rule we sugar away by the following “circle-colon”-notation (which is meant to rhyme on the “$\multimap$”-notation for linear implication):

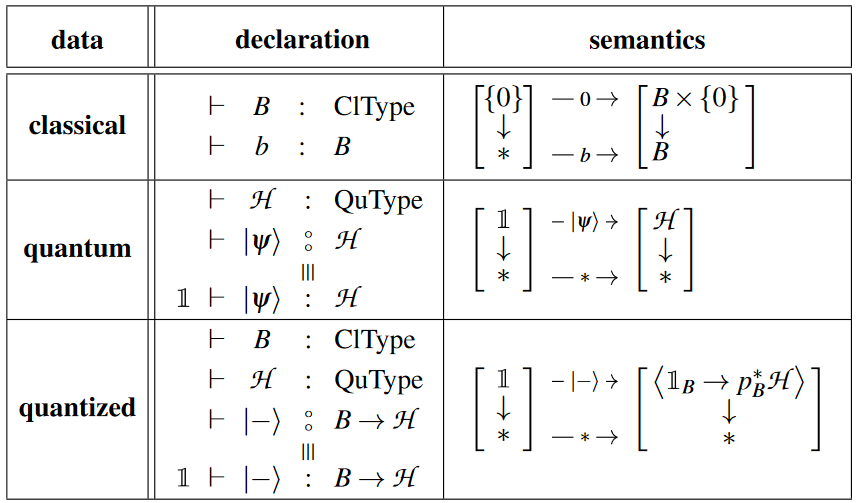
Sugaring modal dependent linear types to a quantum language

We now obtain a quantum programming language from modal dependent linear type theory simply by meticulously sugaring:

(1) the standard do-notation for monads in computer science,

(2) the (co)pure/return-functions of the various monads.

Syntax for effect binding

We code maps in the Kleisli category of an effect monad $\mathcal{E}$ by this schema:

This syntax is to closely reflect the fact that

• for an input of the form $\return^{\mathcal{E}}_D(d) \colon \mathcal{E}D$

• which may appear as a contribution in the effectful input data,

• the operation $\bind^{\mathcal{E}}_{\mathrm{prog}}$ does produce the output $\mathrm{prog}(d)$,

which prescription completely defines it.

Remark

Beware that common classical notation for exactly the same costruction is a little different:

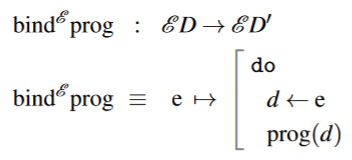
This classical notation is meant to suggest that pure data $d \colon D$ may be “read out” from effectful data $e \colon \mathcal{E}D$. While this is suggestive for the list monad and its common relatives in classical programming, it is misleading in linear type theory and notably so for the quantum monad $\mathrm{Q}$: Here the effectful input $e = \vert \psi \rangle$ is a quantum state like a q-bit, in which case $d \colon Bit$ is a classical bit, whence the classical notation “$d \leftarrow \vert \psi \rangle$” could only be suggestive of performing a quantum measurement – in contradiction to the actual nature of the resulting $\bind^{\mathrm{Q}}_{\mathrm{prog}}$-operation constituting a coherent non-measurement quantum gate.

Instead, what really happens in Kleisli formalism is that operations are defined on generators for effectful data types $\mathcal{E}(D)$, namely on data of the form $\return^{\mathcal{E}}_D(d)$. For example, the space of qbits $\vert \psi \rangle \colon \QBit$ is generated (here: linearly spanned) by the basis qbits $\vert 0 \rangle$ and $\vert 1 \rangle$, where we may naturally identify the ket-notation $\vert - \rangle$ as the unit/return operation which regards a classical bit $b$ as the corresponding basis quantum state $\vert b \rangle$.

Moreover, we write an analogous for...do-code for maps out of tensor products, using that these are generated from the homogeneous tensor products.

(…)

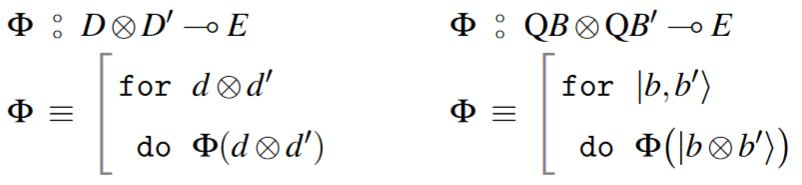
Syntax for pure effects

Finally, the monad-return operations “$`return`^{\mathcal{E}}(-)$” (and the comonad extract operations) we sugar according to the following table:

In the same vein we sugar the constructor for terms in the quantum reader monad $\bigcirc_B$ as follows:

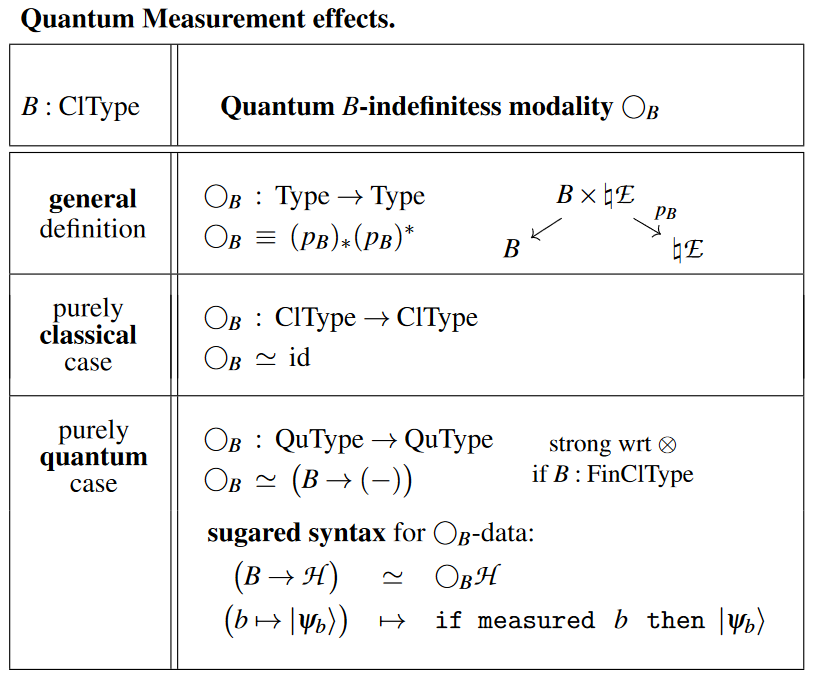
Example pseudo-code

Basic qbit circuit ingredients

Basic quantum logic gates on qbits:

The quantum NOT/Pauli X-gate

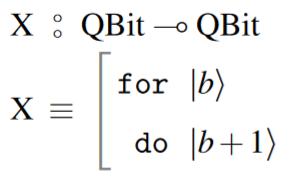
The Hadamard gate:

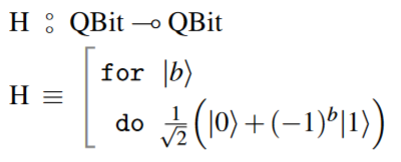
The CNOT gate:

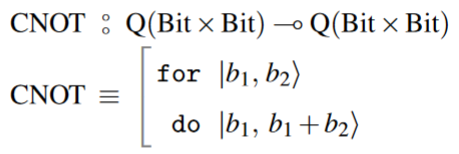
Quantum teleportation protocol

The quantum teleportation protocol:

is given by the following code:

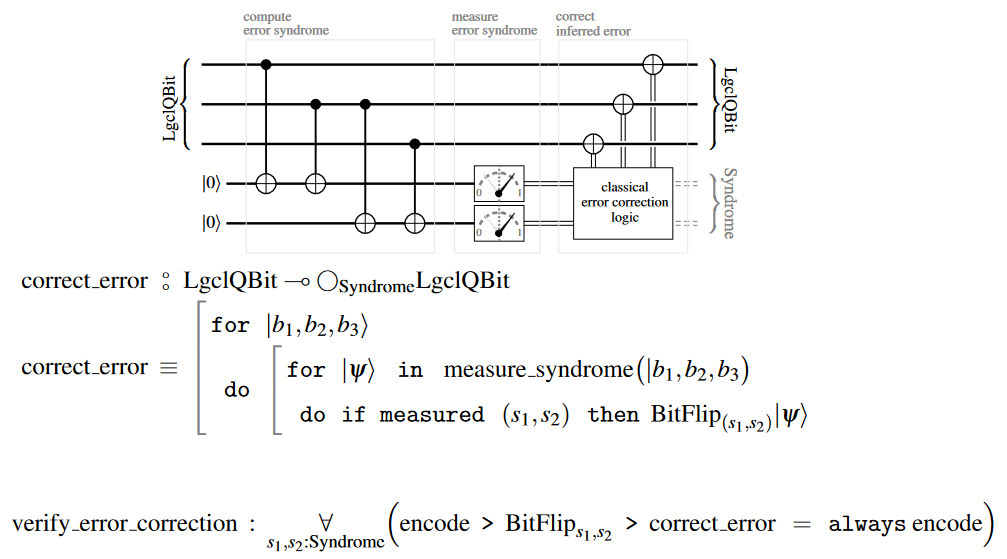
Quantum bit flip code

The quantum bit flip code for 3-qbit encoding:

References

• CQTS, Quantum Data Types via Linear HoTT, talk at Workshop on Quantum Software @ QTML 2022 (Nov 2022) [pdf]

• Hisham Sati, Urs Schreiber: The Quantum Monadology [arXiv:2310.15735]

The above figure of an SQRAM scheme is taken from:

• Rajagopal Nagarajan, Nikolaos Papanikolaou, David Williams, Simulating and Compiling Code for the Sequential Quantum Random Access Machine, Electronic Notes in Theoretical Computer Science Volume 170, 6 March 2007, Pages 101-124 [doi:10.1016/j.entcs.2006.12.014]

(…)