nLab
Mac Lane's proof of the coherence theorem for monoidal categories

Throughout, we will use the notation and terminology of Ch. VII of CWM, with the exception that the product bifunctor of a monoidal category will be denoted by $\otimes$, instead of Mac Lane’s $\square$ notation.

Introduction and statement

Let $⟨B,{\otimes }_B,{\alpha }^{(B)},e_B,{\lambda }^{(B)},{\varrho }^{(B)},⟩$ be some monoidal category. At first, we would like the coherence theorem for monoidal categories to state that every diagram in $B$ built up from instances of $\alpha$, ${\lambda }^{(B)}$, ${\varrho }^{(B)}$ and identity arrows by multiplications ${\otimes }_B$ (such as the pentagon diagram) commutes. This, however, is not possible, because some formally different vertices of such a diagram might turn out to be the same in our particular monoidal category $B$, in a way that makes the diagram non-commutative.

As a concrete example of the problem in a particular monoidal category, consider Isbell’s famous example for showing that moving to skeleta does not assure that all monoidal categories are strict (see p. 164 of CWM). In this example, one shows that if $D$ is the denumerable set in a skeleton ${\mathrm{Set}}_0$ of $\mathrm{Set}$, then, although $D\times (D\times D)$ equals $(D\times D)\times D$, the associator ${\alpha }_{D,D,D}$ (defined as usual to commute with the projections) cannot be the identity.

So, in order for coherence to work, we must change it to the statement that every ”formal” diagram commutes.
The formal diagrams that commute will be described through certain graphs $𝒢{\prime }_n$ ($n\in \mathbb{N}$). The vertices of $𝒢{\prime }_n$ will be binary words of length $n$, and its arrows will represent the sort of arrows that participate in the coherence theorem.

We begin by defining the set $W$ of binary words inductively, as the set of all terms in one variable (denoted by ”$-$”) in the signature $\{e_0,\otimes \}$, where $e_0$ is an 0-ary function symbol (a constant), and $\otimes$ is a binary function symbol. So, $W$ is the smallest set of strings in the alphabet $\{e_0,\otimes ,-\}$ satisfying $-\in W$, $e_0\in W$, and if $u,v\in W$ then $\otimes uv$ (usually written as $(u)\otimes (v)$ or even $u\otimes v$ for convenience) is also in $W$.

Next, we define a set $S\prime$ of certain arrow symbols as follows (the reason for the tag in $S\prime$ will be clear later). Let $S\prime$ be the smallest set of strings in the alphabet $W\cup \{1,\alpha ,{\alpha }^{-1},\lambda ,{\lambda }^{-1},\varrho ,{\varrho }^{-1},{\displaystyle \hat{\otimes }\}}$ satisfying $\alpha uvw,{\alpha }^{-1}uvw\in S\prime$ for all $u,v,w\in W$, $\lambda w,{\lambda }^{-1}w,\varrho w,{\varrho }^{-1}w\in S\prime$ for all $w\in W$, and for all $w\in W$, if $\beta \in S\prime$ then also $(\beta )\hat{\otimes }(1w),(1w)\hat{\otimes }(\beta )\in S\prime$ (more precisely, the last terms should be called, $\hat{\otimes }\beta 1w$ and $\hat{\otimes }1w\beta$, but as before, we will usually use the more convenient infix notation). Note that elements of $S\prime$ are comprised of a single associator/unitor symbol (or their inverses) tensored with one or more strings of the form $1w$. Later, when we will interpret the elements of $S\prime$ as arrows of a particular monoidal category $B$, we will call them basic arrows. The idea is that every arrow of the ”right” kind in $B$ (the kind considered in the coherence theorem) factors as the composition of such basic arrows (because $\otimes$ is a bifunctor).

It can be verified that every string of $S\prime$ is of one and only one of the following forms: $\alpha uvw$ for some $u,v,w\in W$, ${\alpha }^{-1}uvw$ for some $u,v,w\in W$, $\lambda w$ for some $w\in W$, …, $\beta \hat{\otimes }1w$ for some $w\in W$ and $\beta \in S\prime$. Also, in each case the ”arguments” are determined uniquely (for example, both $\beta$ and $w$ are determined from $\beta \hat{\otimes }1w$), and so we may define functions on $S\prime$ inductively.

Let $𝒢\prime$ be the directed graph (quiver in $n$Lab jargon) with $W$ as the set of objects, $S\prime$ as the set of arrows, and with the obviously defined $\mathrm{dom}$ and $\mathrm{cod}$ (for example, For $u,v,w\in W$, $\mathrm{dom}(\alpha uvw):=u\otimes (v\otimes w)=:\mathrm{cod}({\alpha }^{-1}uvw)$, $\mathrm{dom}(\beta \hat{\otimes }1w):=\mathrm{dom}(\beta )\otimes w$, etc.

Define inductively the length $\mathrm{len}(w)$ of a binary word $w$ as follows:

$$\mathrm{len}(e_0):=0,\mathrm{len}(-):=1,\mathrm{len}(u\otimes v):=\mathrm{len}(u)+\mathrm{len}(v).$$len(e_0):=0,\quad len(-):=1,\quad len(u\otimes v):= len(u) + len(v).

Since for all $s\in S\prime$, $\mathrm{len}(\mathrm{dom}(s))=\mathrm{len}(\mathrm{cod}(s))$ (this can be verified by induction), $𝒢\prime$ is the union of disjoint graphs $𝒢{\prime }_n$, where for $n\in \mathbb{N}$, the vertices of $𝒢{\prime }_n$ are the binary words of length $n$, and the edges are all $s\in S\prime$ with $\mathrm{len}(\mathrm{dom}(s))=n$.

Now, let us fix some monoidal category $⟨B,{\otimes }_B,{\alpha }^{(B)},e_B,{\lambda }^{(B)},{\varrho }^{(B)},⟩$, and some object $b\in \mathrm{obj}(B)$. We can interpret vertices and edges of $𝒢\prime$ in $B$ by defining inductively functions $(\cdot {)}_b:W\to \mathrm{obj}(B)$, $ℐ:S\prime \to \mathrm{arr}(B)$ as follows:

$$(e_0{)}_b:=e_B,(-{)}_b:=b,(u\otimes v{)}_b:=u_b{\otimes }_B{v}_b,$$(e_0)_b:=e_B,\text{ } (-)_b:=b, (u\otimes v)_b:= u_b\otimes_B v_b,

$$\begin{array}{rlr}& & ℐ(\alpha uvw):={\alpha }_{u_b,v_b,w_b}^{(B)},ℐ({\alpha }^{-1}uvw):=({\alpha }_{u_b,v_b,w_b}^{(B)}{)}^{-1},\\ & & ℐ(\lambda u):={\lambda }_{u_b}^{(B)},ℐ({\lambda }^{-1}u):=({\lambda }_{u_b}^{(B)}{)}^{-1},\\ & & ℐ(\varrho u):={\varrho }_{u_b}^{(B)},ℐ({\varrho }^{-1}u):=({\varrho }_{u_b}^{(B)}{)}^{-1},\\ & & ℐ(\beta \hat{\otimes }1w):=ℐ(\beta ){\otimes }_B{1}_{w_b},ℐ(1w\hat{\otimes }\beta ):=1_{w_b}{\otimes }_Bℐ(\beta )\end{array}$$\begin{aligned} &&\mathcal{I}(\alpha u v w) := \alpha^{(B)}_{u_b,v_b,w_b},\quad \mathcal{I}(\alpha^{-1} u v w):= (\alpha^{(B)}_{u_b,v_b,w_b})^{-1},\\ && \mathcal{I}(\lambda u) := \lambda^{(B)}_{u_b}, \quad \mathcal{I}(\lambda^{-1} u) := (\lambda^{(B)}_{u_b})^{-1},\\ && \mathcal{I}(\varrho u) := \varrho^{(B)}_{u_b}, \quad \mathcal{I}(\varrho^{-1} u) := (\varrho^{(B)}_{u_b})^{-1},\\ && \mathcal{I}(\beta\hat{\otimes} 1w) := \mathcal{I}(\beta)\otimes_B 1_{w_b},\quad \mathcal{I}(1w\hat{\otimes} \beta) := 1_{w_b}\otimes_B\mathcal{I}(\beta) \end{aligned}

(for $u,v,w\in W$ and $\beta \in S\prime$).

It is straightforward to verify that the pair $⟨(\cdot {)}_b,ℐ⟩$ is a morphism of graphs $𝒢\prime \to UB$ (where $\mathrm{UB}$ is the underlying graph of $B$), that is, that for all $s\in S\prime$, we have

$$(\mathrm{dom}(s){)}_b={\mathrm{dom}}_B(ℐ(s)),(\mathrm{cod}(s){)}_b={\mathrm{cod}}_B(ℐ(s)).$$(dom(s))_b = dom_B(\mathcal{I}(s)),\quad (cod(s))_b = cod_B(\mathcal{I}(s)).

Therefore, if $s_1,\dots ,s_m$ form a path in $𝒢\prime$ (i.e., $\mathrm{dom}(s_{i+1})=\mathrm{cod}(s_i)$ for all $i$), then $ℐ(s_1),\dots ,ℐ(s_m)$ (in that order) are composable arrows in $B$. We can finally state the coherence theorem:

Theorem

(Mac Lane’s Coherence Theorem, version 1). Let $v,w\in W$ be two binary words of the same length $n$. Suppose that $s_1,\dots ,s_m$ and $s{\prime }_1,\dots s{\prime }_{m\prime }$ form two paths from $v$ to $w$ in $𝒢{\prime }_n$. Then the two corresponding sequences of arrows in $B$ have the same composition in $B$:

$$ℐ(s_m)\circ \cdots \circ ℐ(s_1)=ℐ(s{\prime }_{m\prime })\circ \cdots \circ ℐ(s{\prime }_1)$$\mathcal{I}(s_m)\circ \cdots\circ \mathcal{I}(s_1) = \mathcal{I}(s'_{m'})\circ \cdots\circ \mathcal{I}(s'_1)

Note that at a first glance, this ”single variable coherence” looks quite limited: We only prove commutativity of diagrams in $B$ whose vertices are obtained by tensoring a single element $b$ (e.g., vertices such as $b{\otimes }_B((b{\otimes }_{B}b){\otimes }_{B}b)$). However, it turns out that the general case follows almost immediately from this case. The trick is to construct an appropriate monoidal category $\mathrm{It}(B)$ in a way that the coherence in one variable for $\mathrm{It}(B)$ and one special object of $\mathrm{It}(B)$ is the general coherence for $B$.

The coherence theorem in CWM (Theorem VII.2.1) is stated in a different way, but the main bulk of its proof is actually devoted to prove the above coherence theorem. To state also the version of Theorem VII.2.1 of CWM, let $𝒲$ be the category whose objects are binary words, with a single arrow $u\to v$ between any two binary words of the same length and with the obvious composition. The monoidal structure on $𝒲$ is the obvious one: The unit is $e_0$, and the components of the associator and the unitors are each the appropriate single arrow of the relevant hom-set. The coherence theorem in CWM is as follows:

Theorem

(Mac Lane’s Coherence Theorem, version 2). For any monoidal category $B$ and any object $b$ of $B$, there is a unique strict morphism of monoidal categories $𝒲\to B$ with $(-)\mapsto b$.

Version 2 says that $𝒲$ is the free monoidal category on one generator $(-)$ (that is, that it is the object part of a universal arrow from $(-)$ to the forgetful (object) functor ${\mathrm{Moncat}}_s\to \mathrm{Set}$, where ${\mathrm{Moncat}}_s$ stands for monoidal categories with strict morphisms of monoidal categories) . As we shall see later, this version follows almost immediately from version 1. While this is not clear at a first glance, it is also true that version 1 follows from version 2. For this, we will define a monoidal category $F[1]$ that will be almost evidently free (and hence, given version 2, isomorphic to $𝒲$).

Coherence only for the associator

It will be simpler to first prove coherence only for the associator, forgetting about the unit and the unitors. Let $𝒢$ be the full subgraph of $𝒢\prime$ whose vertex set consists only of those binary words that do not involve $e_0$. We will write $W_0$ for the subset of $W$ consisting of such binary words (that is, for the vertex set of $𝒢$).

Let $S$ be the subset of $S\prime$ consisting of the strings that
involve only instances of $\alpha$ and ${\alpha }^{-1}$ (but not $\lambda$, ${\lambda }^{-1}$, $\varrho$, and ${\varrho }^{-1}$) and also do not involve $e_0$ (e.g., as in $\alpha e_{0}vw$). Actually, $S$ could be defined inductively, similarly to $S\prime$, omitting the reference to $\lambda$, ${\lambda }^{-1}$, $\varrho$, and ${\varrho }^{-1}$, and using $W_0$ instead of $W$. Note that $S$ is the set of arrows of $𝒢$: $S=\{s\in S\prime \mid \mathrm{dom}(s),\mathrm{cod}(s)\in W_0\}$. For simplicity, we will use the same names $\mathrm{dom},\mathrm{cod}$ for the restriction of $\mathrm{dom},\mathrm{cod}$ to $S$.

Let ${𝒢}_n$ be the full subgraph of $𝒢$ on the vertices of length $n$. The proof will use a certain vertex $w^{(n)}$ of ${𝒢}_n$ as a”pivot.” Specifically, we let $w^{(n)}\in W_0$ be the unique word of length $n$ in which all pairs of parentheses start in front (e.g., $(-\otimes -)\otimes -$ for $n=3$, $((-\otimes -)\otimes -)\otimes -$ for $n=4$, and $(((-\otimes -)\otimes -)\otimes -)\otimes -$ for $n=5$; a precise inductive definition is $w^{(1)}=-$, $w^{(n)}=w^{(n-1)}\otimes -$ for $n\ge 1$).

The proof will also use a measure $\rho$ of how ”far” is a word $w\in W_0$ from being $w^{(n)}$. So, we define $\rho$ inductively by

$$\rho (-)=0,\rho (v\otimes w)=\rho (v)+\rho (w)+\mathrm{len}(w)-1.$$\rho(-) = 0, \quad \rho(v\otimes w) = \rho(v)+\rho(w)+len(w)-1.

It is easily verified that $\rho (u)\ge 0$ for all $u\in W_0$, with equality iff $u=w^{(n)}$. In fact, $\rho (u)$ is the length of the longest directed path (see ahead for what ”directed” means here) from $u$ to $w^{(n)}$. Intuitively, the idea is that if $u=v\otimes w$, then we may first handle $v$, then handle $w$, in order to reach $w^{(n_1)}\otimes w^{(n_2)}$ (with $n_1:=\mathrm{len}(v)$ and $n_2:=\mathrm{len}(w)$) but not yet to $w^{(n)}$. Then, by $n_2-1$ additional applications of associators, we finally reach $w^{(n)}$.

We will call any $s\in S$ that involves $\alpha$ a directed arrow, and any $s\in S$ that involves ${\alpha }^{-1}$ an anti-directed arrow. A more precise inductive definition is this: For all $u,v,w\in W_0$, $\alpha uvw$ is directed, and if $\beta$ is directed, then $\beta \hat{\otimes }1w$ and $1w\hat{\otimes }\beta$ are directed for all $w\in W_0$. The definition of anti-directed is obtained by replacing $\alpha$ by ${\alpha }^{-1}$ and ”directed” by ”anti-directed” in the previous definition. It can be shown by induction that if $s\in S$ is directed, then $\rho (\mathrm{cod}(s))$ is strictly smaller that $\rho (\mathrm{dom}(s))$.

For future reference, define the ”formal inverse” of $s\prime \in S\prime$ in the obvious inductive way, by setting, for example, $\mathrm{inv}(\alpha \mathrm{uvw}):={\alpha }_{u,v,w}^{-1}$, $\mathrm{inv}({\alpha }^{-1}\mathrm{uvw}):=\alpha \mathrm{uvw}$ $\mathrm{inv}(\beta \hat{\otimes }1w):=\mathrm{inv}(\beta )\hat{\otimes }1w$, etc. It can be verified that the formal inverse has all expected properties (such as being idempotent, switching domain and codomain, taking an anti-directed arrow to a directed one, and being interpreted as the inverse of the interpretation of the original arrow).

From each $w\in W_0$ of length $n$, there is a ”canonical” path, involving only directed arrows, from $w$ to $w^{(n)}$ in ${𝒢}_n$, obtained by successively moving the outermost parentheses to the left with the appropriate $\alpha$. For an example, consider the paths $\to \to$ and $\to \uparrow$ in the pentagon (5) on p. 162 of CWM. Note that if $v,w\in W_0$ are both of length $n$, then there is a path in ${𝒢}_n$ from $v$ to $w$: Take the canonical path from $v$ to $w^{(n)}$, and then extend it by reversing (using $\mathrm{inv}$) every edge of the canonical path from $w$ to $w^{(n)}$.

Given $v,w\in W_0$ of the same length $n$, our task is to show that for any path from $v$ to $w$ in ${𝒢}_n$, applying $ℐ$ to the arrows of the path and composing in $B$ results in the same arrow $v_b\to w_b$ in $B$, independently of the choice of path. In other words, we would like to prove the theorem obtained from replacing $W$ by $W_0$ and $𝒢{\prime }_n$ by ${𝒢}_n$ in the first version of the coherence theorem.

As a preparation, we start with the following degenerate case, that can be proved (as usual) by induction on $s$ and $s\prime$.

Proposition

There are no parallel directed arrows in ${𝒢}_n$: If $s,s\prime \in S$ are directed arrows with $\mathrm{dom}(s)=\mathrm{dom}(s\prime )$ and $\mathrm{cod}(s)=\mathrm{cod}(s\prime )$, then $s=s\prime$.

Now, take some path $s_1,\dots ,s_m$ from $v$ to $w$, as in

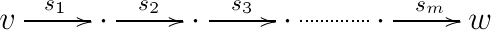
In $B$, we have the corresponding path (note that both in ${𝒢}_n$ and in $B$, it is possible that some of the vertices are in fact equal)

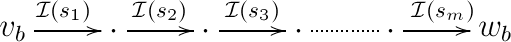
In our original path, it is possible that some arrows (some $s_i$’s) are anti-directed. We can replace each anti-directed arrow by its formal inverse so that we are left only with directed arrows. For example, if $s_2$ and $s_3$ are the only anti-directed arrows in our path, then after formally inverting them we get the following series of arrows in ${𝒢}_n$:

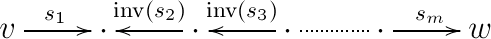
In $B$, we get

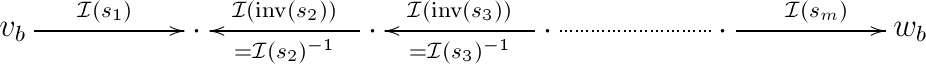
Let us write $\mathrm{can}(u)$ for the canonical path from $u\in W_0$ with $\mathrm{len}(u)=n$ and with $u\ne w^{(n)}$ to $w^{(n)}$. Let us also write $ℐ(\mathrm{can}(u))$ for the arrow of $B$ obtained by composing $ℐ$ of all arrows of $\mathrm{can}(u)$. Suppose that all squares in the following diagram of $B$ commute:

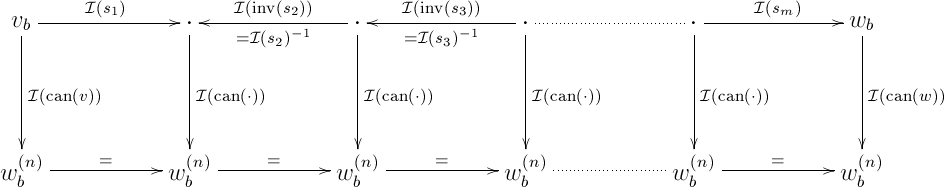
(where we write $w_b^{(n)}$ for $[w^{(n)}{]}_b$). This would imply that all squares in

commute, which also implies that the outer rectangle commutes, that is:

$$ℐ(s_m)\circ \cdots \circ ℐ(s_1)=ℐ(\mathrm{can}(w){)}^{-1}\circ ℐ(\mathrm{can}(v)).$$\mathcal{I}(s_m)\circ \cdots \circ\mathcal{I}(s_1) = \mathcal{I}(can(w))^{-1}\circ \mathcal{I}(can(v)).

The right-hand side depends only on $w$ and $v$ (and not on the particular choice of the path $s_1,\dots s_m$), which is exactly what we would like to prove. Hence, it is sufficient to show that all squares in the last but one diagram commute. For this, it is clearly sufficient to prove the following proposition:

Proposition

Let $v\in W_0$ be a word of length $n$, different from $w^{(n)}$. Then applying $ℐ$ to any two directed paths (paths consisting only of directed arrows) from $v$ to $w^{(n)}$ results in two paths in $B$ that have the same composition in $B$.

The proof is by induction on $\rho (v)$. For the basis, if $\rho (v)=0$ then $v=w^{(n)}$ and the assertion is trivial. Suppose, therefore, that $\rho (v)$>$0$ and the assertion is true for all $v\prime \in W_0$ with $\rho (v\prime )$<$\rho (v)$. For reasons that will be understood later, we will prove this part by one additional induction: on the length $\mathrm{len}(v)$.

Hence, we have to prove that if the assertion holds for all $v\prime$ of rank smaller than $r:=\rho (v)$ and for all $v\prime$ of rank $r$ and length smaller than $n$ (for $n$>$1$ – the basis for $n=1$ is trivial as then $v\prime =(-)=w^{(1)}$), then it holds also for all $v\prime$ of rank $r$
and length $n$.

From $\rho (v)$>$0$ we know that $v\ne -$, and hence there exist $u,w\in W_0$ such that $v=u\otimes w$. Consider two paths from $v$ to $w^{(n)}$. Let $\beta \in S$ be the first edge of the first path, and let $\gamma \in S$ be the first edge of the second path (so that in particular $\mathrm{dom}(\beta )=v=\mathrm{dom}(\gamma )$). Write $v\prime :=\mathrm{cod}(\beta )$ and $v″:=\mathrm{cod}(\gamma )$, so that in ${𝒢}_n$ we have

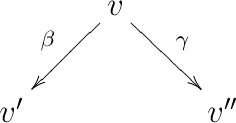
Since $\rho (v\prime )$<$\rho (v)$ and $\rho (v″)$<$\rho (v)$, by hypothesis any two paths from $v\prime$ to $w^{(n)}$ have the same composition in $B$, and similarly for $v″$. In particular, if $\beta =\gamma$, then we are done:

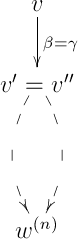
So, we will continue by assuming that $\beta \ne \gamma$. Note that in this case $v\prime \ne v″$, because it can verified by induction that there are no parallel arrows in ${𝒢}_n$. In this case, it will be sufficient to find some $z\in W_0$ of length $n$ and directed paths (recall that here a directed path is a path consisting only of directed arrows) in ${𝒢}_n$ from $v\prime$ to $z$ and from $v″$ to $z$ such that applying $ℐ$ to the following diamond (upper part of the diagram) results in a commutative diamond in $B$:

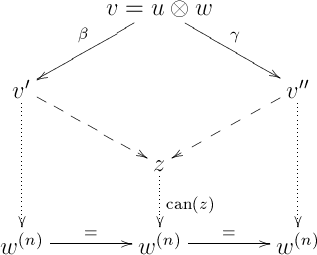
(the outer paths are our two paths from $v$ to $w^{(n)}$). This is indeed enough, because by hypothesis, the two lower trapezoids are commutative in $B$.

The existence of $z\in W_0$ and of directed paths from $v\prime$ and $v″$ to $z$ such that the above diamond is commutative in $B$ will be proved by considering all possible cases for $\beta$ and $\gamma$. For $\beta$, we have three possibilities:

• $\beta =\beta \prime \hat{\otimes }1\tilde{w}$ for some $\tilde{w}\in W_0$ and some directed $\beta \prime \in S$. In this case

$$v=u\otimes w=\mathrm{dom}(\beta )=\mathrm{dom}(\beta \prime )\otimes \tilde{w}$$v = u\otimes w = dom(\beta) = dom(\beta')\otimes \tilde{w}

and therefore $\mathrm{dom}(\beta \prime )=u$ and $\tilde{w}=w$ (by standard ”unique decomposition” of terms in a first-order language). Also, $v\prime =\mathrm{cod}(\beta )=\mathrm{cod}(\beta \prime )\otimes w$.

• $\beta =1\tilde{u}\hat{\otimes }\beta ″$ for some $\tilde{u}\in W_0$ and some directed $\beta ″\in S$. As above, we get in this case that $\mathrm{dom}(\beta ″)=w$ and $\tilde{u}=u$. Also, $v\prime =\mathrm{cod}(\beta )=u\otimes \mathrm{cod}(\beta ″)$.

• $\beta =\alpha \tilde{u}st$ for some $\tilde{u},s,t\in W_0$, in which case

$$v=u\otimes w=\mathrm{dom}(\beta )=\tilde{u}\otimes (s\otimes t),$$v = u\otimes w = dom(\beta) = \tilde{u}\otimes (s\otimes t),

so that $\tilde{u}=u$ and $w=s\otimes t$. Also, $v\prime =\mathrm{cod}(\beta )=(u\otimes s)\otimes t$.

In summary, we have the following 3 cases for $\beta$:

• Case $1_{\beta }$: $\beta =\beta \prime \hat{\otimes }1w$ for some directed $\beta \prime \in S$ with $\mathrm{dom}(\beta \prime )=u$. Also, $v\prime =\mathrm{cod}(\beta \prime )\otimes w$.

• Case $2_{\beta }$: $\beta =1u\hat{\otimes }\beta ″$ for some directed $\beta ″\in S$ with $\mathrm{dom}(\beta ″)=w$. Also, $v\prime =u\otimes \mathrm{cod}(\beta ″)$.

• Case $3_{\beta }$: $\beta =\alpha ust$ for some $s,t\in W_0$, and also $w=s\otimes t$ and $v\prime =(u\otimes s)\otimes t$.

Similarly, we have Case $1_{\gamma }$, Case $2_{\gamma }$ and Case $3_{\gamma }$ for $\gamma$. We will now consider each one of the possible cases for $\beta$ and $\gamma$:

$1_{\beta }$ and $1_{\gamma }$: The situation is as follows:

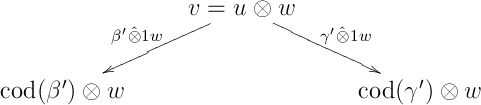
Since $\mathrm{len}(u)$<$\mathrm{len}(v)$ (as $w\in W_0$ cannot be $e_0$) and since

$$\rho (u)=\rho (v)-({\underbrace{\rho (w)}}_{\ge 0}+{\underbrace{\mathrm{len}(w)-1}}_{\ge 0})\le \rho (v),$$\rho(u) = \rho(v) - (\underbrace{\rho(w)}_{\geq 0} + \underbrace{len(w) - 1}_{\geq 0}) \leq \rho(v),

it follows from the induction hypothesis that any two directed paths from $u$ to $w^{(\mathrm{len}(u))}$ have the same composition in $B$. In particular, applying $ℐ$ to the following diamond in ${𝒢}_{\mathrm{len}(u)}$ results in a commutative diamond in $B$:

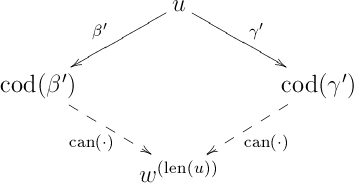
Since ${\otimes }_B$ is a bifunctor, it follows that the following diagram is again commutative when interpreted in $B$:

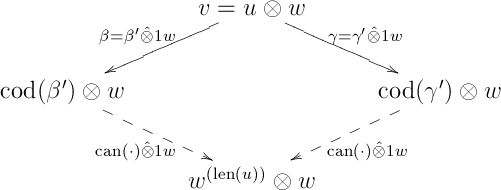
(where for $x\in W_0$ with $\mathrm{len}(x)=\mathrm{len}(u)$, we write $\mathrm{can}(x)\hat{\otimes }1w$ for the directed path in ${𝒢}_n$ obtained by $\hat{\otimes }$-ing each arrow of $\mathrm{can}(x)$ from the right with $1w$). This completes the proof for the current case.

$2_{\beta }$ and $2_{\gamma }$: Proved similarly to the previous case.

$1_{\beta }$ and $2_{\gamma }$ (or $2_{\beta }$ and $1_{\gamma }$): We have the following diamond:

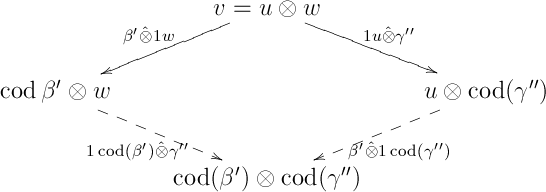
which commutes in $B$, because ${\otimes }_B$ is a bifunctor.

$3_{\beta }$ or $3_{\gamma }$: W.l.o.g., we will assume $3_{\beta }$. Note that in this case, it is not possible that also $3_{\gamma }$ holds, that is, that $\gamma =\alpha us\prime t\prime$ for some $s\prime ,t\prime$ with $w=s\prime \otimes t\prime$, for then $s\prime \otimes t\prime =s\otimes t$, which implies that $s\prime =s$ and $t\prime =t$, so that $\gamma =\beta$, contradicting our assumption. So, we have to consider only $1_{\gamma }$ and $2_{\gamma }$. For $1_{\gamma }$, we have $\gamma =\gamma \prime \hat{\otimes }1{\underbrace{s\otimes t}}_w$ and $\mathrm{dom}(\gamma \prime )=u$, and we get the following diamond:

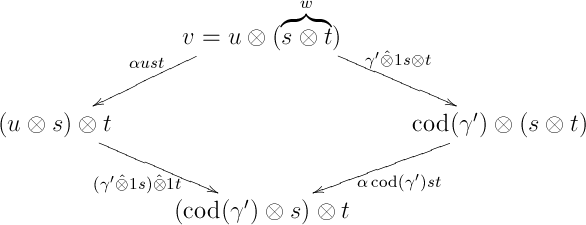
which commutes in $B$ by the naturality of ${\alpha }^{(B)}$.

For $2_{\gamma }$ ($\gamma =1u\hat{\otimes }\gamma ″$ and $\mathrm{dom}(\gamma ″)=w=s\otimes t$), we have to consider the three possible cases for $\gamma ″$.

If $\gamma ″=1\tilde{s}\hat{\otimes }\delta$ for some $\tilde{s}\in W_0$ and some directed $\delta \in S$, then by comparing domains we get $s\otimes t=\mathrm{dom}(\gamma ″)=\tilde{s}\otimes \mathrm{dom}(\delta )$, which implies that $\tilde{s}=s$ and $\mathrm{dom}(\delta )=t$, that is, $\gamma ″=1s\hat{\otimes }\delta$ with $\mathrm{dom}(\delta )=t$. Hence we get the diamond

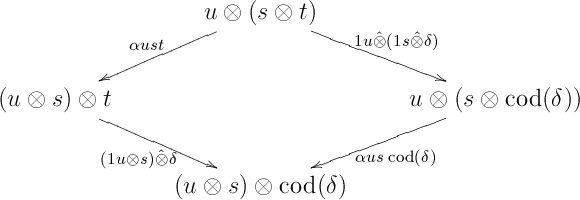
which commutes in $B$, because ${\alpha }^{(B)}$ is natural.

The case where $\gamma ″=\delta \hat{\otimes }1\tilde{t}$ for some $\tilde{t}\in W_0$ and some directed $\delta \in S$ can be treated similarly.

Finally, if $\gamma ″=\alpha rpq$, then by comparing domains we get $s\otimes t=\mathrm{dom}(\gamma ″)=r\otimes (p\otimes q)$, and therefore $r=s$ and $t=p\otimes q$. Hence, $\gamma ″=\alpha spq$ and $t=p\otimes q$. In this case, the two first edges $\beta$, $\gamma$ in our two paths from $v$ to $w^{(n)}$ look like part of the coherent pentagon (Eq. (5) on p. 162 of CWM):

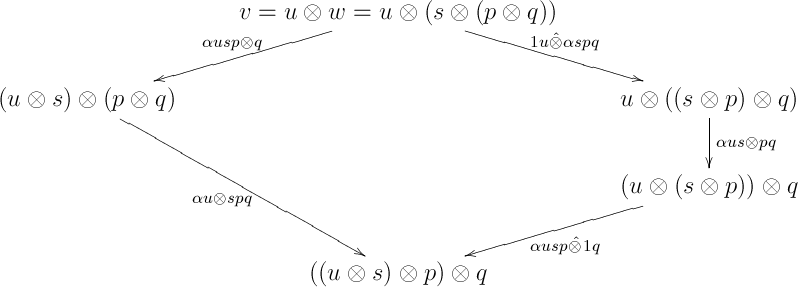
All edges in the above pentagon are directed, and the diagram is obviously commutative in $B$ (as $B$ is monoidal). This completes the proof of the proposition.

Including the unit and the unitors

Note: By Kelly’s 1964 paper, we know that the pentagon identity and one triangle identity are all that is required (that the two other triangle identities follow from the above is shown both in CWM an in Kelly, while the fact that ${\lambda }_{e_B}^{(B)}={\varrho }_{e_B}^{(B)}$ follows from the pentagon and the triangle identities is proved in Kelly). From this point on, we will be using freely all identities from pp. 162-163 of CWM.

Still need to fill this. The following are the highlights.

First, show that any directed path in path in $𝒢{\prime }_n$ may be replaced by a path with the same starting and ending vertices in which all associators (if any) are at the end, and with the same composition in $B$ as the original path. The main ingredient in the following proposition:

Proposition

Let

$$u\stackrel{s\prime }{\to }u\prime \stackrel{s″}{\to }u″$$u \stackrel{s'}{\to} u' \stackrel{s''}{\to} u''

be two directed arrows of $𝒢{\prime }_n$ with an associator appearing in $s\prime$ and a unitor appearing in $s″$ (note: the definition of ”directed” is extended in an obvious way to include unitors). Then either there exists a directed arrow $u\stackrel{s_1}{\to }u″$ containing a unitor with $ℐ(s_1)=ℐ(s″)\circ ℐ(s\prime )$, or there exist directed $s_1$, $s_2$ as in

$$u\stackrel{s_1}{\to }?\stackrel{s_2}{\to }u″$$u \stackrel{s_1}{\to} ? \stackrel{s_2}{\to} u''

with $s_1$ containing a unitor, $s_2$ containing an associator, and $ℐ(s_2)\circ ℐ(s_1)=ℐ(s″)\circ ℐ(s\prime )$.

This proposition may be proved by a long and tedious induction on $s\prime$ and $s″$.

For this I needed the triangle identities and the naturality of ${\alpha }^{(B)}$ (as mentioned in CWM), but also the naturality of ${\varrho }^{(B)}$ and ${\lambda }^{(B)}$, as well as the bifunctoriality of ${\otimes }_B$. For example, consider:

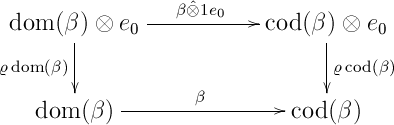
(where some associator appears in $\beta$). So – what am I missing here?

Recall that our original goal is to show that any two paths in $𝒢{\prime }_n$ with the same starting vertex and the same ending vertex have the same composition in $B$. There is still a path from any vertex of $𝒢{\prime }_n$ to $w^{(n)}$ (first remove all units, then proceed as in the case of ${𝒢}_n$), and we can use exactly the same method used above (when only the associator was considered) to reduce the problem to: Any two directed paths of $𝒢{\prime }_n$ starting at some vertex $v$ and ending at $w^{(n)}$ have the same composition in $B$. From what we have seen above, any two arbitrary such paths may be replaced be two paths starting with unitors and ending with associators, as in

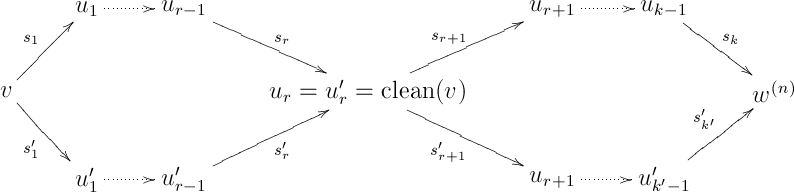
Here, $\mathrm{clean}(v)$ is the word obtained by removing all instances of the unit from $v$ (this can be defined rigorously by induction), and $r$ is the total number of units appearing in $v$. The right part of the last diagram, where there are no units and unitors, commutes in $B$ by the ”coherence for the associator” that was already proved. Hence, it remains to prove that the left part, where all arrows involve unitors, commutes in $B$ (”coherence for the unitors”).

First one must prove that two parallel directed arrows with unitors in $𝒢{\prime }_n$ have the same interpretation in $B$ .
Recall that in ${𝒢}_n$ (no units and no unitors), there are no parallel directed arrows. However, this is not the case in $𝒢{\prime }_n$ (for example, consider $\lambda e_0\otimes e_0,1e_0\hat{\otimes }\lambda e_0,1e_0\hat{\otimes }\varrho e_0:e_0\otimes (e_0\otimes e_0)\rightrightarrows e_0\otimes e_0$). Hence, we must settle for equality of the interpretations in $B$.

For this, I used induction on the total number of $\hat{\otimes }$ in both $s$ and $s\prime$, using ${\varrho }_{e_B}^{(B)}={\lambda }_{e_B}^{(B)}$ and the naturality of ${\varrho }^{(B)}$ and ${\lambda }^{(B)}$. Am I missing something here? Is there an obvious one-line argument that I’m failing to see?

Now, we can finally prove coherence for the unitors, by induction on the number $r$ of units in $v$. Considering the left part of the last diagram, if $u_1=u{\prime }_1$, as in

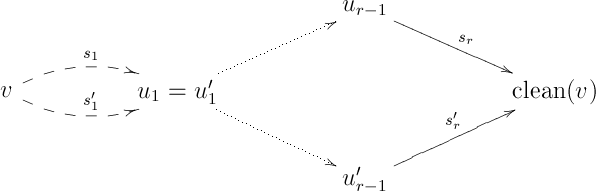
then the parallel arrows are equal in $B$, while the ”large diamond” on the right commutes in $B$ by the induction hypothesis.

We can therefore assume that $u_1\ne u{\prime }_1$. As in the case of coherence for the associator, it is sufficient to
find a commutative diamond, that is, to find some vertex $w$ of $𝒢{\prime }_n$ and directed arrows $\gamma$ and $\gamma \prime$ in $S\prime$ containing unitors, as in

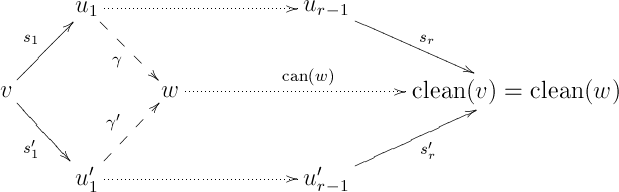
such that the diamond on the left commutes in $ℬ$:
If we find such $w$, $\gamma$ and $\gamma \prime$, then since by the induction hypothesis the upper and lower parallelograms on the right commute in $B$, we are done.

Finally, the required commutative diamond may be found by induction on $v$.

Proof of version 2 of the coherence (Theorem VII.2.1 of CWM)

I intend to come back and fill this. The most difficult part was already proved above.

The construction of $F[1]$ and proof of universality

The category $𝒲$ has one-element hom-sets by construction, but it was not at all obvious that it is indeed the free monoidal category on one generator. Alternatively, it is possible to construct a category $F[1]$ that will be almost obviously a free monoidal category on one generator. This would mean that $F[1]$ is isomorphic to $𝒲$, and in particular has one-element hom-sets. The fact that $F[1]$ is free and has one-element hom-sets may then serve as yet a third version of coherence.

This should still be filled.

Moving from one variable to any number of variables: The category $\mathrm{It}(B)$

This should still be filled.

References

• Saunders Mac Lane, Categories for the Working Mathematician, 2nd edition, Springer GTM, 1998.

• Tom Leinster Monoidal Categories, Lecture 8 of An ABC of Category Theory, Autumn 2004. available online

• Max Kelly On MacLane’s conditions for coherence of natural associators, commutativities, etc., Journal of Algebra, 1, pp. 397–402, 1964.

• I. Beylin and P. Dybjer, Extracting a proof of coherence for monoidal categories from a formal proof of normalization of monoids, available online

• P. Etingof, S. Galeki, D. Nikshych, and V. Ostrik, Tensor Categories, course notes available online

• J. Armstrong, Mac Lane’s coherence theorem