nLab rigid monoidal category

Idea

A rigid (monoidal) category, also called an autonomous (monoidal) category is a kind of category with duals. In particular, a rigid monoidal category is a monoidal category in which every object $A$ has a dual object $A^*$.

Depending on whether these duals exist on the right or the left we call the category left rigid or right rigid. Sometimes rigid refers to categories with duals on both sides.

It is important to note that every right/left rigid category can be fully embedded into a category with duals on both sides, by repeatedly applying the double dual functor and taking a colimit (see e.g. Selinger 2011, Proposition 4.7).

Definition

A monoidal category is right rigid (or right autonomous) if every object has a right dual. Similarly, a monoidal category is left rigid (or left autonomous) if every object has a left dual. A monoidal category is autonomous (sometimes called rigid) if duals exist on both sides.

Conventions differ regarding which type of duals are which. One convention is as follows: a right dual of an object $A$ in a monoidal category $\mathscr{C}$ is an object $A^*$ equipped with evaluation/co-evaluation maps

$$\text{ev}_{A}:A\otimes A^*\to 1,\,\, \text{coev}_{A}:1\to A^*\otimes A$$

where $1$ is the tensor unit, subject to the triangle identities (snake diagrams)

$$(\text{ev}_A\otimes \text{id}_A)\circ (\text{id}_A\otimes \text{coev}_{A})=\text{id}_{A},$$

$$(\text{id}_{A^*}\otimes \text{ev}_{A})\circ ( \text{coev}_{A}\otimes \text{id}_{A^*})=\text{id}_{A^*}.$$

A left dual is an object $A^*$ paired with morphisms $\text{ev}_A:A^*\otimes A\to 1$ and $\text{coev}_A:1\to A\otimes A^*$ satisfying the dual conditions.

Examples

The canonical example of a rigid category is the category $\text{Vec}_k$ of finite dimensional vector spaces over a field $k$. Namely, given a vector space $V$ the standard dual $V^*=\text{Hom}_k(V,k)$ serves as a categorical dual for $V$. Explicitly we have the following:

Proposition

Let $k$ be a field. For every vector space $V\in \text{Vec}_k$, define the maps

$$\text{ev}_V: V\otimes V^*\to k$$

$$(v,\varphi)\mapsto \varphi(v)$$

and

$$\text{coev}_V: k\to V^*\otimes V$$

$$x\mapsto x\cdot \sum_{i\in I}\varphi_i\otimes v_i$$

where $\{v_i\}_{i\in I}$ is a basis for $V$, and $\varphi_i$ is a dual basis. That is, $\varphi_i$ is defined by

$$\varphi_i(v_j)= \begin{cases} 1 & i=j\\ 0 & \text{otherwise}. \end{cases}$$

These formulas give well defined $\text{Vec}_k$-morphisms. Moreover, the satisfy the snake identities and hence give $\text{Vec}_k$ the structure of a (right) rigid category.

Proof

To begin, we verify that the definition of $\text{coev}$ is independent of basis. Suppose $\{\tilde{v}_i\}_{i\in I}$ is a different choice of basis. There is a change of basis matrix $c=(c_{i,j})_{(i,j)\in I\times I}$ between them. It is straightforward to see that the dual bases are related by the change of basis matrix $c^{-1}$. Expanding, we thus find that

$$\sum_{i}\tilde{v}_i\otimes \tilde{\varphi}_i=\sum_{i}\left(\sum_{j}c_{i,j}\cdot v_i\right)\otimes \left(\sum_{k}(c^{-1})_{k,i}\cdot \varphi_i\right)$$

$$=\sum_{j,k} \left(\sum_{i}c_{i,j}(c^{-1})_{k,i}\right)\cdot v_i\otimes \varphi_i.$$

The definition of the inverse matrix says that $\sum_{i}c_{i,j}(c^{-1})_{k,i}=\begin{cases}1 & j=k \\ 0 &\text{otherwise}\end{cases}$. Hence, we conclude that

$$\sum_{i}\tilde{v}_i\otimes \tilde{\varphi}_i=\sum_{i}v_i\otimes \varphi_i,$$

so $\coev_{V}$ is well defined as desired. We now show that the rigidity diagrams commute. Going around the square, we find that this is equivalent to the condition that $1\otimes w=\sum_{i}\varphi_i(w)\otimes v_i$ for all $w\in V$. This follows from choosing a basis such that $v_i=w$ for some $i$. Then, $\varphi_i(w)\otimes v_i=w$ and all the other terms are zero, making the equality obvious.

Another key example is that of endofunctor categories. Given any category $\mathscr{C}$, the hom-space of functors $\text{Fun}(\mathscr{C},\mathscr{C})$ is a monoidal category, with the monoidal structure coming from composition. Duals correspond to adjoint functor as can be stated formally below:

Proposition

Let $\mathscr{C}$ be a category, and let $F\in \text{Fun}(\mathscr{C},\mathscr{C})$ be an endofunctor. Let $F^*$ be the right adjoint of $F$. $F^*$ is a right dual for $F$, under the natural transformations

$$\text{ev}_{F}:F\otimes F^*\to \text{id}_{\mathscr{C}}$$

$$F(F^*(A))\xrightarrow{\text{id}_{F^*(A)}} A,\,\, A\in \mathscr{C}$$

where we here make the implicit identification

$$\text{Hom}_{\mathscr{C}}(F(F^*(A)),A)\cong\text{Hom}_{\mathscr{C}}(F^*(A),F^*(A))$$

using adjointness, and

$$\text{coev}_{F}:\text{id}_{\mathscr{C}}\to F\otimes F^*$$

$$A\xrightarrow{\text{id}_{F(A)}} F^*(F(A)),\,\, A\in \mathscr{C}$$

where we here make the implicit identification

$$\text{Hom}_{\mathscr{C}}(A,F^*(F(A)))\cong\text{Hom}_{\mathscr{C}}(F(A),F(A))$$

using adjointness. Conversely, if $F^*$ is a right dual for an endofunctor $F$ then $F^*$ is a right adjoint for $F$.

Proof

Verifying the details is straightforward.

Graphical language

Rigid categories are best expressed using the language of string diagrams. That is, we can write the rigidity axioms as

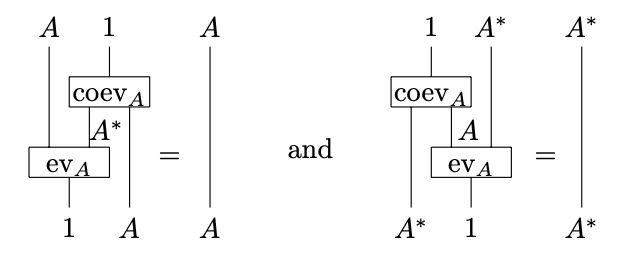
Even better, we often fix graphical notation for $\text{ev}$ and $\text{coev}$ which makes these axioms even simpler to write out:

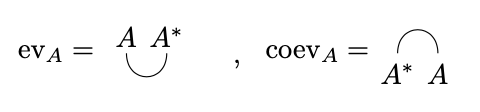
We can now express rigidity as follows:

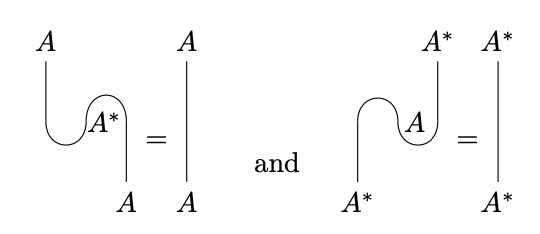
Rigidity is thus graphically the statement that string diagrams can be “straightened out”. This approach is taken, for example, in Selinger.

Remarks

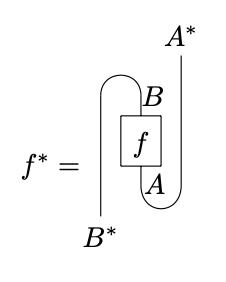
Note that this definition only asserts the existence of the dual objects. It does not assert that specific duals have been chosen. However, the choice of duals is unique up to unique isomorphism, justifying reference to ‘the’ dual of an object; in fact, this extends to a contravariant anafunctor ${}^*\colon M \to M$. (Using the axiom of choice to pick duals for every object at once, we can make this into a strict functor.) This functor is defined explicitly by the formula

$$f^*:A^*\xrightarrow{\text{coev}_B\otimes \text{id}_{A^*}} B^*\otimes B\otimes A^*\xrightarrow{\text{id}_{B^*}\otimes f\otimes \id_{A^*}} B^*\otimes A\otimes A^* \xrightarrow{\text{id}_{B^*}\otimes \text{ev}_A} B^*$$

This formula is clearer when written graphically:

Additionally, this definition does not assert that the right dual of an object is isomorphic to its left dual: this need not be the case in general, though it is true in a braided monoidal category, and thus automatically also in a symmetric monoidal category (this last fact can be considered an algebraic form of the “Whitney trick” for knots; see this MO discussion). Left duals and right duals are also isomorphic in a semisimple category. Note that a rigid monoidal category which is also symmetric is sometimes called compact closed, or simply “compact”.

In practice, algebraic geometers are the most frequent users of the term ‘rigid’, and they focus on the symmetric monoidal case, so they ignore the difference between right and left duals.

Properties

Tannaka duality

The statement of Tannaka duality for associative algebras says that rigid monoidal categories equipped with a fiber functor are categories of modules over a Hopf algebra.

Tannaka duality for categories of modules over monoids/associative algebras

monoid/associative algebra	category of modules
$A$	$Mod_A$
$R$-algebra	$Mod_R$-2-module
sesquialgebra	2-ring = monoidal presentable category with colimit-preserving tensor product
bialgebra	strict 2-ring: monoidal category with fiber functor
Hopf algebra	rigid monoidal category with fiber functor
hopfish algebra (correct version)	rigid monoidal category (without fiber functor)
weak Hopf algebra	fusion category with generalized fiber functor
quasitriangular bialgebra	braided monoidal category with fiber functor
triangular bialgebra	symmetric monoidal category with fiber functor
quasitriangular Hopf algebra (quantum group)	rigid braided monoidal category with fiber functor
triangular Hopf algebra	rigid symmetric monoidal category with fiber functor
supercommutative Hopf algebra (supergroup)	rigid symmetric monoidal category with fiber functor and Schur smallness
form Drinfeld double	form Drinfeld center
trialgebra	Hopf monoidal category

2-Tannaka duality for module categories over monoidal categories

monoidal category	2-category of module categories
$A$	$Mod_A$
$R$-2-algebra	$Mod_R$-3-module
Hopf monoidal category	monoidal 2-category (with some duality and strictness structure)

3-Tannaka duality for module 2-categories over monoidal 2-categories

monoidal 2-category	3-category of module 2-categories
$A$	$Mod_A$
$R$-3-algebra	$Mod_R$-4-module

Free rigid monoidal categories

The inclusion of the 2-category of monoidal categories into the 2-category of rigid monoidal categories admits a left 2-adjoint functor? $L$.

Furthermore, the unit of the adjunction is a strong monoidal fully faithful functor, i.e., any monoidal category $C$ admits a fully faithful strong monoidal functor $C\to L(C)$, where $L(C)$ is a rigid monoidal category.

See Theorems 1 and 2 in Delpeuch.

References

• N. Saavedra Rivano, “Catégories Tannakiennes.” Bulletin de la Société Mathématique de France 100 (1972): 417-430. EuDML

• Antonin Delpeuch, Autonomization of monoidal categories, arXiv, doi.

• Peter Selinger, A survey of graphical languages for monoidal categories, New structures for physics, arXiv

Related concepts

• star-autonomous category

• (∞,n)-category with duals

• natural language syntax

• pregroup grammar