nLab pivotal category
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Contents
Definition
A pivotal category is an autonomous category equipped with a monoidal natural isomorphism . Pivotal categories have also been called “sovereign categories.” This is a kind of category with duals.
A right autonomous category with such an isomorphism is automatically left autonomous too, so the right/left distinction does not apply to pivotal categories. Note additionally that for the double dual to really be a functor we are assuming that every object has a distinguished dual element.
Intuition
In an autonomous category , left duals and right duals have no reason to agree. That is, given an object we may not necessarily have (See this MO post for a discussion). Even if we do (like in semisimple categories and braided monoidal categories) there is no a-priori reason for this isomorphism to be natural.
For this isomorphism to be natural we need a pivotal structure. Interestingly enough, if a pivotal structure exists then it will be unique up to precomposing with an element of the group of monoidal natural automorphisms of the identity (Bartlett, Prop. 5.7, Lemma 6.2).
In the case of fusion categories, we have that where is the universal grading group. Hence, there will be only finitely many choices of pivotal structures by a result of Gelaki.
Explicit compatibility conditions
Our intuition for pivotal categories is that right duals should also be left duals in a natural/compatible way. This can be made explicit, and gives an alternative definition of pivotal. Namely, a pivotal category is a (right) rigid monoidal category equipped with morphisms
giving the structure of a left dual for , such that ,,, satisfy appropriate compatibility conditions. The exact conditions feel unmotivated and clunky when written out explicitly in terms of compositions, and hence they are best stated in the language of string diagrams.
Proposition
Let be a pivotal category, with natural isomorphism . We graphically define the distinguished morphisms
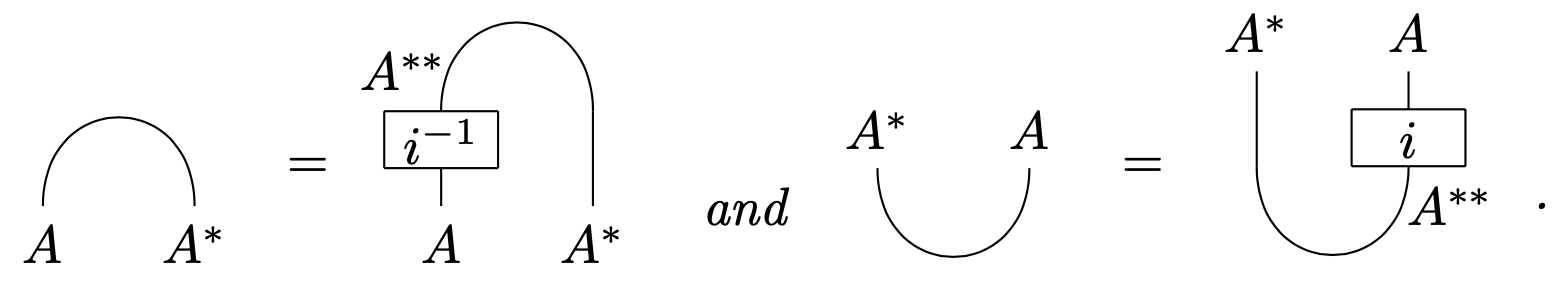
The following properties are satisfied:
- These morphisms satisfy the rigidity axioms. This is, for all
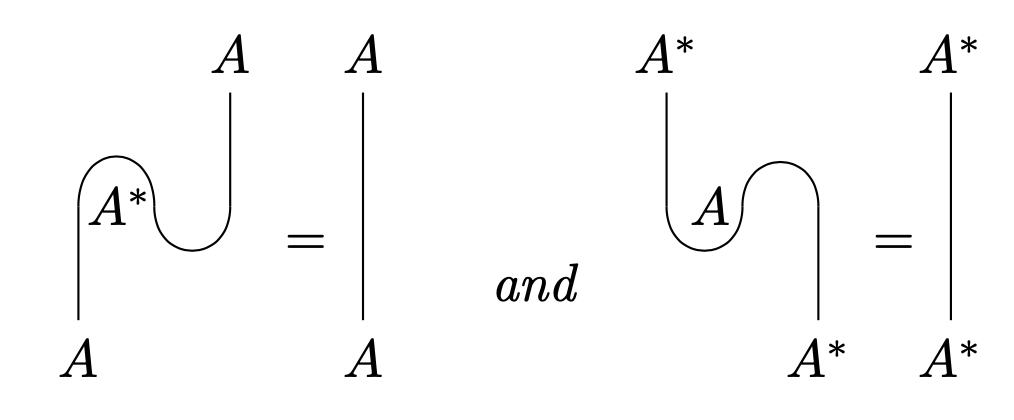
- For all ,
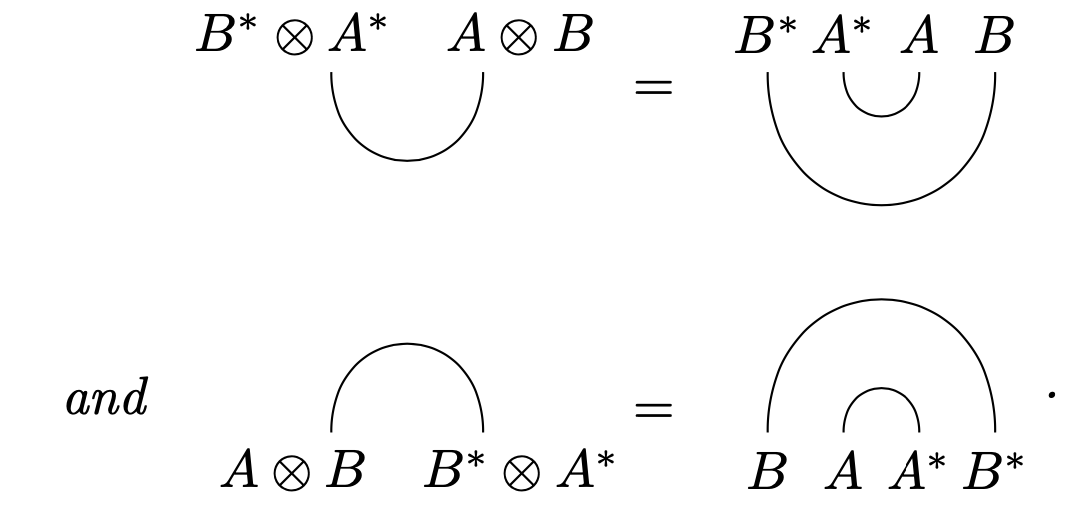
- For all , ,
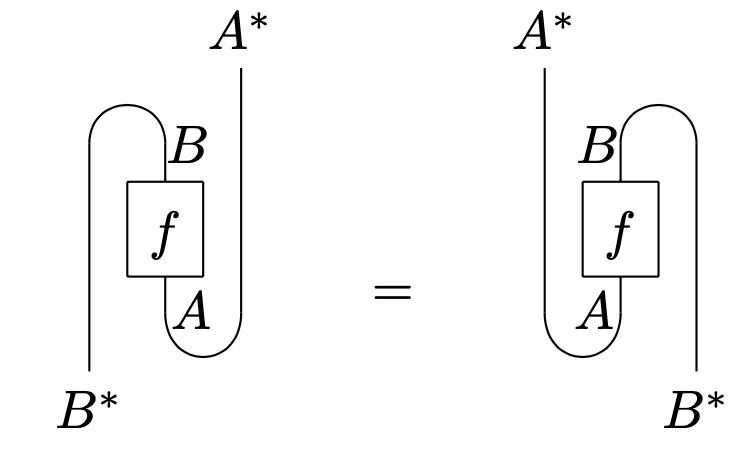
Conversely, any rigid category with duals satisfying these axioms will be pivotal under the functor

This gives a bijection between pivotal categories and rigid categories with duals satisfying these axioms.
Proof
See Bartlett Section 5.1.
In braided monoidal categories
It is a general principle that rigidity behaves much better in braided monoidal categories. For instance, every braided rigid category will automatically have two-sided duals (Joyal and Street, Proposition 7.2). However, there is no a-priori reason for a pivotal structure to exist. What is true is that pivotal structures can be quantified explicitly in terms of twists:
Proposition
[Deligne] Let be a braided rigid monoidal category. Given any natural isomorphism such that for all , the distinguished morphisms
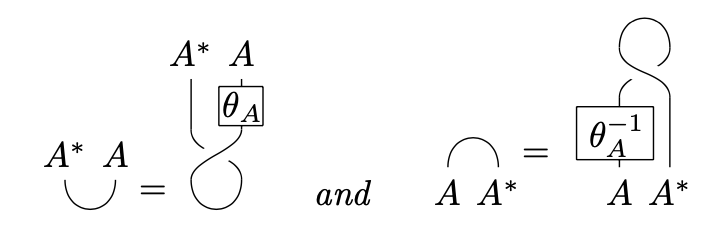
give the structure of a pivotal category. This map induces a canonical bijection between the set of pivotal structures on and the set of natural isomorphism satisfying for all .
Proof
An exposition can be found in this article of Yetter.
A braided rigid monoidal category with a twist is called balanced (not to be confused with the other unrelated notion of balanced). This result can be read as saying that a braided rigid monoidal category is balanced if and only if it is pivotal. Morally, we have the following explanation:
“The lemma is remarkable because the concept of a braided autonomous category does not include any assumption relating the braided structure to the autonomous structure. Moreover, the axioms for a twist depend only on the braided structure, whereas the axioms for a pivotal structure depend only on the autonomous structure. Yet, they are equivalent if is braided autonomous” - Peter Selinger
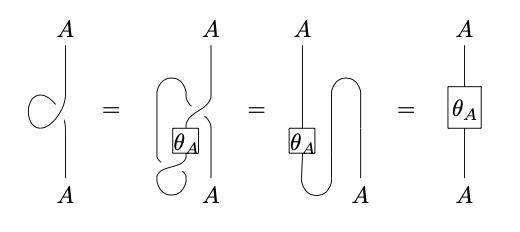
Given a pivotal structure, the twist can be recovered explicitly using graphical language as follows:
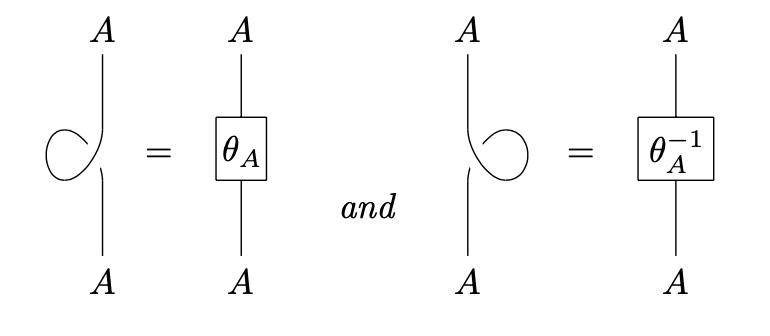
The proof of this result is a simple untangling:
In fusion categories
In every fusion category, we automatically have that every object is isomorphic to its double dual. This is because fusion categories are semisimple, so admitting a non-zero morphism into is the same as there being a in the simple object decomposition of , which in turn is the same as admitting a non-zero morphism into .
It is a deep conjecture of Etingof, Nikshych, and Ostrik that every fusion category is pivotal. This conjecture was proposed in their seminal work, On fusion categories. What one gets a-priori, however, is a natural isomorphism between every object and its quadruple dual, called the Radford isomorphism. This weaker isomorphism is already very powerful, and serves as an important tool in the theory of fusion categories.
Related concepts
-
pivotal category
References
-
Pavel Etingof, Dmitri Nikshych, Viktor Ostrik, On fusion categories, Annals of Mathematics, arXiv
-
Andre Joyal, Ross Street, Braided tensor categories, Advances in Mathematics, pdf
-
Shlomo Gelaki, Nilpotent fusion categories, Advances in Mathematics, arXiv
-
David Yetter, Framed tangles and a theorem of Deligne on braided deformations of tannakian categories, Contemporary Mathematics, web
-
Bruce Bartlett, On unitary 2-representations of finite groups and topological quantum field theory, PhD thesis, arXiv
Last revised on May 18, 2023 at 16:21:05. See the history of this page for a list of all contributions to it.