nLab Music of the Spheres
Context
Philosophy
Schools
Of mathematics
Of physics
Spheres
Stable Homotopy theory
Ingredients
Contents
Contents
Idea
Ancient idea

In ancient times, Musica Universalis or Music of the Spheres referred to a philosophical concept that regards proportions of orbits in the solar system as exhibiting a cosmic harmony (Plato 380BC).
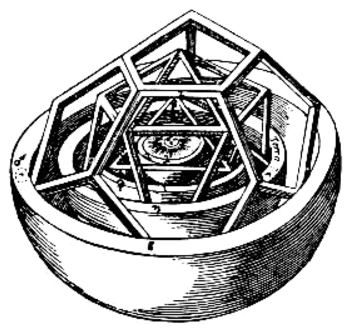
Johannes Kepler proposed that this is governed by the shape of the Platonic solids (Kepler 1596). (See also at multiverse.)
Modern idea

More recently, it was suggested that the term refers to the stable homotopy groups of spheres and the absolute E-∞ geometry over Spec(S) as seen by the MU-Adams spectral sequence.
My initial inclination was to call this book The Music of the Spheres, but I was dissuaded from doing so by my diligent publisher, who is ever mindful of the sensibilities of librarians. (Ravenel 86, p. xv)
For the last 50 years one of the basic problems in algebraic topology has been the determination of the homotopy groups of spheres (Mahowald-Ravenel 87, Sec. 1)
As is well known, it is our manifest destiny as 21st century algebraic topologists to compute homotopy groups of spheres. (Wilson 13, p. 1)
One of the most fundamental problems in topology is to determine the set of homotopy classes of continuous based maps between spheres. (Isaksen-Wang-Xu 20, Sec. 1)
Modern chromatic homotopy theory makes contact between this kind of music and physics:
-
the A-hat genus (partition function of the spinning particle) appears in the first chromatic level of the spheres;
-
the Witten genus (partition function of the spinning string) appears in the second chromatic level of the spheres.
Modern equivariant stable homotopy theory makes contact between this kind of music and Kepler’s proposal:
- the equivariance of the quaternionic Hopf fibration under the symmetry groups of the Platonic solids (icosahedral group, octahedral group, tetrahedral group) makes further equivariant stable homotopy groups of spheres appear, see at quaternionic Hopf fibration – class in equivariant stable homotopy theory.
For whatever it’s worth, all these items come together in the Equivariant cohomology of M2/M5-branes
Related concepts
References
-
Wikipedia, Musica universalis
-
Doug Ravenel, Complex cobordism and stable homotopy groups of spheres, 1986/2003
-
Mark Mahowald, Doug Ravenel, Towards a Global Understanding of the Homotopy Groups of Spheres, in: Samuel Gitler (ed.): The Lefschetz Centennial Conference: Proceedings on Algebraic Topology II, Contemporary Mathematics volume 58, AMS 1987 (pdf, pdf, ISBN:978-0-8218-5063-3)
-
Dylan Wilson, Spectral Sequences from Sequences of Spectra: Towards the Spectrum of the Category of Spectra, lecture at 2013 Pre-Talbot Seminar, March 2013 (pdf)
-
Daniel Isaksen, Guozhen Wang, Zhouli Xu, Stable homotopy groups of spheres, PNAS October 6, 2020 117 (40) 24757-2476 (arXiv:2001.04247, doi:10.1073/pnas.2012335117)
Last revised on March 3, 2021 at 06:57:30. See the history of this page for a list of all contributions to it.