Schreiber Equivariant cohomology of M2/M5-branes
Generalized cohomology of M2/M5-branes
talk at
Seminar on Higher Structures in the Program on Higher Structures in Geometry and Physics,
MPI Bonn, 15 Jan 2016
Abstract. While it is well-known that the charges of F1/Dp-branes in type II string theory need to be refined from de Rham cohomology to certain twisted generalized differential cohomology theories, it is an open problem to determine the generalized cohomology theory for M2-brane/M5-branes in 11 dimensions. I discuss how a careful re-analysis of the old brane scan (arXiv:1308.5264 , arXiv:1506.07557, joint with Fiorenza and Sati) shows that rationally and unstably, the M2/M5 brane charge is in degree-4 cohomotopy. While this does not integrate to the generalized cohomology theory called stable cohomotopy, it does integrate to -equivariant stable cohomotopy, for a non-cyclic finite group of ADE type. On general grounds, such an equivariant cohomology theory needs to be evaluated on manifolds with ADE orbifold singularities, and picks up contributions from the orbifold fixed points. Both of these statements are key in the hypothesized but open problem of gauge enhancement in M/F-theory.
Acknowledgement. This note profited from discussion with David Barnes, Domenico Fiorenza, Thomas Nikolaus, Charles Rezk, David Roberts, Hisham Sati. It is adapted from a previous talk “Generalized cohomology of M2/M5-branes” at Higher Structures in String Theory, ESI Vienna, 11 Dec 2015.
For details see:
-
John Huerta, Hisham Sati, Urs Schreiber,
Real ADE-equivariant (co)homotopy and Super M-branes
Communications in Mathematical Physics (2019)
-
Equivariant Cohomotopy implies orientifold tadpole cancellation
Contents
- Background
- -algebras and Rational homotopy theory
- Higher WZW-type sigma-models
- Green-Schwarz functionals for Super -branes
- The open problem
- Warmup: Generalized cohomology of F1/Dp-brane charges
- The rational cohomology of M2/M5-brane charges
- Lift to ADE-equivariant stable cohomotopy
- Conclusion and outlook
Background
We are going to analyze an open problem in the mathematical theory of super p-branes. Before even stating the open problem and its analysis, we do need to briefly recall what super -branes are, mathematically. Lecture notes with more details on the following are in (Schreiber 15). Full details are in (dcct).
-algebras and Rational homotopy theory
Rationally, what we are going to be concerned with is all enoced in L-∞ algebra cohomology for super L-∞ algebras. We briefly recall this, following (Sati-Schreiber-Stasheff 09). For more exposition see at super Cartan geometry. All algebras here are over .
The operation of sending finite dimensional Lie algebras to their Chevalley-Eilenberg algebras is a fully faithful functor
from the category of Lie algebras to the opposite category of dg-algebras.
Generalizing the image of this functor to those dg-algebras of the form for an -graded vector space of finite type yields the opposite of the category of (connective) L-∞ algebras of finite type:
Accordingly, super L-∞ algebras are given by generalizing this further to being an -graded super vector space of finite type and regarding the Grassmann algebra as -bigraded (see at signs in supergeometry).
The category carries a canonical homotopical structure whose weak equivalences are the quasi-isomorphisms on the underlying chain complexes (Pridham 07).
For denoting the line Lie (p+2)-algebra (whose Chevalley-Eilenberg algebra is generated in degree with vanishing differential) then an -algebra homomorphism
is equivalently a -cocycle in L-infinity algebra cohomology. Its homotopy fiber is the L-∞ algebra extension that it classifies
Proposition
For , the homotopy fiber of a cocycle is given by
(Fiorenza-Rogers-Schreiber 13, theorem 3.1.13)
Example
For a semisimple Lie algebra and the canonical 3-cocycle, its homotopy fiber is the string Lie 2-algebra.
This -extension will in general carry new cocycles, so that towers and bouquets of higher extensions emanate from any one super -algebra
This reminds one of Whitehead towers in homotopy theory. And indeed, there is Lie integration of -algebras, which connects them both to smooth ∞-groups and to rational homotopy theory:
For a Lie algebra, then the 2-coskeleton of the simplicial set
is the simplicial nerve of the simply connected Lie group corresponding to :
To remember the smooth structure on we simply parameterize this over smooth manifolds . Then the simplicial presheaf
gives the smooth stack delooping of the Lie group :
This generalizes verbatim to a Lie integration functor
from (super-)L-∞ algebras to simplicial presheaves over supermanifolds, hence (super-)smooth ∞-stacks.
(Henriques 08, Fiorenza-Schreiber-Stasheff 12).
Notice that for a Sullivan model, then over the point this is the Sullivan construction of rational homotopy theory. For instance the Eilenberg-MacLane spaces
This will be key in the following: -theory allows to derive the cohomological nature of the charges of super p-branes, but only in rational homotopy theory. The open problem to be discussed below is concerned with the ambiguity of lifting this to genuine (non-rational) homotopy theory.
Higher WZW-type sigma-models
Physics is all encoded in nonlinear functionals on moduli stacks of configurations of a physical system, called action functionals. We now review how every super -cocycle as above canonically induces an action functional called a higher WZW term. The super -branes below are then determined by exceptional examples of this general construction.
Proposition
There is a differential Lie integration functor that sends an -cocycle
to a smooth ∞-group equipped with a circle n-bundle with connection modulated by a map into the Deligne complex
such that
-
it lifts the plain Lie integration from above;
-
the curvature is , for the Maurer-Cartan form on the smooth ∞-group .
(Fiorenza-Schreiber-Stasheff 12, Fiorenza-Sati-Schreiber 13)
Proposition
For an oriented closed manifold of dimension , fiber integration in ordinary differential cohomology lifts to a morphism of smooth stacks
and the transgression of to the mapping stack is simply the composition
For this yields a functional
which in physics one regards as the “gauge interaction” action functional of a local field theory of “higher WZW sigma-model”-type, describing the propagation of a “-brane” with worldvolume in .
Example
The archetypical sigma-model for our purposes is that for the electron (a “0-brane”). On spacetime an electromagnetic field is represented by a circle group principal connection
For the abstract worldline of the electron, its electromagnetic interaction is encoded in the functional
namely the holonomy. The equations of motion that this induces by variation gives the Lorentz force exerted by the electromagnetic field on the electron.
By a fundamental phenomenon called Dirac charge quantization, the first Chern class
of is identified with the total magnetic charge in the spacetime . Put the other way around:
The action functional for the 0-brane is the transgression of the lift of the background charge to a cocycle in differential cohomology.
This is the blueprint for the -brane charges that we are considering.
Example
For an ordinary Lie algebra then is its ordinary simply-connected Lie group. For semisimple, then the differential Lie integration, prop. , of the string 3-cocycle from example is the original WZW gerbe
Its transgression, prop. , is its surface holonomy and this is the interaction term of the action functional for the WZW sigma model describing propagation of a string in , subject to the force exerted by a background “B-field charge”.
Notice that this process of differential Lie integration produces coefficients in ordinary differential cohomology whose curvatures are the (left-translation) of the -values -cocycles. Below we will find cocycles taking values in more complicated -algebras, and then the construction of a Lagrangian from them is less immediate.
Green-Schwarz functionals for Super -branes
By the above, each -cocycle in higher Lie theory defines a p-brane sigma-model. Particularly interesting will be exceptional cocycles. Such happen to appear when passing from Minkowski-Poincaré spacetime symmetry to supersymmetry:
Perturbativestring theory on geometric backgrounds is defined by the Neveu-Schwarz-Ramond model, namely by sigma-model 2d super conformal field theories (of central charge 15) on worldsheets that are super Riemann surfaces, with target spaces that are ordinary (i.e. “bosonic”) spacetime manifolds.
These worldsheet field theories are induced from action functionals, namely variants of the standard energy functional (Polyakov action) on the space of smooth functions
The central theorem of perturbative superstring theory says that the spectrum of such a 2d SCFT are the quanta of the perturbations of a higher dimensional effective supergravity field theory on target spacetime, hence transforms under supersymmetry on target spacetime.
This is the fundamental prediction of the assumption of fundamental strings: assuming 1) that the particles that run in Feynman diagrams are fundamentally strings, and demanding 2) that there are fermionic particles among these, first implies that the strings must be spinning strings (have fermions on their worldsheet), which implies that they are superstrings (worldsheet supersymmetry mixes the worldsheet bosons and fermions), which then in addition implies that their target space effective field theory is supergravity, hence that also the effective target space fields exhibit local supersymmetry.
The first step in this implications (spinning string is superstring) is straightforward, but the second step appears as a miracle from the point of view of the NSR string. It comes out this way by non-trivial computation, but is not manifest in the theory.
In order to improve on this situation, Green and Schwarz searched and found (Green-Schwarz 81, Green-Schwarz 82 Green-Schwarz 84) a suitably equivalent string action functional that would manifestly exhibit spacetime supersymmetry. This is now called the Green-Schwarz action functional.
| action functional for superstring | manifest supersymmetry |
|---|---|
| Ramond-Neveu-Schwarz string | on worldsheet |
| Green-Schwarz string | on target spacetime |
The basic idea is to pass to the evident supergeometric analogue of the bosonic string action:
Let be a closed manifold of dimension 2 – representing the abstract worldsheet of a string. Let be a pseudo-Riemannian manifold – representing a purely gravitational spacetime background. Then the action functional governing the bosonic string propagating in this spacetime is the functional
on the smooth mapping space of smooth functions , that simply assigns the proper relativistic volume of the image of the worldsheet in spacetime:
(This is the Nambu-Goto action. It is classically equivalently to the Polyakov action which is the genuine starting point for the quantum Neveu-Schwarz-Ramond string. Howver, since, as we discuss below, the Green-Schwarz action naturally generalizes to that of other -branes it is more natural to consider the Nambu-Goto form of the action here.)
When here is generalized to a superspacetime supermanifold with orthogonal structure encoded by a super-vielbein (see at super Cartan geometry for details), then the same form of the action functional still makes sense and produces a functional on the supergeometric mapping space . Moreover, by construction this action functional is invariant under the superisometry group of , hence under spacetime supersymmetry.
However, Green and Schwarz noticed that this kinetic action functional does not quite yield dynamics that is equivalent to that of the NSR string: when the equations of motion hold (“on shell”) it has more fermionic degrees of freedom than present in the NSR string. The key insight of Green and Schwarz was that one may add an extra summand to the action functional to the plain super-Nambu-Goto action, such that the resulting functional enjoys a further 1-parameter symmetry, called kappa-symmetry, and such that restricting to the -symmetric states, then the action functionals do become classically equivalent.
Moreover, they showed that in light-cone gauge the resulting quantum dynamics is equivalent to that of the NSR string, thus providing a conceptual proof for the observed local spacetime supersymmetry for backgrounds that admit two lightlike Killing vectors. (The quantization of the GS-string away from lightcone gauge however remains an open problem.)
Green-Schwarz’s extra kappa-symmetry term serves a clear purpose, but originally its geometrically meaning was mysterious. However, in (Henneaux-Mezincescu 85) it was observed (expanded on in (Rabin 87, Azcarraga-Townsend 89, Azcarraga-Izqierdo 95,chapter 8)), that the Green-Schwarz-action functional describing the string in -dimensions has a neat geometrical interpretation: it is simply the (parameterized) WZW-model for
-
target space being locally super Minkowski spacetime regarded as the coset supergroup
for a real spin representation (the “number of supersymmetries”), the corresponding super Poincaré group and its Lorentz-signature Spin subgroup;
-
WZW-term being a local potential for the the unique (up to rescaling, if it exists) -invariant group 3-cocycle on , with component locally given by the Gamma-matrices of the given Clifford algebra representation.
More in detail, just as ordinary Minkowski spacetime may be identified with the translation group with canonical basis of left invariant 1-forms given by the canonical vielbein field
where are the canonical coordinates on , so super Minkowski spacetime for some real spin representation is characterized as the supergroup whose left invariant 1-forms consitute the -bigraded differential with generators the super-vielbein
where are the canonical coordinates on , with the odd-graded elements spanning the given real Spin(d-1,1)-representation with Clifford algebra generators .
Now while ordinary Minkowski spacetime is an abelian group, reflected by the fact that its left-invariant 1-forms are all closed
the key phenomenon of supersymmetry (that two fermions pair to a bosons) means that is slightly non-abelian, reflected by the fact that the super-vielbein is not closed
This is the source of all the rich structure seen in Green-Schwarz theory.
In particular, for special combinations of spacetime dimension and number of supersymmetries the 3-form
is a non-trivial super Lie algebra cocycle on , in that and so that there is no left invariant differential form with .
This happens notably for and (heterotic string) or (type IIB superstring) and (type IIA superstring). (It also happens in some lower dimensions, where however the corresponding NSR-string develops a conformal anomaly after quantization (“non-critical strings”). This classification of cocycles is part of what has come to be known as the brane scan in superstring theory, see below.)
In this equivalent formulation, the Green-Schwarz action functional for the superstring has the following simple form:
Let be a superspacetime, hence a supermanifold equipped with a super-vielbein (super-orthogonal structure) which is locally modeled on (technically: a torsion-free super-Cartan geometry modeled on ). Write be the super differential form on which is the induced definite globalization of the cocycle over . For any contractible subspace, then the restriction of of to is exact, and hence admits a potential , i.e. such that .
Then for a 2-dimensional closed manifold, the Green-Schwarz action functional
is the function on the super-smooth space of smooth maps of supermanifolds which factor through , given by
In order to get rid of the restriction to some one needs to add global data. The need for this is at least mentioned briefly in (Witten 86, p. 261 (17 of 20)), but had otherwise been ignored in the physics literature. The general solution is to promote the local potentials to the connection on a super gerbe (Fiorenza-Sati-Schreiber 13). This is a choice of higher prequantization
Writing for the volume holonomy of a circle 2-bundle with connection , then the globally defined Green-Schwarz sigma model
is given by
This form of the Green-Schwarz action functional for the string has evident generalization to other -branes. Whenever there is a Lorentz-invariant -cocycle on , then one may ask for a higher gerbe (higher prequantum line bundle) with curvature and consider the analogous functional.
The triples (spacetime dimension, number of supersymmetries, dimension of brane) such that
is a nontrivial cocycle, hence for which there is such a Green-Schwarz action functional for -branes on may be classified and form what is called the brane scan (Achúcarro-Evans-TownsendWiltshire 87, Brandt 12-13):
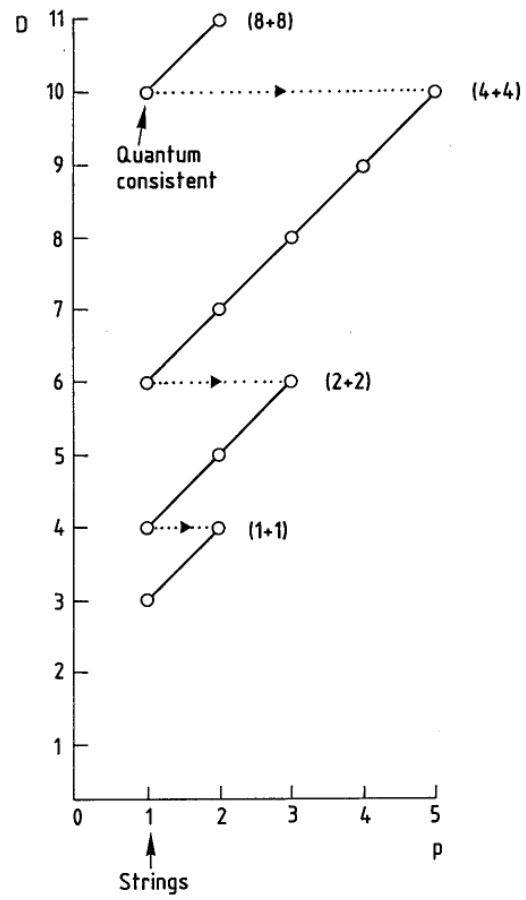
The grapics on the left is from (Duff 87). The diagonal lines indicate double dimensional reduction, taking a -brane in dimensions to a -brane in -dimensions.
For instance for one finds a cocycle, and the corresponding GS-action functional is that of the fundamental M2-brane.
This was a striking confluence of brane physics and classification of super Lie algebra cohomology. But just as striking as the matching, was what it lacked to match: the D-branes and the M5-brane (, ) are lacking from the old brane scan. Incidentally, these lacking branes are precisely those branes on which the branes that do appear on the brane scan may end, equivalently those branes that have higher gauge fields on their worldvolume (tensor multiplets).
An action functional for the M5-brane vaguely analogous to a Green-Schwarz action functional was found in (BLNPST 97, APPS 97). It is again the sum of a kinetic term and a WZW-like term, but the WZW-like term does not come from a cocycle on a (super-)group.
In order to deal with this, it was suggested in (CAIB 99, Sakaguchi 00, Azcarraga-Izquierdo 01) that there is an algebraic structure called “extended super-Minkowski spacetimes” that generalizes super Minkowski spacetime and serves to unify the Green-Schwarz-like models for the D-branes and the M5-brane with the original Green-Schwarz models for the string and the M2-brane.
These extended super-Minkowski spacetimes carry algebraic analogs of super Lie algebra cocycles, such that the relevant terms for the D-branes and the M5-brane do appear after all, hence such that all the branes in string theory/M-theory are unified. In fact these “extended super-Minkowski spacetimes” are precisely the “FDA”s that have been introduced before in the D'Auria-Fré formulation of supergravity and what became identified as the 7-cocycle for the M5-brane this way had earlier been recognized algebraically as an stepping stone for an elegant re-derivation of 11-dimensional supergravity (D’Auria-Fré 82).
The (higher) geometric meaning of these constructions was found in (Fiorenza-Sati-Schreiber 13): these algebraic structures of “extended super-Minkowski spacetimes”/FDAs are precisely the Chevalley-Eilenberg algebras of super Lie n-algebra-extensions of super-Minkowski spacetime which are classified by the cocycles that serve as the GS-WZW terms of the -branes that may end on those -branes whose cocycles are carried by the extended super-Minkowski spacetime.
Hence the missing -branes in the old brane scan (classifying just cocycles on super Lie algebras) do appear as one generalizes (super) Lie algebras to (super) strong homotopy Lie algebras = L-infinity algebras. Moreover, each brane intersection law (one brane species may end on another) is now matched to a super -algebra extension and so the old brane scan is generalized to a tree of branes The brane bouquet:
Each item in this bouquet denotes a super L-infinity algebra and each arrow denotes an L-infinity extension classified by a cocycle which encodes the GS-WZW term of the brane named by the domain of the arrow.
In (Fiorenza-Sati-Schreiber 13) it is shown that all these super L-infinity algebras Lie integrate to smooth super-n-groups, and all the cocycles Lie integrate to super-gerbes on these, such that the induced volume holonomy is the relevant generalized GS-WZW term. For detailed exposition see at Structure Theory for Higher WZW Terms.
With this generalized perspective, now the Green-Schwarz-type action functionals describe all the p-branes in string theory/M-theory.
Again, in order to make this generally true one needs to apply a higher prequantization – a choice of line (p+1)-bundle with connection – in order to globalize the WZW-terms (Fiorenza-Sati-Schreiber 13)
Hence is the actual background field that the -brane couples to. There is considerably more information in than in its curvature . For instance for the M2-brane one may find the local super moduli space for local choices of for the given on KK-compactifications to . It turns out that the bosonic body of this moduli space is the exceptional tangent bundle on which the U-duality group E7 has a canonical action (see at From higher to exceptional geometry).
This highlights that Green-Schwarz functionals capture fundamental (“microscopic”) aspects of -branes. In contrast, often -branes are discussed in their solitonic incarnation as black branes. These solitonic branes sit at asymptotic boundaries of anti-de Sitter spacetime and carry conformal field theories, related to the ambient supergravity by AdS-CFT duality.
This phenomenon is indeed a consequence of the fundamental Green-Schwarz branes:
Consider a 1/2-BPS state solution of type II supergravity or 11-dimensional supergravity, respectively. These solutions locally happen to have the same classification as the Green-Schwarz branes. Hence we may consider a configuration of the corresponding fundamental -brane which embeds into the asymptotic AdS boundary of the given 1/2 BPS spacetime . Then it turns out that restricting the Green-Schwarz action functional to small fluctuations around this configuration, and applying a diffeomorphism gauge fixing, then the resulting action functional is that of a supersymmetric conformal field theory on as in the AdS-CFT dictionary:
| fundamental -brane | -fluctuations about asymptotic AdS configuration | solitonic -brane |
|---|---|---|
| Green-Schwarz action functional | super-conformal field theory |
(Claus-Kallosh-Proeyen 97, Claus-Kallosh-Kumar-Townsend 98, AFFFTT 98 Pasti-Sorokin-Tonin 99).
In fact the BPS-state condition itself is neatly encoded in the Green-Schwarz action functionals: by construction they are invariant under the spacetime superisometry group. Hence the Noether theorem implies that there are corresponding conserved currents, whose Dickey bracket forms a super-Lie algebra extension of the Lie algebra of supersymmetries.
Here the “” filling the triangles is the non-trivial gauge transformation by which the WZW term (as any WZW term) is preserved under the symmetries (instead of being fixed identically). It is the information in this transformations which makes the currents form an extension of the symmetries.
Here this yields the famous brane charge extensions of the super-isometry super Lie algebra of the schematic form
(for a Killing spinor and its corresponding Killing vector) known as the type II supersymmetry algebra and the M-theory supersymmetry algebra, respectively (Azcárraga-Gauntlett-Izquierdo-Townsend 89). In fact it yields super-Lie n-algebra extensions of which the familiar super Lie algebra extensions are the 0-truncation (Sati-Schreiber 15, Khavkine-Schreiber 16).
In summary, the nature and classification of Green-Schwarz action functionals captures in a mathematically precise way a good deal of the core structure of string/M-theory.
In fact, the super L-infinity algebraic perspective on the Green-Schwarz functionals via The brane bouquet also solves the following open problem on M-branes:
it is famously known from Freed-Witten anomaly-cancellation that the D-brane charges are not in fact just in de Rham cohomology in every second degree, but are in twisted K-theory, hence rationally in twisted de Rham cohomology, with the twist being the F1-brane charge (from the fundamental). It is an open problem to determine what becomes of these twisted K-theory charge groups as one lifts F1/D-branes in string theory to M2/M5-branes in M-theory.
| intersecting branes | charges in generalized cohomology theory | |
|---|---|---|
| string theory | F1/Dp-branes | twisted K-theory |
| M-theory | M2/M5-branes | ??? |
Notice that there are “microscopic degrees of freedom” of the theory encoded by the choice of generalized cohomology theory here, generalizing the extra degrees of freedom in the choice of a WZW-term already mentioned above. In general for a cohomology theory and its Chern character map (for instance from topological K-theory to ordinary cohomology in every second degree), then a choice of genuine charges is the extra information encoded in a lift
But rationally The brane bouquet allows to derive this from first principles:
Above we saw that the naive cocycles of the D-branes and of the M5-brane are not defined on the actual spacetime, but on some “extended” spacetime, which is really a smooth super infinity-groupoid extension of spacetime. Hence we should ask if these cocycles descend to the actual super-spacetime while picking up some twists.
One may prove that:
-
the F1/D-brane GS-WZW cocycles descend to 10d type II superspacetime to form a single cocycle in rational twisted K-theory, just as the traditional lore reqires (Fiorenza-Sati-Schreiber 16);
-
the M2/M5 GS-WZW cocycles descent to 11d superspacetime to form a single cocycle with values in the rational 4-sphere (Fiorenza-Sati-Schreiber 16).
This we turn to now.
The open problem
We are now ready to state the open problem to be analyzed. We first give its purely mathematical content.
Twisted generalized cohomology from prescribed rationalization
Given one stage in the brane bouqet
then is a -principal ∞-bundle over .
This and the following statements all are the general theorems of (Nikolaus-Schreiber-Stevenson 12) specified to -algebras regarded as infinitesimal -stacks (aka “formal moduli problems”) according to dcct.
Hence it is natural to ask whether the second cocycle , defined on the total space (stack) of this bundle is equivariant under the ∞-action of . If does not itself already come from the base space, then it can at best be equivariant with respect to an -∞-action on .
First, specifying such ∞-action is equivalent to specifying a second homotopy fiber sequence of the form as on the right of this completed diagram:
Second, given , then the -equivariance of is equivalent to it descending down the homotopy fibers on both sides to an -homomorphism of the form
making this diagram commute in the homotopy category:
In conclusion:
Remark
The resulting triangle diagram
regarded as a morphism
in the slice over exhibits as a cocycle in (rational) -twisted cohomology with respect to the local coefficient bundle .
(Nikolaus-Schreiber-Stevenson 12)
Notice that a priori this is (twisted) nonabelian cohomology, though it may happen to land in abelian-, i.e. stable-cohomology.
Such descent is what one needs to find for The brane bouquet above, in order to interpret each of its branches as encoding -brane model on spacetime itself. This is a purely algebraic problem which has been solved (Fiorenza-Sati-Schreiber 15). We discuss the solution in a moment.
But then the open problem is this: now the new rational coefficients is (in the slice over ). This is no longer of the simple abelian form for which there exists the differential Lie integration functro from above. So:
Open problem: Find twisted differential cohomology theories which lifts the rational situation of remark through its Chern character map. In particular its curvature forms are to be in .
To illustrate this problem in a situation where the solution is something well-known, we first discuss below how to derive from super -cohomology the famous statement that F1/Dp-brane charges are in twisted K-theory.
Then further below we finally turn to the analogous but open case of M2/M5-brane charges.
M-brane charges
Here is a comment on the significance of the above for physics. This is not needed for the mathematical discussion below, but it may help to motivate it.
Inspection shows that what is known for sure about M-theory (Witten 95) is all encoded in the prequantum Green-Schwarz-type sigma-models describing the propagation of M2-branes and M5-branes on super-spacetimes. In particular:
-
The BPS charges of such spacetimes – which are traditionally argued to probe properties of the full quantum regime of the elusive theory – are identified with the charges of the Noether currents of these sigma-models.
In fact the Heisenberg Lie n-algebra (Fiorenza-Rogers-Schreiber 13) of these prequantum field theories is The M-Theory BPS charge super Lie 6-algebra, whose 0-truncation is the M-theory super Lie algebra “” (Sati-Schreiber 15, Schreiber-Khavkine 16).
-
The membrane instanton contributions – which are argued to detect further non-perturbative effects – are the volume holonomy, i.e. the magnetic flux, of the complexified higher WZW term of the M2-brane over supersymmetric cycles (Schreiber 15).
-
The definite globalization of the M2-WZW term over a superspacetime implies the equations of motion of 11-dimensional supergravity (hence in particular the Hodge duality between the rational M-brane charges) together with the classical anomaly cancellation that makes the M2-sigma model be globally well defined on this target (Schreiber 15).
Moreover:
- The conformal field theories in the near-horizon limit of M2/M5-black brane configurations (as in AdS4/CFT3 and AdS7-CFT6) arise as the small fluctuations of the Green-Schwarz sigma-models around classical M-brane configurations embedded into the asymptotic AdS-boundary (Claus-Kallosh-Proeyen 97,Dall’Agata-Fabri-Fraser-Fré-Termonia-Trigiante 98, Claus-Kallosh-Kumar-Townsend 98, Pasti-Sorokin-Tonin 99). (This is for the abelian case of single branes, we get to the all-important nonabelian case below).
Therefore, for making progress with the open question of formulating M-theory proper, a key issue is a precise understanding of the cohomological nature of M-brane charges (Sati 10) as twisted differential cohomology along the lines above.
In most of the existing literature, these charges are being regarded in de Rham cohomology. But it is well known (see (Distler-Freed-Moore 09) for the state of the art) that in the small coupling limit where the perturbation theory of type II string theory applies, the brane charges are not just in (twisted, self-dual) de Rham cohomology, but instead in a (twisted, self-dual) equivariant generalized cohomology theory, namely in real (-equivariant) topological K-theory, of which de Rham cohomology is only the rational shadow under the Chern character map. This makes a crucial difference (Maldacena-Moore-Seiberg 01, Evslin-Sati 06): the differentials in the Atiyah-Hirzebruch spectral sequence for K-theory describe how de Rham cohomology classes receive corrections as they are lifted to K-theory: some charges may disappear, others may appear.
But the lift of this situation to M-branes had been missing. The open question is: Which equivariant generalized cohomology theory do M-brane charges take values in?
The answer needs to satisfy (at least) the following two consistency conditions:
-
the rationalization of the generalized cohomology classes has to reproduce the correct rational brane charges, we analyze these below in The rational cohomology of M2/M5-brane charges;
-
the -equivariant Atiyah-Hirzebruch spectral sequence for along an M-theory circle fibration
needs to be a suitable higher order correction to the AHSS for topological KR-theory .
Here we are concerned with the first item. By the analysis in (Sati-Varghese 03, section 4), at the rational level the second item is implied by the first, see the conclusion below.
Warmup: Generalized cohomology of F1/Dp-brane charges
To illustrate the general approach, we give a re-derivation from super -cohomology of the famous identification of F1/D-brane charges in twisted K-theory (Fiorenza-Sati-Schreiber 16).
The super Minkowski spacetime – locally modeling super spacetimes in 10d type IIA supergravity – carries super -extensions of the following form (FSS 13):
Here the homotopy fiber is the -principal ∞-bundle classified by the 3-cocycle for the F1-brane (the type IIA superstring), just like the string Lie 2-algebra-extension of example , but now for the super-part of the symmetry group. Therefore this has sometimes been called the “superstring super Lie 2-algebra”.
By the above (Nikolaus-Schreiber-Stevenson 12), asking whether the cocycles for the D-branes are -equivariant and descend as twisted cocycles down to super-Minkowski spacetime is equivalent to asking whether there is a homotopy fiber sequence and a homotopy-commuting diagram of the form
Inspection shows that this indeed exists: write for the L-∞ algebra whose Chevalley-Eilenberg algebra has generators and in the indicated degrees, with non-trivial differential given by :
Moreover write for the super -algebra whose Chevalley-Eilenberg algebra is that of with generators and added, subject to . This is a resolution
of type IIA super-Minkowski spacetime which serves to represent morphisms in the homotopy theory for super L-infinity algebras in the following. Because with this, the above descent problem indeed has a solution as follows:
This says that the type IIA F1-brane and D-brane cocycles with -coefficients do descent to super-Minkowski spacetime as one single cocycle with coefficients in the homotopy quotient .
But these rational coefficients are precisely the rational image of twisted topological K-theory.
Accordingly, the Lie integration of this rational situation to twisted K-theory, and its globalization over a 10-dimensional IIA super spacetime , yields a diagram of parameterized spectra in smooth infinity-stacks of the form
According to (Sati-Schreiber-Stasheff 09, Nikolaus-Schreiber-Stevenson 12) here the morphism denoted represents the Kalb-Ramond B-field under which the F1-brane is charged and the morphism denoted represents the RR-field under which the D-branes are charged.
This is how one may re-discover the familiar cohomological nature of the F1/Dp-brane charges in type II string theory from an analysis of the super -cohomology embodied in the brane bouquet-refinement of the old brane scan.
The rational cohomology of M2/M5-brane charges
We now consider the analogue of this re-derivation, but up in 11-dimensions, where it provides a previously missing derivation of the rational cohomology of M-brane charges.
For the 11-dimensional super Minkowski spacetime on which 11-dimensional supergravity is locally modeled (via super Cartan geometry) the iterative extension of -cocycles in the brane bouquet looks like so (Fiorenza-Sati-Schreiber 13):
Hence the M5-brane WZW term exists on the -principal infinity-bundle that is classified by the M2-brane WZW term. Again using (Nikolaus-Schreiber-Stevenson 12), we may ask if this is equivariant and descends back to 11-dimensional super-Minkowski spacetime.
And it does (Fiorenza-Sati-Schreiber 15):
write for the L-infinity algebra whose Chevalley-Eilenberg algebra is generated from elements and , in degrees 4 and 7 as indicated, and whose differential is given by and . This sits in a homotopy fiber sequence of L-infinity algebras of the form
Notice that if we think of the Chevalley-Eilenberg algebras of these -algebras as being Sullivan models in rational homotopy theory, then this homotopy fiber sequence is the rational image of the quaternionic Hopf fibration
Now computation shows (Fiorenza-Sati-Schreiber 15) that indeed the WZW term for the M5-brane does descend back to super-Minkowski spacetime as a cocycle with coefficients in this rational 4-sphere:
Hence we read off from this computation that, rationally, M2-brane charge is in degree-4 ordinary cohomology and it twists M5-brane charge which is, rationally, in unstable degree-4 cohomotopy. This confirms a statement made earlier in (Sati 10, section 6.3, Sati 13, section 2.5).
An unstable Lie integration of this situation, in direct analogy to the above situation for twisted K-theory, would be given by maps into the quaternionic Hopf fibration
where the left map would represent the magnetic M2-brane charge and the horizontal map the -twisted magnetic M5-brane charge. (Here we are displaying a diagram of smooth infinity-stacks, there is a further refinement of these cocycles to nonabelian differential cohomology (FSS 15)).
Notice that, unstably, the 4-sphere is just the space whose non-torsion homotopy groups (hence those that are visible rationally) are in degrees 4 and 7
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 |
Hence, unstably, the 4-sphere may be thought of as the coefficient which is just right for detecting integral M2-brane charge and M5-brane charge. For instance the near-horizon limit of a black M2-brane is the spacetime and the degree-4 cohomotopy classes
detect the integral charge of these (the M2 being the magnetic source for M5-brane charge), with the unit of charge being represented by the quaternionic Hopf fibration. Similarly the near-horizon limit of a black M5-brane is and again the degree-4 cohomotopy classes are
detecting the integral charge of these branes.
But unstable cohomotopy – which may be thought of as a very nonabelian cohomology theory – is unlikely to satisfy consistency condition 2 of reproducing topological K-theory in a suitable limit, for that we need an actual “abelian” cohomology theory represented by a spectrum. This we turn to now.
Lift to ADE-equivariant stable cohomotopy
It follows that the first of our two consistency conditions is to be solved by finding a (possibly equivariant) generalized cohomology theory whose rational image is 4-shifted cohomotopy.
The immediate guess might be that this is 4-shifted stable cohomotopy, i.e. the generalized cohomology theory which is represented by the suspension spectrum of the 4-sphere, hence by the 4-suspended sphere spectrum :
However, this does not work: the non-torsion element in , which is the one represented by the quaternionic Hopf fibration, becomes torsion after stabilization – since the third stable homotopy group of spheres is the cyclic group – and hence disappears rationally:
A natural way to evade this problem is to ask for a finite group acting on the quaternionic Hopf fibration and to consider -equivariant stable cohomotopy. Since this forces all homotopies to exist -equivariantly, it potentially makes some unstable non-torsion elements remain stably non-torsion.
More concretely, there is “genuine” -equivariant cohomology theory, motivated as follows. The traditional suspension isomorphism
relates the integer grading of cohomology groups with -fold suspensions of base spaces given by smash product with the -sphere. In a context where all spaces and coefficients are equipped with -action, then one may consider not just plain spheres but representation spheres given by one-point compactification of linear -representations . The usual spheres are subsumed by this as coming from the trivial representations: . This gives rise to a generalized grading of cohomology groups not just by integers, but by linear -representations – called RO(G)-grading – such that an equivariant suspension isomorphism holds
for any linear -representations and .
An equivariant version of the Brown representability theorem states that every RO(G)-graded equivariant cohomology theory is represented by what is called a genuine G-spectrum. Where an ordinary spectrum is a system of pointed topological spaces indexed by the integers, hence by the ordinary spheres , and equipped with compatible comparison maps
a genuine G-spectrum is a system of pointed topological spaces indexed by representation spheres and equipped with compatible comparison maps of the form
In particular for any pointed topological G-space, there is the corresponding -equivariant suspension spectrum whose value on a representation sphere is the smash product .
Hence the problem that is torsion may potentially be fixed by finding a finite group and a -action on the quaternionic Hopf fibration, , such that is a representation sphere for a 7-dimensional linear -representation, and such that the -equivariant quaternonic Hopf fibration represents a non-torsion element in
Now, by the way the quaternionic Hopf fibration is obtained, via the Hopf construction, from the product operation on the quaternions , it is equivariant under the induced action of the automorphism group of the quaternions. This automorphism group is the special orthogonal group , acting on the imaginary quaternions by rotation:
Since we need equivariance under a finite group, our options are finite subgroups of
These finite subgroups have an ADE classification. In the A-series they are the cyclic groups, sitting in the inclusion . In the D-series these are the dihedral groups which are those subgroups generated from a cyclic subgroup rotating in some plane and a reflection at that plane. Finally there are three exceptional finite subgroups: the tetrahedral group, the octahedral group and the icosahedral group
Regard both and as pointed topological G-spaces via the -action induced via automorphisms of the quaternions. Write
for the corresponding equivariant suspension spectra.
Remark
The 4-sphere with this action is manifestly a representation sphere
We will write for this representation sphere.
Moreover, the 7-sphere with this action is also a representation sphere, via stereographic projection
We will write for this.
Recall again that if we took trivial , then in the stable homotopy category
Theorem

Let be a non-cyclic finite subgroup, hence a dihedral group or one of the three exceptionals: the tetrahedral group, the octahedral group, the icosahedral group.
Then in -equivariant homotopy theory the quaternionic Hopf fibration represents a non-torsion group, i.e.
with the quaternionic Hopf fibration, regarded as a -equivariant map, representing the element .
Proof
First use the Greenlees-May decomposition which says that for any two -equivariant spectra and writing for their equivariant homotopy groups, organized as Mackey functors for all subgroups , then the canonical map
is rationally an isomorphism.
With this we are reduced to showing that there exists and a morphism of Mackey functors of equivariant homotopy groups which is not a torsion element in the abelian hom-group of Mackey functors.
To analyse this, we use the tom Dieck splitting which says that the equivariant homotopy groups of equivariant suspension spectra contain a direct summand which is simply the ordinary stable homotopy groups of the naive fixed point space :
(here denotes the Weyl group, the quotient group of the normalizer subgroup (of in ) by ).
Now observe that the fixed points of the -action on the quaternionic Hopf fibration that we are considering is just the real Hopf fibration:
since acts transitively on the imaginary quaternions and fixes the real quaternions. By our assumption that does not come through it follows that this statment is still true for :
But the real Hopf fibration represents the non-torsion element .
In conclusion then, at and we find that the -equivariant quaternionic Hopf fibration contributes a non-torsion element in
which appears as a non-torsion element in
and hence in .
Conclusion and outlook
In conclusion, a consistent possibility for the equivariant generalized cohomology theory in which M2/M5-brane charges take value is 4-shifted DE-equivariant stable cohomotopy in RO(G)-degree
(in the notation of remark ), hence the cohomology theory
The ADE-equivariance (or rather: DE-equivariance) which we discovered this way from the mathematics is a pleasant surprise:
The key conjecture (Sen 97) on the nature of the elusive “microscopic degrees of freedom” of M-theory states (see Acharya-Gukov 04 for review) that
-
its spacetimes are ADE orbifolds;
-
the theory is non-degenerate – in that it exhibits the nonabelian gauge enhancement – only at the ADE singularities, i.e. at the fixed points of the ADE-action.
This comes form the following physical heuristics (Sen 97):
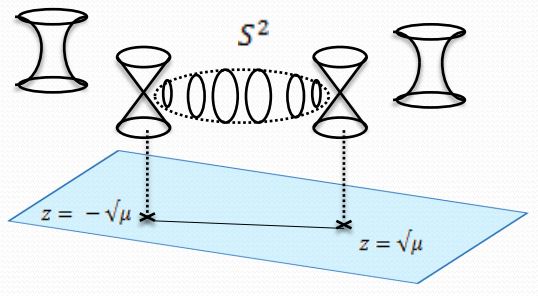
The de-singularization of an ADE singularity via blow-up is a system of touching spheres forming the corresponding Dynkin diagram. Under double dimensional reduction the M2-brane wrapped on this configuration becomes the type IIA string stretched between non-coincident D6-branes in the form of the Dynkin diagram. Here type IIA string theory applies and yields that the quiver gauge theory on these D-branes exhibits gauge enhancement to the corresponding ADE-simple gauge group as the D-branes are brought together again. But this end result must be the same as applying double dimensional reduction to the original ADE-singular M-theory configuration. Hence there must be nonabelian ADE-simple gauge group degrees of freedom hidden in M-theory on ADE-orbifolds, waiting to be mathematically identified.
Now observe that both items above follow at least qualitatively from our mathematical analysis:
-
a -equivariant cohomology theory is to be evaluated on topological G-spaces;
-
it picks up its contributions from the fixed points – by the tom Dieck splitting principle (as in the proof of theorem ) .
This gauge enhancement in M-theory at these fixed points is to be the M-theory lift of the familiar appearance of Chan-Paton gauge fields with nonabelian structure group on coincident D-branes. But mathematically the Chan-Paton gauge fields are just elements in the twisted topological K-theory in which the D-brane charges take values, as above. Hence it seems that in order to mathematically exhibit the conjectured gauge enhancement in M-theory at ADE-singularities, it is now sufficient to show that DE-equivariant stable cohomotopy on an 11-dimensional circle fibration reduces to twisted K-theory on the 10-dimensional base. But that is just the second consistency check already mentioned at the beginning.
To check this, one may run the Serre spectral sequence/Atiyah-Hirzebruch spectral sequence for -equivariant stable cohomotopy theory on circle fibrations
We may check this rationally: By Greenlees-May decomposition our equivariant cohomology theory rationally decomposes as a direct sum of equivariant Eilenberg-MacLane spectra on the equivariant homotopy group Mackey functors
and for each of the EM-summands there is a Serre-Atiyah-Hirzebruch spectral sequence (Kronholm 10, theorem 3.1)
But by the above analysis the -page here rationally reduces to the Gysin sequence analysis in (Sati-Varghese 03, section 4).
For instance for there is the following contribution that gives the correct double dimensional reduction of the charge seen by the M5-brane to the charge seen by the D4-brane, rationally:
Here in the second step we unraveled the definition of cohomology with values in a Mackey for the case of the domain being a sphere, in the third step we used stability of the stable equivariant homotopy groups and in the fourth we used the proof of theorem .
References
-
Domenico Fiorenza, Chris Rogers, Urs Schreiber, L-∞ algebras of local observables from higher prequantum bundles, Homology, Homotopy and Applications, Volume 16 (2014) Number 2, p. 107 ? 142 (arXiv:1304.6292)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Extended higher cup-product Chern-Simons theories, Journal of Geometry and Physics, Volume 74, 2013 (arXiv:1207.5449)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields, International Journal of Geometric Methods in Modern Physics, Volume 12, Issue 02 (2015) 1550018 (arXiv:1308.5264)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, The WZW term of the M5-brane, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory and type IIA string theory 2016
-
Domenico Fiorenza, Urs Schreiber, Jim Stasheff Cech Cocycles for Differential characteristic Classes, Advances in Theoretical and Mathematical Physics, Volume 16 Issue 1 (2012) (arXiv:1011.4735)
-
Thomas Nikolaus, Urs Schreiber, Danny Stevenson, Principal ∞-bundles – General theory, Journal of Homotopy and Related Structures, Volume 10, Issue 4 (2015), pages 749-801 (arXiv:1207.0248)
-
Hisham Sati, Geometric and topological structures related to M-branes, part I, Proc. Symp. Pure Math. 81 (2010), 181-236 (arXiv:1001.5020)
-
Hisham Sati, Framed M-branes, corners, and topological invariants, (arXiv:1310.1060)
-
Hisham Sati, Urs Schreiber, Lie n-algebras of BPS charges (arXiv:1507.08692)
-
Hisham Sati, Urs Schreiber, Jim Stasheff, Twisted Differential String and Fivebrane Structures, Communications in Mathematical Physics, Volume 315, Issue 1, pp 169-213 (arXiv:0910.4001)
-
Hisham Sati, Mathai Varghese, Some Relations between Twisted K-theory and Gauge Theory, JHEP0403:016,2004 (arXiv:hep-th/0312033)
-
Urs Schreiber, differential cohomology in a cohesive topos v2 (pdf)
-
Urs Schreiber, Structure Theory for Higher WZW Terms, lecture course at Hisham Sati (org.) Flavors of Cohomology, Pittsburgh June 3-5, 2015
-
Urs Schreiber, Igor Khavkine, Lie n-algebras of higher Noether currents
-
The proof of theorem profited crucially from Charles Rezk, who suggested here that the reduction to fixed points will make the real Hopf fibration give a non-torsion contribution; and from David Barnes who amplified the use of the Greenless-May decomposition theorem. ↩
Last revised on January 23, 2020 at 11:41:14. See the history of this page for a list of all contributions to it.