nLab 6-sphere

Idea

The n-sphere of dimension $n = 6$.

Properties

Coset structure

The 6-sphere, as a smooth manifold is diffeomorphic to the coset space

$$S^6 \simeq G_2/ SU(3)$$

of G₂ (automorphism group of the octonions) by SU(3) (Fukami-Ishihara 55).

For more see at G₂/SU(3) is the 6-sphere.

The induced action of G₂ on $S^6$ induces an almost Hermitian structure which makes it a nearly Kaehler manifold?.

Review in is in Agrikola-Borowka-Friedrich 17

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

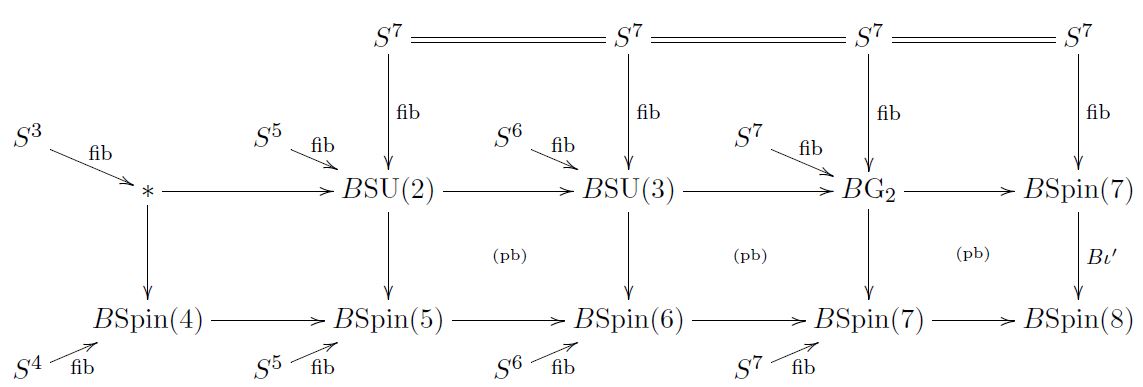
(from FSS 19, 3.4)

Complex structure

A famous open problem is the question whether the 6-sphere admits an actual complex structure. For review see Bryant 14.

Related entries

• fuzzy 6-sphere

• 2-sphere

• 3-sphere

• 4-sphere

• 7-sphere

• n-sphere

References

• T. Fukami, S. Ishihara, Almost Hermitian structure on $S^6$ , Tohoku Math J. 7 (1955), 151–156.

• Ilka Agricola, Aleksandra Borówka, Thomas Friedrich, $S^6$ and the geometry of nearly Kähler 6-manifolds (arXiv:1707.08591)

• Robert Bryant, S.-S. Chern’s study of almost-complex structures on the six-sphere (arXiv:1405.3405)

• Robert Bryant, Remarks on the geometry of almost complex 6-manifolds (arXiv:math/0508428)