nLab quaternionic Hopf fibration

Idea

The quaternionic Hopf fibration is the Hopf fibration induced by the quaternions, hence it is the fibration

$$\array{ S^3 &\hookrightarrow& S^7 \\ && \Big\downarrow^{\mathrlap{p_{\mathbb{H}}}} \\ && S^4 }$$

of the 7-sphere over the 4-sphere with fiber the 3-sphere, which is induced via the Hopf construction from the product operation

$$\mathbb{H} \times \mathbb{H} \stackrel{(-)\cdot (-)}{\longrightarrow} \mathbb{H}$$

on the quaternions, or else from

$$\mathbb{H} \times \mathbb{H}^{\times} \stackrel{(-)\cdot (-)^{-1}}{\longrightarrow} \mathbb{H}$$

to match standard conventions.

This means that if $S^7$ is regarded as the unit sphere $\{(x,y) | {\vert x\vert}^2 + {\vert y\vert}^2 = 1\}$ in $\mathbb{H}\times \mathbb{H}$ and $S^4$ is regarded as the quaternionic projective space, then $p$ is given (on points $(x,y)$ with $y \neq 0$) simply by

$$p_{\mathbb{H}} \colon (x,y) \mapsto [x;y] = [x/y; 1] \,,$$

Properties

$SO(3)$- and $Spin(5)$-Equivariant structure

Since the automorphism group of the quaternions, as an $\mathbb{R}$-algebra, is the special orthogonal group $SO(3)$

$$\mathrm{Aut}_{\mathbb{R}}(\mathbb{H}) \simeq SO(3)$$

acting by rotation of the imaginary quaternions, via the Hopf construction it follows that the 7-sphere and 4-sphere inherit $SO(3)$-actions under which the quaternionic Hopf map is equivariant.

Notice that this means that $SO(3)$ acts on $S^7$ here diagonally on the two copies of the imaginary octonions in $S^7 \hookrightarrow \mathbb{H} \oplus \mathbb{H}$ (as opposed to, say, via any one of the embeddings $SO(3) \hookrightarrow SO(8)$ and the following canonical action of $SO(8)$ on $S^7 \hookrightarrow \mathbb{R}^8$).

(see also Cook-Crabb 93)

But in fact more is true:

Proposition

(Spin(5)-equivariance of quaternionic Hopf fibration)

Consider

1. the Spin(5)-action on the 4-sphere $S^4$ which is induced by the defining action on $\mathbb{R}^5$ under the identification $S^4 \simeq S(\mathbb{R}^5)$;

2. the Spin(5)-action on the 7-sphere $S^7$ which is induced under the exceptional isomorphism $Spin(5) \simeq Sp(2) = U(2,\mathbb{H})$ (this Prop. ) by the canonical left action of $U(2,\mathbb{H})$ on $\mathbb{H}^2$ via $S^7 \simeq S(\mathbb{H}^2)$.

Then the quaternionic Hopf fibration $S^7 \overset{h_{\mathbb{H}}}{\longrightarrow} S^4$ is equivariant with respect to these actions.

This appears as (Gluck, Warner & Ziller (1986), Prop. 4.1).

The statement is also almost explicit in Porteous 95, p. 263

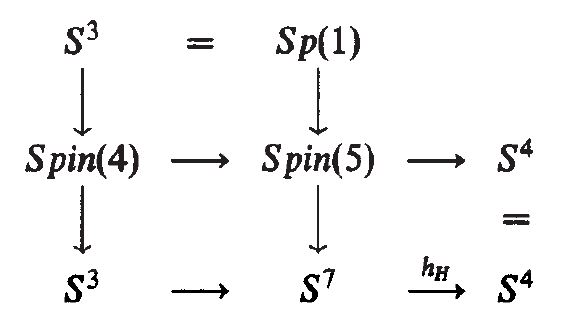
A way to make the $Spin(5)$-equivariance of the quaternionic Hopf fibration fully explicit is to observe that the quaternionic Hopf fibration is equivalently the following map of coset spaces:

$$\array{ S^3 &\overset{fib(h_{\mathbb{H}})}{\longrightarrow}& S^{7} &\overset{h_{\mathbb{H}}}{\longrightarrow}& S^4 \\ = && = && = \\ \frac{Spin(4)}{Spin(3)} &\longrightarrow& \frac{Spin(5)}{Spin(3)} &\longrightarrow& \frac{Spin(5)}{Spin(4)} }$$

(Hasuda-Tomizawa 09, table 1)

Remark

Of the resulting action of Sp(2)$\times$Sp(1) on the 7-sphere (from Prop. ), only the quotient group Sp(2).Sp(1) acts effectively.

Class in the homotopy groups of spheres

The quaternionic Hopf fibration gives an element in the 7th homotopy group of the 4-sphere

$$[p_{\mathbb{H}}] \in \pi_7(S^4) \simeq \mathbb{Z} \times (\mathbb{Z}/12)$$

and in fact it is a generator of the non-torsion factor in this group.

Stably, i.e. as a generator for the stable homotopy groups of spheres in degree $7-4 = 3$, the quaternionic Hopf map becomes a torsion generator:

$$[p_{\mathbb{H}}] \in \pi_3^S \simeq \mathbb{Z}/24 \,,.$$

The third stable homotopy group of spheres (the third stable stem) is the cyclic group of order 24:

$$\array{ \pi_3^s &\simeq& \mathbb{Z}/24 \\ [h_{\mathbb{H}}] &\leftrightarrow& [1] }$$

where the generator $[1] \in \mathbb{Z}/24$ is represented by the quaternionic Hopf fibration $S^7 \overset{h_{\mathbb{H}}}{\longrightarrow} S^4$.

Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring $\Omega^{fr}_\bullet$ of stably framed manifolds (see at MFr), this generator is represented by the 3-sphere (with its left-invariant framing induced from the identification with the Lie group SU(2) $\simeq$ Sp(1) )

$$\array{ \pi_3^s & \simeq & \Omega_3^{fr} \\ [h_{\mathbb{H}}] & \leftrightarrow & [S^3] \,. }$$

Moreover, the relation $2 4 [S^3] \,\simeq\, 0$ is represented by the bordism which is the complement of 24 open balls inside the K3-manifold (Wang-Xu 10, Sec. 2.6).

Class in equivariant stable homotopy theory

Fix a finite subgroup $G \hookrightarrow SO(3)$ which does not come from $SO(2) \hookrightarrow SO(3)$ – i.e. not a cyclic group, but one of the dihedral groups or else the tetrahedral group or octahedral group or icosahedral group (by the ADE classification).

Regard both $S^7$ and $S^4$ as pointed topological G-spaces via the $SO(3)$-action induced via automorphisms of the quaternions, as above. Write

$$\Sigma^\infty_G S^7, \Sigma^\infty_G S^4 \in G Spectra$$

for the corresponding equivariant suspension spectra.

Notice that if we took trivial $G$, then in the stable homotopy category

$$[\Sigma^\infty S^7, \Sigma^\infty S^4] \simeq \mathbb{Z}/24$$

by the above. In contrast:¹

Proposition

In $G$-equivariant homotopy theory this becomes a non-torsion group, i.e.

$$[\Sigma^\infty_G S^7, \Sigma^\infty_G S^4]_G \simeq \mathbb{Z} \oplus \cdots$$

with the quaternionic Hopf fibration, regarded as a $G$-equivariant map, representing a non-torsion element.

Proof

First use the Greenlees-May decomposition which says that for any two $G$-equivariant spectra $X,Y$ and writing $\pi_\bullet(X), \pi_\bullet(Y)$ for their equivariant homotopy groups, organized as Mackey functors $H \mapsto \pi_n^H(X)$ for all subgroups $H \subset G$, then the canonical map

$$[X,Y]_G \longrightarrow \underset{n}{\oplus} Hom_{\mathcal{M}[G]}(\pi_n(X), \pi_n(Y))$$

is rationally an isomorphism.

With this we are reduced to showing that there exists $n \in \mathbb{Z}$ and a morphism of Mackey functors of equivariant homotopy groups $\pi_n(\Sigma^\infty_G S^7) \to \pi_n(\Sigma^\infty_G S^4)$ which is not a torsion element in the abelian hom-group of Mackey functors.

To analyse this, we use the tom Dieck splitting which says that the equivariant homotopy groups of equivariant suspension spectra $\Sigma^\infty_G X$ contain a direct summand which is simply the ordinary stable homotopy groups of the naive fixed point space $X^H$:

$$\pi_n^H(\Sigma^\infty_G X) \simeq \pi_n(\Sigma^\infty (X^H)) \oplus \cdots \,.$$

Now observe that the fixed points of the $SO(3)$-action on the quaternionic Hopf fibration that we are considering is just the real Hopf fibration:

$$(p_{\mathbb{H}})^{SO(3)} = p_{\mathbb{R}} \;\colon\; S^1 \longrightarrow S^1$$

since $SO(3)$ acts transitively on the quaternionic quaternions and fixes the real quaternions. By our assumption that $G \subset SO(3)$ does not come through $SO(2) \hookrightarrow SO(3)$ it follows that this statment is still true for $G$:

$$(p_{\mathbb{H}})^{G} = p_{\mathbb{R}} \;\colon\; S^1 \longrightarrow S^1 \,.$$

But the real Hopf fibration defines a non-torsion element in $\pi_0^S \simeq \mathbb{Z}$.

In conclusion then, at $n = 1$ and $H = G$ we find that the $G$-equivariant quaternionic Hopf fibration contributes a non-torsion element in

$$Hom_{Ab}(\pi_1^G(\Sigma^\infty_G S^7), \pi_1^G(\Sigma^\infty_G S^4))$$

which appears as a non-torsion element in

$$Hom_{\mathcal{M}[G]}( \pi_1(\Sigma^\infty_G S^7), \pi_1(\Sigma^\infty_G S^4) )$$

and hence in $[\Sigma^\infty_G S^7, \Sigma^\infty_G S^4]_G$.

See also at equivariant stable cohomotopy

Related concepts

• real Hopf fibration, complex Hopf fibration, octonionic Hopf fibration

• Calabi-Penrose fibration

• quaternionic projective space

References

The original article:

• Heinz Hopf, Über die Abbildungen von Sphären auf Sphäre niedrigerer Dimension, Fundamenta Mathematicae 25 1 (1935) 427-440 [eudml:212801]

Further discussion:

• Herman Gluck, Frank Warner, Wolfgang Ziller, The geometry of the Hopf fibrations, L’Enseignement Mathématique, 32 (1986), 173-198 [ResearchGate, pdf]

• Reiko Miyaoka, The linear isotropy group of $G_2/SO(4)$, the Hopf fibering and isoparametric hypersurfaces, Osaka J. Math. 30 2 (1993) 179-202 [Euclid]

• Ian Porteous, Clifford Algebras and the Classical Groups, Cambridge Studies in Advanced Mathematics, Cambridge University Press (1995) (doi:10.1017/CBO9780511470912)

• Machiko Hatsuda, Shinya Tomizawa, Coset for Hopf fibration and Squashing, Class. Quant. Grav. 26 225007 (2009) [arXiv:0906.1025, doi:10.1088/0264-9381/26/22/225007]

• Rustam Sadykov, §8.3 in: Elements of Surgery Theory, 2013 (pdf, pdf)

• Tyrone Cutler, p. 23 of: Fibrations IV (2020) [pdf, pdf]

Discussion in parameterized homotopy theory includes

• A. L. Cook, M. C. Crabb, Fiberwise Hopf structures on sphere bundles, J. London Math. Soc. (2) 48 (1993) 365-384 (pdf)

• Kouyemon Iriye, Equivariant Hopf structures on a sphere, J. Math. Kyoto Univ. Volume 35, Number 3 (1995), 403-412 (Euclid)

Discussion in homotopy type theory is in

• Ulrik Buchholtz, Egbert Rijke, The Cayley-Dickson Construction in Homotopy Type Theory (arXiv:1610.01134)

Noteworthy fiber products with the quaternionic Hopf fibration, notably exotic 7-spheres, are discussed in

• Llohann D. Sperança, Explicit Constructions over the Exotic 8-sphere (pdf, pdf)

---

1. The proof of prop. profited from Charles Rezk, who suggested here that the reduction to fixed points will make the real Hopf fibration give a non-torsion contribution, and from David Barnes who amplified the use of the Greenless-May splitting theorem. ↩