nLab equivariant sphere spectrum
Context
Stable Homotopy theory
Ingredients
Contents
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
The sphere spectrum in (global) equivariant stable homotopy theory.
Its RO(G)-graded homotopy groups are the equivariant version of the stable homotopy groups of spheres.
Definition
The -equivariant sphere spectrum is the equivariant suspension spectrum of the 0-sphere
for regarded as equipped with the (necessarily) trivial -action. It follows that for an orthogonal linear -representation then in RO(G)-degree the equivariant sphere spectrum is the corresponding representation sphere .
(e.g. Schwede 15, example 2.10)
Properties
Equivariant homotopy groups
Just as for the plain sphere spectrum, the equivariant homotopy groups of the equivariant sphere spectrum in ordinary integer degrees are all torsion, except at :
But in some RO(G)-degrees there may appear further non-torsion groups, see the examples below.
In degree 0, the tom Dieck splitting applied to the equivariant suspension spectrum gives that is the free abelian group on the set of conjugacy classes of subgroups of :
(e.g. Schwede 15, p. 64)
Examples
-equivariance
Consider the cyclic group of order 2 and write for the homotopy group in RO(G)-degree given by the representation on where acts by reflection on the first coordinates, and trivially on the remaining coordinates:
The following groups contain -summands:
-
(by the equivariant Hopf degree theorem, this Example)
-
(Araki-Iriye 82, theorem 8.7, p. 25) generated by the complex Hopf fibration (Araki-Iriye 82, p. 24)
-
generated by (Araki-Iriye 82, theorem 9.6, p. 27)
-
generated by (Araki-Iriye 82, theorem 10.11, p. 31)
-
generated by (Araki-Iriye 82, theorem 11.3, p. 32)
In addition we have
- generated by the quaternionic Hopf fibration (Araki-Iriye 82, prop. 10.1, p. 28 with theorem 10.11, p. 31)
In summary and more generally we have the following -equivariant stable homotopy groups of spheres in low bidegree:
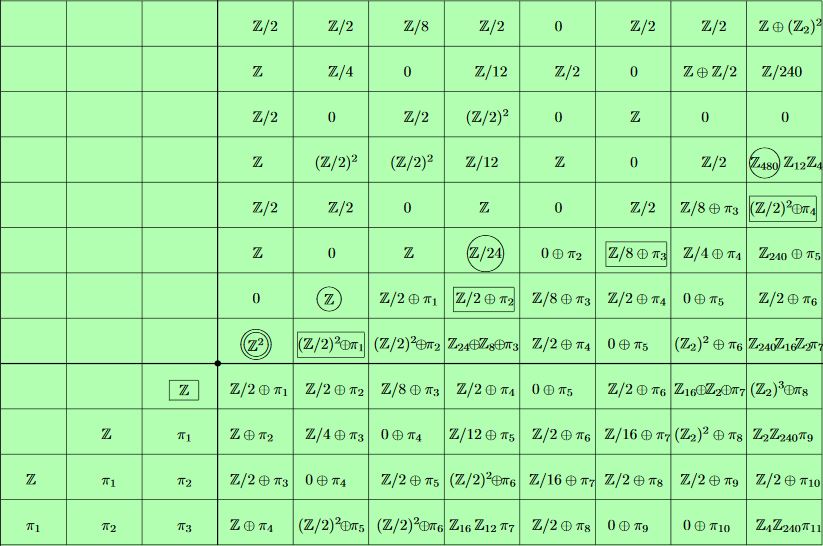
The table shows the -equivariant stable homotopy groups of spheres with increasing horizontally to the right, and increasing vertically upwards. The origin is the double-circled . The complex Hopf fibration generates , and the quaternionic Hopf fibration generates
graphics grabbed from Dugger 08, based on Araki-Iriye 82
(beware that Dugger 08 uses a different bi-degree labeling convention: the here is in Dugger 08, matching the coordinates of the above table)
Cyclic (-)equivariance
The global equivariant sphere spectrum for all the cyclic groups over the circle group is canonically a cyclotomic spectrum and as such is the tensor unit in the monoidal (infinity,1)-category of cyclotomic spectra (see there).
-equivariance
See at quaternionic Hopf fibration – Class in equivariant stable homotopy theory
Related concepts
-
The cohomology theory represented by the equivariant sphere spectrum is equivariant stable cohomotopy.
References
General
General lecture notes include
- Stefan Schwede, example 2.10 in Lectures on Equivariant Stable Homotopy Theory
Discussion in rational equivariant stable homotopy theory includes
- John Greenlees, Peter May, appendix A of Generalized Tate cohomology, Mem. Amer. Math. Soc. 113 (1995) no 543 (pdf)
The sphere spectrum in global equivariant homotopy theory is discussed in
-
John Rognes, Galois extensions of structured ring spectra (arXiv:math/0502183)
-
Markus Hausmann, Dominik Ostermayr, Filtrations of global equivariant K-theory (arXiv:1510.04011)
Relation to equivariant framed bordism
Proof that equivariant framed bordism homology theory is co-represented by the equivariant sphere spectrum:
- Czes Kosniowski, Equivariant Stable Homotopy and Framed Bordism, Transactions of the American Mathematical Society Vol. 219 (1976), pp. 225-234 (jstor:1997591)
-equivariance
Discussion of -equivariant homotopy groups for is in
-
Peter Landweber, On Equivariant Maps Between Spheres with Involutions, Annals of Mathematics Second Series, Vol. 89, No. 1 (Jan., 1969), pp. 125-137 (jstor)
-
Shôrô Araki, Kouyemon Iriye, Equivariant stable homotopy groups of spheres with involutions. I, Osaka J. Math. Volume 19, Number 1 (1982), 1-55. (Euclid:1200774828)
-
Kouyemon Iriye, Equivariant stable homotopy groups of spheres with involutions. II, Osaka J. Math. Volume 19, Number 4 (1982), 733-743 (euclid:1200775536)
-
Daniel Dugger, Daniel Isaksen, -equivariant and R-motivic stable stems, Proceedings of the American Mathematical Society 145.8 (2017): 3617-3627 (arXiv:1603.09305)
with exposition in
- Daniel Dugger, Motivic stable homotopy groups of spheres, talk at Third Arolla Conference on Algebraic Topology 2008 (pdf, pdf)
-equivariance
Discussion for is in
- M. C. Crabb, Periodicty in equivariant stable homotopy theory, in Mark Mahowald and Stewart Priddy (eds.) Algebraic Topology, Proceedings of the International Conference held March 21-24 (1988) Contemporary Mathematics, volume 96, 1989 (pdf, publisher page)
General background includes
Last revised on September 17, 2022 at 10:24:36. See the history of this page for a list of all contributions to it.