nLab electronic band structure

Idea

By Bloch-Floquet theory the available energies of electron-excitations in crystals depends smoothly on the momentum/wave number $k$ of the excitation, taking values in the Brillouin torus, and otherwise only on a discrete index set labelling the remaining “quantum numbers?” (the electron‘s orbitals?, spin. etc.). Fixing the latter values (and jointly denoting them $\mathbf{n}$, say), the given function $k \mapsto E_{\mathbf{n}}(k)$ (or rather its graph) is called the $\mathbf{n}$th electronic band (or just $\mathbf{n}$th band, for short) of the material.

Often, the values of $E_{\mathbf{n}}(-)$ are closely spaced as $\mathbf{n}$ varies in certain subsets of its allowed values. For instance if $\mathbf{n}$ includes the spin of the electrons and if there is a (typically small) spin-orbit coupling and no sizeable external magnetic field, then the energies $E_{n,\uparrow}(-)$ and $E_{n, \downarrow}$ differ (only) slightly. In these cases the graphs of these values jointly look approximately like a single but thickened curve (as such shown in the following schematic graphics), which is where the name “band” originates from.

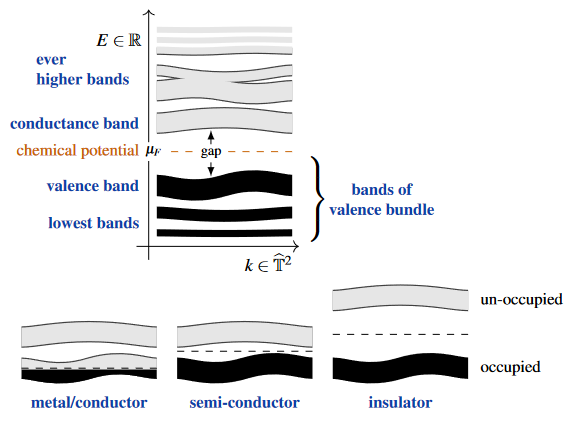
The band geometry around the electron chemical potential of a material controls its electrical conductivity:

(graphics from SS 22)

metal/conductor	the electron chemical potential is inside the valence band
insulator	the electron chemical potential is inside a large gap between (what is then) the valence- and conduction-band
semi-conductor	the electron chemical potential is inside a small gap between valence and conduction band
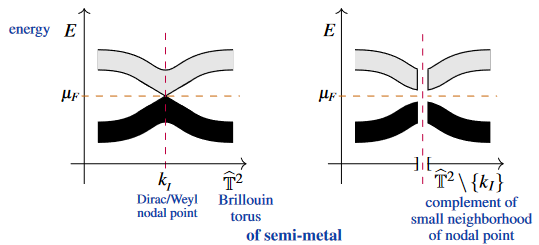
semi-metal	there is a large gap between valence and conduction band, except over a codimension$\geq 2$ locus, where the gap closes right at the chemical potential

(graphics from SS 22)

Related concepts

• Bloch-Floquet theory

• Berry connection

• dispersion relation

• energy band structure is also observed in “metamaterials” such as:

  • photonic crystals

  • phononic crystals

References

General

Textbook accounts:

• Karlheinz Seeger, Section 2 of: Semiconductor Physics, Advanced texts in physics, Springer (2004) $[$doi:10.1007/978-3-662-09855-4$]$

• Sheng San Li, Energy Band Theory, in S. S. Li, (ed.): Semiconductor Physical Electronics, Springer (2006) 61-104 $[$doi:10.1007/0-387-37766-2_4$]$

Lecture notes:

• David Tong, Chapter 2 of: Lectures on solid state physics (2017) $[$pdf, webpage$]$

Account with focus on topological phases of matter (topological insulators, semimetals etc.):

• David Vanderbilt, Berry Phases in Electronic Structure Theory – Electric Polarization, Orbital Magnetization and Topological Insulators, Cambridge University Press (2018) (doi:10.1017/9781316662205)

• Jérôme Cayssol, Jean-Noël Fuchs, Topological and geometrical aspects of band theory, J. Phys. Mater. 4 (2021) 034007 (arXiv:2012.11941, doi:10.1088/2515-7639/abf0b5)

See also:

• Wikipedia, Electronic band structure

Discussion of bands of metamaterials over hyperbolic spaces by a hyperbolic variant of Bloch's theorem:

• Joseph Maciejko, Steven Rayan, Hyperbolic band theory, Science Advances 7 36 (2021) [doi:10.1126/sciadv.abe9170]

• Adil Attar, Igor Boettcher, Selberg trace formula in hyperbolic band theory, Phys. Rev. E 106 034114 (2022) [arXiv:2201.06587, doi:10.1103/PhysRevE.106.034114]

Examples

The electronic band structure of graphene was predicted in

• Philip Russel Wallace, The Band Theory of Graphite, Phys. Rev. 71 (1947) 622 (doi:10.1103/PhysRev.71.622)

• Selberg trace formula in hyperbolic band theory Adil Attar, Igor Boettcher

For interacting electrons

• Yuejin Guo, Jean-Marc Langlois and William A. Goddard , Electronic Structure and Valence-Bond Band Structure of Cuprate Superconducting Materials, New Series, 239 4842 (1988) 896-899 $[$jstor:1700316$]$

• Jingsan Hu, Jianfei Gu, Weiyi Zhang, Bloch’s band structures of a pair of interacting electrons in simple one- and two-dimensional lattices, Physics Letters A 414 (2021) 127634 $[$doi:10.1016/j.physleta.2021.127634$]$