nLab semi-metal
Context
Solid state physics
-
basics
-
Examples
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
For quantum computation:
Contents
Idea
In condensed matter physics, a semi-metal is a crystalline material whose electronic band structure is such that there is a sizeable gap between the valence band and the conduction band (as for an insulator) except over a submanifold of “nodal loci” inside the Brillouin torus which is of positive codimension .
This terminology, which was established in the early 2000s, is meant to follow the older terminology semiconductor, which refers to the case where there is globally a gap between valence and conduction band, but just a small one. Notice that a global and large gap corresponds to an insulator, while the absence of a gap, hence the broad overlap of valence and conductions band, corresponds to a metal. Therefore a semi-metal behaves like an insulator for the bulk of its excitation modes, like a semiconductor for excitations close to the nodal loci, and almost like a metal for excitations right at the nodal loci; whence the terminology.
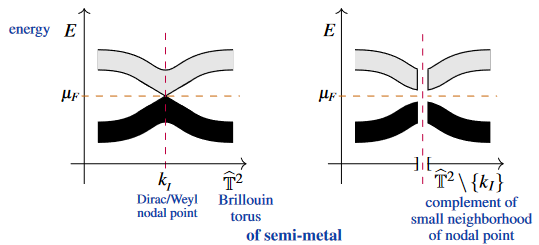 (graphics from SS 22)
(graphics from SS 22)
If the gap closure happens over an isolated point, one speaks of a nodal point proper, or more specifically of a Dirac point or Weyl point, indicating the “degeneracy” (multiplicity) of the energy eigenstates at the point (2 for Weyl, 4 for Dirac, see below). If the gap closes over a 1-dimensional manifold (a curve or a circle) one speaks of a nodal line.
Due to the gap on (a neighbourhood retract of) the complement of the nodal points/lines inside the Brillouin torus, the Berry connection is well-defined away from the nodal loci, and it tends to be flat in suitable hyperplanes there. It’s holonomy around codimension=2 nodal loci (ie. around nodal lines in 3d materials and nodal points in effectively 2d materials such as graphene, see also at defect brane) – known as a Berry phase – is then a property of the nodal locus alone, and to be interpreted as a measure for the “topological protection” of the gap over the nodal loci (e.g. FWDF 16, II.B, Vanderbilt 18, 5.5.2): Under adiabatic deformations of the material that do not excite modes above the gap, these nodal points may move and merge or split, but their total topological charge cannot change.
Therefore semi-metals with such non-trivial Berry phases are examples of topological phases of matter, and are sometimes called topological semi-metals, for emphasis. In fact, if the topological charges of the nodal loci in a semi-metal do happen to be trivial, then it is (in the deformation class of) a fully gapped insulator and may then be a topological insulator (if the twisted equivariant topological K-theory class of its valence bundle is non-trivial).
Properties
Phase decay via mass terms
Near nodal points in the Brillouin torus of a semi-metal, the dispersion relation exhibited by the energy bands is thought to be approximated by that of a massless Dirac equation/Weyl equation, whence the terminology Dirac point or Weyl point.
When the material’s parameters can be and are adiabatically tuned such that this dispersion relation turns into a massive Dirac equation, then the band gap at the former nodal crossing will “open up” in proportion to the coefficient of the effective mass term in the Dirac equation. If this happens to all nodal points (while keeping the band gap open everywhere else), one expects that the topological semi-metal phase decays into a topological insulator-phase.
A necessary condition for such a mass term to exist at all is that a further Clifford generator is represented on the Bloch-Hilbert space of electrons such that it skew-commutes with all Clifford momenta (e.g. Schnyder 18, Sec. II.A, Schnyder 20, Sec. 2.1, see also Freed & Hopkins 21, around Lem. 9.55).
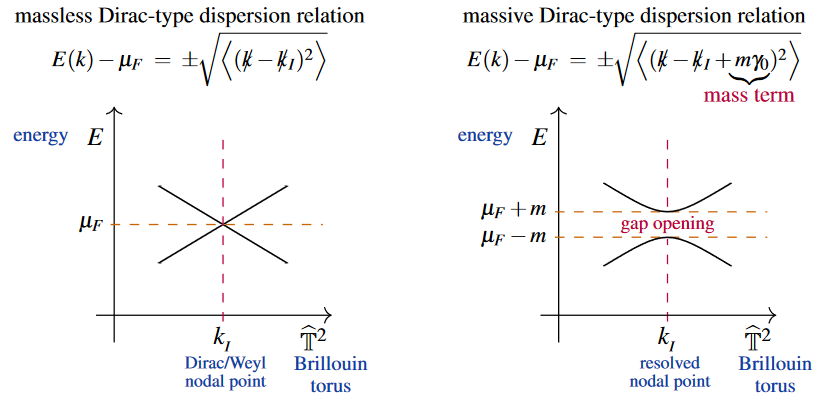
By Karoubi/Atiyah-Singer-type theorems, such gap-opening mass terms are expected to again be classified by topological K-theory groups (Chiu & Schnyder 14, Sec. A.2, reviewed in Schnyder 18, Sec. II.A, Schnyder 20, Sec. 2.1, following Morimoto & Furusaki 13, Sec. V, CTSR 15, Sec. III.C).
Beware:
-
This means that the topological semi-metal-phase must be classified in a group modulo the group of mass terms (cf. Freed & Hopkins 21, Thm. 9.63). The K-group of mass terms itself at best classifies aspects of the topological insulator-phase that the semi-metal phase may decay to.
-
The argument about single mass terms in a K-theory group of a point ignores the global topology of the valence bundle.
This is manifest already in the canonical example of the Haldane model, where for constant mass terms (as usually understood) the total topological charge of all nodal points combined is constrained to vanish.
Examples
The archetypical and original example of a semi-metal is graphene, where the gap closes over two Dirac points. (Or almost: a tiny spin-orbit coupling in graphene actually produces a tiny gap even at the would-be Dirac points, which however tends to be too small to be visible in practice. But if one will or would analyze graphene with an accuracy that does resolve this tiny gap-opening, then graphene will or would appear as a topological insulator instead of a semi-metal.)
After the synthesis of graphene, which is an effectively 2-dimensional material (an atomic mono-layer) much attention has shifted to the synthesis and understanding of 3-dimensional semi-metals.
Related concepts
References
General
Review:
-
Anton A. Burkov, Topological semimetals, Nature Materials 15 (2016) 1145–1148 [doi:10.1038/nmat4788, arXiv:1610.07866]
-
Jinyu Zou, Zhuoran He, Gang Xu: The study of magnetic topological semimetals by first principles calculations, npj Computational Materials 5 96 (2019) [doi:10.1038/s41524-019-0237-5]
-
Alexander S. Sergeev, section 10 of: Topological insulators and geometry of vector bundles, SciPost Physics Lecture Notes 67 (2023) [arXiv:2011.05004, doi:10.21468/SciPostPhysLectNotes.67]
-
Guo Chuan Thiang: Topological Semimetals, Encyclopedia of Mathematical Physics 2nd ed (2024) [arXiv:2407.12692]
General monographs:
-
Tomáš Bzdušek, Symmetry and topology of nodal semimetals, ETH (2017) [doi:10.3929/ethz-b-000216959]
-
David Vanderbilt, Section 5 of: Berry Phases in Electronic Structure Theory – Electric Polarization, Orbital Magnetization and Topological Insulators, Cambridge University Press (2018) (doi:10.1017/9781316662205)
Review with emphasis on mass terms:
-
Andreas P. Schnyder, Accidental and symmetry-enforced band crossings in topological semimetals, lecture notes (2018) [pdf, pdf]
-
Andreas P. Schnyder, Topological semimetals, lecture notes (2020) [pdf, pdf]
For references on graphene see also there.
Discussion focusing on 3-dimensional semi-metals with nodal lines:
-
Anton A. Burkov, M. D. Hook, Leon Balents, Topological nodal semimetals, Phys. Rev. B 84 (2011) 235126 [arXiv:1110.1089, doi:10.1103/PhysRevB.84.235126]
-
Ari M. Turner, Ashvin Vishwanath, Part I of: Beyond Band Insulators: Topology of Semi-metals and Interacting Phases, in: Topological Insulators, Contemporary Concepts of Condensed Matter Science 6 (2013) 293-324 arXiv:1301.0330, ISBN:978-0-444-63314-9
-
Bohm-Jung Yang, Naoto Nagaosa, Classification of stable three-dimensional Dirac semimetals with nontrivial topology, Nature Communications 5 (2014) 4898 (doi:10.1038/ncomms5898)
-
N. P. Armitage, Eugene Mele, Ashvin Vishwanath, Weyl and Dirac semimetals in three-dimensional solids, Rev. Mod. Phys. 90 015001 (2018) doi:10.1103/RevModPhys.90.015001
-
Jiaheng Li, Zetao Zhang, Chong Wang, Huaqing Huang, Bing-Lin Gu, Wenhui Duan, Topological semimetals from the perspective of first-principles calculations, Journal of Applied Physics 128, 191101 (2020) (doi:10.1063/5.0025396)
-
Faruk Abdulla, Ganpathy Murthy, Ankur Das, Stable nodal line semimetals in the chiral classes in three dimensions [arXiv:2401.02966]
Discussion of the -valued Berry phases around codimension=2 nodal loci in -symmetric (time-reversal + inversion invariant) semi-metals:
-
Dan-Wei Zhang, Y. X. Zhao, Rui-Bin Liu, Zheng-Yuan Xue, Shi-Liang Zhu, Z. D. Wang, Quantum simulation of exotic PT-invariant topological nodal loop bands with ultracold atoms in an optical lattice, Phys. Rev. A 93 (2016) 043617 (arXiv:1601.00371, doi:10.1103/PhysRevA.93.043617)
(see sec II.A, these authors stand out as mentioning the relevant KO-theory)
-
Chen Fang, Hongming Weng, Xi Dai, Zhong Fang, Topological nodal line semimetals, Chinese Phys. B 25 (2016) 117106 (arXiv:1609.05414, doi:10.1088/1674-1056/25/11/117106)
(see sec II.B)
More mathematical discussion of the case of Chern semi-metals:
-
Varghese Mathai, Guo Chuan Thiang, Global topology of Weyl semimetals and Fermi arcs, J. Phys. A: Math. Theor. 50 (2017) 11LT01 [arXiv:1607.02242, doi:10.1088/1751-8121/aa59b2]
-
Varghese Mathai, Guo Chuan Thiang, Differential Topology of Semimetals, Commun. Math. Phys. 355 (2017) 561–602 [arXiv:1611.08961, doi:10.1007/s00220-017-2965-z]
Discussion of (classification of) Dirac/Weyl mass terms:
- Ching-Kai Chiu, Andreas P. Schnyder, Section A.2 of: Classification of reflection-symmetry-protected topological semimetals and nodal superconductors, Phys. Rev. B 90 205136 (2014) doi:10.1103/PhysRevB.90.205136
following:
-
Takahiro Morimoto and Akira Furusaki, Sec. V of: Topological classification with additional symmetries from Clifford algebras, Phys. Rev. B 88 (2013) 125129 (arXiv:1306.2505, doi:10.1103/PhysRevB.88.125129)
-
Ching-Kai Chiu, Jeffrey C.Y. Teo, Andreas P. Schnyder, Shinsei Ryu, Section III.C of Classification of topological quantum matter with symmetries, Rev. Mod. Phys. 88 (2016) 035005 (arXiv:1505.03535, doi:10.1103/RevModPhys.88.035005)
Pedagogical example:
- Delft Topology Course team, Haldane model, Berry curvature, and Chern number - First try, Second try
Related discussion of Dirac mass terms is in:
- Daniel S. Freed, Michael J. Hopkins, Reflection positivity and invertible topological phases, Geom. Topol. 25 (2021) 1165-1330 [arXiv:1604.06527, doi:10.2140/gt.2021.25.1165]
Lists of actual semi-metals:
- Md. Rakibul Karim Akand. Catalog of magnetic topological semimetals, AIP Advances 10 095222 (2020) [doi:10.1063/5.0020096]
Simulation of Dirac semimetals with lattice field theory:
- Lattice field theory simulations of Dirac semimetals, Annals of Physics 391 (2018) 278-292 [doi:10.1016/j.aop.2018.02.016]
and other numerical calculuations:
-
The study of magnetic topological semimetals by first principles calculations, npj Computational Materials 5 96 (2019) [doi:10.1038/s41524-019-0237-5]
-
Topological semimetals from the perspective of first-principles calculations, Journal of Applied Physics 128 (2020) 191101 [doi:10.1063/5.0025396]
On strongly-coupled topological semimetals:
-
Koji Hashimoto, Shunichiro Kinoshita, Keiju Murata, Takashi Oka, Holographic Floquet states: (I) A strongly coupled Weyl semimetal, J. High Energ. Phys. 2017 127 (2017) [arXiv:1611.03702, doi:10.1007/JHEP05(2017)127]
-
Diana M Kirschbaum, Monika Lužnik, Gwenvredig Le Roy, Silke Paschen, How to identify and characterize strongly correlated topological semimetals, J. Phys. Mater. 7 (2024) 012003 [doi:10.1088/2515-7639/ad0f30a, arXiv:2308.11318]
-
Yongjun Ahn, Matteo Baggioli, Yan Liu, Xin-Meng Wu, Chiral magnetic waves in strongly coupled Weyl semimetals, J. High Energ. Phys. 2024 124 (2024) [arXiv:2401.07772, doi:10.1007/JHEP03(2024)124]
and relation to topological order:
-
Chong Wang, Lei Gioia, Anton A. Burkov, Fractional Quantum Hall Effect in Weyl Semimetals, Phys. Rev. Lett. 124 096603 (2020) [doi:10.1103/PhysRevLett.124.096603]
-
Manisha Thakurathi, Anton A. Burkov, Theory of the fractional quantum Hall effect in Weyl semimetals, Phys. Rev. B 101 235168 (2020) [doi:10.1103/PhysRevB.101.235168, arXiv:2005.13545, arXiv:2005.13545]
“while we focused on fully gapped states […] it also makes sense to consider gapless strongly correlated states with the same property. Such states may be accessed easily within the formalism, presented above
-
Dan Sehayek, Manisha Thakurathi, Anton A. Burkov, Charge density waves in Weyl semimetals, Phys. Rev. B 102 115159 (2020) [doi:10.1103/PhysRevB.102.115159]
-
Jinmin Yi, Xuzhe Ying, Lei Gioia, Anton A. Burkov, Topological order in interacting semimetals, Phys. Rev. B 107 115147 (2023) [arXi:2301.03628, doi:10.1103/PhysRevB.107.115147]
-
Hongshuang Liu, Jiashuo Liang, Taiyu Sun, Liying Wang: Recent progress in topological semimetal and its realization in Heusler compounds, Materials Today Physics 41 (2024) 101343 [doi:10.1016/j.mtphys.2024.101343]
On Weyl-Kondo semimetals:
-
Hsin-Hua Lai, Sarah E. Grefe, Silke Paschen, Qimiao Si, Weyl–Kondo semimetal in heavy-fermion systems, PNAS 115 1 (2017) 93-97 [doi:10.1073/pnas.1715851115]
-
Lei Chen, C. Setty, H. Hu et al.: Topological Semimetal driven by Strong Correlations and Crystalline Symmetry,
Nat. Phys. 18 1341–1346 (2022) [arXiv:2107.10837, doi:10.1038/s41567-022-01743-4&rbrack
and background on “heavy fermions”:
- Norbert Grewe, Frank Steglich, Heavy fermions, Chapter 97 in: Handbook on the Physics and Chemistry of Rare Earths 14 (1991) 343-474 [doi:10.1016/S0168-1273(05)80103-5]
Holographic description
On holographic descriptions of topological semimetals via the AdS-CMT correspondence:
-
Karl Landsteiner, Yan Liu, The holographic Weyl semi-metal, Physics Letters B 753 (2016) 453-457 [arXiv:1505.04772, doi:10.1016/j.physletb.2015.12.052]
-
Karl Landsteiner, Yan Liu, Ya-Wen Sun, Quantum phase transition between a topological and a trivial semimetal from holography, Phys. Rev. Lett. 116 081602 (2016) [arXiv:1511.05505, doi:10.1103/PhysRevLett.116.081602]
-
Ling-Long Gao, Yan Liu, Hong-Da Lyu, Black hole interiors in holographic topological semimetals [arXiv:2301.01468]
-
Masataka Matsumoto, Mirmani Mirjalali, Ali Vahedi, Non-Linear Dynamics and Critical Phenomena in the Holographic Landscape of Weyl Semimetals [arXiv:2405.06484]
-
Nishal Rai, Karl Landsteiner: Hydrodynamic Modes of Holographic Weyl Semimetals [arXiv:2408.06192]
Review:
- Karl Landsteiner, Yan Liu, Ya-Wen Sun, Holographic Topological Semimetals, Sci. China Phys. Mech. Astron. 63 250001 (2020) [arXiv:1911.07978, doi:10.1007/s11433-019-1477-7]
Some of the above material is taken from
- Hisham Sati, Urs Schreiber: Topological Quantum Computation in TED-K, PlanQC 2022 33, (15 Sep 2022) [arXiv:2209.08331, slides: pdf, video: YT]
Anyons in momentum-space
On non-trivial braiding of nodal points in the Brillouin torus of topological semi-metals (“braiding in momentum space”):
-
Junyeong Ahn, Sungjoon Park, Bohm-Jung Yang, Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle, Phys. Rev. X 9 (2019) 021013 [doi:10.1103/PhysRevX.9.021013, arXiv:1808.05375]
“here are band crossing points, henceforth called vortices”
-
QuanSheng Wu, Alexey A. Soluyanov, Tomáš Bzdušek, Non-Abelian band topology in noninteracting metals, Science 365 (2019) 1273-1277 [doi:10.1126/science.aau8740, arXiv:1808.07469]
“fundamental group of complement of nodal points/lines considered above (3)”
-
Apoorv Tiwari, Tomáš Bzdušek, Non-Abelian topology of nodal-line rings in PT-symmetric systems, Phys. Rev. B 101 (2020) 195130 [doi:10.1103/PhysRevB.101.195130]
“a new type non-Abelian ‘braiding’ of nodal-line rings inside the momentum space”
-
Adrien Bouhon, QuanSheng Wu, Robert-Jan Slager, Hongming Weng, Oleg V. Yazyev, Tomáš Bzdušek, Non-Abelian reciprocal braiding of Weyl points and its manifestation in ZrTe, Nature Physics 16 (2020) 1137-1143 [doi:10.1038/s41567-020-0967-9, arXiv:1907.10611]
“Here we report that Weyl points in three-dimensional (3D) systems with symmetry carry non-Abelian topological charges. These charges are transformed via non-trivial phase factors that arise upon braiding the nodes inside the reciprocal momentum space.”
Braiding of Dirac points in twisted bilayer graphene:
-
Jian Kang, Oskar Vafek: Non-Abelian Dirac node braiding and near-degeneracy of correlated phases at odd integer filling in magic angle twisted bilayer graphene, Phys. Rev. B 102 (2020) 035161 [doi:10.1103/PhysRevB.102.035161, arXiv:2002.10360]
-
Bin Jiang, Adrien Bouhon, Zhi-Kang Lin, Xiaoxi Zhou, Bo Hou, Feng Li, Robert-Jan Slager, Jian-Hua Jiang: Experimental observation of non-Abelian topological acoustic semimetals and their phase transitions, Nature Physics 17 (2021) 1239-1246 [doi:10.1038/s41567-021-01340-x, arXiv:2104.13397]
(analog realization in phononic crystals)
Here, we consider an exotic type of topological phases beyond the above paradigms that, instead, depend on topological charge conversion processes when band nodes are braided with respect to each other in momentum space or recombined over the Brillouin zone. The braiding of band nodes is in some sense the reciprocal space analog of the non-Abelian braiding of particles in real space. […] we experimentally observe non-Abelian topological semimetals and their evolutions using acoustic Bloch bands in kagome acoustic metamaterials. By tuning the geometry of the metamaterials, we experimentally confirm the creation, annihilation, moving, merging and splitting of the topological band nodes in multiple bandgaps and the associated non-Abelian topological phase transitions
-
Haedong Park, Stephan Wong, Xiao Zhang, and Sang Soon Oh, Non-Abelian Charged Nodal Links in a Dielectric Photonic Crystal, ACS Photonics 8 (2021) 2746–2754 [doi:10.1021/acsphotonics.1c00876]
-
Siyu Chen, Adrien Bouhon, Robert-Jan Slager, Bartomeu Monserrat, Non-Abelian braiding of Weyl nodes via symmetry-constrained phase transitions (formerly: Manipulation and braiding of Weyl nodes using symmetry-constrained phase transitions), Phys. Rev. B 105 (2022) L081117 [doi:10.1103/PhysRevB.105.L081117, arXiv:2108.10330]
“Our work opens up routes to readily manipulate Weyl nodes using only slight external parameter changes, paving the way for the practical realization of reciprocal space braiding.”
-
Bo Peng, Adrien Bouhon, Robert-Jan Slager, Bartomeu Monserrat, Multi-gap topology and non-Abelian braiding of phonons from first principles, Phys. Rev. B 105 (2022) 085115 [arXiv:2111.05872, doi:10.1103/PhysRevB.105.085115]
(analog realization in phononic crystals)
new opportunities for exploring non-Abelian braiding of band crossing points (nodes) in reciprocal space, providing an alternative to the real space braiding exploited by other strategies.
Real space braiding is practically constrained to boundary states, which has made experimental observation and manipulation difficult; instead, reciprocal space braiding occurs in the bulk states of the band structures and we demonstrate in this work that this provides a straightforward platform for non-Abelian braiding.
-
Bo Peng, Adrien Bouhon, Bartomeu Monserrat, Robert-Jan Slager, Phonons as a platform for non-Abelian braiding and its manifestation in layered silicates, Nature Communications 13 423 (2022) [doi:10.1038/s41467-022-28046-9]
(analog realization in phononic crystals)
it is possible to controllably braid Kagome band nodes in monolayer using strain and/or an external electric field.
-
Haedong Park, Wenlong Gao, Xiao Zhang, Sang Soon Oh, Nodal lines in momentum space: topological invariants and recent realizations in photonic and other systems, Nanophotonics 11 11 (2022) 2779–2801 [doi:10.1515/nanoph-2021-0692]
(analog realization in photonic crystals)
-
Adrien Bouhon, Robert-Jan Slager, Multi-gap topological conversion of Euler class via band-node braiding: minimal models, PT-linked nodal rings, and chiral heirs [arXiv:2203.16741]
See also:
-
Robert-Jan Slager, Adrien Bouhon, Fatma Nur Ünal, Floquet multi-gap topology: Non-Abelian braiding and anomalous Dirac string phase, Nature Communications 15 1144 (2024) [arXiv:2208.12824, doi:10.1038/s41467-024-45302-2]
-
Huahui Qiu et al., Minimal non-abelian nodal braiding in ideal metamaterials, Nature Communications 14 1261 (2023) [doi:10.1038/s41467-023-36952-9]
-
Wojciech J. Jankowski, Mohammedreza Noormandipour, Adrien Bouhon, Robert-Jan Slager: Disorder-induced topological quantum phase transitions in Euler semimetals, Phys. Rev. B 110 (2024) 064202 [arXiv:2306.13084, doi:10.1103/PhysRevB.110.064202]
-
Seung Hun Lee, Yuting Qian, Bohm-Jung Yang, Euler band topology in spin-orbit coupled magnetic systems [arXiv:2404.16383]
“Based on first-principles calculations, we report that such nodal point braiding in 2D electronic bands can be realized in a MSWI candidate, the bilayer with in-plane ferromagnetism under pressure. […] one can expect that the braiding of nodes can be achieved in 2D bilayer under the influence of an external in-plane Zeeman field.”
Incidentally, references indicating that the required toroidal (or yet higher genus) geometry for anyonic topological order in position space is dubious (as opposed to the evident toroidal geometry of the momentum-space Brillouin torus): Lan 19, p. 1, ….
Exposition:
-
Gunnar F. Lange: Multi-gap topology & non-abelian braiding in -space, talk at University of Oslo (Feb 2023) pdf]
-
Adrien Bouhon: Non-Abelian and Euler multi-gap topologies in crystalline materials, talk at: Quantum Information and Quantum Matter, CQTS @ NYU Abu Dhabi (May 2023) pdf]
Knotted nodal lines in 3d semimetals
Beware that various authors consider braids/knots formed by nodal lines in 3d semimetals, i.e. knotted nodal lines in 3 spatial dimensions, as opposed to worldlines (in 2+1 spacetime dimensions) of nodal points in effectively 2d semimetals needed for the anyon-braiding considered above.
An argument that these nodal lines in 3d space, nevertheless, may be controlled by Chern-Simons theory:
- Biao Lian, Cumrun Vafa, Farzan Vafa, Shou-Cheng Zhang, Chern-Simons theory and Wilson loops in the Brillouin zone, Phys. Rev. B 95 (2017) 094512 [doi:10.1103/PhysRevB.95.094512]
Last revised on June 27, 2025 at 12:03:24. See the history of this page for a list of all contributions to it.