nLab valence bundle
Context
Solid state physics
-
basics
-
Examples
Contents
Idea
General
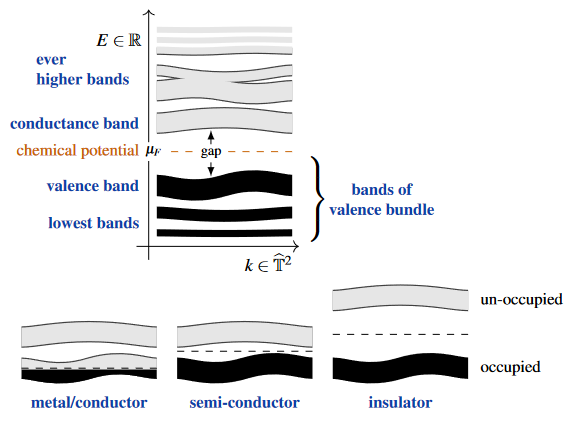
For a crystalline material, Bloch-Floquet theory shows that the Hilbert space of quantum states of the electrons (in the background of the atoms/nuclei at the crystal sites) is naturally the space of sections of a separable Hilbert space-bundle over the Brillouin torus, and the Hamiltonian is the direct integral of Bloch Hamiltonians? on its fibers, whose eigenvalues constitute the electronic energy bands. If the chemical potential of the electrons lies in a gap between two such electronic energy bands, then this Hilbert space bundle has a well-defined sub-bundle of Bloch states with energy below the chemical potential.
One says that the vectors in this vector bundle are the electron quantum states which are “filled” and one says that the vector bundle over the Brillouin torus which these form is the valence bundle of the system, and that the band formed by (the graph) of the corresponding energy eigenvalues is the valence band.
The orthogonal complement of the valence bundle inside the ambient Bloch Hilbert bundle would be known as the conduction bundle, though this term is not widely used. But the (lowest) band which is constituted by the corresponding energy eigenvalues is commonly known as the conduction band.
 (graphics from SS 22)
(graphics from SS 22)
Remark
Sometimes the valence bundle is referred to as a “Bloch bundle”, eg. Panati 06. This can be confusing, since the latter term would more naturally apply to the full Hilbert bundle of all Bloch states.
Remark
For metals the chemical potential is not inside a gap, and a valence sub-bundle is not really well-defined, though the valence band is still defined. For semi-metals there is a well-defined valence bundle on the complement of its nodal points in the Brillouin torus.
Classification
As a sub-bundle of the full a Hilbert space bundle of a quantum system, the valence bundle is naturally identified not up to isomorphism but up to ambient isomorphism, hence up to Murray-von Neumann equivalence?. In fact, it has been argued to be physically classified by its class in topological K-theory (i.e. the Grothendieck group completion of the semigroup of Murray-von Neumann equivalence classes under direct sum of vector bundles), or rather by the twisted equivariant K-theory reflecting the material’s quantum symmetries. This is the statement of the K-theory classification of topological phases of matter.
Related concepts
References
The valence/conduction bands are discussed in any text on solid state physics.
The valence bundle is sometimes called the Bloch bundle:
- Gianluca Panati, Triviality of Bloch and Bloch-Dirac bundles, Ann. Henri Poincaré 8 (2007) 995-1011. (arXiv:math-ph/0601034, doi:10.1007/s00023-007-0326-8)
For mathematical discussion of the actual valence bundle see:
- Daniel Freed, Gregory Moore, Prop. D.13 in: Twisted equivariant matter, Ann. Henri Poincaré (2013) 14: 1927 (arXiv:1208.5055)
Last revised on January 12, 2025 at 12:57:22. See the history of this page for a list of all contributions to it.