nLab symmetry protected topological phase
Context
Solid state physics
-
basics
-
Examples
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
For quantum computation:
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Idea
In solid state physics, by a phase of matter which is
- symmetry protected topological (“SPT”, Gu & Wen 09, PBTO 09)
or more generally
- symmetry enriched topological (“SET”, CGLW 11, p. 3, CLM 12, p. 2)
one means a topological phase of matter which is -equivariantly non-trivial, in that it cannot be adiabatically deformed to a trivial phase while respecting some -symmetry. In case of SPT one in addition requires that the underlying topological phase (forgetting the symmetry) is trivial, while in case of SET this constraint is not implied.
Since, if one forgets (theoretically) the -equivariance, a -equivariantly non-trivial SPT may be trivial as a plain topological phase, and two distinct SETs may be equivalent as plain topological phases, one may regard the -symmetry as “protecting” an SPT phase from decaying and as “enriching” one plain phase to several distinct SET phases – whence the terminology.
In other words:
-
distinct SPT/SET phases with a given symmetry cannot be adiabatically deformed into each other, in particular not without going through a phase transition, if the whole deformation preserves the symmetry;
-
but they may possibly be transformed into each other this way if the symmetry is broken during the deformation.
There are the following types of symmetry groups to which the concept of crystalline SPT/SET phases applies (as well as to any of their semidirect combinations):
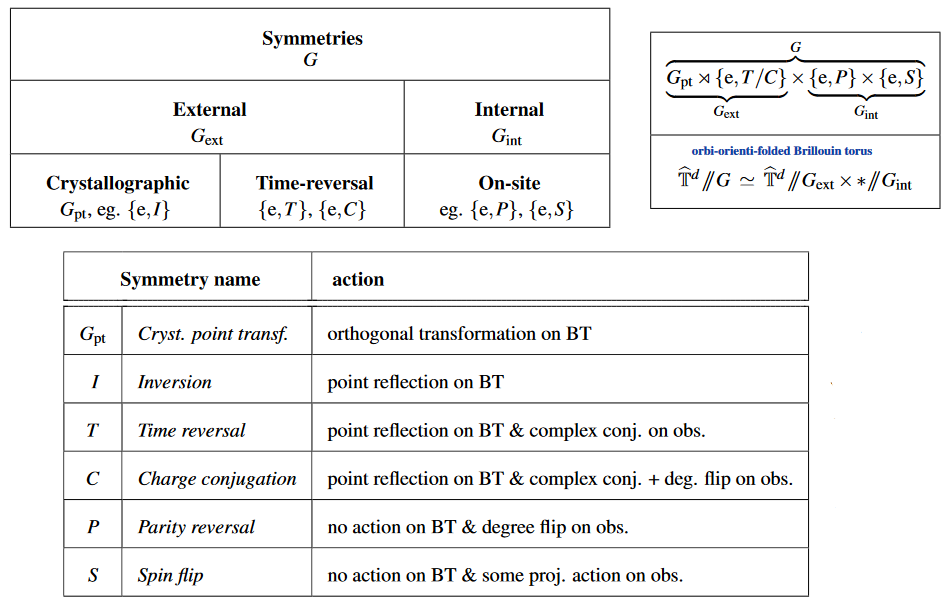
-
may be an “external” spatial symmetry, namely a subgroup of the crystallographic point group of the underlying crystalline material, canonically acting on the Brillouin torus (BT) ;
for example inversion is the sign reversal involution on .
If a topological insulator-phase is “protected” by a crystallographic point group symmetry this way (possibly including time-reversal symmetry), then one speaks of a topological crystalline insulator.
-
may be time reversal symmetry or charge reversal, which acts as on the Brillouin torus, but in addition acts on the Hamiltonian by complex conjugation and, respectively, sign reversal;
-
may be an internal symmetry which acts not on the position but on the “internal degrees of freedom” of (electrons in the) substance, which are, typically, located at each atomic site (whence also: “on-site symmetry”).
The prime example of an internal symmetry are (finite) subgroups of the Spin(3)SU(2)-group which acts on the electron spins. This will be a symmetry to the extent that spin interactions (such as the spin-orbit coupling or the intrinsic Lorentz force due to an external magnetic field) are negligible.
Remark
(terminology)
-
Beware that some authors insist on using the specific term “SPT” only for items further down in this list. For instance the claim below that SPT’s are “classified by group cohomology” applies really to the last item (see below).
The first two items instead, for the case of free fermion systems at least, are expected to have a classification in twisted equivariant topological K-theory (see at K-theory classification of topological phases of matter).
For the conceptual relation between these cases see further below.
-
Beware that the first articles on the topic (Gu & Wen 09, PBTO 09) actually used the term “symmetry protected topological order”. This could be perceived as somewhat of a misnomer, since in examples the (symmetry protected) “topological order” is often trivial (in that the ground state is non-degenerate and/or the Berry connection is abelian) even though the underlying (symmetry protected) topological phase is non-trivial (ie. the valence bundle of a topological insulator has a non-trivial K-class).
Due to this problem, the original authors argued that “SPT” could also stand for “symmetric protected trivial order” (X.-G. Wen, Sep 18, 2014). But then it seems more descriptive (and now fairly widely accepted) to speak of “symmetry protected topological phase”. (See also at red herring principle.)
Examples
Spatial symmetry
-
The topological insulator/semi-metal-phase of graphene is protected by time-reversal symmetry (and inversion symmetry ), and for this historical reason this - and/or -symmetry protection is taken by some authors to be the default meaning of topological insulator.
-
Removing the /-protection of the phase of graphene leads to un-protected Chern insulators such as (modeled by) the Haldane model.
For more on spatial-SPT topological crystalline insulator-phases, see there for concrete examples.
Internal symmetry
- The first example of SPT order is the Haldane phase of the Heisenberg model spin-1 chain (Haldane 83). It is a SPT phase protected by the internal symmetry -group acting on the electron spin (often referred to in this context as a projective representation of ).
More examples of internal-SPT: Ye & Wen 13, CLV 14, Yang-Liu 18 …
Properties
Classification
Spatial symmetries
Symmetry protected crystalline phases where the dynamics of the electrons may approximately be regarded free (but subject to the the atomic lattice Coulomb background field, see here) are thought to be classified by twisted equivariant topological K-theory of the Brillouin torus. This is the statement of the K-theory classification of topological phases of matter.
Beware that this case has mostly been discussed for CPT-symmetries such as time-reversal symmetry (see at topological insulator) and for crystallographic symmetries (see at topological crystalline insulator), not so much for internal (“on site”) symmetries (but see Wen 12).
Internal symmetries
In contrast, a widely cited claim CGLW 11 asserts (motivation is offered in CLW 11, Sec. V) that “bosonic” SPT orders for an internal symmetry group are given by group cohomology of with coefficients in the circle group and in degree , for the effective dimension of the given material (in practice: ). This claim was generalized to fermionic SPT orders via a kind of group-supercohomology (Gu & Wen14).
From X.-G. Wen (2013, in rev 1):
So the group (super-)cohomology theory may allow us to classify all SPT orders even for interacting systems, which include interacting topological insulator/superconductor.
But conceptual problems have remained with this proposal:
this classification is now known not to be complete
From Xiong 18:
Despite tremendous progress, a complete classification of SPT phases for arbitrary symmetries in arbitrary dimensions remains elusive. A number of classification proposals have been made in the general case: the Borel group cohomology proposal CGLW11, the oriented cobordism proposal, the Freed-Hopkins proposal, and Kitaev’s proposal in the bosonic case; and the group supercohomology proposal GW14, the spin cobordism proposal, the Freed-Hopkins proposal, and Kitaev’s proposal in the fermionic case. These proposals give differing predictions in certain dimensions for certain symmetry groups that cannot be attributed to differences in definitions or conventions. While more careful analysis has uncovered previously overlooked phases and input from topological field theories has brought us closer than ever to our destination, we believe that we can do much more.
From BBCW 19, p. 3:
Although a remarkable amount of progress has been made on these deeply interrelated topics, a completely general understanding is lacking, and many questions remain. For example, although there are many partial results, the current understanding of fractionalization of quantum numbers, along with the classification and characterization of SETs is incomplete.
Moreover, while there have been many results towards understanding the properties of extrinsic defects in topological phases, there has been no general systematic understanding and, in particular, no concrete method of computing all the rich topological properties of the defects for an arbitrary topological phase. The study of topological phase transitions between different topological phases is also missing a general theory. In this paper, we develop a general systematic framework to understand these problems.
The proposal of BBCW 19 (may not yet have a physics “proof” either, but) is conceptually transparent: The authors assume, as often done, that a topological order with anyonic defects is characterized by a unitary fusion category , and then propose that a -SPT-phase with this underlying topological order is what we may equivalently recognize as:
-
the equivalence class of an ∞-action of on , namely
-
the cohomology-class of a 2-group-homomorphism from to the automorphism 2-group of :
(1)(this is essentially BBCW 19, (1) – where it says “group action”, but later from (81) on (p. 14) it transpires that the correct 2-group-action is indeed meant),
namely:
-
the pseudonatural transformation-class of a weak 2-functor
from the delooping groupoid of to that delooping 2-groupoid of the automorphism 2-group of .
This is plausible (relative to the assumption that characterizes the un-proteced topological order) since under an “internal symmetry” one wants to mean a global group action under which all other constructions have equivariant-structure, and (1) is exactly the data that equips anyon-species (the simple objects of ) and their fusion (the tensor product) and braiding (the braiding) with such -equivariant structure.
But neither of these proposals connects recognizably to the twisted equivariant K-theory classification of topological phases (TE-K). While the latter may not apply to all cases of symmetry symmetry protected topological phases, it certainly applies to some of them, and it currently stands out among all other proposals on the classification of topological phases of matter as being the one with the most detailed support by theory and experiment. Therefore it would be reassuring to see how any other classification proposal plausibly connects to the TE-K proposal in appropriate special cases (notably for phases well-approximated by free fermion dynamics).
Conversely, inspection of the mathematical construction of twisted equivariant K-theory (as made explicit in SS 21, (4.1.28)) readily reveals the evident way in which it subsumes internal symmetries and how the resulting structure has an equivalent expression in terms of ∞-group cohomology. This is an immediate consequence of the mapping stack--adjunction, as shown the following diagram
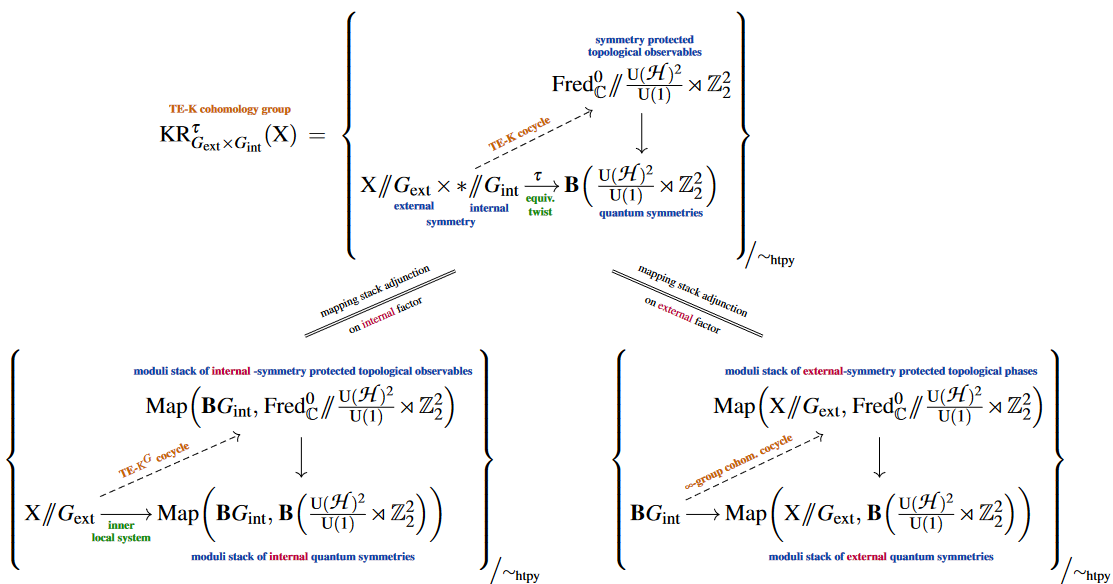
(graphics from SS 22b)
Here the mapping stack adjunction…
-
…on the internal symmetry group factor (shown on the right) manifestly identifies the TE-K cohomology-group at the top with an ∞-group cohomology group of which plausibly matches, as before, the intuition one would have about internal symmetry groups acting on K-theoretically classified phases of matter;
-
..on the external symmetry group factor (shonw on the left) manifestly identifies the TE-K cohomology-group at the top with an inner local system-twisted sector of -fixed TE-K-theory. Just this sector has been shown (in SS 22a, by recourse to the hypergeometric construction of KZ solutions) to host SU(2)-anyon wavefunctions (namely affine Lie algebra-conformal blocks) constituting braid representations, and hence exactly the structure expected in a symmetry protected topological order.
Related concepts
References
Original articles
-
Zheng-Cheng Gu, Xiao-Gang Wen, Tensor-Entanglement-Filtering Renormalization Approach and Symmetry Protected Topological Order, Phys. Rev. B 80 155131 (2009) arXiv:0903.1069, doi:10.1103/PhysRevB.80.155131
-
Frank Pollmann, Erez Berg, Ari M. Turner, Masaki Oshikawa, Symmetry protection of topological order in one-dimensional quantum spin systems, Phys. Rev. B 85 075125 (2012) [arXiv:0909.4059, doi:10.1103/PhysRevB.85.075125]
-
Xie Chen, Zheng-Xin Liu, Xiao-Gang Wen, 2D symmetry protected topological orders and their protected gapless edge excitations, Phys. Rev. B 84, 235141 (2011);
See also:
-
Peng Ye, Xiao-Gang Wen, Projective construction of two-dimensional symmetry-protected topological phases with , , or symmetries, Phys. Rev. B 87 195128 (2013) [doi:10.1103/PhysRevB.87.195128, arXiv:1212.2121]
-
Gil Young Cho, Yuan-Ming Lu, and Joel E. Moore, Gapless edge states of background field theory and translation-symmetric spin liquids, Phys. Rev. B 86 125101 (2012) [arXiv:10.1103/PhysRevB.86.125101]
-
Xie Chen, Yuan-Ming Lu, Ashvin Vishwanath: Symmetry-protected topological phases from decorated domain walls, Nature Communications 5 3507 (2014) [doi:10.1038/ncomms4507]
-
Juven Wang, Zheng-Cheng Gu, Xiao-Gang Wen, Field theory representation of gauge-gravity symmetry-protected topological invariants, group cohomology and beyond, Phys. Rev. Lett. 114 (2015) 031601 [arxiv:1405.7689, doi:10.1103/PhysRevLett.114.031601]
-
Jian Yang, Zheng-Xin Liu, Irreducible Projective Representations and Their Physical Applications, J. Phys. A: Math. Theor. 51 025207 (2018) doi:10.1088/1751-8121/aa971a, arXiv:1605.05805
-
Yoshiko Ogata, An invariant of symmetry protected topological phases with on-site finite group symmetry for two-dimensional Fermion systems arXiv:2110.04672
Reviews
-
Ching-Kai Chiu, Jeffrey C.Y. Teo, Andreas P. Schnyder Shinsei Ryu, Classification of topological quantum matter with symmetries, Rev. Mod. Phys. 88 035005 (2016) arXiv:1505.03535, doi:10.1103/RevModPhys.88.035005
-
Bei Zeng, Xie Chen, Duan-Lu Zhou, Xiao-Gang Wen:
Sec. 10 of: Quantum Information Meets Quantum Matter – From Quantum Entanglement to Topological Phases of Many-Body Systems, Quantum Science and Technology (QST), Springer (2019) arXiv:1508.02595, doi:10.1007/978-1-4939-9084-9
-
Tudor D. Stanescu, Section 4.1 of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press (2020) [ISBN:9780367574116]
-
Alexander S. Sergeev: Section 9 of: Topological insulators and geometry of vector bundles, SciPost Physics Lecture Notes 67 (2023) [arXiv:2011.05004, doi:10.21468/SciPostPhysLectNotes.67]
See also:
- Wikipedia, Symmetry protected topological order
Review with focus on the case of topological insulators protected by crystallographic group-symmetry:
- Yoichi Ando, Liang Fu, Topological Crystalline Insulators and Topological Superconductors: From Concepts to Materials, Annual Review of Condensed Matter Physics 6 (2015) 361-381 [arXiv:1501.00531, doi:10.1146/annurev-conmatphys-031214-014501]
A proposal for classifying symmetry-protected topological order in terms of 2-groupoidal-actions on modular tensor categories:
-
Maissam Barkeshli, Parsa Bonderson, Meng Cheng, Zhenghan Wang, Symmetry Fractionalization, Defects, and Gauging of Topological Phases, Phys. Rev. B 100 115147 (2019) [arXiv:1410.4540, doi:10.1103/PhysRevB.100.115147, talk pdf]
-
Zhenghan Wang, §2.2 of: Beyond Anyons, Modern Physics Letters A 33 28 (2018) 1830011 [arXiv:1710.00464, doi:10.1142/S0217732318300112]
See also:
-
Chong Wang, T. Senthil, Interacting fermionic topological insulators/superconductors in three dimensions, Phys. Rev. B 89 195124 (2014) [arXiv:1401.1142, doi:10.1103/PhysRevB.89.195124
-
Hao Song, Sheng-Jie Huang, Liang Fu, Michael Hermele, Topological phases protected by point group symmetry, Phys. Rev. X 7 (2017) 011020 arXiv:1604.08151, doi:10.1103/PhysRevX.7.011020
-
Zhen Bi, Physical Properties and Experimental Platform of Symmetry Protected Topological Phases (2017) [escholarship:37q1k2rj]
Some of the above material is taken from:
Classification
Of free fermionic SPT phases
- Xiao-Gang Wen, Symmetry-protected topological phases in noninteracting fermion systems, Phys. Rev. B 85 (2012) 085103 doi:10.1103/PhysRevB.85.085103
Of bosonic and interacting SPT phases
Claim of classification of SPT phases via group cohomology:
-
Xie Chen, Zheng-Xin Liu, Xiao-Gang Wen, Two-dimensional symmetry-protected topological orders and their protected gapless edge excitations, Phys. Rev. B 84 (2011) 235141 doi:10.1103/PhysRevB.84.235141, arXiv:1106.4752
-
Xie Chen, Zheng-Cheng Gu, Zheng-Xin Liu, Xiao-Gang Wen, Symmetry protected topological orders and the group cohomology of their symmetry group, Phys. Rev. B 87 (2013) 155114 arXiv:1106.4772, doi:10.1103/PhysRevB.87.155114
-
Xie Chen, Zheng-Cheng Gu, Zheng-Xin Liu, Xiao-Gang Wen, Symmetry protected topological orders and the group cohomology of their symmetry group, Science 338 (2012) 1604-1606 (doi:10.1103/PhysRevB.87.155114)
-
Zheng-Cheng Gu, Xiao-Gang Wen, Symmetry-protected topological orders for interacting fermions – fermionic topological non-linear sigma-models and a group super-cohomology theory, Phys. Rev. B 90 115141 (2014) arXiv:1201.2648, doi:10.1103/PhysRevB.90.115141
Classification for free fermion SPT phases in twisted equivariant K-theory:
-
Alexei Kitaev, Periodic table for topological insulators and superconductors, Proc. L.D.Landau Memorial Conf. “Advances in Theor. Physics”, June 22-26, 2008, Chernogolovka, Russia, arxiv/0901.2686 (uses K-homology, Bott periodicity etc.)
-
Daniel S. Freed, Gregory W. Moore, Twisted equivariant matter, Annales Henri Poincaré December 2013, Volume 14, Issue 8, pp 1927–2023 arxiv/1208.5055 (uses equivariant K-theory)
For more on this see at K-theory classification of topological phases of matter
Proposal that the general classification involves 2-group-symmetries:
- Anton Kapustin, Ryan Thorngren, Higher symmetry and gapped phases of gauge theories, in Algebra, Geometry, and Physics in the 21st Century, Progress in Mathematics, 324 (2017) 177-202 [arXiv:1309.4721, doi:10.1007/978-3-319-59939-7_5]
Proposal that the general classification involves equivariant Whitehead-generalized cohomology theory:
- Charles Zhaoxi Xiong, Minimalist approach to the classification of symmetry protected topological phases, J. Phys. A: Math. Theor. 51 445001 (2018) doi:1701.00004, doi:10.1088/1751-8121/aae0b1
Examples
The 1d Haldane phase:
- Duncan Haldane, Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the nonlinear sigma model, Physics Letters A 93 9 (1983) 464-468 [doi:10.1016/0375-9601(83)90631-X]
Examples with braid group effects:
- Michael Levin, Zheng-Cheng Gu, Braiding statistics approach to symmetry-protected topological phases, Phys. Rev. B 86 (2012) 115109 (doi:10.1103/PhysRevB.86.115109)
and with loop braid group-effects:
- Chao-Ming Jian, Xiao-Liang Qi, Layer Construction of 3D Topological States and String Braiding Statistics, Phys. Rev. X 4 (2014) 041043 [doi:10.1103/PhysRevX.4.041043]
and with both:
- Zhen Bi, Yi-Zhuang You, Cenke Xu, Anyon and loop braiding statistics in field theories with a topological term, Phys. Rev. B 90 (2014) 081110(R) (doi:10.1103/PhysRevB.90.081110)
Other articles
-
Michael Levin, Zheng-Cheng Gu, Braiding statistics approach to symmetry-protected topological phases, Phys. Rev. B 86, 115109 (2012), arXiv:1202.3120.
-
Yuan-Ming Lu, Ashvin Vishwanath: Theory and classification of interacting integer topological phases in two dimensions: A Chern-Simons approach, Phys. Rev. B 86 (2012) 125119, Erratum Phys. Rev. B 89 (2014) 199903 [doi:10.1103/PhysRevB.86.125119, arXiv:1205.3156]
-
Davide Gaiotto, Theo Johnson-Freyd, Symmetry protected topological phases and generalized cohomology [arxiv/1712.07950]
-
Yizhi You, Trithep Devakul, F. J. Burnell, Titus Neupert, Higher order symmetry-protected topological states for interacting bosons and fermions, Phys. Rev. B 98 (2018) 235102 (arXiv:1807.09788v2, doi:10.1103/PhysRevB.98.235102)
-
Rongge Xu, Zhi-Hao Zhang, Categorical descriptions of 1-dimensional gapped phases with abelian onsite symmetries [arXiv:2205.09656]
Observation in experiment:
- Zhihuang Luo, Wenzhao Zhang, Xinfang Nie, Dawei Lu, Observation of a symmetry-protected topological phase in external magnetic fields [arXiv2208.05357]
Conference and seminar cycles
-
seminar in Koeln Topological states of matter
-
Topological Phases of Matter: Simons Center, June 10-14, 2013, videos available
-
Alexei Kitaev, On the classification of short-range entangled states, video
Last revised on July 18, 2025 at 19:21:11. See the history of this page for a list of all contributions to it.